Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

7.1 Concepts 231

the entire future spacetime is required to decide whether or not any particular null geodesic

will ultimately escape to inﬁnity. In numerical simulations an event horizon can be found

only “after the fact”, i.e., after the evolution has proceeded long enough to have settled

down to a stationary state.

Locating event horizons in “post-processing” may be sufﬁcient for diagnostic purposes,

i.e., for analyzing the geometrical and physical consequences of a black hole simulation

after it is completed, but it does not allow us to locate the black holes during the course of a

numerical simulation. The later can be important, and is sometimes essential, for allowing

the simulation to continue in the presence of one or more black holes. The spacetime

singularities inside the black holes must be excluded from the numerical grid, since they

would otherwise spoil the numerical calculation. Several of the following chapters treat

simulations in which black holes are present and there we will discuss several different

strategies for avoiding black hole singularities numerically. One approach is based on the

realization that, by deﬁnition, the interior of a black hole is causally disconnected from, and

hence can never inﬂuence, the exterior. This fact suggests that we may “excise”, i.e., remove

from the computational domain, the spacetime region inside the event horizon.

Black hole

“excision” requires at least approximate knowledge of the location of the horizon at all times

during the evolution, so the construction of the event horizon after the fact is not sufﬁcient.

The concept of apparent horizons allows us to locate black holes during the evolution.

The apparent horizon is deﬁned as the outermost smooth 2-surface, embedded in the spatial

slices , whose outgoing future null geodesics have zero expansion everywhere. We will

explain this notion in much greater detail in Section 7.3 below. As we will see, the apparent

horizon can be located on each slice , when it exists, and is therefore a local (in time)

concept. The singularity theorems of general relativity

tell us that if an apparent horizon

exists on a given time slice, it must be inside a black hole event horizon.

This theorem

makes it safe to excise the interior of an apparent horizon from a numerical domain.

Note, however, that absence of proof is not proof of absence: the absence of an apparent

horizon does not necessarily imply that a black hole is absent. One example can be found

in the Oppenheimer–Snyder collapse of spherical dust to a black hole as constructed in

Chapter 1.4; we will return to this example in Section 7.3.1. It is also possible to construct

slicings of the Schwarzschild geometry in which no apparent horizon exists.

Also, it is

straightforward to show that apparent horizons do not form during spherical collapse in

polar slicing.

These examples demonstrate the gauge-dependent nature of the apparent horizon. Nev-

ertheless, the usual expectation when performing a black hole a simulation is that, except

Unruh (1984), as quoted in Thornburg (1987); see also Chapters 13.1.1 and 14.2.3.

See Hawking and Ellis (1973); Wald (1984) for an introduction.

This statement is not necessarily true in other theories of gravity. In Brans–Dicke theory, for example, apparent horizons

may exist outside of event horizons; see Scheel et al. (1995b) for a numerical example.

Wald and Iyer (1991)

See exercises 7.13 and 8.10.

232 Chapter 7 Locating black hole horizons

when choosing a special slicing in which an apparent horizon is known to be absent, an

apparent horizon will eventually appear on the slice whenever a black hole is present.

The fact that the apparent and event horizons always coincide in a stationary spacetime

promotes this expectation.

Now consider constructing the worldtube H formed by stacking together apparent

horizons on different spatial slices . In general, H can make discrete jumps and does

not need to be continuous (see Chapter 1.4 and Figure 1.3). When matter or radiation

falls into the black hole the horizon H expands. When the black hole is isolated, however,

and absorbs no more matter or radiation, H becomes a null-surface. In this regime H

can be described within the isolated horizon framework.

Using information on H , this

formalism provides a coordinate-independent deﬁnition of the black hole mass and angular

momentum, as we will discuss below.

7.2 Event horizons

Event horizons are spanned by outgoing light rays that neither reach future null inﬁnity

nor hit the black hole singularity. As a nontrivial but analytical example, we located

the event horizon in the Oppenheimer–Snyder collapse of a dust sphere to a black hole

in Chapter 1.4. In principle, knowledge of the entire future evolution of a spacetime is

necessary to determine the fate of outgoing light rays and thereby locate event horizons. In

practice, however, event horizons can be identiﬁed fairly accurately after a ﬁnite evolution

time in a numerical simulation, provided the spacetime has settled down to a nearly

stationary state.

An obvious approach to locating an event horizon in this situation is to evolve null

geodesics,

whose worldlines are governed by the equation

dλ

(4)



dλ

= 0, (7.5)

where λ is an afﬁne parameter. Splitting this second-order equation into two ﬁrst-order

equations and substituting 3 + 1 metric quantities yields

dλ

=−α∂

α( p

)

+ ∂

−

∂

dλ

= γ

− β

(7.6)

wherewehaveused p

= dx

/dλ and p

= (γ

)

1/2

/α (which enforces g

0).

Exercise 7.3 Derive equations (7.6).

In a numerical spacetime, the lapse α, the shift β

and the spatial metric γ

are known

on the computational grid, so that light rays can be ejected in different directions p

from

Ashtekar et al. (2000); Ashtekar and Krishnan (2004).

See, e.g., Hughes et al. (1994).

7.2 Event horizons 233

every point x

in spacetime and their geodesic trajectories tracked. The search for an event

horizon can be expedited by knowing the location of the apparent horizons. If all light rays

sent out from an event x

end up inside an apparent horizon (which is always located inside

an event horizon) the event must reside inside the event horizon as well. If, on the other

hand, at least one light ray sent out from the event escapes to large separations, it is not

inside an event horizon. By distinguishing events in this way, the ejection and propagation

of light rays from various points in spacetime can delineate the location of the event

horizon.

In practice it is more expeditious to integrate null geodesics backwards in time.

Future

directed light rays diverge away from the event horizon, either toward the interior of

the black hole or toward future null inﬁnity. By contrast, backwards propagating rays

converge on the event horizon, which thus acts as an “attractor” for these rays. This

method is particularly efﬁcient if one can identify a ﬁnite region in spacetime within

which the event horizon is expected to reside. It is then sufﬁcient to integrate light rays

from events residing in this region at late times, and they will be attracted to the event

horizon.

This method becomes quite transparent in spherical symmetry, where we can often

ﬁnd the trajectories of “outgoing” null geodesics analytically. The label “outgoing” is

somewhat misleading, since inside the event horizon all worldlines propagate to smaller

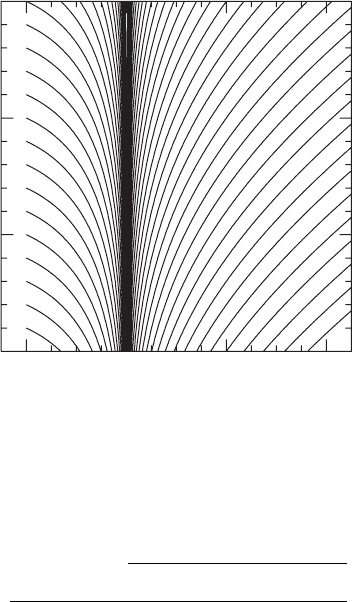
areal radius. For example, for a Schwarzschild black hole in Kerr–Schild coordinates, we

noted in exercise 6.3 that outgoing null geodesics must satisfy

t − r = 4M ln |r/2M − 1|+constant. (7.7)

As shown in Figure 7.1, tracing these geodesics backwards in time inevitably brings us to

the event horizon at r = 2M.

In nontrivial applications, this technique has been used to probe the topology of the

event horizon arising during the head-on collision and merger of two black holes, as well

as the collapse of a rotating toroidal cluster to a toroidal black hole. The “pair of pants”

that the event horizon forms in a spacetime diagram for the collapse of two collisionless

clusters to two black holes, followed by their head-on collision, is depicted in Figure 10.5.

We postpone a discussion of these simulations until Chapter 10.2 and 10.4.

Instead of integrating individual null geodesics, we can also consider constructing a

2 + 1 dimensional null hypersurface enclosing a bundle of outgoing null geodesics in

spacetime.

We can deﬁne such a null hypersurface as a level surface of some function

f (t, x

), say f (t, x

) = 0. Given that the normal vector ∂

f to such a null hypersurface

must itself be null,

the function f must satisfy

∂

f ∂

f = 0. (7.8)

See Hughes et al. (1994); Anninos et al. (1995); Libson et al. (1996).

See Anninos et al. (1995); Libson et al. (1996).

See, e.g., Wald (1984), p. 65.

234 Chapter 7 Locating black hole horizons

246

r/M

t/M

Figure 7.1 Worldlines of outgoing null geodesics in a Schwarzschild spacetime in Kerr–Schild coordinates (see

exercise 6.3). Traced backwards in time, these rays are strongly attracted to the event horizon at r/M = 2. These

worldlines coincide with contours of the function f introduced in equation (7.8).

Solving for ∂

f we then ﬁnd an evolution equation for f ,

∂

f =

−g

∂

f +



∂

f )

− g

∂

f ∂

, (7.9)

where we have chosen the positive root so that the surface is generated by outgoing null

geodesics. Expressing the spacetime metric in terms of the lapse, shift and spatial metric

we ﬁnd

∂

f = β

∂

f −



∂

f ∂



1/2

. (7.10)

Exercise 7.4 Derive equation (7.10) from (7.8).

It is particularly easy to use equation (7.10) to locate an event horizon if, at late time,

we can bracket it by two null hypersurfaces, e.g., S

and S

. Suppose each one of these two

hypersurfaces is deﬁned by a certain value, say zero, of two functions f

and f

. Knowing

the location of the apparent horizon at late times again facilitates the choice of S

and S

We can use equation (7.10)toevolve f

and f

backwards in time, and ﬁnd S

and S

earlier times by locating f

= 0and f

= 0. The two hypersurfaces will converge on the

event horizon.

In spherical symmetry it is easy to ﬁnd the general solution for f , which illustrates why

this approach works. By construction, f is constant along outgoing light rays. In Kerr–

Schild coordinates, outgoing light rays travel along the characteristics (7.7). Any arbitrary

7.3 Apparent horizons 235

Figure 7.2 The “pair of pants” formed by the event horizon in a spacetime diagram depicting the head-on

collision of two “eternal” black holes. [From Matzner et al. (1995).]

function

f = f (t − r − 4M ln |r/2M − 1|) (7.11)

must therefore be a solution to equation (7.10).

Exercise 7.5 Verify that any function f = f (t −r − 4M ln |r/2M − 1|) is a solu-

tion to equation (7.10).

This technique has been used to construct the event horizon for yet another scenario

describing the head-on collision of two black holes. We will also discuss this scenario,

which involves “eternal” black holes, in Chapter 10.2, but here, in anticipation, we show a

spacetime diagram depicting the event horizon in Figure 7.2.

7.3 Apparent horizons

Consider a smooth, closed, 2-dimensional hypersurface S residing in . By construction, S

is spatial. Let s

be its outward pointing unit normal lying in . Evidently s

then satisﬁes

= 1ands

= 0. Just as the spacetime metric g

induces the spatial metric γ

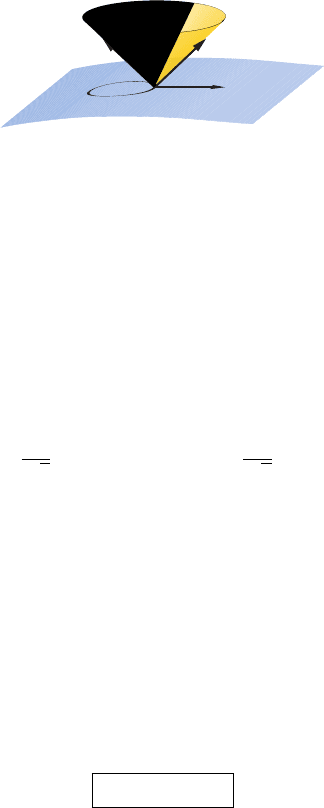
236 Chapter 7 Locating black hole horizons

Figure 7.3 A smooth, 2-dimensional, hypersurface S is embedded in . The unit, outward-pointing normal to S

lying in  is s

, and the normal to  is n

. The outgoing and ingoing null tangent vectors k

and l

are

constructed as linear combinations of n

and s

 (see Chapter 2.3), the metric γ

induces a 2-dimensional metric m

on S given by

= γ

− s

= g

+ n

− s

. (7.12)

For each point on S we can now construct a pair of future-pointing null geodesics whose

projection on  is orthogonal to S. Up to an overall factor, the tangents k

and l

to these

geodesics on S are

≡

√

+ s

)andl

≡

√

− s

) (7.13)

(see Figure 7.3). By construction we have k

= 0andm

= 0aswellasl

= 0

and m

= 0, and we have chosen the normalization so that k

=−1. We call k

the

tangent to the “outgoing” and l

the tangent to the “ingoing” null geodesic. These names

are again somewhat misleading, since inside a black hole both tangents point toward the

black hole’s interior. Combining equations (7.12) and (7.13) we can express m

in terms

of k

and l

= g

+ k

. (7.14)

The expansion of the outgoing null geodesics orthogonal to S is

 = m

∇

. (7.15)

Note that k

is only deﬁned on S. The projection with m

ensures that only derivatives

tangent to S enter this expression, so that no knowledge of k

away from S is required in

this deﬁnition of the expansion.

Exercise 7.6 Show that the deﬁnition (7.15) is equivalent to

 =∇

(7.16)

if we assume that the null tangent vectors k

are afﬁnely parametrized, i.e., k

∇

0, in a neighborhood of S.

We now deﬁne an outer-trapped surface as a 2-dimensional surface S embedded in

 on which the expansion  of the outgoing null geodesics orthogonal to S is negative

7.3 Apparent horizons 237

everywhere.

We further deﬁne a trapped region as any region of  that contains outer-

trapped surfaces.

Finally, we deﬁne the apparent horizon as the outer boundary of any

connected trapped region. This deﬁnition makes the apparent horizon a marginally outer-

trapped surface on which the expansion of outgoing null geodesics vanishes

 = 0. (7.17)

Before proceeding with the formal derivation it may be useful to illustrate the above

concepts with a simple example in spherical symmetry. Without loss of generality we can

write the spacetime line element in spherical polar coordinates in the form

=−(α

− A

)dt

+ 2A

βdrdt + A

+ B

(dθ

+ sin

θdφ

). (7.18)

The only nonvanishing component of the shift vector β

is the radial component, which

we call β, and we may further assume that α, β, A and B are functions of t and r only.

Consider a spherical surface S centered on the origin. The spatial normal vector s

to S

must then be radial and take the form

= (0, A

−1

, 0, 0) (7.19)

and hence s

= (Aβ, A, 0, 0). We can now construct the outgoing null normal

√

(Aβ − α, A, 0, 0) and k

√

(α

−1

, A

−1

− α

−1

β, 0, 0), (7.20)

as well as the induced metric on S

= diag(0, 0, B

, B

sin

θ). (7.21)

Computing the expansion  we ﬁnd

 =

√



∂

(Br) +



−



∂

(Br)



. (7.22)

Exercise 7.7 Derive equation (7.22).

So far this result is not too enlightening. It turns out, however, that the expression in

parentheses is proportional to the rate of change of the areal radius along k

. The areal

radius is R

area

= Br, and its directional derivative along k

is therefore

∇

area

= k

∂

(Br) + k

∂

(Br) =

√



∂

(Br) +



−



∂

(Br)



. (7.23)

E.g. Hawking and Ellis (1973); Wald (1984).

Some authors deﬁne a trapped region in terms of trapped surfaces as opposed to outer-trapped surfaces. For trapped

surfaces the expansion of the ingoing null geodesics orthogonal to S is required to be negative, 

(l)

< 0, in addition

to <0. For the purposes of this section this distinction is unimportant.

238 Chapter 7 Locating black hole horizons

Combining equations (7.22) and (7.23)wehave

 =

area

∇

area

4π R

area

∇

(4π R

area

). (7.24)

Equation 7.24 shows that the expansion  measures the fractional change of the cross-

sectional area of a bundle of outgoing null rays with tangent vectors k

, or, equivalently,

the fractional change in the area of an outward spherical ﬂash of light.

Exercise 7.8 Show that

 =

1/2

= L

ln m

1/2

, (7.25)

where m is the determinant of the induced metric m

.Sincem

1/2

x is the proper

area element of a cross-section of a bundle of null rays k

, it can then be shown that

 measures its fractional change of cross-sectional area in general, and not only in

spherical symmetry.

With this result the deﬁnition of an apparent horizon becomes very simple to apply in

spherical symmetry. The area

A of a spherical ﬂash of light rays emitted radially outward

will propagate instantly to a larger area if it is emitted outside an apparent horizon, to a

smaller area if emitted inside an apparent horizon, and remain constant if emitted on the

apparent horizon.

Consider, for example, a Schwarzschild black hole in isotropic coordinates (see, e.g.,

Table 2.1), for which A = B = ψ

= (1 + M/(2r))

, β = 0, and ∂

(Br) = 0. According

to equation (7.22) the expansion  then vanishes when ∂

(Br) = 0, which occurs at

r =

. (7.26)

In exercise 3.4 we have seen that this isotropic radius corresponds to an areal radius of

areal

= 2M. Not surprisingly, the apparent horizon coincides with the event horizon in

this static spacetime.

Exercise 7.9 Verify that for a Schwarzschild black hole in Schwarzschild, Kerr–

Schild and Painlev

e–Gullstrand coordinates the apparent horizon is located at

areal

= 2M.

Returning to our general derivation, we would like to bring the expansion (7.15)intoa

form that is more suitable for evaluation in a 3 + 1 numerical simulation and write it in

terms of 3-dimensional spatial objects. Substituting equation (7.13)into(7.15)wehave

√

2 m

∇

= m

∇

+ s

) = m

− K

) (7.27)

or, using equation (7.12)inm

, we obtain

√

2 m

∇

= D

− K + s

. (7.28)

See also the discussion in Poisson (2004), Section 2.4.

7.3 Apparent horizons 239

Here we also have used the relation s

= 1 as well as the deﬁnition (2.49) of the extrinsic

curvature. The apparent horizon condition is therefore

0 =

√

2  = m

− K

) (7.29)

or equivalently

0 =

√

2  = D

− K + s

. (7.30)

Exercise 7.10 Show that with the conformal rescalings (3.5), (3.35)ands

= ψ

−2

the apparent horizon condition (7.30) can be written as

+ 4

ln ψ −

K + ψ

−4

= 0. (7.31)

It is often useful in the search for apparent horizons to characterize the horizon as a level

surface of a scalar function, e.g.,

τ (x

) = 0. (7.32)

We can then write the unit normal s

= λD

τ, or s

= λD

τ = λ∂

τ, (7.33)

where λ is the normalization factor

λ ≡



τ D



−1/2

. (7.34)

In the expression

(λD

τ ) = m

λD

τ + m

λ)(D

τ ) (7.35)

the second term vanishes, since D

τ is proportional to s

, which vanishes when contracted

with m

. Substituting equation (7.33)into(7.29) therefore yields

0 = m

(λD

τ − K

) = m

(λ∂

∂

τ − s



− K

). (7.36)

A particularly useful form of the level function τ is

τ (x

) = r

) − h(θ,φ), (7.37)

where r

is the coordinate separation between the point x

and some ﬁducial point C

inside the τ = 0 surface, and where θ and φ are spherical polar coordinates centered on

. In the following we will assume that C

is the origin of the coordinate system, so

that C

= 0, but the generalization to a point that does not coincide with the origin is

straightforward. The function h then measures the coordinate distance from the origin to

the τ = 0 surface in the (θ,φ) direction.

The ﬁrst derivative of equation (7.37)is

∂

τ = σ

− ∂

h, (7.38)

240 Chapter 7 Locating black hole horizons

where σ

≡ ∂

is the unit vector in the (θ,φ) direction. In spherical polar coordinates r

is simply r , so that σ

= (1, 0, 0). Since ∂

= 0, the apparent horizon condition (7.36)

reduces to

0 =

√

2 = m

(λ∂

∂

h − s



− K

) (spherical polar coordinates). (7.39)

Exercise 7.11 Show that in Cartesian coordinates the apparent horizon condition

(7.36) becomes

0 =

√

2 = m



(δ

− σ

) + λ∂

∂

h − s



− K



(Cartesian coordinates).

(7.40)

We have now expressed the apparent horizon condition as a second-order partial differ-

ential equation for the function h that measures the horizon’s coordinate distance from the

origin. The principal part of the equation, m

∂

h, involves a Laplacian with respect to

the 2-dimensional metric m

on the surface S. Finding solutions to these elliptic equations,

and hence locating apparent horizons, is in general not at all a trivial matter, in particular

since the normal vector s

also contains derivatives of h. For the remainder of this section

we will discuss strategies for locating apparent horizons on spatial hypersurfaces exhibiting

spherical symmetry, axisymmetry, and without any special symmetry.

7.3.1 Spherical symmetry

In spherical symmetry h is a constant and does not depend on θ or φ. The second deriva-

tives in the differential equation (7.39) therefore vanish, and s

= λσ

can be constructed

algebraically from the metric. The expansion  then reduces to the algebraic expression

 =−

√



+ K

) (7.41)

which only depends on radius r. Finding an apparent horizon simply amounts to ﬁnding a

root of this function. This simpliﬁcation does not come as a surprise, of course, since we

have seen before that apparent horizons can be located quite easily in spherical symmetry.

Exercise 7.12 Verify that for a metric of the form (7.18) the expansion (7.41) yields

(7.22).

Exercise 7.13 (a) Show that in spherical symmetry and isotropic coordinates

(i.e., A = B in the metric 7.18) the apparent horizon condition reduces to

1 + r

∂

−

= 0, (7.42)

where K

is deﬁned by equation (4.63).

(b) Use equation (7.42) to argue that apparent horizons do not form in polar slicing,

provided dr

/dr = 0, where r is the isotropic radius and r

is the areal radius.