Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

8.1 Black holes 261

We have now assembled the basic equations and are ready to integrate them to obtain

the solution. Note that in spherical symmetry, which contains no dynamical degrees of

freedom (i.e., no gravitational waves), it is not necessary to solve an evolution equation

either for the 3-metric variable A or the extrinsic curvature variable K

. These longitudinal

quantities are determined on any time slice entirely by the Hamiltonian and momentum

constraint equations. For example, we may solve the constraint equation (8.22)forA in

lieu of the evolution equation (8.21). For this reason we say that in spherical symmetry the

gravitational ﬁeld evolution is completely constrained.

Equation (8.24) immediately gives

β = α AT/r

, (8.27)

where T = T (

t) is a constant of integration that can be a function of

t only. Substituting

this result into equation (8.23) and integrating yields

A =

1 − 2M/r + T

, (8.28)

where the new constant of integration M is again a function of

t only. By going to large

r we we will be able to identify M with the total mass-energy of the black hole, once

we show that it is independent of

t. Taking a time derivative of equation (8.28) and using

equations (8.21) and (8.27) yields

∂

(α A

1/2

) = A

3/2

(r∂

M/T − ∂

T/r

), (8.29)

which we will integrate for the lapse shortly. Substituting equation (8.27) into equation

(8.26), and using the time derivative of equation (8.28) to help evaluate the left-hand side

shows, after some algebra, that ∂

M = 0, hence M is constant, as anticipated. We now

integrate equation (8.29) to get the lapse function, using equation (8.28) and the condition

that α → 1asr →∞:

α = (1 − 2M/r + T

)

1/2

1 +

∂



M/r

dx (1 −2x + T

)

−3/2

. (8.30)

Using equations (8.23) and (8.27) one can check that equation (8.25),whichwehavenot

needed to solve for the lapse, is automatically satisﬁed by equation (8.30).

So far, the constant of integration T = T (

t) is undetermined. We can now pick out a

particular maximal slicing of Schwarzschild by determining this function. Setting T = 0,

for example, we recover the familiar t

= constant slices, for which equations (8.28)and

(8.30) reduce to equations (8.3) and (8.2) with zero shift.

Exercise 8.3 Check that the static Schwarzschild metric (8.3)and(8.2) satisﬁes

equation (8.25).

If we set T to a constant, say T = C, we recover the family of time-independent maximal

slicings of Schwarzschild, equations (4.23)–(4.25), that we derived in Chapter 4.2 with the

262 Chapter 8 Spherically symmetric spacetimes

help of an alternative “height-function” approach. Evidently, there exist many different

maximal slices of Schwarzschild.

How is it possible that the same maximal slicing condition for the lapse, equation (8.25),

a second-order partial differential equation, is satisﬁed for different solutions? The answer

lies in the different inner boundary condition imposed on the lapse on the black hole throat.

Setting α = 0 on the Einstein–Rosen bridge at the center of the throat leads to standard

static time slicing with T = 0. By contrast, setting ∂

α = 0 to require “smoothness” across

the throat, results in a dynamical time slicing solution, the derivation of which we have

nearly completed. In obtaining equation (8.30) for the lapse by integrating equation (8.29)

rather than by integrating equation (8.25), we simply postponed having to specify inner

boundary conditions on the throat.

The dynamical maximal time-slicing solution for the spacetime is given by equa-

tions (8.27), (8.28) and (8.30). However, there still remains one unknown in these equations:

the function T and its dependence on

t. Specifying this function will now require that we

explicitly impose an inner boundary condition on the black hole throat, and, as mentioned

above, we shall impose “smoothness” across the throat to get the desired solution. The

simplest way to do this is to transform to standard Schwarzschild coordinates, (t, r,θ,φ),

where t = t(

t, r) but where the spatial coordinates are the same. Matching the line ele-

ment (8.13) with the standard Schwarzschild line element gives

∂

t = α A

1/2

, (8.31)

∂

t = A

1/2



(2M/r − 1)



. (8.32)

Exercise 8.4 Verify equations (8.31)and(8.32).

Integrating equation (8.32) yields

t/M = (T /M

)



X(T )

M/r

dx(1 − 2x + T

)

−1/2

(2x − 1)

−1

, (8.33)

where X (T ) is determined by differentiating equation (8.33) with respect to

t, substituting

into equation (8.31), and using equation (8.30)toget

= T

−1

(2X − 1)(1 −2X + T

)

1/2

∂



dx(1 − 2x + T

)

−3/2

(8.34)

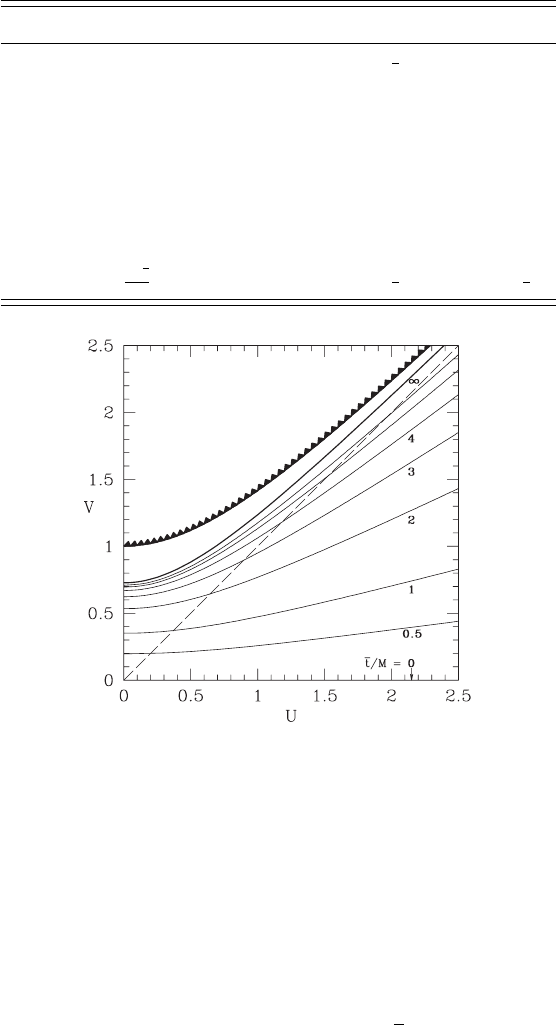
Now we can impose the “smoothness” requirement at the center of the Einstein–Rosen

bridge along t = 0forr < 2M (i.e., along u = 0,v > 0, in Kruskal–Szekeres coordinates).

Smoothness requires that, when viewed in a Kruskal–Szekeres diagram, each

t = constant

slice intersect the center of the bridge in the normal direction, so that as t → 0, we have that

∂

t →∞as r approaches its minimum value r

min

= r

min

(

t) along the slice (see Figure 8.3).

Demanding that this condition be satisﬁed by equations (8.32) and (8.34) requires that r

min

be equal to M/ X (T ) for that value of X (T ) that is the smaller of the two real roots of the

8.1 Black holes 263

Table 8.1 Parameters on selected maximal slices.

t/MT/M

∂

T/MXr

min

001

1 0.8104 0.5350 0.5249 1.9050

2 1.1384 0.1791 0.5670 1.7638

3 1.2460 0.0585 0.6019 1.6615

4 1.2814 0.0193 0.6263 1.5965

5 1.2931 0.0065 0.6422 1.5570

6 1.2970 0.0022 0.6521 1.5334

7 1.2984 0.0007 0.6581 1.5195

8 1.2988 0.0002 0.6617 1.5114

∞

√

Figure 8.3 Maximal time slices of a Schwarzschild black hole, plotted on a Kruskal–Szekeres diagram. The

dashed line denotes the event horizon at r

/M = 2, the sawtooth curve denotes the central singularity at

/M = 0 and the darker solid line shows the limiting slice at r

= 3M/2.

fourth-order polynomial equation 1 − 2x + T

= 0. It turns out that equation (8.34)

is automatically satisﬁed when X (T ) is a root of this polynomial.

We now can get the desired relation between T and

t. Setting

t = t at r =∞in

equation (8.33)gives

t/M = (T /M

)



X(T )

dx(1 − 2x + T

)

−1/2

(2x − 1)

−1

. (8.35)

For each allowed value of T , where 0 ≤ T/M

≤ 3

√

3/4, the polynomial equation

determines X(T ) and equation (8.35) gives the value of

t parametrizing the maximal

hypersurface. Values of key parameters on select hypersurfaces are listed in Table 8.1.It

264 Chapter 8 Spherically symmetric spacetimes

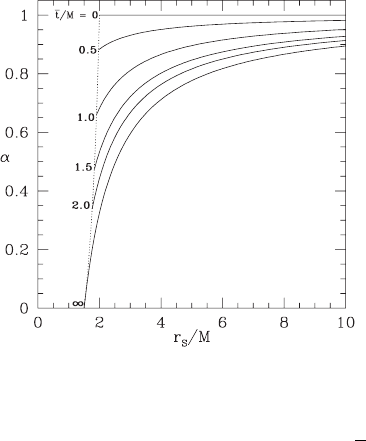
Figure 8.4 The lapse α as a function of areal radius r

on selected maximal slices.

is relevant to note that the integral in equation (8.35) diverges when the two real roots of

the fourth-order polynomial coincide. This occurs at T/M

= 3

√

3/4, for which one ﬁnds

t =∞, X = 2/3, r

min

/M = 3/2andα = 0. Thus the foliation of the black hole spacetime

terminates at this limit slice, beyond which maximal slicing cannot probe. Encountering

a limit slice is a characteristic of maximal time slicing and even occurs in nonvacuum

scenarios when using maximal slicing to follow the collapse of a star or star cluster to a

black hole. Given that all of the slices, including the limit slice, avoid hitting the central

singularity, while all events in the domain of outer communications are covered, such a

foliation of the black hole spacetime is “good news” from a numerical point of view.

Otherwise, a simulation designed to build the spacetime numerically would terminate

due to computer overﬂows upon encountering the central singularity. In this situation the

numerical evolution would come to an abrupt end, even if one were interested only in the

black hole exterior.

In Figures 8.4–8.6 we plot the proﬁles of α, β and A on selected maximal hypersurfaces.

The “collapse of the lapse” near the center of the Einstein–Rosen bridge inside r = 2M

that we expect with maximal slicing at late times

is evident in Figure 8.4. The “bad news”

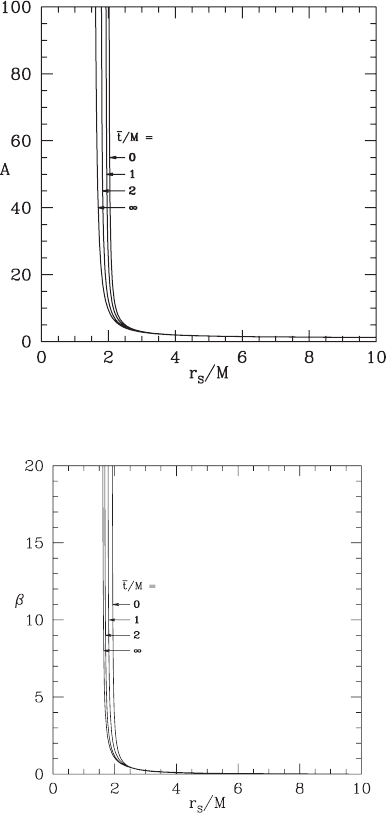
from a numerical standpoint is that metric functions like A blow up at the center of the

bridge at r

min

. The metric coefﬁcients in Kerr–Schild slicing, discussed in the previous

section, do not blow up on the slice until reaching the central singularity (cf. equation 8.7).

However, Kerr–Schild slices do hit the central singularity, which would be disastorous in a

numerical simulation. So a better solution to constructing the spacetime numerically would

be to eliminate at least part of the black hole interior – after all, the black hole exterior

However there do exist cases, e.g., extremely inhomogeneous dust balls, for which maximal slicing fails, hitting the

central singularity before covering the domain of outer communications of the resulting black hole; Eardley and Smarr

(1979).

Recall our discussion in Chapter 4.2.

8.1 Black holes 265

Figure 8.5 The radial metric coefﬁcient A(= γ

) as a function of areal radius r

on selected maximal slices.

Figure 8.6 The radial shift β as a function of areal radius r

on selected maximal slices.

cannot be affected by the interior, so there should be no need to compute the interior.

This black hole excision technique

does not rely on any particular slicing condition in the

exterior, and can be used as long as the grid functions remain sufﬁciently well-behaved

outside the excision surface. We will discuss some examples in Chapters 13 and 14.An

alternative approach might use the moving-puncture approach,

which adopts a particularly

well suited set of coordinates that avoids the spacetime singularities without developing the

See Chapters 13.1.2 and 14.2.3.

See Chapter 13.1.3.

266 Chapter 8 Spherically symmetric spacetimes

pathologies described above. Examples of moving-puncture simulations will be described

in Chapters 13 and 17.

8.2 Collisionless clusters: stability and collapse

Collisionless particles provide a convenient matter source for developing numerical relativ-

ity algorithms in general, and for problems involving relativistic matter in particular. By the

same token, numerical relativity provides a powerful tool for studying the physical behav-

ior and astrophysical implications of self-gravitating clusters of relativistic, collisionless

particles.

From a technical point of view, working with collisionless matter has some advantages

over ﬂuid systems for designing and testing numerical relativity schemes. The collisionless

matter equations can be represented as ordinary differential equations (geodesic equations;

recall Chapter 5.3 and equation 5.222) and thus are straightforward to integrate, while

hydrodynamical equations are partial differential equations and require more subtle han-

dling. Furthermore, collisionless matter is not subject to shocks or other discontinuities

that often require special treatment, or sophisticated schemes, in numerical simulations to

give reliable results.

Numerical relativity simulations have resolved a number of longstanding issues in rela-

tivistic stellar dynamics, issues which had been unresolved even for spherically symmetric

systems. These results have far wider applicability than stellar dynamics, in that the matter

ﬁelds need not be identiﬁed with stars per se but with any gas of self-gravitating, colli-

sionless particles, as emphasized in Chapter 5.3. As an example of such an issue, consider

that, in contrast to the situation for spherical ﬂuid stars in general relativity, there exists

only sufﬁcient, but not necessary, criteria for the dynamical radial stability of a spherical

collisionless cluster. Speciﬁcally, linear perturbation theory, using trial functions in a vari-

ational principle, had demonstrated that along a one-parameter sequence of equilibrium

clusters parametrized by z

, the central redshift of the conﬁguration, the onset of instability

occurs near the point of maximum fractional binding energy (E

≡ (M

− M)/M

,where

M is the total mass-energy and M

is the rest-mass), independent of the nature of the

equilibrium models.

In typical models a turning point in the relativistic binding energy

curve occurs at high redshift, z

≈ 0.5. Subsequently, a theorem was then proven rigorizing

this result, but it is restricted, stating only that that the equilibrium conﬁgurations are stable

at least up to the ﬁrst maximum of the fractional binding energy along the sequence.

This contrasts with the situation for a spherical ﬂuid equilibria (stars) in general relativity,

for which the binding energy maximum, equivalent to the “turning point” along the M

vs. ρ

curve(seeChapter1.3), identiﬁes precisely the onset of radial instability. Fully

nonlinear, time-dependent simulations furnish strong numerical evidence that the turning

point in the binding energy curve does in fact signal the the onset of dynamical radial

Ipser and Thorne (1968); Ipser (1969a,b); Fackerell (1970).

Ipser (1980).

8.2 Collisionless clusters: stability and collapse 267

instability along an equilibrium sequence of collisionless clusters. Numerical relativity has

thus “discovered” a theorem awaiting a formal proof.

By far the most interesting and important results to emerge from the numerical simula-

tions deal with the nonlinear evolution and ﬁnal fate of unstable clusters. They corroborate

earlier speculation

that unstable clusters inevitably undergo catastrophic collapse to

black holes. They also demonstrate that when the nearly homogeneous core of a centrally

concentrated (“core-halo”) cluster undergoes collapse, a mass much larger than the core

ultimately forms the central black hole. This occurs because of the so-called “avalanche

effect”, whereby the black hole formed from the collapse of the initial core grows by

capture of lower-angular momentum stars that orbit at increasingly larger apocenter from

the center but wander close to the hole at pericenter. At the end of the collapse, the clus-

ter settles into a new stationary state consisting of a massive, nearly Newtonian halo in

orbit about a central black hole. This numerical example provides one viable scenario for

forming a supermassive black hole.

Relativistic “violent relaxation”, or “dynamical phase mixing”, has also been explored

by simulations. In violent relaxation, collective ﬂuctuations in the time-varying gravita-

tional ﬁeld lead to particle thermalization.

In general relativity, a bound, nonequilibrium

collisionless cluster can either achieve virial equilibrium via violent relaxation or else

collapse to a black hole.

In the sections that follow we will sketch exactly how some of the numerical calculations

of collisionless clusters have been performed. The key computational challenge involves

black hole formation and singularity avoidance in cases of catastrophic cluster collapse.

We will focus on a few of the ways that this challenge has been overcome successfully.

8.2.1 Particle method

Physical picture

Consider any spherical surface drawn in the interior of a spherical distribution of particles

(see Figure 8.7). The surface is densely and uniformly covered with an inﬁnite number

of particles, each with an inﬁnitesimal rest mass. Particles move both in the radial and

transverse directions, but to preserve spherical symmetry, their transverse motion must be

isotropic. Accordingly, even as individual particles may have nonzero angular momentum

about the cluster center, the total angular momentum summed over all the particles is

strictly zero.

The restriction to spherical symmetry reduces the number of degrees of freedom in phase

space that we need to consider. In coordinate space the only nontrivial dynamical variable

For numerical simulations in spherical symmetry, see Shapiro and Teukolsky (1985b,a,c, 1986) and, for a review and

references, Shapiro and Teukolsky (1992a). The discussion in this section is drawn from the later two references and

Rasio et al. (1989b). See also Olabarrieta and Choptuik (2002).

Zel’dovich and Podurets (1965); see also Fackerell et al. (1969).

This was ﬁrst discussed in Newtonian gravitation by Lynden-Bell (1967). See also Binney and Tremaine (1987)for

discussion.

268 Chapter 8 Spherically symmetric spacetimes

Figure 8.7 Schematic representation of the distribution of particles in a spherical cluster (see text). [After

Shapiro and Teukolsky (1992a).]

is the radius r of a particle. In velocity space the only nontrivial dynamical variables are

the radial and transverse velocities, u

and u

⊥

Newtonian limit

Prior to describing the relativistic problem, it is useful to consider how a spherical cluster

of collisionless particles can be evolved in Newtonian physics. In this limit, the metric

reduces to

=−(1 + 2)dt

+ dr

d

, (8.36)

where  is the Newtonian potential. The particles move according to the geodesic equation,

which is simply Newton’s law of motion,

= u

=−∇, (8.37)

where x

and u

are the position and velocity 3-vectors of each particle. In spherical

symmetry these equations simplify to

= u

=−∂

 +

, (8.38)

= 0 (orbit conﬁned to the plane θ =

= 0 (conservation of angular momentum).

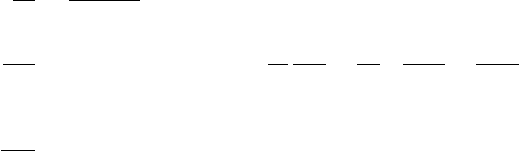
8.2 Collisionless clusters: stability and collapse 269

These equations are integrated forward in time for every particle for a small time step. The

new particle positions yield the rest-mass density ρ at the new time:

ρ =



all particles

mn, (8.39)

where m is the particle rest mass and n is the number density. The rest-mass density serves

as the (only) source term for the gravitational ﬁeld equation, which in this case is just

Poisson’s equation,

∇

 = 4πρ. (8.40)

Solving this equation gives the self-consistent gravitational ﬁeld at the new time. The new

potential is then inserted in the particle equations of motion and the process is repeated

for another time step. This approach to evolving a self-gravitating, collisionless N -body

system is known as a mean-ﬁeld, particle simulation scheme, and is well studied in the

Newtonian domain.

The general relativistic formulation

A mean-ﬁeld, particle simulation scheme for general relativity can be constructed in a

similar fashion to the Newtonian scheme described in the previous section, as shown by

Shapiro and Teukolsky (1985b,a,c, 1986, 1992b). The matter is evolved by N -body particle

simulation and provides the source for the mean gravitational ﬁeld, or metric. The metric

is determined by solving the standard 3 + 1 (ADM) equations.

For a spherical spacetime, we shall adopt the metric in isotropic form,

=−(α

− A

)dt

+ 2A

βdrdt + A

(dr

dθ

sin

θdφ

). (8.41)

Here we have set β = β

, the contravariant radial component of the shift vector, the only

nonvanishing component.

The stress-energy tensor for the matter is given by equation (5.221) and the equa-

tions of motion (∇

= 0) are the geodesic equations for each particle, given by

equations (5.223) and (5.224), with normalization condition (5.225). As in Newtonian

gravitation, these equations simplify considerably in spherical symmetry, yielding

αu

(αu

)

− β,

=−(αu

)∂

α + u

∂

β +

∂



∂



, (8.42)

= 0,

= 0.

270 Chapter 8 Spherically symmetric spacetimes

The normalization condition u

=−1gives

αu



1 +



1/2

. (8.43)

Exercise 8.5 Verify equations (8.42)and(8.43). Show that they reduce to equa-

tions (8.38) in the Newtonian limit, where A → 1, α → 1, ∂

α → ∂

, β → 0and

αu

→ 1.

Hence, given the metric at any time t, equations (8.42) and (8.43) are integrated forward

in time for the new particle positions and 4-velocities at t + t.

Given the particle positions and velocities, the matter source terms appearing in the ﬁeld

equations can be calculated according to equations (5.226)–(5.229). For spherical systems,

they yield

ρ =



, (8.44)



, (8.45)



, (8.46)

S = ρ −



, (8.47)

where we regard each particle as being in its own category A, so that the sum over A is

a sum over particles (recall W = αu

). The number density n

can then be calculated

according to equation (5.230), which in spherical symmetry can be taken to be

4π WA

r

. (8.48)

Here we treat the particle as smeared out over a zone size r, which is the radial grid size.

In writing down the ﬁeld equations we want to choose a suitable time coordinate, i.e., a

lapse, that allows us to integrate forward in time without encountering singularities in the

case of black hole formation. Based on our discussion in Section 8.1, where we constructed

the spacetime for a vacuum black hole, we suspect that maximal slicing might provide a

reasonable choice. The maximal slicing condition requires K = 0 = ∂

K (see Chapter

4.2), where we recall K ≡ K

is the trace of the extrinsic curvature. Taking the trace of the

evolution equation for ∂

, i.e., equation (2.137), then leads to a linear elliptic equation

for α,

∂



∂



= α A

)

+ 8πρ + 4π T

(maximal slicing), (8.49)

where T = S − ρ is the trace of T

. Alternatively, we might try polar slicing, for which the

trace of the part of K

transverse to the radial direction is set to zero: K

≡ K

+ K

0. As we have seen in exercise 6.14, and as we will rederive in exercise 8.10, polar slicing