Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

8.3 Fluid stars: collapse 291

function is isotropic and can only depend on the magnitude u ≡ (u

+ u

)

1/2

of the

velocity. In this case we can write d

= (4π u

du)/(1 + u

)

1/2

, which gives ﬁnally

= 4π m



∞

duf

(u)u

(1 + u

)

1/2

. (8.87)

Here the subscript c indicates a value at r = 0and f

(u) ≡ f

(t, r = 0, j = 0, u

= A

u).

Recall from our discussion in Chapter 5.3 that equation (8.84) is solved by applying

Liouville’s theorem in the form of equation (5.231). Speciﬁcally, f at any time t is evaluated

numerically by integrating a trajectory backward in time, from a point (r, u

, j) in phase

space to t = 0, where f is speciﬁed via the initial data. This trajectory is constructed

by integrating ordinary differential equations (8.42) using equation (8.43). The right-hand

sides of these equations involve the values of the ﬁelds and their derivatives, which therefore

must be stored on a radial grid. The time step is chosen according to equation (8.64). A

good check on the method is provided by calculating the total mass-energy of the system

via equation (8.67), which should be conserved in time.

As an example, consider the evolution in maximal slicing of the same truncated, isother-

mal Maxwell–Boltzmann distribution function treated in the previous section by the particle

simulation method.

The point of onset of instability along the equilibrium sequence is

found to be at the same point as before, i.e., the turning point in the binding energy at

= 0.42. The spacetime diagram for the unstable collapse of a collisionless cluster at

= 0.52 is in excellent agreement with the diagram plotted in Figure 8.13. The unique

character of the phase-space method is revealed in Figure 8.20.

Contours of f are plotted on two different slices of ﬁxed j. The phase space coordinates

in the diagram are the freezing variables r

and v

= u

/(Aαu

) measured by a normal

observer. The expectation is that f expressed in these variables should exhibit a steady

conﬁguration at late times when α → 0. This is what is found: once all the matter with a

given j collapses inside the horizon, the distribution function evolves very slowly toward

a ﬁnal static structure.

The phase space method has also been used to demonstrate that it is possible to construct

stable relativistic star clusters with arbitrarily large central redshifts.

Prior to this, it had

generally been believed that all clusters with z

∼

0.5 would be dynamically unstable.

8.3 Fluid stars: collapse

The most important problem to date involving numerical simulations of ﬂuid stars in

spherical symmetry has been the supernova problem. Here the collapse of the degenerate

stellar core of a massive star at the endpoint of stellar evolution is believed to lead to

the formation of a neutron star, accompanied by an explosion of the more massive stellar

envelope. For the most massive stars, core collapse can lead to the formation of a black

Rasio et al. (1989b).

Rasio et al. (1989a).

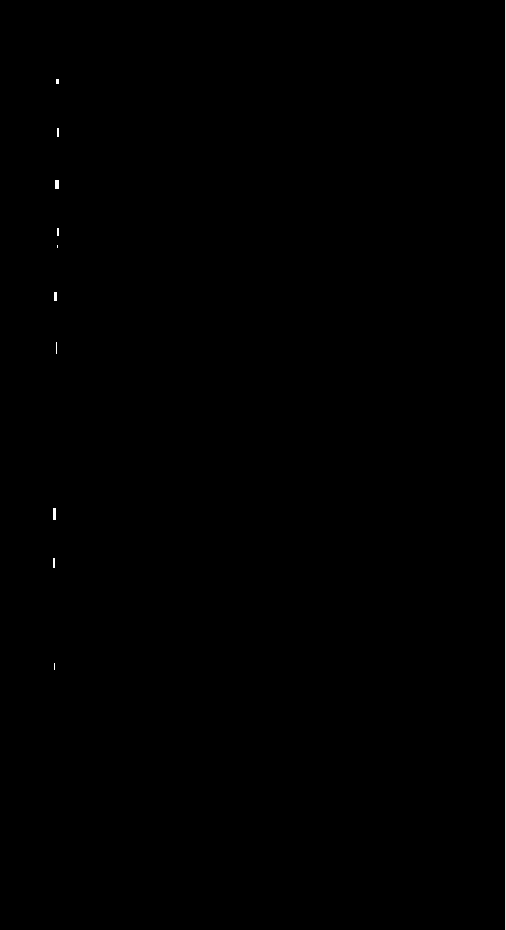
292 Chapter 8 Spherically symmetric spacetimes

1.0

j = 0

j = 0.5

t/M=0

t/M=127

t/M=134

t/M=141

t/M=134

t/M=127

t/M=0

0.5

−0.5

−1.0

1.0

0.5

−0.5

0.5

01 2 Z

/ M

01 2 3

−0.5

−1.0

1.0

Figure 8.20 Time evolution of the distribution function f for the Maxwell–Boltzmann cluster. The areal radius

(in units of M) and the radial velocity v

are used as phase space coordinates. Each plane (r

)isa

2-dimensional slice taken from the 3-dimensional phase space by setting the particle angular momentum j equal

to a constant. The series on the left corresponds to j = 0, while that on the right corresponds to j = 0.5M

representing the angular momentum of a “typical particle” in this cluster (0 ≤ j

∼

for f = 0). Lines of

constant f are shown, equally spaced between 0 and its maximum value on the slice. Note that for j = 0, the

matter never reaches r

= 0. In the ﬁnal plots, the entire mass of the cluster has collapsed inside an event horizon

at r

= 2M.[FromRasio et al. (1989b).]

8.3 Fluid stars: collapse 293

hole instead of a neutron star, with or without an explosion. The demarcation line between

collapse to a neutron star and collapse to a black hole is still uncertain, and all the detailed

microphysical processes (e.g., the “hot” nuclear equation of state; neutrino production

mechanisms and transport, etc.) and all the important macrophysical effects (e.g., general

relativity, rotation, magnetic ﬁelds, convection, etc.) that make up a realistic simulation

are yet to be fully incorporated in a totally rigorous fashion.

One thing is certain: during

stellar core collapse, the gravitational ﬁeld becomes strong and ﬂuid velocities approach

the speed of light, hence a reliable calculation requires a fully relativistic treatment. The

ﬁrst relativistic treatment was the pioneering work of May and White (1966, 1967). Their

work represented an important milestone in computational astrophysics and helped launch

numerical relativity. Their code was based on the formulation of Misner and Sharp (1964)

for spherically symmetric gravitational collapse.

This formulation has the desirable

feature that the equations take the form of Newtonian Lagrangian hydrodynamics plus

relativistic corrections. Hence all the machinery and expertise for handling Lagrangian

hydrodynamics in Newtonian theory could be taken over to the relativistic case. However,

one fundamental problem with the Misner–Sharp formalism and the coordinate system

on which it is based is that collapse to a black hole cannot be followed once the black

hole forms, because the equations become singular. This means that we are unable to

follow the fate of the outer layers of the star when the inner core has formed a black

hole.

Schemes that avoid a singularity during spherical ﬂuid collapse to a black hole have

been constructed by many groups over the years.

The essential feature of these codes

is a different choice of time coordinate from that of Misner and Sharp, which allows

the evolution to be followed to late times, without encountering singularities. Indeed, we

have already shown in Section 8.1 how different time slicings can be chosen to avoid

singularities when evolving a vacuum black hole spacetime, and we then demonstrated in

Section 8.2 that the situation is very similar in the presence of collisionless matter. For

the most part, analogous schemes for ﬂuid matter work on a ﬁxed Eulerian spatial mesh

and adapt the Eulerian equations of relativistic hydrodynamics discussed in Chapter 5.2

to spherical symmetry. In all of these schemes the equations depart much more from

Newtonian hydrodynamics than does the Misner–Sharp formulation. More signiﬁcantly, it

is usually the case that greater computational effort is required in an Eulerian formulation

to attain the accuracy of a Lagrangian formulation. The reason is that the spatial grid in

a Lagrangian scheme follows the ﬂuid elements, so the entire ﬂuid is automatically and

completely covered by the same ﬁxed number of grid points that covered the ﬂuid at the

initial time. Besides the extra effort required to make the hydrodynamics competitive with

For a general discussion and references, see Shapiro and Teukolsky (1983); Arnett (1996); Janka et al. (2007); Burrows

et al. (2007).

The discussion in this section closely follows Baumgarte et al. (1995).

See, e.g., Wilson (1979), Shapiro and Teukolsky (1980); Schinder et al. (1988); Mezzacappa and Matzner (1989)for

early work.

294 Chapter 8 Spherically symmetric spacetimes

a Lagrangian scheme, an Eulerian scheme suffers an additional penalty in treating the

ﬁeld equations. Speciﬁcally, a relativistic Eulerian code typically requires an exterior grid

extending to large distances outside the star in order to impose boundary conditions on

the asymptotically ﬂat gravitational ﬁeld. By contrast, a spherical relativistic Lagrangian

code only needs a grid that covers the matter.

On the other hand, Lagrangian codes are

more difﬁcult to extend to more than one spatial dimension, so they are mainly useful for

spherical systems.

The problem of singularities is irrelevant if collapse always leads to the formation of a

neutron star, in which case the Misner–Sharp formulation is completely adequate. However,

we expect that the collapse of a very massive or supermassive star produces a black hole.

For such cases it is desirable to have a scheme that can handle black hole formation but

with the advantages of the Misner–Sharp formulation. Such a code was developed by

Baumgarte et al. (1995) based on the formulation of Hernandez and Misner (1966), which

uses retarded time as a coordinate instead of the usual Schwarzschild time that appears in

the Misner–Sharp equations. This feature prevents the computational grid following the

ﬂuid from penetrating inside any black hole that may form and encountering a singularity.

In the next section we shall review the widely used Misner–Sharp formulation for spher-

ical hydrodynamics and show how its main deﬁciencies can be easily removed by adopting

the closely related Hernandez–Misner formulation. Both formulations yield Lagrangian

simulation schemes. We postpone a discussion of Eulerian treatments to Chapters 14, 16

and 17, where we describe some important applications of relativistic hydrodynamics in

nonspherical spacetimes.

8.3.1 M isner–Sharp formalism

The Lagrangian equations of relativistic hydrodynamics in spherical symmetry were ﬁrst

derived by Misner and Sharp (1964) and have been used in many numerical calculations,

including those of May and White (1966, 1967).

A straightforward re-derivation of the

equations is contained in Misner et al. (1973)

so we simply summarize the results below.

The line element is written in a diagonal form

=−e

2φ(t, A)

+ e

λ(t,A)

+ R

(t, A)d

, (8.88)

where R is the circumferential radius. In the parlance of 3 + 1, the lapse is e

and the shift

is zero. We can think of each spherical shell of matter as labeled by a parameter A and

Recall that no gravitational waves are generated in spherical symmetry, so there is no need to track their propagation

outside the star.

Exceptions are Lagrangian ﬂuid codes based on the SPH method, which are straightforward to construct for multidi-

mensional spacetimes; see Chapters 5.2, 16 and 17. See also Taub (1978) for shift prescriptions that maintain comoving

(i.e., Lagrangian) coordinates in arbitrary dimensions.

For a robust Eulerian relativistic hydrodynamics scheme speciﬁcally adapted to spherical symmetry, see

Wilson (1979).

See also van Riper (1979).

Misner et al. (1973), exercise 32.7.

8.3 Fluid stars: collapse 295

R(t, A) as the worldline of the shell with label A. The comoving radial coordinate A can

be chosen to be the rest-mass (e.g., baryon number) enclosed within R.

The matter is assumed to be a perfect ﬂuid, for which the stress-energy tensor is given by

equation (5.4) with speciﬁc enthalpy given by equation (5.5). In a comoving (Lagrangian)

coordinate frame, the ﬂuid 4-velocity takes the form

= (e

−φ

, 0, 0, 0). (8.89)

It is useful to deﬁne the quantities

m = 4π



(1 + )R

(∂

R)dA, (8.90)

U = e

−φ

∂

R, (8.91)

 = e

−λ/2

∂

R. (8.92)

Here m can be interpreted as the gravitational mass inside A, U is the coordinate velocity

(rate of change of R along a ﬂuid worldline with respect to the proper time of that ﬂuid

element), and  is simply a more convenient form for the radial metric function.

Note

that since U is only a coordinate velocity, its magnitude may exceed unity.

In terms of these variables the equations of motion and the Einstein ﬁeld equations can

be written as

∂

U =−e



4πR

∂

P +

m + 4π R



, (8.93)

∂

m =−e

4π R

PU, (8.94)

∂

φ =−

∂

P, (8.95)

 = (1 + U

− 2m/R)

1/2

, (8.96)



4π R

∂

. (8.97)

Differentiating equation (8.90) and using equation (8.97) yields

∂

m = (1 + ). (8.98)

Also, equations (8.92) and (8.97) can be combined to give

−λ/2

= 4πρ

. (8.99)

This system of equations still has to be supplemented with the ﬁrst law of thermodynamics

∂

 =−P∂





, (8.100)

Following convention, we use the symbol  in this section to denote the right-hand side of equation (8.92), and γ to

denote the adiabatic index of a perfect gas.

296 Chapter 8 Spherically symmetric spacetimes

as well as an equation of state of the form P = P(ρ

,). For a γ -law EOS we have, as

usual,

P = (γ − 1)ρ

. (8.101)

The appropriate boundary conditions are

R = 0, U = 0,= 1, m = 0 at the origin, A = 0,

P = 0, e

= 1 at the surface, A = A

total

(8.102)

The choice of the boundary condition for φ is somewhat arbitrary; the choice made here

ensures that the coordinate time t agrees with the proper time on the surface of the star.

The above equations deﬁne an initial boundary-value problem for initial data U (R),ρ

(R)

and (R), which have to be chosen such that 1 + U

− 2m/R > 0.

Exercise 8.13 Derive the Newtonian limit of the above equations. Speciﬁcally, take

the limits U  1, 1, P/ρ

 1, and m/R  1toshow

 = 1 = ∂

m. (8.103)

Hence argue that equation (8.103), together with the boundary conditions, implies

that the rest-mass A and the gravitational mass m are the same in the Newtonian

limit. Also argue that equation (8.94) implies that m is now a constant of the motion.

Show that

∂

φ =−

∂

P, (8.104)

from which we conclude that in the Newtonian limit the metric function φ approaches

the Newtonian potential. Argue that φ  1, or e

≈ 1, hence all the evolution

equations can be written independently of φ. Consequently, show that equation (8.91)

becomes

∂

R = U, (8.105)

while equation (8.93) yields the Lagrangian equation of motion for Newtonian

spherical hydrodynamics,

∂

U =−



4π R

∂

P +



, (8.106)

andequation(8.97) becomes

4π R

(∂

. (8.107)

As is apparent from exercise (8.13), an obvious beneﬁt of this coordinate system is that

the relativistic equations are very close to the corresponding Newtonian ones. The meaning

and interpretation of the variables can be carried over directly from the Newtonian theory.

Most important, an existing Newtonian code can easily be upgraded to a fully relativistic

one simply by adding a few terms and equations.

On the other hand, this coordinate system has a severe drawback. If a conﬁguration col-

lapses to a black hole, a coordinate singularity arises which prevents any further evolution.

8.3 Fluid stars: collapse 297

Exercise 8.14 Explore what happens to the lapse function α = e

in comoving

Misner–Sharp coordinates.

(a) Consider ﬁrst the case of dust collapse, where P = 0. Show that α = 1 (geodesic

slicing), and recall the discussion of Chapter 4.1 regarding the ultimate appearance

of coordinate singularities when using this slicing.

(b) Now treat the situation with pressure gradients. Use the Euler equation for the

ﬂuid acceleration a

in the form

=−[∇

P + (u

∇

P)u

] (8.108)

to show that in comoving coordinates

ln α =−

P. (8.109)

Combine equation (8.109) with the second law of thermodynamics for adiabatic

ﬂow to obtain

ln α =−

h, or α ∝

. (8.110)

Comment on the likely consequences of equation (8.110) for calculations of collapse

to black holes.

The singularity problem motivated Hernandez and Misner to introduce a null coordinate

u and transform the above equations to what they called “observer time coordinates”. The

virtue is that these coordinates always stay outside event horizons. Not only are there no

coordinate singularities, but also these coordinates never encounter the physical curvature

singularity at the center of the black hole. We discuss this formalism in the next section.

8.3.2 The Hernandez–Misner equations

Here we summarize the transformations of the equations to observer time coordinates.

The idea is to ﬁnd a coordinate system in which the time coordinate t is replaced by a

null coordinate u, which is constant along outgoing light rays. In addition, u can be scaled

so that it measures the time of an observer at inﬁnity (“observer time coordinates”). For

a conﬁguration that collapses to a black hole, no light ray from inside the event horizon

will, by deﬁnition, ever reach spatial inﬁnity. Therefore no event inside an event horizon

corresponds to ﬁnite “observer time” u; in fact, the event horizon itself is the surface

u →∞.

We introduce the outgoing null coordinate u (outgoing Eddington–Finkelstein coordi-

nate) by

du = e

dt − e

λ/2

dA, (8.111)

Details may be found in Hernandez and Misner (1966)orBaumgarte et al. (1995).

298 Chapter 8 Spherically symmetric spacetimes

whereby the line element (8.88) takes the form

=−e

2ψ

− 2e

λ/2

du dA + R

d

. (8.112)

We note that the lapse function is now given by e

. The equations of the last section can

be transformed to this new coordinate system by transforming the differential operators.

Equation (8.111)gives

−ψ

∂



= e

−φ

∂



, (8.113)

while the chain rule for partial differentiation gives the new spatial derivative in terms of

the old ones according to

−λ/2

∂



= e

−λ/2

∂



+ e

−φ

∂



. (8.114)

The deﬁnition of coordinate velocity U in equation (8.91) becomes

U = e

−ψ

∂

R. (8.115)

Treating the spatial derivative on the right hand side of equation (8.93) with care yields

∂

U =−

1 − v



4πR

∂

P +

m + 4π R



−

1 − v



4πρ

∂

U +

2U



, (8.116)

where v

is the speed of sound given by

= ∂

∗





P ∂



+ ρ

∂





, (8.117)

and where ρ

∗

= ρ

(1 + ) is the total comoving mass-energy density. For a γ -law EOS

the speed of sound can be written

γ − 1

(P + ρ

) = (γ − 1)

h − 1

. (8.118)

Exercise 8.15 Derive equation (8.118) for the sound speed from equation (8.117).

The remaining Einstein equations (8.94), (8.92), and (8.97) now become

∂

m =−e

4π R

PU (8.119)

 = (1 + U

− 2m/R)

1/2

(8.120)

 + U

4π R

∂

. (8.121)

See Appendix B of Baumgarte et al. (1995).

8.3 Fluid stars: collapse 299

An integration factor e

was inserted in equation (8.111)tomakedu a perfect differential.

This requirement yields a differential equation to replace equation (8.95):

∂

ψ =



∂

U +

4πρ



 R

. (8.122)

Using equation (8.114) to replace the spatial derivative in equation (8.98), as well as

equation (8.94), yields

∂

m = (1 + ) −

. (8.123)

Once again, the equations have to be supplemented by the ﬁrst law of thermodynamics for

adiabatic ﬂow,

∂

 =−P∂





, (8.124)

together with an EOS, P = P(ρ

,).

The boundary conditions are mostly the same as in the Misner–Sharp scheme described

in the last section:

R = 0, U = 0,= 1, m = 0 at the origin, A = 0,

P = 0, e

=  + U at the surface, A = A

total

(8.125)

Exercise 8.16 Show that the boundary condition for ψ matches the interior u

to the exterior, where observer time coordinates reduce to outgoing Eddington–

Finkelstein coordinates. Begin by noting that for an observer comoving with the

ﬂuid at the surface of the conﬁguration,

=−e

2φ

=−dt

. (8.126)

Next, express the exterior spacetime at the surface in Schwarzschild coordinates,

=−(1 −2M/R)dt

+ (1 −2M/R)

−1

+ R

d

, (8.127)

to ﬁnd dt

/dt, then express du in terms of the same coordinates,

du = dt

− (1 −2M/R)

−1

dR, (8.128)

to ﬁnd du/dt. Combine with equation (8.111) to get the desired result.

Note that the boundary condition for ψ implies that u measures the proper time of a

stationary observer at inﬁnity (cf. equations 8.127 and 8.128).

The Newtonian limit of the above equations results in the same equations found in the

Newtonian limit of the Misner–Sharp equations and derived in exercise (8.13). The result

is not surprising, since the Newtonian limit corresponds to setting c =∞, in which case

the light cones along which u = constant open up and coincide with t = constant surfaces.

In the Newtonian limit, ψ disappears from the equations, as did φ in the previous case.

300 Chapter 8 Spherically symmetric spacetimes

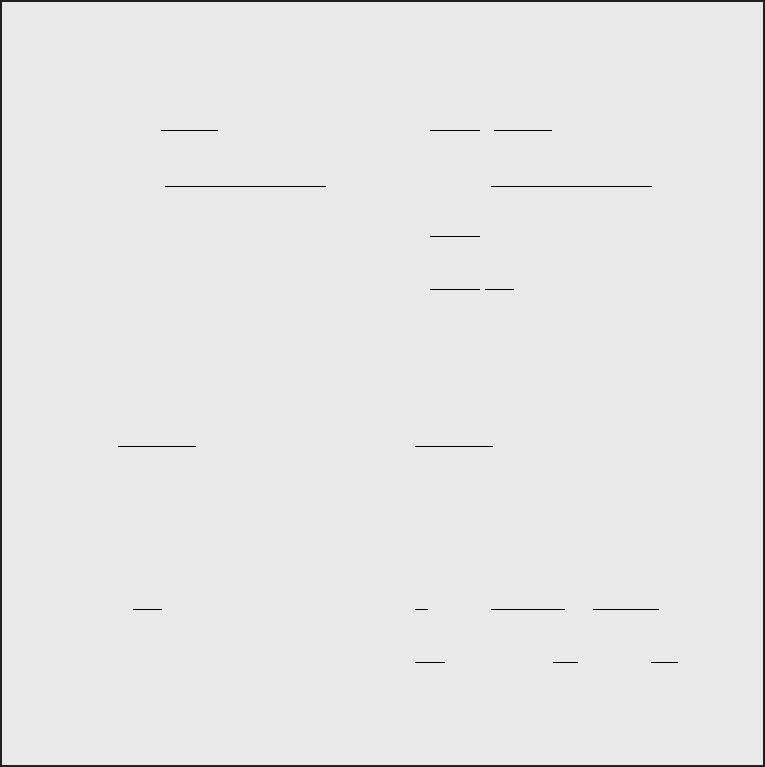
Box 8.1 The Misner–Sharp and Hernandez–Misner equations

For an easy comparison we list the equations of Misner and Sharp (1964) in the left column and

those of Hernandez and Misner (1966) in the right column:

∂

U =−e



4πR

∂

(P + P

vis

) ∂

U =−

1 − v



4πR

∂

(P + P

vis

)

m + 4π R

(P + P

vis

)



m + 4π R

(P + P

vis

)



−

1 − v



4πρ

∂

U + 2U /R



1 − v



∂

vis

∂

R = e

U ∂

R = e

∂

m =−e

4π R

(P + P

vis

)U ∂

m =−e

4π R

(P + P

vis

 = (1 +U

− 2m/R)

1/2

 = (1 +U

− 2m/R)

1/2



4π R

∂

 + U

4π R

∂

 =−(P + P

vis

)∂

(1/ρ

) ∂

 =−(P + P

vis

)∂

(1/ρ

)

h = 1 + + (P + P

vis

)/ρ

h = 1 + + (P + P

vis

)/ρ

∂

m = (1 + )∂

m = (1 + ) − (P + P

vis

)U/ρ

∂

φ =−

∂

(P + P

vis

) ∂

ψ =



∂

U +

4πρ



P + P

vis

 R



(P + P

vis

)

∂ P

∂



+ ρ

∂ P

∂ρ







We list the equations in the order in which they are typically evaluated in a numerical scheme. For

completeness we explicitly include an artiﬁcial viscosity term P

vis

(see equation 5.24).

A summary of the two sets of equations appears in Box 8.1. All relevant equations are

listed next to each other and in the order in which they should be evaluated in a numerical

scheme.

We remark that the u = constant surfaces are not characteristics of the Hernandez–

Misner equations. This is because there is no gravitational radiation in spherical symmetry.

Therefore we are still dealing with a Cauchy problem for the ﬂuid evolution, rather than

a characteristic initial value problem, and both the Misner–Sharp and Hernandez–Misner

equations can be treated in the same way.

For a ﬁnite difference version of the Misner–Sharp equations, see van Riper (1979) and for the Hernandez–Misner

equations, see Baumgarte et al. (1995).