Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

8.2 Collisionless clusters: stability and collapse 271

avoids regions of spacetime containing trapped surfaces in spherical symmetry, suggesting

that it might have better singularity avoidance than maximal slicing when a black hole

forms. The lapse equation for polar slicing is a simple quadrature,

α =



1 −



max





exp





max

r(∂

A/A)

+ 8πrS

1 +r∂

A/A



(polar slicing), (8.50)

where r

max

is an arbitrary radius in the vacuum exterior (see exercise 8.8). Both maximal

and polar slicings have been used in simulations of collisionless clusters.

It is convenient to use the quantity K

to express equations that are valid in both maximal

and polar gauges:



0 (polar slicing),

−K

(maximal slicing).

(8.51)

Then the evolution equation (2.134) for the metric coefﬁcient A is

∂

A = β



∂

A +



−

α AK

. (8.52)

The Hamiltonian constraint (2.132) becomes a nonlinear elliptic equation for A,

∂



∂

1/2



=−

5/2



8πρ +



. (8.53)

We used up our spatial coordinate freedom by choosing the 3-metric to be isotropic.

This choice automatically leads to a condition on the shift, β. This shift condition may be

derived by using the deﬁnition of K

, equation (2.134), to evaluate α(K

− K

θθ

), which

yields

∂





− K

), (8.54)

β =−r



∞

α(K

−

)

(8.55)

(cf. exercise 4.12).

Exercise 8.6 In spherical symmetry, a “ﬁrst-order form” of the minimal distortion

gauge (cf. equation 4.70) may be written

(Lβ)

= 2α(K

−

K γ

), (8.56)

where the vector gradient (Lβ

) of the vector β

is deﬁned in equation (4.67).

Show that equation (8.54) is consistent with condition (8.56).

For spherical systems, the ﬁrst-order form of the minimum distortion condition is sufﬁcient, since there are no radiative

modes and only longitudinal shear is present. See equations (4.71)or(4.74) for the second-order form of the minimal

distortion condition.

272 Chapter 8 Spherically symmetric spacetimes

The momentum constraint (2.133) determines the radial component of the extrinsic

curvature:

− D

K = 8π S

, (8.57)

which yields













8π/(A

)





dr (maximal slicing),

4πrS

/(1 +r∂

A/A) (polar slicing).

(8.58)

The relevant ﬁeld equations have now all been assembled. We point out again that in

spherical symmetry, which contains no dynamical degrees of freedom, it is not necessary

to solve an evolution equation either for the one nontrivial 3-metric coefﬁcient A or

the one independent extrinsic curvature variable K

. These quantities on any time slice

are determined entirely by the Hamiltonian and momentum constraint equations. Hence,

we may solve the Hamiltonian constraint equation (8.53)forA in lieu of the evolution

equation (8.52), and similarly for K

. The resulting approach constitutes a completely

constrained evolution scheme.

Exercise 8.7 Derive ﬁeld equations (8.52)–(8.58). To do so you will ﬁrst need to

use the isotropic metric (8.41) to calculate the following quantities:

(a) 

for all i, j, k,

Hint: Use equation (3.7) with ¯γ

= (1, r

, r

sin

θ) to obtain



= ∂

A/A,

θθ

=−(r +r

∂

A/A),



rθ

= 

rφ

= 1/r + ∂

A/A,

φφ

=−sinθ cosθ,



φφ

=−r sin

θ −r

sin

θ∂

A/A,



θφ

= cotθ.

(b) R

Hint: Use equation (3.10)toﬁnd

=−2A

−3

[∂

∂

A +

∂

A −

(∂

=−A

−3

[∂

∂

A +

∂

A] = R

(d) K

Hint: Use equation (2.135)toshow

=−[∂

− 2∂

+ 2β

∂

A/A]/(2α),

θθ

=−[∂

− 2β

(1/r + ∂

A/A)]r

/(2α)

= K

φφ

sin

−2

θ,

where β

= A

β.

(e) K = K

8.2 Collisionless clusters: stability and collapse 273

Exercise 8.8 (a) Derive the maximal slicing condition (8.49).

(b) Derive the polar slicing condition (8.50).

Hint: Deﬁne d/dt ≡ ∂

− β

∂

. Then show that

=−∂

+ ∂

− D

α + α[R

+ KK

+ 4π T δ

− 8π S

(8.59)

Set K

= K

+ K

, use equation (8.59), and demand that K

= 0 = dK

/dt.

To solve the ﬁeld equations uniquely we need boundary conditions. Outer boundary

conditions are obtained by matching the metric to the isotropic form of the static Schwarz-

schild metric as r →∞. In fact, it is easy to show that in polar slicing, the metric takes

the isotropic Schwarzschild form everywhere in the vacuum exterior. Set the right hand

side of equation (8.53) equal to zero and integrate. Requiring that A tend asymptotically

to the isotropic value at large r yields

A =



1 +



(polar slicing, exterior) (8.60)

for all r outside the matter. Substituting this result into equation (8.50), with S

= 0,

gives

α =

1 − M/(2r)

1 + M/(2r)

(polar slicing, exterior), (8.61)

which is the familiar isotropic lapse function. Equation (8.58)showsthatK

= 0every-

where outside the matter, and hence by equation (8.55), β = 0 as well. Thus in polar slicing

one need only integrate Einstein’s equations inside the matter and match to the standard

Schwarzschild metric in isotropic coordinates at the matter surface. By contrast, in maxi-

mal slicing, the nonzero β and K

require the metric to be integrated to reasonably large

values of r  M in the vacuum exterior in order to match to the standard Schwarzschild

line element. For maximal slicing at large r matching yields A → 1 + const/r to leading

order in 1/r , and similarly for α. This behavior can be imposed by setting a Robin boundary

condition at the outermost grid point, ∂

[r(A − 1)] = 0, and likewise for α. Equation (8.58)

gives K

∼ r

−3

as r →∞, so that the asymptotic solution to equation (8.55)is

β =

(

1 +

O(1/r)

)

(maximal slicing, large r ). (8.62)

The boundary conditions for the ﬁeld variables at the center of the cluster are chosen to

enforce regularity, which is appropriate for a matter proﬁle that is smooth near the origin

and exhibits no spikes (e.g ∂

ρ = 0 = S

,etc.):

0 = ∂

α = ∂

A = β = K

(r → 0). (8.63)

Solving the Hamiltonian equation (8.53) numerically for A

1/2

by ﬁnite-differencing in

r to replace the second-order differential operator requires linearization of the right-hand

274 Chapter 8 Spherically symmetric spacetimes

side. The resulting set of coupled, linear equations, differenced to second order in the

grid spacing r, typically takes on a tridiagonal form, for which simple recipes exist for

inverting the matrix. Linearization requires iteration of the solution until convergence.

Using the evolution equation for A to provide a good initial guess on the new time slice,

given its value on the previous slice, usually accelerates the convergence. The maximal

slicing condition (8.49) yields a similar tridiagonal set of equations, but this equation is

linear in α, so no iteration following inversion is necessary. The other ﬁeld equations may

be solved either algebraically or by simple one-dimensional, numerical quadrature.

Since there are no ﬁeld evolution equations to solve in a completely constrained code,

and only ODEs for the matter, the time step t between computational time slices is not

subject to a hyperbolic Courant condition (e.g., the light-travel time across a radial grid

spacing; see Chapter 6.2.3). Rather, it is determined by the time scale for the matter source

terms to change, i.e., the dynamical time scale of the system. A reasonable time-step

criterion that has worked in practice is

t ≈ min





3π

32ρ



1/2



, (8.64)

where q

∼

0.1 is a constant. Here the quantity in parantheses is the free-fall collapse time

for a homogeneous dust ball at the local density ρ. The insertion of α in the denominator

accounts for the slowing down of proper time with respect to coordinate time as the lapse

function falls to zero. Equation (8.64) still guarantees that the matter source terms change

only a small amount between time steps, because they change only when proper time as

measured by a normal observer (dτ = αdt) increases by a signiﬁcant fraction of the local

free-fall time.

Diagnostics

As in any simulation, one can identify a number of nontrivial diagnostics that provide a

check on the accuracy of the numerical simulation. For example, the total mass-energy of

the conﬁguration M = M

ADM

, which can be computed as in equation (3.145)or(3.147),

must remain constant in time. In fact, in a spherical spacetime, one can use the con-

servation of mass-energy to prove additional constraints on the metric, as suggested by

exercise (8.9).

Exercise 8.9 Everywhere in the vacuum exterior of a spherical spacetime, M may

be expressed invariantly as

M =



16π



1/2



1 −

∇

A∇

16πA



, (8.65)

See Chapter 6.2.2.

8.2 Collisionless clusters: stability and collapse 275

where A is the proper area of a 2-sphere of radius r.

Evaluate equation (8.65)to

show that in the coordinates adopted in this section we have

A = 4π A

(8.66)

and

M =

1 +

(Ar K

)

−



1 +

∂



. (8.67)

The expression appearing on the right-hand side of equation (8.67) must therefore be

constant in space and time throughout the vacuum exterior and must equal the initial

mass-energy of the conﬁguration. This provides a useful self-consistency check on the

integrations. In the case of polar slicing, where A is given by equation (8.60), the identity

is satisﬁed trivially. The check in this case thus reduces to seeing whether the expression

for M formed from the gradient of A is continuous at the matter surface.

A further check is available for stable, equilibrium clusters. Since the metric is static in

such a case, each particle has a conserved energy, E =−p

. It is thus useful to check for

the conservation of the total particle “energy”,

−E

≡



. (8.68)

In cases where the cluster collapses to a black hole, it is useful to follow the growth

of the black hole event horizon. This can be done easily in spherical symmetry simply

by calculating the trajectories of outgoing radial null rays emitted from various spacetime

points. The geodesic equation for the jth ray is

α(t, r

)

A(t, r

)

− β(t, r

). (8.69)

The location of the event horizon is then found by ﬁnding pairs of null rays emitted from

the same radius at slightly different times, one of which escapes to inﬁnity and one of

which is pulled back into the hole.

Inside the black hole there can be trapped surfaces, i.e., regions where the cross-sectional

area of an outgoing bundle of null rays immediately converges.

In spherical symmetry

this condition can be expressed simply by the equation

≤ 0, (8.70)

where d/dt is the total derivative along the null ray and

A is given by equation (8.66)for

a radially propagating bundle of null rays spanning a 2-sphere. Using equations (8.52)and

See Lightman et al. (1975), problem 16.10.

See Chapter 7.2.

Recall Chapter 7.3.

276 Chapter 8 Spherically symmetric spacetimes

(8.69), we ﬁnd that condition (8.70) becomes

1 +r(∂

A)/ A − Ar K

/2 ≤ 0. (8.71)

Recall that the apparent horizon is the outer boundary of the region of trapped surfaces

and occurs where equality holds in equations (8.70) and (8.71). In polar slicing, where

= 0, trapped surfaces do not form, as shown in exercise 8.10.

Exercise 8.10 Show that the existence of trapped surfaces in polar slicing would

be equivalent to the condition

≤ 0, (8.72)

where r

= Ar is the Schwarzschild areal radial coordinate. Thus argue that in a

nonpathological spacetime where r

is a monotonic increasing function of r,no

trapped surfaces are encountered.

For collapse to a black hole, trapped surfaces are generally found in maximal slicing, but

the polar slices avoid these regions. Thus polar slicing has a somewhat stronger “singularity

avoidance” property than maximal slicing.

α-Freezing

Integrating the above system of equations yields very accurate numerical spacetimes for

the most part, as we shall illustrate below. However, some simulations of collapsing clusters

become inaccurate before the exterior spacetime surrounding the growing, central black

hole reaches a ﬁnal stationary state. This problem can be particularly severe for clusters with

appreciable central mass concentration – so-called “extreme core-halo conﬁgurations”.

Such clusters are characterized by enormous dynamic range, with orbital timescales in

the central core much shorter than those in the outer halo. A “seed” black hole forms at

the center well before the bulk of the matter in the outer regions has had time to evolve

signiﬁcantly. Determining what fraction of the total cluster mass ultimately forms a black

hole and what fraction remains outside in orbit about the hole can prove challenging in such

cases. Yet the outcome may shed light on plausible mechanisms for forming supermassive

massive black holes in the cores of collisionless clusters arising in nature, like dense star

clusters or dark matter halos.

The traditional way of attacking this issue is to ﬁnd coordinate conditions (i.e., lapse

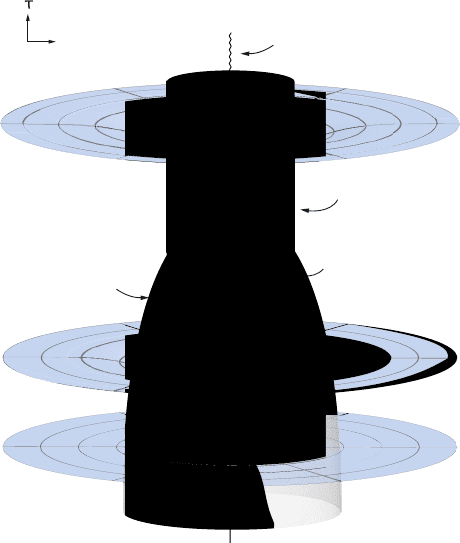
and shift functions) that make the problem trackable. Figure 8.8 illustrates the main effect

responsible for the inability of the choices discussed in this section to track the late-time

evolution of extreme core-halo conﬁgurations. Isotropic coordinates, while preventing

“spikes” from forming in the radial metric component near horizons, lead to consider-

able grid stretching all along the black hole throat. Grid stretching arises because the

See also exercise 7.13, where the result is derived by a more formal route.

8.2 Collisionless clusters: stability and collapse 277

singularity

=2M

matter

surface

event horizon

Figure 8.8 Schematic spacetime diagram of the collapse of a collisionless cluster to a black hole. The vertical

axis measures proper time τ measured by a normal observer and the horizontal axis measures areal

(Schwarzschild) radius r

. A singularity forms at the center in a ﬁnite proper time. The time slicing chosen here

avoids the singularity by “slowing down” the advance of proper time near the center, hence the warping there of

the spatial hypersurfaces with increasing coordinate time t . Spherical polar coordinate lines appearing on each

slice mark the spatial grid, with the radial grid based on an isotropic coordinate r. When the spatial metric on the

time slice t has the “radial” form A

d

, a spike develops in A

near the event horizon, as in the usual

static Schwarzschild geometry. When the isotropic metric A

+ A

d

is used, no spike appears. However,

considerable radial grid must be expended along the throat near the horizon to determine the metric accurately

(“grid stretching”). [After Shapiro and Teukolsky (1986).]

isotropic radial coordinate r must span many decades along the black hole throat. The

metric ﬁeld also varies rapidly on the throat. Consequently, it is necessary to cover the

throat with an increasing number of grid points to determined the metric accurately in

a numerical calculation. But given ﬁnite computational resources, there are only a ﬁnite

number of radial grid points available to cover the throat. The result is that the growing

numerical inaccuracies attributed to grid stretching ultimately force the integrations to

terminate.

In addition, maximal time slicing, although successful in holding back the advance of

proper time at the center and thus postponing the appearance of singularities, causes the

lapse function α to decay and the spatial conformal factor A to increase exponentially

278 Chapter 8 Spherically symmetric spacetimes

at late times near the center. This can eventually cause underﬂows and overﬂows in the

computed metric components whenever a black hole forms, forcing the integrations to

terminate before the exterior spacetime reaches a ﬁnal stationary state.

Several techniques have been developed that allow us to evolve black holes for very

long times, without the occurence of the above problems. One such technique is black

hole excision;

another is the “moving-puncture” approach.

However, in the case of

collisionless particles undergoing spherical collapse to a black hole, there is a very simple

and elegant choice of coordinates and matter variables that provide accurate solutions for

arbitrary late times. The idea behind this choice is easily understood. At late times during

the collapse the lapse goes to zero exponentially with t near the cluster center (the “collapse

of the lapse”; see Chapter 4.2). Hence the proper time interval dτ = αdt measured by a

normal observer near the cluster center goes to zero for a ﬁnite interval of coordinate time

dt. Thus we expect that any physical quantity measured by such an observer will freeze,

i.e., become constant with t, at late times, because there is no advance of proper time in

that observer’s reference frame.

As an example, consider the radial component of the velocity of a particle, v

, where the

caret denotes an orthonormal component measured by the normal observer n

.Wehave

= u

=−u

(

, (8.73)

where e

(

= n

is the orthonormal time basis vector and e

(

= e

/A is the orthonormal

radial basis vector. Evaluating equation (8.73) yields

= (u

/A)/αu

(8.74)

and similarly

= (u

/Ar )/αu

. (8.75)

Substituting equations (8.74) and (8.75)into(8.43)gives

αu



1 − (v

)

− (v

)



−1/2

. (8.76)

Since v

and v

must freeze at late times, so must αu

, and since u

is a constant of

the motion, we learn from equations (8.74) and (8.75) that the areal radius of a particle

= Ar and the ratio u

/A also freeze.

In this fashion it is straightforward to determine which quantities freeze and which do

not as α → 0. We ﬁnd that, as functions of r

, the source functions ρ and S freeze, while S

and S

do not. The quantities β, A and r (the isotropic radius of a particle) do not freeze.

Equation (8.42) thus shows that even when α → 0, the shift continues to drive changes in

r. The result is grid stretching.

See Chapters 13.1.2 and 14.2.3 ff.

See Chapter 13.1.3.

8.2 Collisionless clusters: stability and collapse 279

To overcome grid stretching one needs to take advantage of α-freezing and recast the

equations in terms of the freezing variables. In either polar or maximal time slicing, the

equations of motion of a particle become

=−

αr

+ α

/A)

αu



1 −

∂



−1

, (8.77)

d(u

/A)



−(αu

)∂

α + α

(αu

)





1 −

∂



−1

+ αK

/A). (8.78)

Since every term on the right-hand sides of the above equations contains an explicit factor

of α or ∂

α, we see that

→ 0,

d(u

/A)

→ 0asα → 0. (8.79)

This provides a formal proof of the freezing of the particle motion at late times near the

center of a collapsing conﬁguration in either maximal or polar slicing.

In the next section

we will present results of simulations, some of which utilize freezing variables.

Numerical calculations

As a test of the overall mean-ﬁeld, particle simulation scheme, consider the results obtained

for Oppenheimer–Snyder collapse, i.e., the collapse from rest of a spherical, homogeneous

dust ball to a Schwarzschild black hole, as discussed in Chapter 1.3. The interior is given

by the familiar Friedmann solution for a closed universe, which is known in closed analytic

form in Gaussian normal (geodesic) time and comoving spatial coordinates. The interior

must be matched smoothly onto the vacuum exterior, which is just the static, vacuum

Schwarzschild metric. For comparison with a numerical simulation, it is necessary to

express the solution in the same coordinate system used in the simulation. The transfor-

mation of the Oppenheimer–Snyder solution to both maximal and polar time slicing and

isotropic spatial coordinates has been carried out

in order to compare numerical with

analytic solutions in these gauges.

In Figure 8.9 the lapse proﬁle is plotted on selected maximal time slices during the

collapse from an initial areal radius R/M = 10. The agreement between the analytic

and numerical solutions is good, even after the black hole forms at t/M ≈ 40. Freezing-

variables were not required for this example. A spacetime diagram is plotted in Figure 8.10,

showing that numerical code tracks the matter worldlines fairly reliably. It is also reassuring

that the event horizon appears ﬁrst at the origin and grows monotonically outwards,

remaining stationary at r

/M = 2 once the last particle crosses inside. Not surprisingly,

the stellar surface approaches a limit surface at r

/M = 3/2; this is the same limit surface

For the detailed form of the ﬁeld equations using freezing variables, see Shapiro and Teukolsky (1986).

Petrich et al. (1985, 1986).

280 Chapter 8 Spherically symmetric spacetimes

Figure 8.9 The lapse α as a function of areal radius r

on selected maximal time slices for Oppenheimer–Snyder

collapse from R = 10M . The solid lines are the results of exact integrations. The dots are the results obtained

with the numerical code. [From Shapiro and Teukolsky (1985b).]

that we found when we evolved a vacuum Schwarzschild spacetime in maximal time slicing

in Section 8.1. Maximal slicing is successful in holding back the collapse and preventing

the formation of central singularity, but not before the matter collapses deep inside the

event horizon. By contrast, in polar slicing, the matter surface asymptotes to r

/M = 2

and no trapped surface forms, as depicted in Figure 8.11.

A more interesting case is the evolution of a collisionless ensemble of identical particles

initially in equilibrium and described by a truncated, isothermal Maxwell–Boltzmann

distribution function,

f (E) =



K exp(−E/T ), E ≤ E

max

0, E > E

max

(8.80)

Here K is a normalization constant, T is a constant “temperature”, E =−p

is the

energy of a particle, and E

max

is the maximum allowed energy, corresponding to a particle

momentarily at rest at the surface of the conﬁguration, r

= R. The energy cutoff guarantees

that all particles are restricted to a ﬁnite region of space.