Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

8.2 Collisionless clusters: stability and collapse 281

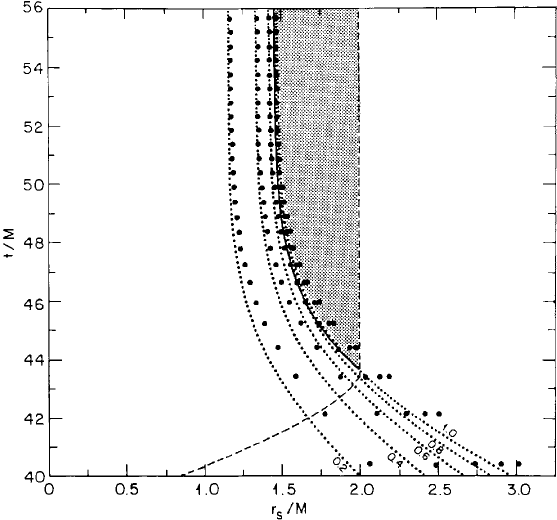
Figure 8.10 Spacetime diagram at late times for Oppenheimer–Snyder collapse in maximal slicing

from R = 10M. The dotted lines are worldlines of Lagrangian matter elements from exact integrations.

Each worldline is labeled by the ﬁxed interior rest-mass fraction. The dots are points for the corresponding

elements obtained with the numerical code. The dashed line is the event horizon. The shaded area is the

region of trapped surfaces. Its outer boundary, the apparent horizon, coincides with the event horizon. Its inner

boundary is just inside the surface of the matter. [From Shapiro and Teukolsky (1985b).]

Relativistic star clusters in equilibrium with truncated Maxwell–Boltzmann distributions

have been studied extensively in the literature.

Prior to the development of numerical

relativity such studies were restricted to the construction of static equilibria and depended

on linear perturbation theory employing trial functions to analyze stability. The precise

point of onset of dynamical instability along parametrized sequences of equilibria could

not be determined by this approach. However, by using these models as initial data in

a relativistic mean-ﬁeld, particle simulation scheme, the point of onset of dynamical

instability can be rigorously identiﬁed and, more signiﬁcantly, the full nonlinear evolution

of unstable systems can be tracked and their ﬁnal fate ascertained.

As an example, consider the evolution of a Maxwell–Boltzmann cluster with areal

radius R/M = 9.2 and central gravitational redshift z

= 0.52 along a one-parameter

equilibrium sequence deﬁned by E

max

= m − T /2, where m is the mass of each particle,

assumed identical. This cluster is only moderately centrally condensed, with the ratio of

See, e.g., Zel’dovich and Podurets (1965); Ipser (1969b); Misner et al. (1973); Katz et al. (1975) for models.

282 Chapter 8 Spherically symmetric spacetimes

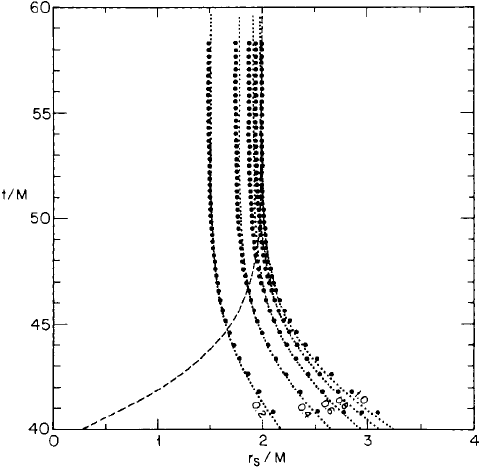
Figure 8.11 Spacetime diagram at late times for Oppenheimer–Snyder collapse in polar slicing from R = 10M.

The labelling is the same as in Figure 8.10. No trapped surface forms in this slicing. [From Shapiro and

Teukolsky (1986).]

mean-to-central mass-energy density given by ρ/ρ

= 0.072. It lies just beyond the point

of onset of instability, which is near z

= 0.42, as determined by numerical simulations.

The collapse of this cluster has been followed using both maximal and polar time slicing

and isotropic radial coordinates.

Snapshots of the conﬁguration are shown at selected

maximal times during the collapse in Figure 8.12.

By solving equation (8.69) and identifying pairs of outgoing null rays emitted at neigh-

boring points in spacetime, one of which escapes to inﬁnity and the other of which is pulled

back by the black hole, the location of the black hole event horizon was determined. By

solving equation (8.71) in maximal slicing, the region of trapped surfaces and the apparent

horizon were identiﬁed. All the matter collapses inside the black hole and the surface

approaches a limit surface at r

/M = 1.5 in this time slicing, As expected, both horizons

merge and remain locked at r

/M = 2 once the last particle is captured. In polar slicing

the collapsing surface asymptotes to radius r

/M = 2 at late times and no trapped surface

forms. A spacetime diagram showing the late-time behavior is shown in Figure 8.13 for

maximal slicing and in Figure 8.14 for polar slicing. Once again, freezing variables were

not required for this integration.

A more computationally challenging example is provided by the collapse of an unstable

equilibrium cluster with an extreme core-halo proﬁle. Consider a relativistic, collisionless,

Shapiro and Teukolsky (1985a, 1986).

8.2 Collisionless clusters: stability and collapse 283

Figure 8.12 The collapse of a marginally unstable gas of collisionless particles of arbitrary mass M which at

t = 0 obeys a truncated, isothermal Maxwell–Boltzmann distribution function with an areal radius R/M = 9.

Spherical ﬂashes of light are used to probe the spacetime geometry; at late times the light rays are trapped by the

gravitational ﬁeld. Their trajectories help locate the black hole event horizon, which in this example eventually

reaches r

/M = 2 and encompasses all the matter. [From Shapiro and Teukolsky (1988).]

spherical polytrope of index n = 4 with a central redshift z

= 0.50. The phase space

distribution function for such a conﬁguration has the form

f (E) =



K (E/E

max

)

−5

[1 − (E/E

max

)

]

5/2

, E ≤ E

max

0, E > E

max

(8.81)

where the variables have the same deﬁnitions as in equation (8.80). In this case, the

relativistic core contains only 0.5% of the total rest-mass. The remainder of the mass

Fackerell (1970).

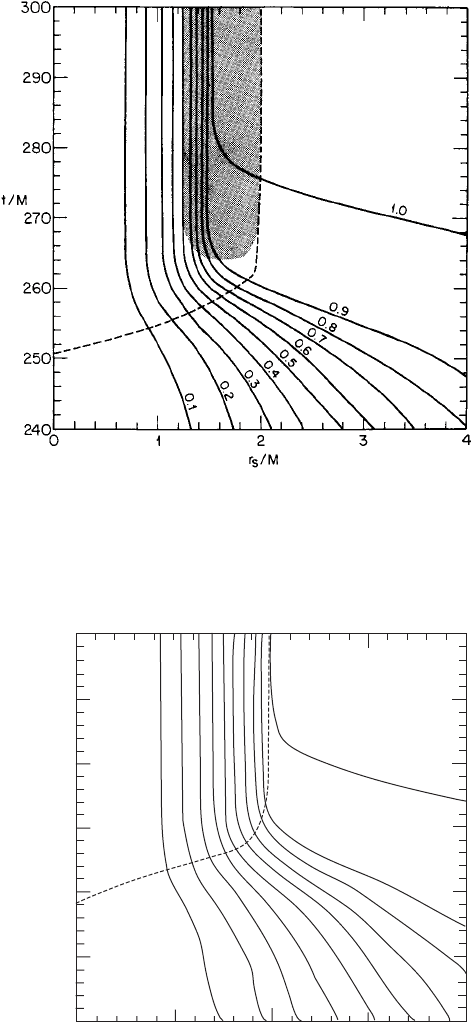
Figure 8.13 Spacetime diagram in maximal slicing for the Maxwell–Boltzmann cluster depicted in Figure 8.12.

The solid lines are worldlines of ﬁctitious Lagrangian matter tracers labeled by the ﬁxed interior rest-mass

fraction. The dashed line is the event horizon. The shaded area is the region of trapped surfaces. The event and

apparent horizons are both numerically asymptote to r

= 2M to high accuracy. [From Shapiro and Teukolsky

(1986).]

300

290

280

270

t / M

260

250

240

012

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

Figure 8.14 Spacetime diagram in polar slicing for the Maxwell–Boltzmann cluster depicted in Figures 8.12

and 8.13. Labeling is the same as in Figure 8.13. No trapped surface forms in polar slicing. The event horizon

and matter surface are both numerically asymptote to r

= 2M to high accuracy. [From Shapiro and Teukolsky

(1986).]

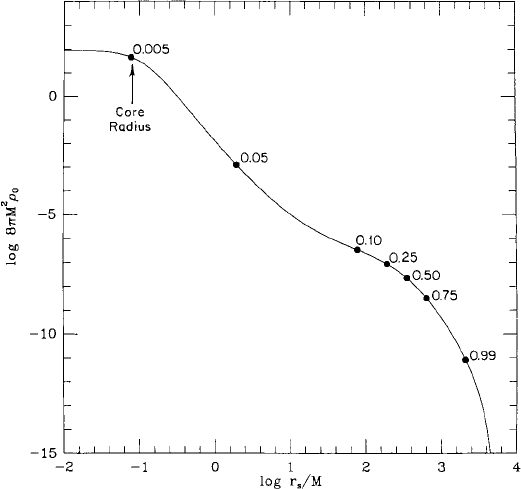
8.2 Collisionless clusters: stability and collapse 285

Figure 8.15 Initial rest-mass density proﬁle ρ

for the relativistic polytrope with n = 4, = 5/4, and

central redshift z

= 0.50. Dots are located at points at which the interior rest-mass fraction has the values

shown. This extreme core-halo conﬁguration has a highly relativistic core and an extensive Newtonian halo. A

the end of the simulation, the black hole which forms at the center contains a fraction 0.05 of the total rest-mass,

approximately 10 times the initial core mass. [From Shapiro and Teukolsky (1986).]

resides in a nearly Newtonian halo extending out to R/M ≈ 5000. The ratio of the mean-

to-central density in the cluster is tiny: ρ/ρ

= 4.0 × 10

−13

; see Figure 8.15.

The cluster is dynamically unstable. During its collapse, approximately 5% of the cluster

mass, considerably more mass than the core, forms a central black hole. By the end of

collapse, the cluster settles into a new equilibrium state consisting of a massive Newtonian

halo of particles in orbit about a central black hole. Such a centrally condensed system

could provide a plausible model of a galaxy containing a supermassive black hole.

The

catastrophic collapse of an unstable, collisionless gas like the one evolved here might even

provide a viable formation mechanism for such a supermassive black hole.

Supermassive

black holes are believed to be the engines that power quasars and active galactic nuclei and

their formation and growth remains one of the major puzzles of cosmological structure

formation.

Most galaxies containing a bulge, including the Milky Way, are observed to contain a central supermassive black hole;

see, e.g., Ho (2004) for reviews and references.

Zel’dovich and Podurets (1965); Rees (1984); Shapiro and Teukolsky (1985c); Balberg and Shapiro (2002).

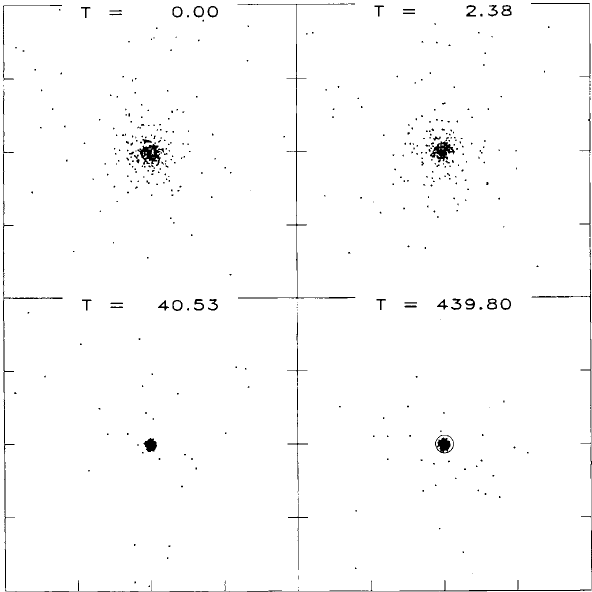
286 Chapter 8 Spherically symmetric spacetimes

Figure 8.16 Snapshots of the central regions r

/M ≤ 2 during the collapse of the extreme core-halo

conﬁguration shown in Figure 8.15. The markers on frames are placed at intervals of r

= 1M.Thetimesare

labeled by T ≡ t/M. The circle in the last frame shows the event horizon at r

/M = 0.1. The collapse of the

innermost regions to a black hole is evident. By t/M ≈ 40, the cluster reaches a quasistationary state consisting

of central black hole surrounded by a massive halo of orbiting particles. [From Shapiro and Teukolsky (1986).]

Freezing-variables, designed to handle conﬁgurations with large dynamic range, are

required to follow the evolution of this cluster reliably.

Maximal slicing is not adequate

to hold back the collapse, as the value of the central radial metric coefﬁcient increases

above A

≈ 10

and the central lapse falls below α

≈ 10

−70

, leading to inaccuracies due

to excessive grid stretching. Polar slicing with freezing variables proves necessary, in part

because A

grows much more slowly in this gauge.

Highlights of the collapse are summarized in Figures 8.16–8.18. Snapshots of the

imploding central parts of the cluster inside r

/M = 2 are shown at selected times in

Figure 8.16. There is little evolution in the outer Newtonian halo where most of the mass

resides. However, the growing black hole is effective in “sweeping clean” the innermost

Shapiro and Teukolsky (1986).

8.2 Collisionless clusters: stability and collapse 287

Figure 8.17 Spacetime diagram in polar slicing for the relativistic polytrope shown in Figure 8.16. Labeling is

thesameasinFigure8.13. The event horizon asymptotes to r

/M = 0.1, at which point it encompasses 5% of

the total cluster rest-mass. [From Shapiro and Teukolsky (1986).]

region in and around the core. The cluster settles into a stationary equilibrium state after

t/M = 40. A spacetime diagram for the collapse is shown in Figure 8.17.

In Figure 8.18 the trajectories of four typical particles orbiting near the cluster center are

plotted. The simulation is performed with N

tot

= 7198 particles; at t/M = 0, a fraction

N/7198 of the total cluster rest-mass resides inside particle N . Particle 333, initially in

an elliptical-like orbit near r

/M = 1, moves along an inward spiral and is captured by

the black hole after two orbital periods. It illustrates the “avalanche-instability” whereby the

mass interior to this particle at pericenter grows sufﬁciently in two periods so that the

particle, initially outside the collapsing core, eventually ﬁnds itself on a capture orbit.

Particle 338 moves in a nearly elliptical orbit that extends out to r

/M = 1.5 and exhibits

large perhelion precession about the central hole. Pericenter for this particle is one of the

closest of all the ambient particles that do not get captured. It is located at r

/M = 0.25

or r

≈ 5. This result is consistent with the fact that particles which orbit a stationary

Schwarzschild black hole inside r

/M = 4 are inevitably captured.

It is also satisfying

that the pericenter position of this marginally stable orbit remains stationary with time,

further conﬁrming that, by the time the integrations terminate at t/M = 439, the cluster

achieves a new dynamic equilibrium about a stationary central black hole. Particle 340

moves nearly unperturbed in a circular orbit at r

/M = 1.

See, e.g., Misner et al. (1973).

288 Chapter 8 Spherically symmetric spacetimes

Figure 8.18 Orbital trajectories of four typical particles near the cluster center. In the top left panel the particle

is initially in an elliptical-like orbit, but spirals into the black hole after about two orbits. In the top right panel the

particle moves in a nearly elliptical orbit, exhibiting large perihelion precession about the central hole. In the

bottom left panel the particle moves essentially unperturbed in a nearly circular orbit. In the bottom right panel

the particle falls nearly radially into the black hole. [From Shapiro and Teukolsky (1988).]

Exercise 8.11 Interpret the behavior of particle 340 in light of Birkhoff’s theorem.

Particle 410 falls nearly radially from ≈ 7M into the black hole, illustrating how the

mass of the black hole grows beyond that of the collapsing core.

Finally, consider Figure 8.19 showing the fractional binding enery E

vs. central

redshift along an equilibrium sequence of n = 4 polytropes. The onset of instability as

determined by linear perturbation theory using trial functions (ω

< 0) occurs well beyond

the turning point. However, numerical integrations with the mean-ﬁeld, particle simulation

scheme show that all conﬁgurations beyond the ﬁrst turning point are dynamically unstable.

From this result and simulations involving other examples of parametrized sequences of

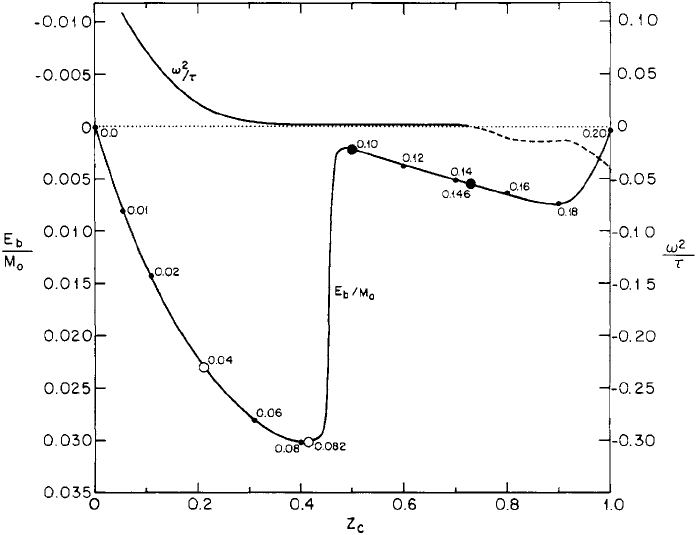
8.2 Collisionless clusters: stability and collapse 289

Figure 8.19 The fractional binding energy E

and oscillation frequency ω

in units of τ = ρ

∗

− P

are

plotted as functions of central redshift z

for the n = 4 polytropic sequence. Clusters along the sequence are

labeled by their value of the relativity parameter α as deﬁned in Fackerell (1970). The dynamical fates of four

models along the sequence, as determined by numerical simulation, are as follows: open large circles indicate

stable equilibrium; ﬁlled large circles indicate collapse to a black hole. [From Shapiro and Teukolsky (1985a).]

collisionless clusters, one concludes that the turning point on the binding energy curve

does signify the onset of dynamically instability, as in ﬂuid systems.

8.2.2 Phase space method

While the mean-ﬁeld, particle simulation scheme discussed in the previous section deter-

mines particle positions and velocities, it does not provide the phase space distribution

function f . As discussed in Chapter 5.3 a method to solve the relativistic Vlasov equation in

spherical symmetry directly for f by exploiting Liouville’s theorem has been developed.

The key idea for determining f is to implement equation (5.231). Knowing f determines

the matter source functions. The gravitational ﬁeld equations are the same as described

in the previous section. The virtue of the phase space method is that it accurately tracks the

Rasio et al. (1989b).

290 Chapter 8 Spherically symmetric spacetimes

increasingly complicated ﬁne-grained structure of the distribution function due to phase

mixing. For determining the global behavior of a collisionless system, the mean-ﬁeld

particle-simulation scheme is quite adequate. However, to obtain a detailed description of

the phase space distribution, especially when there is counter-streaming and phase mixing,

the direct phase space method is necessary.

Adopt the form for the line element given in equation (8.41). Again assume for simplicity

that the gas consists of a single species of mass m. As coordinates in phase space, choose

the radial velocity u

, the speciﬁc angular momentum j given by

j ≡

)

sin

, (8.82)

and the angle

ψ ≡ tan

−1





= tan

−1



sin θ



, (8.83)

measuring the orientation of the transverse velocity. Here the carets denote orthonormal

components. In spherical symmetry, f cannot depend on ψ,and j is a conserved quantity,

so that the Boltzmann equation (5.217) reduces to

∂ f

∂t





∂ f

∂r





∂ f

∂u

= 0 (8.84)

since ∂ f /∂ψ = 0anddj/dt = 0. Here we have taken f = f (t, x

, u

) ≡

dN/(d

), where d

= d

and where d

is given by equation (5.213).

Exercise 8.12 Show that for a spherical metric given by equation (8.41)(−g)

1/2

αr

sin θ and

αu

sin θ

αu

, (8.85)

where the integral over ψ has been carried out in the last expression.

In spherical symmetry, we can thus write f = f (t, r, u

, j). The coefﬁcients dr/dt and

/dt in equation (8.84) are given by geodesic equations (8.42) and (8.43). The ﬁeld

equations are unchanged from those described in the previous section. The matter source

terms are derived from f as in equations (5.207)–(5.210), using equation (5.213). For

example, the quantity ρ(t, r ) can be computed from

ρ = m



(αu

)

πm



∞



∞

−∞



1 +



1/2

. (8.86)

Note that one must be careful when evaluating the source terms at r = 0, where f = 0

only for j = 0. The coordinate singularity at r = 0 in these quadratures is eliminated by

recasting the d

in terms of velocity components in an orthonormal frame: d

(du

)/u

. The point r = 0 is the center of symmetry, in which case the distribution