Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

lattice mismatching effects. As shown by the experiments, within the last 1 or 2 nm, these effects can alter

the adhesive minima at a given separation by a factor of two. The force barriers, or maxima, may also depend

on orientation. This could be even more important than the effects on the minima. A high barrier could

prevent two surfaces from coming closer together into a much deeper adhesive well. Thus, the maxima can

effectively contribute to determining not only the ﬁnal separation of two surfaces, but also their ﬁnal adhesion.

Such considerations should be particularly important for determining the thickness and strength of inter-

granular spaces in ceramics, the adhesion forces between colloidal particles in concentrated electrolyte solu-

tions, and the forces between two surfaces in a crack containing capillary condensed water.

The intervening medium profoundly inﬂuences how one surface interacts with the other. As experi-

mental results show (McGuiggan and Israelachvili, 1990), when two surfaces are separated by as little as

0.4 nm of an amorphous material, such as adsorbed organics from air, then the surface granularity can

be completely masked and there is no mismatch effect on the adhesion. However, with another medium,

such as pure water which is presumably well ordered when conﬁned between two mica lattices, the atomic

granularity is apparent and alters the adhesion forces and whole interaction potential out to D > 1 nm.

Thus, it is not only the surface structure but also the liquid structure, or that of the intervening ﬁlm

material, which together determine the short-range interaction and adhesion.

On the other hand, for surfaces that are randomly rough, the oscillatory force becomes smoothed out

and disappears altogether, to be replaced by a purely monotonic solvation force. This occurs even if the

liquid molecules themselves are perfectly capable of ordering into layers. The situation of symmetric

liquid molecules conﬁned between rough surfaces is therefore not unlike that of asymmetric molecules

between smooth surfaces (see Figure 9.4).

To summarize some of the above points, for there to be an oscillatory solvation force, the liquid

molecules must be able to be correlated over a reasonably long range. This requires that both the liquid

molecules and the surfaces have a high degree of order or symmetry. If either is missing, so will the

oscillations. A roughness of only a few angstroms is often sufﬁcient to eliminate any oscillatory component

of a force law.

9.4.2 Effect of Surface Curvature and Geometry

It is easy to understand how oscillatory forces arise between two ﬂat, plane parallel surfaces (Figure 9.5).

Between two curved surfaces e.g., two spheres, one might imagine the molecular ordering and oscillatory

forces to be smeared out in the same way that they are smeared out between two randomly rough surfaces.

However, this is not the case. Ordering can occur so long as the curvature or roughness is itself regular

or uniform, i.e., not random. This interesting matter is due to the Derjaguin approximation, Equation 9.6,

which relates the force between two curved surfaces to the energy between two ﬂat surfaces. If the latter

is given by a decaying oscillatory function, as in Equation 9.15, then the energy between two curved

surfaces will simply be the integral of that function, and since the integral of a cosine function is another

cosine function, with some appropriate phase shift, we see why periodic oscillations will not be smeared

out simply by changing the surface curvature. Likewise, two surfaces with regularly curved regions will

also retain their oscillatory force proﬁle, albeit modiﬁed, so long as the corrugations are truly regular, i.e.,

periodic. On the other hand, surface roughness, even on the nanometer scale, can smear out any

oscillations if the roughness is random and the liquid molecules are smaller than the size of the surface

asperities.

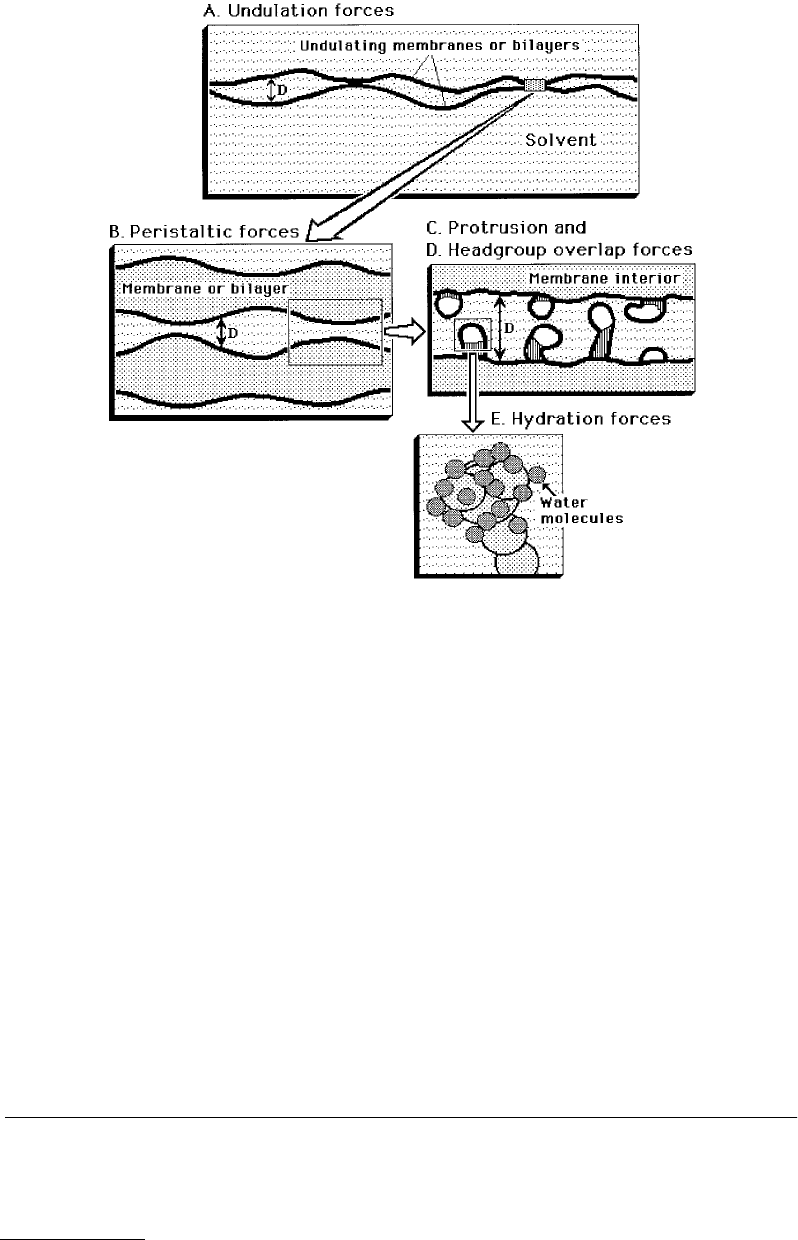
9.5 Thermal Fluctuation Forces: Forces between Soft,

Fluidlike Surfaces

If a surface or interface is not rigid but very soft or even ﬂuidlike, this can act to smear out any oscillatory

solvation force. This is because the thermal ﬂuctuations of such interfaces make them dynamically “rough”

at any instant, even though they may be perfectly smooth on a time average. The types of surfaces that

fall into this category are ﬂuidlike amphiphilic surfaces of micelles, bilayers, emulsions, soap ﬁlms, etc.,

but also solid colloidal particle surfaces that are coated with surfactant monolayers, as occur in lubricating

oils, paints, toners, etc.

Thermal ﬂuctuation forces are usually of short range and repulsive, and are very effective at stabilizing

the attractive van der Waals forces at some small but ﬁnite separation which can reduce the adhesion

energy or force by up to three orders of magnitude. It is mainly for this reason that ﬂuidlike micelles

and bilayers, biological membranes, emulsion droplets (in salad dressings), or gas bubbles (in beer)

adhere to each other only very weakly (Figure 9.6).

Because of their short range, it was, and still is, commonly believed that these forces arise from water

ordering or “structuring” effects at surfaces, and that they reﬂect some unique or characteristic property

of water (see Section 9.6). However, it is now known that these repulsive forces also exist in other liquids.

Moreover, they appear to become stronger with increasing temperature, which is unlikely for a force that

originates from molecular ordering effects at surfaces. Recent experiments, theory, and computer simu-

lations (Israelachvili and Wennerström, 1990, 1996; Granfeldt and Miklavic, 1991)

have shown that these

repulsive forces have an entropic origin — arising from the osmotic repulsion between exposed thermally

mobile surface groups once these overlap in a liquid.

9.6 Hydration Forces: Special Forces in Water

and Aqueous Solutions

9.6.1 Repulsive Hydration Forces

The forces occurring in water and electrolyte solutions are more complex than those occurring in

nonpolar liquids. According to continuum theories, the attractive van der Waals force is always expected

FIGURE 9.6 The four most common types of thermal ﬂuctuation forces (also referred to as steric or entropic forces)

between ﬂuid-like, usually amphiphilic, surfaces and membranes in liquids.

to win over the repulsive electrostatic double-layer force at small surface separations (Figure 9.3). How-

ever, certain surfaces (usually oxide or hydroxide surfaces such as clays and silica) swell spontaneously

or repel each other in aqueous solutions even in very high salt. Yet in all these systems one would expect

the surfaces or particles to remain in strong adhesive contact or coagulate in a primary minimum if the

only forces operating were DLVO forces.

There are many other aqueous systems where DLVO theory fails and where there is an additional

short-range force that is not oscillatory but smoothly varying, i.e., monotonic. Between hydrophilic

surfaces this force is exponentially repulsive and is commonly referred to as the hydration or structural

force. The origin and nature of this force has long been controversial especially in the colloidal and

biological literature. Repulsive hydration forces are believed to arise from strongly H-bonding surface

groups, such as hydrated ions or hydroxyl (–OH) groups, which modify the H-bonding network of liquid

water adjacent to them. Since this network is quite extensive in range (Stanley and Teixeira, 1980), the

resulting interaction force is also of relatively long range.

Repulsive hydration forces were ﬁrst extensively studied between clay surfaces (van Olphen, 1977).

More recently they have been measured in detail between mica and silica surfaces (Pashley, 1981, 1982,

1985; Horn et al., 1989b) where they have been found to decay exponentially with decay lengths of about

1 nm. Their effective range is about 3 to 5 nm, which is about twice the range of the oscillatory solvation

force in water. Empirically, the hydration repulsion between two hydrophilic surfaces appears to follow

the simple equation (over a limited range)

(9.16)

where λ

≈ 0.6 — 1.1 nm for 1:1 electrolytes, and where E

= 3 to 30 mJ m

–2

depending on the hydration

(hydrophilicity) of the surfaces, higher E

values generally being associated with lower λ

values.

In a series of experiments to identify the factors that regulate hydration forces, Pashley (1981, 1982,

1985) found that the interaction between molecularly smooth mica surfaces in dilute electrolyte solutions

obeys the DLVO theory. However, at higher salt concentrations, speciﬁc to each electrolyte, hydrated

cations bind to the negatively charged surfaces and give rise to a repulsive hydration force (Figure 9.7).

This is believed to be due to the energy needed to dehydrate the bound cations, which presumably retain

some of their water of hydration on binding. This conclusion was arrived at after noting that the strength

and range of the hydration forces increase with the known hydration numbers of the electrolyte cations

in the order: Mg

> Ca

> Li

~ Na

> K

> Cs

. Similar trends are observed with other negatively

charged colloidal surfaces.

While the hydration force between two mica surfaces is overall repulsive below about 4 nm, it is not

always monotonic below about 1.5 nm but exhibits oscillations of mean periodicity 0.25 ± 0.03 nm,

roughly equal to the diameter of the water molecule. This is shown in Figure 9.7, where we may note

that the ﬁrst three minima at D ≈ 0, 0.28, and 0.56 nm occur at negative energies, a result that rationalizes

observations on certain colloidal systems. For example, clay platelets such as motmorillonite often repel

each other increasingly strongly as they come closer together, but they are also known to stack into stable

aggregates with water interlayers of typical thickness 0.25 and 0.55 nm between them (Del Pennino et al.,

1981; Viani et al., 1984), suggestive of a turnaround in the force law from a monotonic repulsion to

discretized attraction. In chemistry we would refer to such structures as stable hydrates of ﬁxed stochi-

ometry, while in physics we may think of them as experiencing an oscillatory force.

Both surface force and clay-swelling experiments have shown that hydration forces can be modiﬁed

or “regulated” by exchanging ions of different hydrations on surfaces, an effect that has important practical

applications in controlling the stability of colloidal dispersions. It has long been known that colloidal

particles can be precipitated (coagulated or ﬂocculated) by increasing the electrolyte concentration —

an effect that was traditionally attributed to the reduced screening of the electrostatic double-layer

repulsion between the particles due to the reduced Debye length. However, there are many examples

where colloids become stable — not at lower salt concentrations — but at high concentrations. This

effect is now recognized as being due to the increased hydration repulsion experienced by certain surfaces

EEe

−

when they bind highly hydrated ions at higher salt concentrations. “Hydration regulation” of adhesion

and interparticle forces is an important practical method for controlling various processes such as clay

swelling (Quirk, 1968; Del Pennino et al., 1981; Viani et al., 1983), ceramic processing and rheology

(Horn, 1990; Velamakanni et al., 1990), material fracture (Horn, 1990), and colloidal particle and bubble

coalescence (Lessard and Zieminski, 1971; Elimelech, 1990).

9.6.2 Attractive Hydrophobic Forces

Water appears to be unique in having a solvation (hydration) force that exhibits both a monotonic and

an oscillatory component. Between hydrophilic surfaces the monotonic component is repulsive

(Figure 9.7), but between hydrophobic surfaces it is attractive and the ﬁnal adhesion in water is much

greater than expected from the Lifshitz theory.

A hydrophobic surface is one that is inert to water in the sense that it cannot bind to water molecules

via ionic or hydrogen bonds. Hydrocarbons and ﬂuorocarbons are hydrophobic, as is air, and the strongly

attractive hydrophobic force has many important manifestations and consequences, some of which are

illustrated in Figure 9.8.

In recent years there has been a steady accumulation of experimental data on the force laws between

various hydrophobic surfaces in aqueous solutions. These surfaces include mica surfaces coated with

surfactant monolayers exposing hydrocarbon or ﬂuorocarbon groups, or silica and mica surfaces that

had been rendered hydrophobic by chemical methylation or plasma etching (Israelachvili and Pashley,

1982; Pashley et al., 1985; Claesson et al., 1986; Claesson and Christenson, 1988; Rabinowich and Der-

jaguin, 1988; Parker et al., 1989; Christenson et al., 1990; Kurihara et al., 1990). These studies have found

that the hydrophobic force law between two macroscopic surfaces is of surprisingly long range, decaying

exponentially with a characteristic decay length of 1 to 2 nm in the range 0 to 10 nm, and then more

FIGURE 9.7 Measured forces between charged mica surfaces in various dilute and concentrated KCl solutions. In

dilute solutions (10

–5

and 10

–4

M) the repulsion reaches a maximum and the surfaces jump into molecular contact

from the tops of the force barriers (see also Figure 9.3). In dilute solutions the measured forces are excellently described

by the DLVO theory, based on exact numerical solutions to the nonlinear Poisson–Boltzmann equation for the

electrostatic forces and the Lifshitz theory for the van der Waals forces (using a Hamaker constant of A = 2.2 ×

–20

J). At higher electrolyte concentrations, as more hydrated K

cations adsorb onto the negatively charged surfaces,

an additional hydration force appears superimposed on the DLVO interaction. This has both an oscillatory and a

monotonic component. Inset: Short-range hydration forces between mica surfaces plotted as pressure against distance.

Lower curve: force measured in dilute 1 mM KCl solution where there is one K

ion adsorbed per 1.0 nm

(surfaces

40% saturated with K

ions). Upper curve: force measured in 1 M KCl where there is one K

ion adsorbed per

0.5 nm

(surfaces 95% saturated with adsorbed cations). At larger separations the forces are in good agreement with

the DLVO theory. The right-hand ordinate gives the corresponding interaction energy according to Equation 9.6.

gradually farther out. The hydrophobic force can be far stronger than the van der Waals attraction,

especially between hydrocarbon surfaces for which the Hamaker constant is quite small.

As might be expected, the magnitude of the hydrophobic attraction falls with the decreasing hydro-

phobicity (increasing hydrophilicity) of surfaces. Helm et al. (1989) measured the forces between

uncharged but hydrated lecithin bilayers in water as a function of increasing hydrophobicity of the bilayer

surfaces. This was achieved by progressively increasing the head group area per amphiphilic molecule

exposed to the aqueous phase, i.e., by progressively exposing more of the hydrocarbon chains. The results

showed that with increasing hydrophobic area the forces became progressively more attractive at longer

range, that the adhesion increased, and that the stabilizing repulsive short-range hydration forces

decreased. This shows how the overall force curve changes as an initially hydrophilic surface becomes

progressively more hydrophobic.

For two surfaces in water their purely hydrophobic interaction energy (i.e., ignoring DLVO and

oscillatory forces) in the range 0 to 10 nm is given by

(9.17)

where, typically, λ

= 1 to 2 nm, and γ

= 10 to 50 mJ m

–2

, where the higher value corresponds to the

interfacial energy of a pure hydrocarbon–water interface.

At a separation below 10 nm the hydrophobic force appears to be insensitive or only weakly sensitive

to changes in the type and concentration of electrolyte ions in the solution. The absence of a “screening”

effect by ions attests to the nonelectrostatic origin of this interaction. In contrast, some experiments have

shown that at separations greater than 10 nm the attraction does depend on the intervening electrolyte,

and that in dilute solutions, or solutions containing divalent ions, it can continue to exceed the van der

Waals attraction out to separations of 80 nm (Christenson et al., 1989, 1990).

The long-range nature of the hydrophobic interaction has a number of important consequences. It

accounts for the rapid coagulation of hydrophobic particles in water, and may also account for the rapid

folding of proteins. It also explains the ease with which water ﬁlms rupture on hydrophobic surfaces. In

this, the van der Waals force across the water ﬁlm is repulsive and therefore favors wetting, but this is

more than offset by the attractive hydrophobic interaction acting between the two hydrophobic phases

across water. Finally, hydrophobic forces are increasingly being implicated in the adhesion and fusion of

biological membranes and cells. It is known that both osmotic and electric ﬁeld stresses enhance mem-

brane fusion, an effect that may be due to the increase in the hydrophobic area exposed between two

adjacent surfaces.

FIGURE 9.8 Examples of attractive hydrophobic interactions in

aqueous solutions. (a) Low solubility/immiscibility of water and oil

molecules; (b) micellization; (c) dimerization and association of

hydrocarbon chains in water; (d) protein folding; (e) strong adhe-

sion of hydrophobic surfaces; (f) nonwetting of water on hydro-

phobic surfaces; (g) rapid coagulation of hydrophobic or

surfactant-coated surfaces; (h) hydrophobic particle attachment to

rising air bubbles (basic mechanism of “froth ﬂotation” process

used to separate hydrophobic and hydrophilic minerals).

=−

−

9.6.3 Origin of Hydration Forces

From the previous discussions we can infer that hydration forces are not of a simple nature, and it may

be fair to say that this interaction is probably the most important yet the least understood of all the forces

in liquids. Clearly, the very unusual properties of water are implicated, but the nature of the surfaces is

equally important. Some particle surfaces can have their hydration forces regulated, for example, by ion

exchange. Other surfaces appear to be intrinsically hydrophilic (e.g., silica) and cannot be coagulated by

changing the ionic conditions. However, such surfaces can often be rendered hydrophobic by chemically

modifying their surface groups. For example, on heating silica to above 600°C, two surface silanol –OH

groups release a water molecule and combine to form a hydrophobic siloxane –O– group, whence the

repulsive hydration force changes into an attractive hydrophobic force.

How do these exponentially decaying repulsive or attractive forces arise? Theoretical work and com-

puter simulations (Christou et al., 1981; Jönsson, 1981; Kjellander and Marcelja, 1985a,b; Henderson

and Lozada-Cassou, 1986) suggest that the solvation forces in water should be purely oscillatory, while

other theoretical studies (Marcelja and Radic, 1976; Marcelja et al., 1977; Gruen and Marcelja, 1983;

Jönsson and Wennerström, 1983; Schiby and Ruckenstein, 1983; Luzar et al., 1987; Attard and Batchelor,

1988; Marcelja, 1997) suggest a monotonic exponential repulsion or attraction, possibly superimposed

on an oscillatory proﬁle. The latter is consistent with experimental ﬁndings, as shown in the inset to

Figure 9.7, where it appears that the oscillatory force is simply additive with the monotonic hydration

and DLVO forces, suggesting that these arise from essentially different mechanisms.

It is probable that the intrinsic hydration force between all smooth, rigid, or crystalline surfaces (e.g.,

mineral surfaces such as mica) has an oscillatory component. This may or may not be superimposed on a

monotonic repulsion (Figure 9.9) due to image interactions (Jönsson and Wennerström, 1983), structural

or H-bonding interactions (Marcelja and Radic, 1976; Marcelja et al., 1977; Gruen and Marcelja, 1983) or —

as now seems more likely — steric and entropic forces (Israelachvili and Wennerström, 1996; Marcelja, 1997).

Like the repulsive hydration force, the origin of the hydrophobic force is still unknown. Luzar et al.

(1987) carried out a Monte Carlo simulation of the interaction between two hydrophobic surfaces across

water at separations below 1.5 nm. They obtained a decaying oscillatory force superimposed on a mono-

tonically attractive curve, i.e., similar to Figure 9.9.

It is questionable whether the hydration or hydrophobic force should be viewed as an ordinary type

of solvation or structural force — simply reﬂecting the packing of the water molecules. It is important

FIGURE 9.9 Typical short-range solvation (hydration)

forces in water as a function of distance, D, normalized by the

diameter of the water molecule, σ (about 0.25 nm). The hydra-

tion forces in water differ from those in other liquids in that

there is a monotonic component in addition to the normal

purely oscillatory component. For hydrophilic surfaces the

monotonic component is repulsive (upper dashed curve),

whereas for hydrophobic surfaces it is attractive (lower dashed

curve). For simpler liquids there are no such monotonic com-

ponents, and both theory and experiments show that the oscil-

lations decay with distance with the maxima and minima,

respectively, above and below the baseline of the van der Waals

force (middle dashed curve) or superimposed on the contin-

uum DLVO interaction.

to note that for any given positional arrangement of water molecules, whether in the liquid or solid state,

there is an almost inﬁnite variety of ways the H-bonds can be interconnected over three-dimensional

space while satisfying the Bernal–Fowler rules requiring two donors and two acceptors per water molecule.

In other words, the H-bonding structure is actually quite distinct from the molecular structure. The

energy (or entropy) associated with the H-bonding network, which extends over a much larger region

of space than the molecular correlations, is probably at the root of the long-range solvation interactions

of water. But whatever the answer, it is clear that the situation in water is governed by much more than

the simple molecular-packing effects that seem to dominate the interactions in simpler liquids.

9.7 Adhesion and Capillary Forces

When considering the adhesion of two solid surfaces or particles in air or in a liquid, it is easy to overlook

or underestimate the important role of capillary forces, i.e., forces arising from the Laplace pressure of

curved menisci which have formed as a consequence of the condensation of a liquid between and around

two adhering surfaces (Figure 9.10).

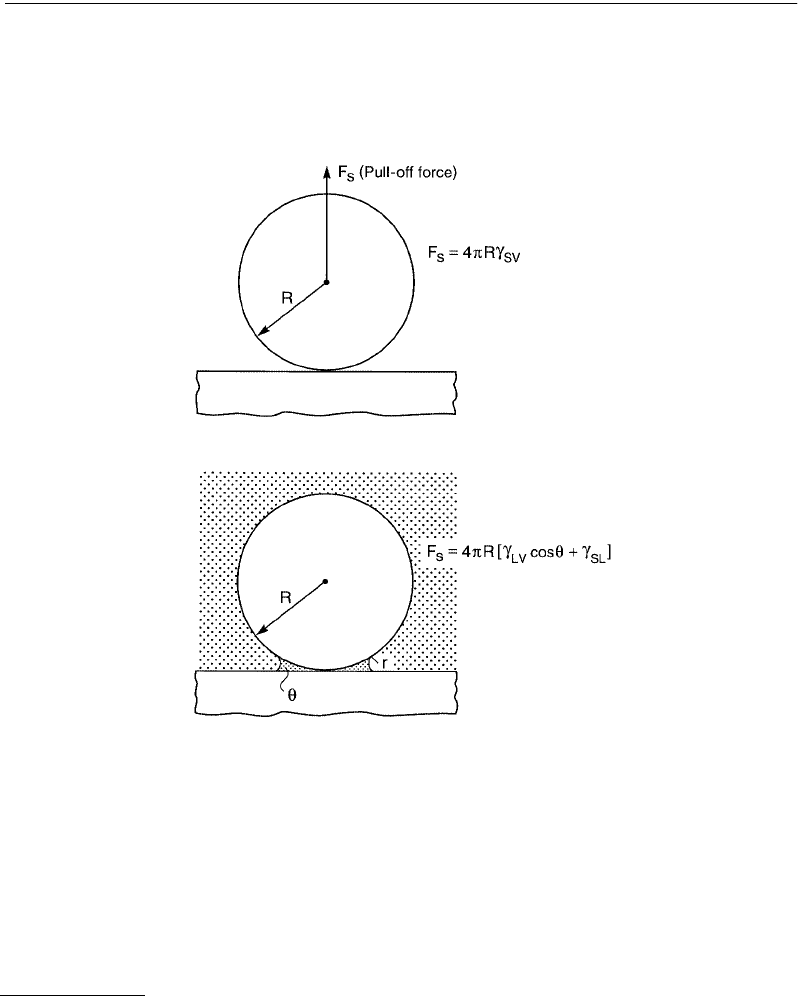
FIGURE 9.10 Sphere on ﬂat in an inert atmosphere (top), and in an atmosphere containing vapor that can “capillary

condense” around the contact zone (bottom). At equilibrium the concave radius, r, of the liquid meniscus is given

by the Kelvin equation. The radius r increases with the relative vapor pressure, but for condensation to occur the

contact angle θ must be less than 90° or else a concave meniscus cannot form. The presence of capillary condensed

liquid changes the adhesion force, as given by Equations 9.18 and 9.19. Note that this change is independent of r so

long as the surfaces are perfectly smooth. Experimentally, it is found that for simple inert liquids such as cyclohexane,

these equations are valid already at Kelvin radii as small as 1 nm — about the size of the molecules themselves.

Capillary condensation also occurs in binary liquid systems e.g., when small amounts of water dissolved in hydro-

carbon liquids condense around two contacting hydrophilic surfaces, or when a vapor cavity forms in water around

two hydrophobic surfaces.

The adhesion force between a spherical particle of radius R and a ﬂat surface in an inert atmosphere is

(9.18)

but in an atmosphere containing a condensable vapor, the above becomes replaced by

(9.19)

where the ﬁrst term is due to the Laplace pressure of the meniscus and the second is due to the direct

adhesion of the two contacting solids within the liquid. Note that the above equation does not contain

the radius of curvature, r, of the liquid meniscus (Figure 9.10). This is because for smaller r the Laplace

pressure

/r increases, but the area over which it acts decreases by the same amount, so the two effects

cancel out. A natural question arises as to the smallest value of r for which Equation 9.19 will apply.

Experiments with inert liquids, such as hydrocarbons, condensing between two mica surfaces indicate

that Equation 9.19 is valid for values of r as small as 1 to 2 nm, corresponding to vapor pressures as low

as 40% of saturation (Fisher and Israelachvili, 1981; Christenson, 1988b). With water condensing from

vapor or from oil it appears that the bulk value of

is also applicable for meniscus radii as small as 2 nm.

The capillary condensation of liquids, especially water, from vapor can have additional effects on the

whole physical state of the contact zone. For example, if the surfaces contain ions, these will diffuse and

build up within the liquid bridge, thereby changing the chemical composition of the contact zone as well

as inﬂuencing the adhesion. More dramatic effects can occur with amphiphilic surfaces, i.e., those

containing surfactant or polymer molecules. In dry air, such surfaces are usually nonpolar — exposing

hydrophobic groups such as hydrocarbon chains. On exposure to humid air, the molecules can overturn

so that the surface nonpolar groups become replaced by polar groups, which renders the surfaces

hydrophilic. When two such surfaces come into contact, water will condense around the contact zone

and the adhesion force will also be affected — generally increasing well above the value expected for inert

hydrophobic surfaces.

It is clear that the adhesion of two surfaces in vapor or a solvent can often be largely determined by

capillary forces arising from the condensation of liquid that may be present only in very small quantities

e.g., 10 to 20% of saturation in the vapor, or 20 ppm in the solvent.

9.7.1 Adhesion Mechanics

Modern theories of the adhesion mechanics of two contacting solid surfaces are based on the

Johnson–Kendall–Roberts (JKR) theory (Johnson et al., 1971, Pollock et al., 1978; Barquins and Maugis,

1982). In the JKR theory two spheres of radii R

and R

, bulk elastic moduli K, and surface energy γ per

unit area will ﬂatten when in contact. The contact area will increase under an external load or force F,

such that at mechanical equilibrium the contact radius r is given by

(9.20)

where R = R

/(R

+ R

). Another important result of the JKR theory gives the adhesion force or pull

off force:

(9.21)

where, by deﬁnition, the surface energy γ

, is related to the reversible work of adhesion W, by W = 2γ

Note that according to the JKR theory a ﬁnite elastic modulus, K, while having an effect on the load–area

ssv

=π4 γ ,

sLVSL

=π +

()

4 γθγcos ,

FR RF R

612 6=+π+π+π

()













γγγ,

=− π3 γ ,

curve, has no effect on the adhesion force — an interesting and unexpected result that has nevertheless

been veriﬁed experimentally (Johnson et al., 1971; Israelachvili, 1991).

Equations 9.20 and 9.21 are the basic equations of the JKR theory and provide the framework for

analyzing the results of adhesion measurements of contacting solids, known as contact mechanics (Pollock

et al., 1978; Barquins and Maugis, 1982), and for studying the effects of surface conditions and time on

adhesion energy hysteresis (see next section).

9.8 Nonequilibrium Interactions: Adhesion Hysteresis

Under ideal conditions the adhesion energy is a well-deﬁned thermodynamic quantity. It is normally

denoted by E or W (the work of adhesion) or γ (the surface tension, where W = 2γ), and it gives the

reversible work done on bringing two surfaces together or the work needed to separate two surfaces from

contact. Under ideal, equilibrium conditions these two quantities are the same, but under most realistic

conditions they are not: the work needed to separate two surfaces is always greater than that originally

gained on bringing them together. An understanding of the molecular mechanisms underlying this

phenomenon is essential for understanding many adhesion phenomena, energy dissipation during load-

ing–unloading cycles, contact angle hysteresis, and the molecular mechanisms associated with many

frictional processes. It is wrong to think that hysteresis arises because of some imperfection in the system,

such as rough or chemically heterogeneous surfaces, or because the supporting material is viscoelastic;

adhesion hysteresis can arise even between perfectly smooth and chemically homogeneous surfaces

supported by perfectly elastic materials, and can be responsible for such phenomena as “rolling” friction

and elastoplastic adhesive contacts (Bowden and Tabor, 1967; Greenwood and Johnson, 1981; Maugis,

1985; Michel and Shanahan, 1990) during loading–unloading and adhesion–decohesion cycles.

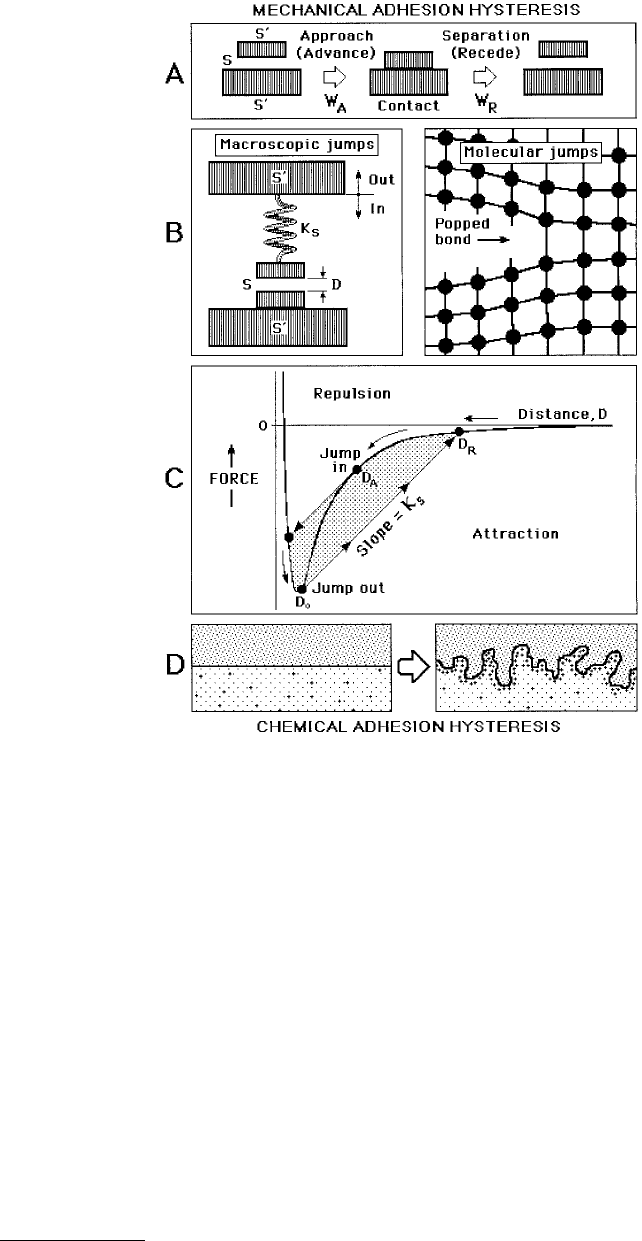
Adhesion hysteresis may be thought of as being due to mechanical or chemical effects, as illustrated

in Figure 9.11. In general, if the energy change, or work done, on separating two surfaces from adhesive

contact is not fully recoverable on bringing the two surfaces back into contact again, the adhesion

hysteresis may be expressed as

(9.22)

where W

and W

are the adhesion or surface energies for receding (separating) and advancing (approach-

ing) two solid surfaces, respectively. Figure 9.12 shows the results of a typical experiment that measures

the adhesion hysteresis between two surfaces (Chaudhury and Whitesides, 1991; Chen et al., 1991). In

this case, two identical surfactant-coated mica surfaces were used in an SFA. By measuring the contact

radius as a function of applied load both for increasing and decreasing loads two different curves are

obtained. These can be ﬁtted to the JKR equation, Equation 9.20, to obtain the advancing (loading) and

receding (unloading) surface energies.

Hysteresis effects are also commonly observed in wetting/dewetting phenomena (Miller and Neogi,

1985). For example, when a liquid spreads and then retracts from a surface the advancing contact angle

is generally larger than the receding angle θ

. Since the contact angle, θ, is related to the liquid–vapor

surface tension, γ, and the solid–liquid adhesion energy, W, by the Dupré equation:

(9.23)

we see that wetting hysteresis or contact angle hysteresis (θ

> θ

) actually implies adhesion hysteresis,

> W

, as given by Equation 9.22.

Receding Advancing

∆WWW

=−

()

> 0,

()

=cos ,θγ

Energy dissipating processes such as adhesion and contact angle hysteresis arise because of practical

constraints of the ﬁnite time of measurements and the ﬁnite elasticity of materials which prevent many

loading–unloading or approach–separation cycles to be thermodynamically irreversible, even though if

these were carried out inﬁnitely slowly they would be. By thermodynamic irreversibly one simply means

that one cannot go through the approach–separation cycle via a continuous series of equilibrium states

FIGURE 9.11 Origin of adhesion hysteresis during the approach and separation of two solid surfaces. (A) In all

realistic situations the force between two solid surfaces is never measured at the surfaces themselves, S, but at some

other point, say S´, to which the force is elastically transmitted via the backing material supporting the surfaces.

(B, left) “Magnet” analogy of how mechanical adhesion hysteresis arises for two approaching or separating surfaces,

where the lower is ﬁxed and where the other is supported at the end of a spring of stiffness K

. (B, right) On the

molecular or atomic level, the separation of two surfaces is accompanied by the spontaneous breaking of bonds,

which is analogous to the jump apart of two macroscopic surfaces or magnets. (C) Force–distance curve for two

surfaces interacting via an attractive van der Waals–type force law, showing the path taken by the upper surface on

approach and separation. On approach, an instability occurs at D = D

, where the surfaces spontaneously jump into

contact at D ≈ D

. On separation, another instability occurs where the surfaces jump apart from ~D

to D

(D) Chemical adhesion hysteresis produced by interdiffusion, interdigitation, molecular reorientations and exchange

processes occurring at an interface after contact. This induces roughness and chemical heterogeneity even though

initially (and after separation and reequilibration) both surfaces are perfectly smooth and chemically homogeneous.