Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

bound octadecyl phosphonic acid monolayer on alumina surfaces is shown in Figure 9.20. In this case,

the friction is higher than untreated undamaged α-alumina surfaces, but the bare surfaces easily damage

upon sliding, resulting in an ultimately higher friction system with greater wear rates than the more

robust monolayer-coated surfaces.

Clearly, the mechanism and factors that determine normal friction are quite different from those that

govern interfacial friction. These mechanisms are described in the theoretical section below, but one

should point out that this effect is not general and may only apply to brittle materials. For example, the

friction of ductile surfaces is totally different and involves the continuous plastic deformation of con-

tacting surface asperities during sliding rather than the rolling of two surfaces on hard wear particles

(Bowden and Tabor, 1967). Furthermore, in the case of ductile surfaces, water and other surface-active

components do have an effect on the friction coefﬁcients under normal sliding conditions.

9.11 Theories of Interfacial Friction

9.11.1 Theoretical Modeling of Interfacial Friction: Molecular Tribology

The following friction model, ﬁrst proposed by Tabor (1982) and developed further by Sutcliffe et al.

(1978), McClelland (1989), and Homola et al. (1989), has been quite successful at explaining the inter-

facial and boundary friction of two solid crystalline surfaces sliding past each other in the absence of

wear. The surfaces may be unlubricated, or they may be separated by a monolayer or more of some

boundary lubricant or liquid molecules. In this model, the values of the critical shear stress S

, and the

coefﬁcient of friction µ, of Equation 9.27 are calculated in terms of the energy needed to overcome the

attractive intermolecular forces and compressive externally applied load as one surface is raised and then

slid across the molecular-sized asperities of the other.

This model (variously referred to as the interlocking asperity model, coulomb friction,

or the cobblestone

model) is akin to pushing a cart over a road of cobblestones where the cartwheels (which represent the

molecules of the upper surface or ﬁlm) must be made to roll over the cobblestones (representing the

molecules of the lower surface) before the cart can move. In the case of the cart, the downward force of

gravity replaces the attractive intermolecular forces between two material surfaces. When at rest the

cartwheels ﬁnd grooves between the cobblestones where they sit in potential energy minima and so the

cart is at some stable mechanical equilibrium. A certain lateral force (the “push”) is required to raise the

cartwheels against the force of gravity in order to initiate motion. Motion will continue as long as the

cart is pushed, and rapidly stops once it is no longer pushed. Energy is dissipated by the liberation of

heat (phonons, acoustic waves, etc.) every time a wheel hits the next cobblestone. The cobblestone model

is not unlike the old coulomb and interlocking asperity models of friction (Dowson, 1979) except that

it is being applied at the molecular level and where the external load is augmented by attractive inter-

molecular forces.

There are thus two contributions to the force pulling two surfaces together: the externally applied load

or pressure, and the (internal) attractive intermolecular forces which determine the adhesion between

the two surfaces. Each of these contributions affects the friction force in a different way, and we start by

considering the role of the internal adhesion forces.

9.11.2 Adhesion Force Contribution to Interfacial Friction

Consider the case of two surfaces sliding past each other as shown in Figure 9.21. When the two surfaces

are initially in adhesive contact, the surface molecules will adjust themselves to ﬁt snugly together, in an

analogous manner to the self-positioning of the cartwheels on the cobblestone road. A small tangential

force applied to one surface will therefore not result in the sliding of that surface relative to the other.

The attractive van der Waals forces between the surfaces must ﬁrst be overcome by having the surfaces

separate by a small amount. To initiate motion, let the separation between the two surfaces increase by

a small amount ∆D, while the lateral distance moved is ∆d. These two values will be related via the

geometry of the two surface lattices. The energy put into the system by the force F acting over a lateral

distance ∆d is

(9.30)

This energy may be equated with the change in interfacial or surface energy associated with separating

the surfaces by ∆D, i.e., from the equilibrium separation D = D

to D = (D

+∆D). Since γ ∝ D

–2

, the

surface energy cost may be approximated by

(9.31)

where γ is the surface energy, A the contact area, and where D

is the surface separation at equilibrium.

During steady-state sliding (kinetic friction), not all of this energy will be lost or absorbed by the lattice

every time the surface molecules move by one lattice spacing: some fraction will be reﬂected during each

impact of the cartwheel molecules (McClelland, 1989). Assuming that a fraction ε of the above surface

energy is lost every time the surfaces move across the characteristic length ∆d (Figure 9.21), we obtain

after equating the above two equations

(9.32)

For a typical hydrocarbon or a van der Waals surface, γ ≈ 25 × 10

–3

J/m

. Other typical values would be

∆D ≈ 0.5 Å, D

≈ 2 Å, ∆d ≈ 1 Å, and ε ≈ 0.1 to 0.5. By using the above parameters, Equation 9.32 predicts

≈ (2.5 to 12.5) × 10

N/m

for van der Waals surfaces. This range of values compares very well with

typical experimental values of 2 × 10

N/m

for hydrocarbon or mica surfaces sliding in air or separated

by one molecular layer of cyclohexane (Homola et al., 1989).

The above model may be extended, at least semiquantitatively, to lubricated sliding, where a thin liquid

ﬁlm is present between the surfaces. With an increase in the number of liquid layers between the surfaces,

increases while ∆D decreases, hence the lower the friction force. This is precisely what is observed.

But with more than one liquid layer between two surfaces, the situation becomes too complex to analyze

FIGURE 9.21 Schematic illustration of how one molecularly smooth surface moves over another when a lateral

force F is applied. As the upper surface moves laterally by some fraction of the lattice dimension ∆d, it must also

move up by some fraction of an atomic or molecular dimension ∆D, before it can slide across the lower surface. On

impact, some fraction ε of the kinetic energy is “transmitted” to the lower surface, the rest being “reﬂected” back to

the colliding molecule (upper surface).

Input energy: .Fd×∆

Surface energy change: ,21 4

γγADDD ADD−+

()













≈

()

∆∆

⋅

γε ∆

∆

analytically (actually, even with one or no interfacial layers, the calculation of the fraction of energy

dissipated per molecular collision ε is not a simple matter). Sophisticated modeling based on computer

simulations is now required, as described in the following section.

9.11.3 Relation between Boundary Friction

and Adhesion Energy Hysteresis

While the above equations suggest that there is a direct correlation between friction and adhesion, this

is not the case. The correlation is really between friction and adhesion hysteresis, described in Section 9.8.

In the case of friction, this subtle point is hidden in the factor ε, which is a measure of the amount of

energy absorbed (dissipated, transferred, or lost) by the lower surfaces when it is impacted by a molecule

from the upper surface. If ε = 0, all the energy is reﬂected and there will be no kinetic friction force, nor

any adhesion hysteresis, but the absolute magnitude of the adhesion force or energy would remain ﬁnite

and unchanged. This is illustrated in Figure 9.22.

The following simple model shows how adhesion hysteresis and friction may be quantitatively related.

Let ∆γ = (γ

to γ

) be the adhesion energy hysteresis per unit area, as measured during a typical load-

ing–unloading cycle (see Figure 9.22C and D). Now consider the same two surfaces sliding past each

other and assume that frictional energy dissipation occurs through the same mechanism as adhesion

energy dissipation, and that both occur over the same characteristic molecular length scale σ. Thus, when

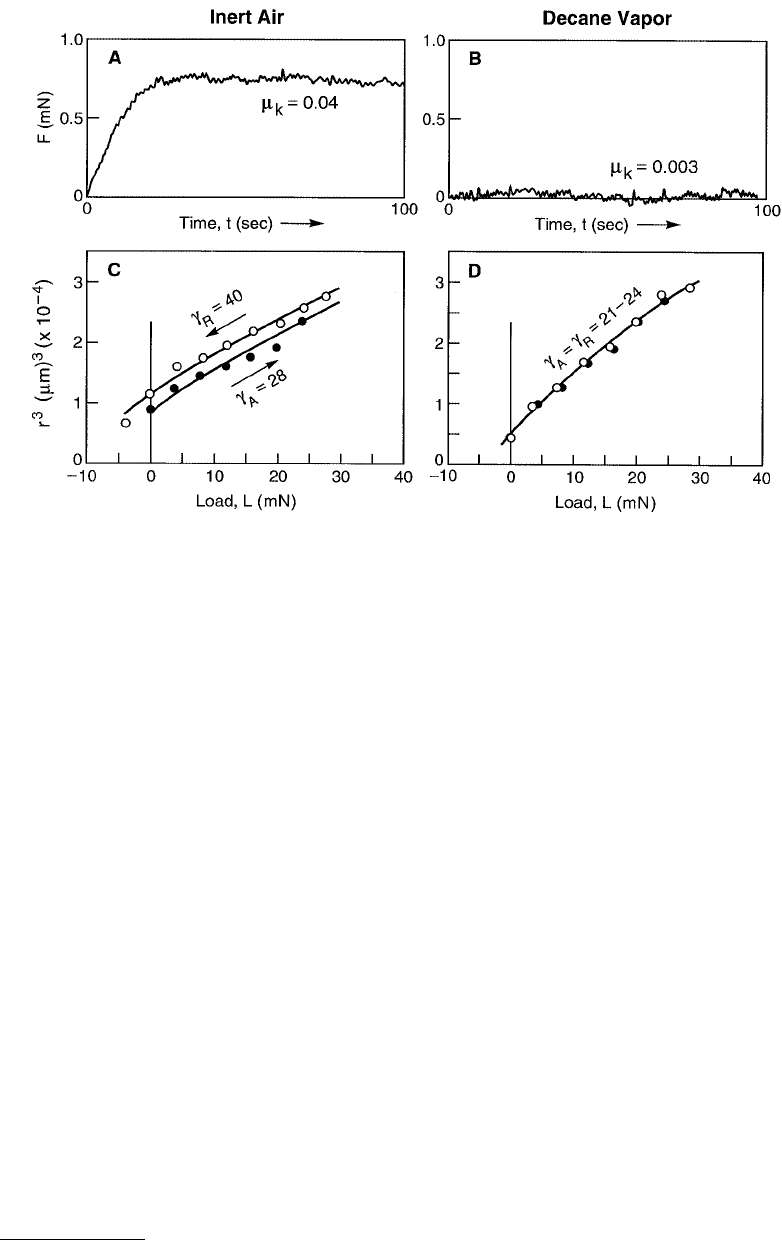
FIGURE 9.22 Top: Friction traces for two ﬂuid-like monolayer-coated surfaces at 25° C showing that the friction

force is much higher between dry monolayers (A) than between monolayers whose ﬂuidity has been enhanced by

hydrocarbon penetration from vapor (B). (From Chen et al., 1991.) Bottom: Contact radius vs. load (r

–L) curves

measured for the same two surfaces as above and ﬁtted to the JKR equation (Equation 9.20 — shown by the solid

lines. For dry monolayers (C) the adhesion energy on unloading (γ

= 40 mJ/m

) is greater than that on loading

(γ

= 28 mJ/m

), indicative of an adhesion energy hysteresis of ∆γ = γ

– γ

= 12 mJ/m

. For monolayers exposed to

saturated decane vapor (D) their adhesion hysteresis is zero (γ

= γ

), and both the loading and unloading curves

are well ﬁtted by the thermodynamic value of the surface energy of ﬂuid hydrocarbon chains, γ ≈ 24 mJ/m

the two surfaces (of contact area A = πr

) move a distance σ, equating the frictional energy (F × σ) to

the dissipated adhesion energy (A × ∆γ), we obtain

(9.33)

(9.34)

which is the desired expression and which has been found to give order of magnitude agreement between

measured friction forces and adhesion energy hysteresis (Chen et al., 1989). If we equate Equation 9.34

with Equation 9.32, since 4∆D/D

∆d ≈ σ, we obtain the intuitive relation:

(9.35)

Figure 9.22 illustrates the relationship between adhesion hysteresis and friction for surfactant-coated

surfaces under different conditions. This effect, however, is much more general, and has been shown to

hold for other surfaces as well (Vigil et al., 1994; Israelachvili et al., 1994, 1995). Direct comparisons

between absolute adhesion energies and friction forces show little correlation. In some cases higher

adhesion energies for the same system under different conditions correspond with lower friction forces.

For example, for hydrophilic silica surfaces it was found that with increasing relative humidity the

adhesion energy increases, but the adhesion energy hysteresis measured in a loading–unloading cycle

decreases, as does the friction force (Vigil et al., 1994). For hydrophobic silica surfaces under dry condi-

tions, the friction at load L = 5.5 mN was F = 75 mN. For the same sample, the adhesion energy hysteresis

was ∆γ = 10 mJ/m

, with a contact area of A ≈ 10

–8

at the same load. Assuming a value for the

characteristic distance σ on the order of one lattice spacing, σ ≈ 1 nm. By inserting these values into

Equation 9.33, the friction force is predicted to be F ≈ 100 mN for the kinetic friction force, which is

close to the measured value of 75 mN. Alternatively, we may conclude that the dissipation factor is ε =

0.75, i.e., that almost all the energy is dissipated as heat at each molecular collision.

9.11.4 External Load Contribution to Interfacial Friction

When there is no interfacial adhesion, S

is zero. Thus, in the absence of any adhesive forces between two

surfaces, the only “attractive” force that needs to be overcome for sliding to occur is the externally applied

load or pressure.

For a preliminary discussion of this question, it is instructive to compare the magnitudes of the

externally applied pressure to the internal van der Waals pressure between two smooth surfaces. The

internal van der Waals pressure is given by P = A/6πD

≈ 10

atm (using a typical Hamaker constant of

A = 10

–12

erg, and assuming D

≈ 2 Å for the equilibrium interatomic spacing). This implies that we

should not expect the externally applied load to affect the interfacial friction force F, as deﬁned by

Equation 9.27, until the externally applied pressure L/A begins to exceed ~1000 atm. This is in agreement

with experimental data (Briscoe et al., 1977), where the effect of load became dominant at pressures in

excess of 1000 atm.

For a more general semiquantitative analysis, again consider the cobblestone model as used to derive

Equation 9.32 but now include an additional contribution to the surface energy change of Equation 9.31

due to the work done against the external load or pressure, L∆D = P

ext

A · ∆D (this is equivalent to the

work done against gravity in the case of a cart being pushed over cobblestones). Thus,

Friction force: F

−

()

∆γ

σσ

γγ

Friction stress: SFA

==∆γσ

≈

∆

(9.36)

which gives the more general relation:

(9.37)

where P

ext

= L/A and where C

and C

are constants characteristic of the surfaces and sliding conditions.

The constant C

= (4γε · ∆D/D

· ∆d) depends on the mutual adhesion of the two surfaces, while both

and C

= ε · ∆D/∆d depend on the topography or atomic bumpiness of the surface groups

(Figure 9.21) — the smoother the surface groups the smaller the ratio ∆D/∆d and hence the lower the

value of C

. In addition, both C

and C

depend on ε — the fraction of energy dissipated per collision

which depends on the relative masses of the shearing molecules, the sliding velocity, the temperature,

and the characteristic molecular relaxation processes of the surfaces. This is by far the most difﬁcult

parameter to compute, and yet it is the most important since it represents the energy transfer mechanism

in any friction process. Further, since ε can vary between 0 and 1, it determines whether a particular

friction force will be large or close to zero. Molecular simulations offer the best way to understand and

predict the magnitude of ε, but the complex multibody nature of the problem makes simple conclusions

difﬁcult to draw. Some of the basic physics of the energy transfer and dissipation of the molecular

collisions can be drawn from simpliﬁed models (Urbakh et al., 1995; Rozman et al., 1996, 1997) such as

a one-dimensional three-body system (Israelachvili and Berman, 1995). This system, described in more

detail in Section 9.11.5, offers insight into the mechanisms of energy transfer and relates them back to

the familiar parameter De, the Deborah number.

Finally, the above equation may also be expressed in terms of the friction force F:

(9.38)

Equations similar to Equations 9.37 and 9.38 were previously derived by Derjaguin (1988, 1934) and

by Briscoe and Evans (1982), where the constant C

and C

were interpreted somewhat differently than

in this model.

In the absence of any attractive interfacial force, we have C

≈ 0, and the second term in Equations 9.37

and 9.38 should dominate. Such situations typically arise when surfaces repel each other across the

lubricating liquid ﬁlm, for example, when two mica surfaces slide across a thin ﬁlm of water (Figure 9.18).

In such cases the total frictional force should be low and it should increase linearly with the external load

according to

(9.39)

An example of such lubricated sliding occurs when two mica surfaces slide in water or in salt solution,

where the short-range hydration forces between the surfaces are repulsive. Thus, for sliding in 0.5

M KCl

it was found that C

= 0.015 (Berman et al., 1998a). Another case where repulsive surfaces eliminate the

adhesive contribution to friction is for tethered polymer chains attached to surfaces at one end and

swollen by a good solvent (Klein et al., 1994). For this class of systems C

< 0.001 for a ﬁnite range of

polymer layer compressions (normal loads, L). The low friction between the surfaces in this regime is

attributed to the entropic repulsion between the opposing brush layers with a minimum of entanglement

between the two layers. However, with higher normal loads, the brush layers become compressed and

begin to entangle, resulting in higher friction.

It is important to note that Equation 9.39 has exactly the same form as Amontons’ law:

⋅

⋅4

γε ε∆

∆

ext

SFACCP

==+

1 2 ext

FSACACL

==+

FCL=

(9.40)

where µ

is the coefﬁcient of friction. When damage occurs, there is a rapid transition to normal sliding

in the presence of wear debris. As previously described, the mechanisms of interfacial friction and normal

friction are vastly different on the submicroscopic and molecular levels. However, under certain circum-

stances both may appear to follow a similar equation (see Equations 9.39 and 9.40) even though the

friction coefﬁcients C

and µ are determined by quite different material properties in each case.

At the molecular level a thermodynamic analog of the coulomb or cobblestone models (see

Section 9.11.1) based on the contact value theorem (Israelachvili, 1991; Berman et al., 1998a; Berman

and Israelachvili, 1997) can explain why F ∝ L also holds at the microscopic or molecular level. In this

analysis we consider the surface molecular groups as being momentarily compressed and decompressed

as the surfaces move along. Under irreversible conditions, which always occur when a cycle is completed

in a ﬁnite amount of time, the energy lost in the compression/decompression cycle is dissipated as heat.

For two nonadhering surfaces, the stabilizing pressure P

acting locally between any two elemental contact

points i of the surfaces may be expressed by the contact value theorem (Israelachvili, 1992):

(9.41)

where ρ

= 1/V

is the local number density (per unit volume) or activity of the interacting entities, be

they molecules, atoms, ions, or the electron clouds of atoms. This equation is essentially the osmotic or

entropic pressure of a gas of conﬁned molecules. As one surface moves across the other, as local regions

become compressed and decompressed by a volume ∆V

, the work done per cycle can be written as ε P

∆V

, where ε (ε ≤ 1) is the fraction of energy per cycle lost as heat, as deﬁned earlier. The energy balance

shows that for each compression/decompression cycle, the dissipated energy is related to the friction

force by

(9.42)

where x

is the lateral distance moved per cycle, which can be the distance between asperities or the

distance between surface lattice sites. The pressure at each contact junction can be expressed in terms of

the local normal load L

and local area of contact A

as P

= L

. The volume change over a cycle can

thus be expressed as ∆V

= A

, where z

is the vertical distance of conﬁnement. Plugging these back into

Equation 9.42, we get

(9.43)

which is independent of the local contact area A

. The total friction force is thus

(9.44)

where it is assumed that on average, the local values of L

and P

are independent of the local “slope”

. Therefore, the friction coefﬁcient µ is a function only of the average surface topography and the

sliding velocity, but is independent of the local (real) or macroscopic (apparent) contact areas.

While this analysis explains nonadhering surfaces, there is still an additional explicit contact area

contribution for the case of adhering surfaces, as in Equation 9.38. The distinction between the two cases

arises because the initial assumption of the contact value theorem, Equation 9.41, is incomplete for

adhering systems. A more appropriate starting equation would reﬂect the full intermolecular interaction

potential, including the attractive interactions in addition to the purely repulsive contributions of

Equation 9.41, much as the van der Waals equation of state modiﬁes the ideal gas law.

FL=µ ,

PkTkTV

iiB B i

==ρ ,

Fx P V

ii i i

=ε ∆ ,

FLzx

iiii

()

ε ,

FF Lzx zxLL

i iii ii i

()

==µΣΣ Σεε ,

9.11.5 Simple Molecular Model of Energy Dissipation ε

The simple three-body system of balls and springs illustrated in Figure 9.23A provides molecular insight

into dissipative processes such as sliding friction and adhesion hysteresis. Mass m

may be considered to

constitute one body or surface that approaches another at velocity v

. Masses m

and m

represent the

other surface. As shown in Figure 9.23B, the masses of the second surface are bound together via a

parabolic (Hookian spring) potential, while masses m

and m

interact via a nonadhesive repulsion

modeled as a half parabola. Although this system is simple in appearance, it is rich in its physics. Different

relative values of the masses and spring constants lead to very different collision outcomes where the

initial translational or kinetic energy of m

is distributed among the ﬁnal kinetic, translational and

vibrational energies of m

and the m

–m

couple.

The collision is a molecular analogy, and perhaps a good microscopic representation of an adhesive

loading–unloading cycle (see Figure 9.11) or a frictional sliding process. The ﬁner molecular model of

Figure 9.23A allows us to determine exactly how the energy is being dissipated in these cycles. In a

loading–unloading process, m

represents the surface molecules of one body approaching the surface

molecules of a second body (m

and m

). Solutions to the equations of motion show that in the collision

the ﬁrst mass can be reﬂected, stopped, or even continue forward at a different velocity. In the case of

lateral sliding, the molecules of the two surfaces can still be considered to interact in this way; the surface

groups from the slider continually collide with those of the opposing surface, with the amount of the

energy transferred during the collisions deﬁning the friction. Analysis of this problem shows that the

FIGURE 9.23 (A) Schematic diagram of a basic three-body collision. Mass 1 approaches the other masses with an

initial velocity, v

. The kinetic energy of mass 1 after the collision is compared to its initial kinetic energy. The

characteristic times of the m

–m

and m

–m

interactions are functions of the respective masses and the strengths of

the connecting springs k

and k

(B). The Deborah number for this system is the ratio of the collision time between

masses 1 and 2 to the harmonic oscillating frequency of masses 2 and 3. (C) The energy transferred from mass 1 to

the rest of the system (masses 2 and 3) is plotted as a function of the Deborah number. In this calculation k

= 1,

= 10, m

= 1, and masses m

= m

were varied.

essential determinant of the amount of energy transferred from m

is based on the ratio of the collision

time to the characteristic relaxation time of the system, in other words, to the Deborah number:

(9.45)

Thus, it is found that m

loses most of its energy to the m

–m

couple when the collision time is close

to the characteristic vibration time of the m

–m

harmonic system, which corresponds to De = 1. When

the collision time is much larger or smaller than the system characteristic time, mass m

is found to

retain most of its original kinetic energy (Figure 9.23C). In this simple example, the interaction times

are functions only of the three masses, the intermolecular potential between m

and m

, and the potential

or spring constant of the m

–m

couple. In more complex systems with more realistic interaction

potentials (i.e., attractive interactions between m

and m

), the velocity v

becomes an important factor

as well, and also affects the Deborah number.

It is important to note that in this simple one-dimensional analysis, additional energy modes and

degrees of freedom of the molecules have not been considered. These modes, when present, will also be

involved in the interaction, affecting the energy transferred from m

and sharing in the ﬁnal distribution

of the energy transferred. In addition, different types of energy modes (e.g., rotational modes) will

generally have different relaxation times, so that their energy peaks will occur at different measuring

times. Such real systems may be considered to have more than one Deborah number.

The three-body system sheds some light on the molecular mechanisms of energy dissipation and the

impact of the Deborah number on the dissipation parameter ε, but because of its simplicity, does not

offer predictive capabilities for real systems. More-sophisticated models have been presented by Urbakh

et al. (1995) and Rozman et al. (1996, 1997).

9.12 Friction and Lubrication of Thin Liquid Films

When a liquid is conﬁned between two surfaces or within any narrow space whose dimensions are less

than ﬁve to ten molecular diameters, both the static (equilibrium) and dynamic properties of the liquid,

such as its compressibility and viscosity, can no longer be described even qualitatively in terms of the

bulk properties. The molecules conﬁned within such molecularly thin ﬁlms become ordered into layers

(“out-of-plane” ordering), and within each layer they can also have lateral order (“in-plane” ordering).

Such ﬁlms may be thought of as behaving more like a liquid crystal or a solid than a liquid.

As described in Section 9.4, the measured normal forces between two solid surfaces across molecularly

thin ﬁlms exhibit exponentially decaying oscillations, varying between attraction and repulsion with a

periodicity equal to some molecular dimension of the solvent molecules. Thus, most liquid ﬁlms can

sustain a ﬁnite normal stress, and the adhesion force between two surfaces across such ﬁlms is quantized,

depending on the thickness (or number of liquid layers) between the surfaces. The structuring of

molecules in thin ﬁlms and the oscillatory forces it gives rise to are now reasonably well understood,

both experimentally and theoretically, at least for simple liquids.

Work has also recently been done on the dynamic e.g., viscous or shear, forces associated with

molecularly thin ﬁlms. Both experiments (Israelachvili et al., 1988; Gee et al., 1990; Hirz et al., 1992;

Homola et al., 1993), and theory (Schoen et al., 1989; Thompson and Robbins, 1990; Thompson et al.,

1992) indicate that even when two surfaces are in steady-state sliding they still prefer to remain in one

of their stable potential energy minima, i.e., a sheared ﬁlm of liquid can retain its basic layered structure.

Thus, even during motion the ﬁlm does not become totally liquidlike. Indeed, if there is some in-plane

ordering within a ﬁlm, it will exhibit a yield point before it begins to ﬂow. Such ﬁlms can therefore sustain

a ﬁnite shear stress, in addition to a ﬁnite normal stress. The value of the yield stress depends on the

number of layers comprising the ﬁlm and represents another quantized property of molecularly thin ﬁlms.

The dynamic properties of a liquid ﬁlm undergoing shear are very complex. Depending on whether

the ﬁlm is more liquidlike or solidlike, the motion will be smooth or of the stick-slip type. During sliding,

De Relaxation time Measuring time= .

transitions can occur between n layers and (n – 1) or (n + 1) layers, and the details of the motion depend

critically on the externally applied load, the temperature, the sliding velocity, the twist angle between the

two surface lattices and the sliding direction relative to the lattices.

9.12.1 Smooth and Stick-Slip Sliding

Recent advances in friction-measuring techniques have enabled the interfacial friction of molecularly

thin ﬁlms to be measured with great accuracy. Some of these advances have involved the SFA technique

(Israelachvili et al., 1988; Gee et al., 1990; Hirz et al., 1992; Homola et al., 1989, 1990, 1993), while others

have involved the AFM (McClelland, 1989; McClelland and Cohen, 1990). In addition, molecular dynam-

ics computer simulations (Schoen et al., 1989; Landman et al., 1990; Thompson and Robbins, 1990;

Robbins and Thompson, 1991) have become sufﬁciently sophisticated to enable fairly complex tribolog-

ical systems to be studied for the ﬁrst time. All these advances are necessary if one is to probe such subtle

effects as smooth or stick-slip friction, transient and memory effects, and ultralow friction mechanisms

at the molecular level.

Figure 9.24 shows typical results for the friction traces measured as a function of time (after com-

mencement of sliding) between two molecularly smooth mica surfaces separated by three molecular

layers of the liquid OMCTS, and how the friction increases to higher values in a quantized way when

the number of layers falls from n = 3 to n = 2 and then to n = 1.

With the many added insights provided by recent computer simulations of such systems, a number

of distinct molecular processes have been identiﬁed during smooth and stick-slip sliding. These are shown

schematically in Figure 9.25 for the case of spherical liquid molecules between two solid crystalline

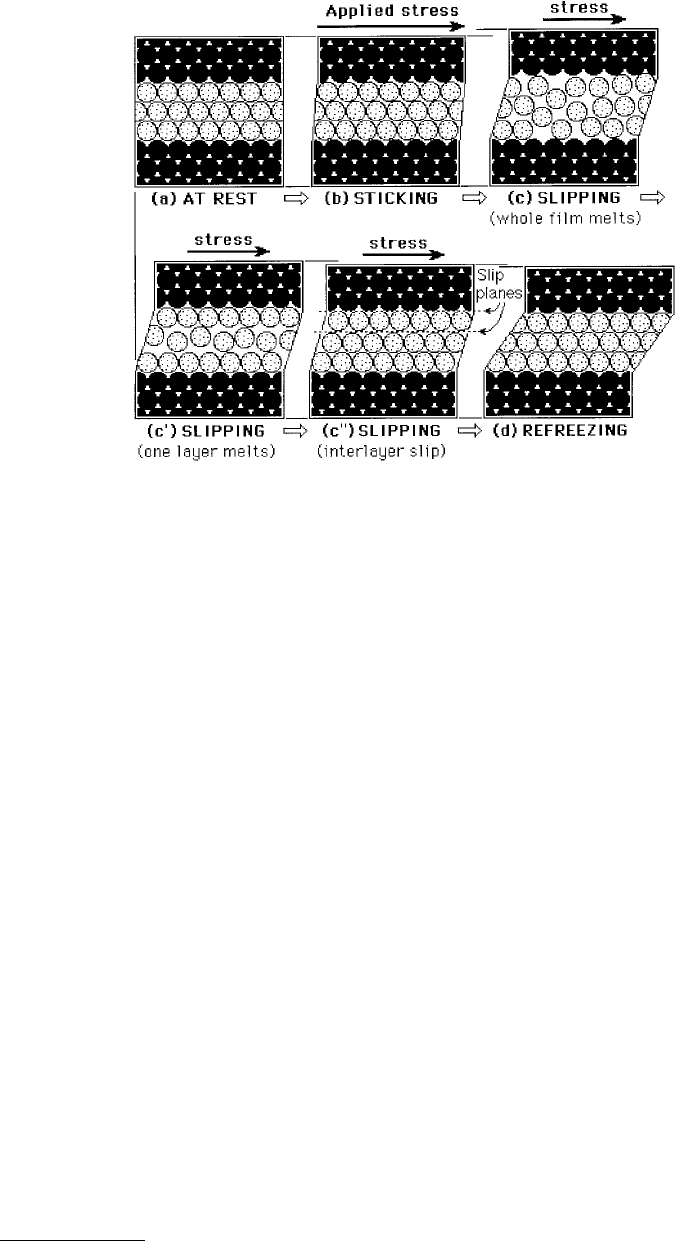
surfaces. The following regimes may be identiﬁed:

Surfaces at rest — Figure 9.25a: Even with no externally applied load, solvent–surface epitaxial inter-

actions can induce the liquid molecules in the ﬁlm to solidify. Thus at rest the surfaces are stuck to each

other through the ﬁlm.

Sticking regime (frozen, solidlike ﬁlm) — Figure 9.25b: A progressively increasing lateral shear stress is

applied. The ﬁlm, being solid, responds elastically with a small lateral displacement and a small increase

or “dilatency” in ﬁlm thickness (less than a lattice spacing or molecular dimension, σ). In this regime

the ﬁlm retains its frozen, solidlike state — all the strains are elastic and reversible, and the surfaces

remain effectively stuck to each other. However, slow creep may occur over long time periods.

FIGURE 9.24 Measured change in friction during interlayer transitions of the silicone liquid octamethylcyclotet-

rasiloxane (OMCTS, an inert liquid whose quasi-spherical molecules have a diameter of 8 Å) (Gee et al., 1990). In

this system, the shear stress S

= F/A was found to be constant so long as the number of layers n remained constant.

Qualitatively similar results have been obtained with other quasi-spherical molecules such as cyclohexane (Israelach-

vili et al., 1988). The shear stresses are only weakly dependent on the sliding velocity v. However, for sliding velocities

above some critical value v

, the stick-slip disappears and sliding proceeds smoothly in the purely kinetic value.

Slipping and sliding regimes (molten, liquidlike ﬁlm) — Figure 9.25c, c

′

, c

″

: When the applied shear

stress or force has reached a certain critical value F

, the static friction force, the ﬁlm suddenly melts

(known as shear melting) or rearranges to allow for wall slip or ﬁlm-slip to occur, at which point the

two surfaces begin to slip rapidly past each other. If the applied stress is kept at a high value, the upper

surface will continue to slide indeﬁnitely.

Refreezing regime (resolidiﬁcation of ﬁlm) — Figure 9.25d: In many practical cases, the rapid slip of the

upper surface relieves some of the applied force, which eventually falls below another critical value F

the kinetic friction force, at which point the ﬁlm resolidiﬁes and the whole stick-slip cycle is repeated.

On the other hand, if the slip rate is smaller than the rate at which the external stress is applied, the

surfaces will continue to slide smoothly in the kinetic state and there will be no more stick-slip. (Figure

9.26).The critical velocity at which stick-slip disappears is discussed in more detail in Section 9.13.

Experiments with linear-chain (alkane) molecules show that the ﬁlm thickness remains quantized

during sliding, so that the structure of such ﬁlms is probably more like that of a nematic liquid crystal

where the liquid molecules have become shear aligned in some direction enabling shear motion to occur

while retaining some order within the ﬁlm. Computer simulations for simple spherical molecules (Thomp-

son and Robbins, 1990)

further indicate that during the slip, the ﬁlm thickness is roughly 15% higher than

at rest (i.e., the ﬁlm density falls), and that the order parameter within the ﬁlm drops from 0.85 to about

0.25. Both of these are consistent with a disorganized liquidlike state for the whole ﬁlm during the slip,

as illustrated schematically in Figure 9.25c. At this stage, we can only speculate on other possible conﬁg-

urations of molecules in the slipping and sliding regimes. This probably depends on the shapes of the

molecules (e.g., whether spherical or linear or branched), on the atomic structure of the surfaces, on the

sliding velocity, etc. Figure 9.25c, c′, and c″ show three possible sliding modes wherein the shearing ﬁlm

either totally melts or where the molecules retain their layered structure and where slip occurs between

two or more layers. Other sliding modes, for example, involving the movement of dislocations or discli-

nations are also possible, and it is unlikely that one single mechanism applies in all cases.

FIGURE 9.25 Idealized schematic illustration of molecular rearrangements occurring in a molecularly thin ﬁlm of

spherical or simple chain molecules between two solid surfaces during shear. Note that, depending on the system, a

number of different molecular conﬁgurations within the ﬁlm are possible during slipping and sliding, shown here

as stages (c) — total disorder as whole ﬁlm melts, (c′) — partial disorder, and (c″) — order persists even during

sliding with slip occurring at a single slip plane either within the ﬁlm or at the walls.