Bhushan B. Handbook of Micro/Nano Tribology, Second Edition
Подождите немного. Документ загружается.

© 1999 by CRC Press LLC
because some of these are connected via spontaneous — and therefore thermodynamically irreversible —
instabilities or transitions (Figure 9.11C) where energy is liberated and therefore “lost” via heat or phonon
release (Israelachvili and Berman, 1995). This is an area of much current interest and activity, especially
regarding the fundamental molecular origins of adhesion and friction, and the relationships between them.
9.9 Rheology of Molecularly Thin Films: Nanorheology
9.9.1 Different Modes of Friction: Limits of Continuum Models
Most frictional processes occur with the sliding surfaces becoming damaged in one form or another
(Bowden and Tabor, 1967). This may be referred to as “normal” friction. In the case of brittle materials,
the damaged surfaces slide past each other while separated by relatively large, micron-sized wear particles.
With more ductile surfaces, the damage remains localized to nanometer-sized, plastically deformed
asperities.
There are also situations where sliding can occur between two perfectly smooth, undamaged surfaces.
This may be referred to as “interfacial” sliding or “boundary” friction, which is the focus of the following
sections. The term boundary lubrication is more commonly used to denote the friction of surfaces that
contain a thin protective lubricating layer, such as a surfactant monolayer, but here we shall use this term
more broadly to include any molecularly thin solid, liquid, surfactant, or polymer film.
Experiments have shown that as a liquid film becomes progressively thinner, its physical properties
change, at first quantitatively then qualitatively (Van Alsten and Granick, 1990a,b, 1991; Granick, 1991;
Hu et al., 1991; Hu and Granick, 1992; Luengo et al., 1997).
The quantitative changes are manifested by
an increased viscosity, non-Newtonian flow behavior, and the replacement of normal melting by a glass
transition, but the film remains recognizable as a liquid. In tribology, this regime is commonly known
as the “mixed lubrication” regime, where the rheological properties of a film are intermediate between
the bulk and boundary properties. One may also refer to it as the “intermediate” regime (Table 9.3).
For even thinner films, the changes in behavior are more dramatic, resulting in a qualitative change
in properties. Thus, first-order phase transitions can now occur to solid or liquid-crystalline phases (Gee
et al., 1990; Israelachvili et al., 1990a,b; Thompson and Robbins, 1990; Yoshizawa et al., 1993; Klein and
Kumacheva, 1995), whose properties can no longer be characterized — even qualitatively — in terms of
bulk or continuum liquid properties such as viscosity. These films now exhibit yield points (characteristic
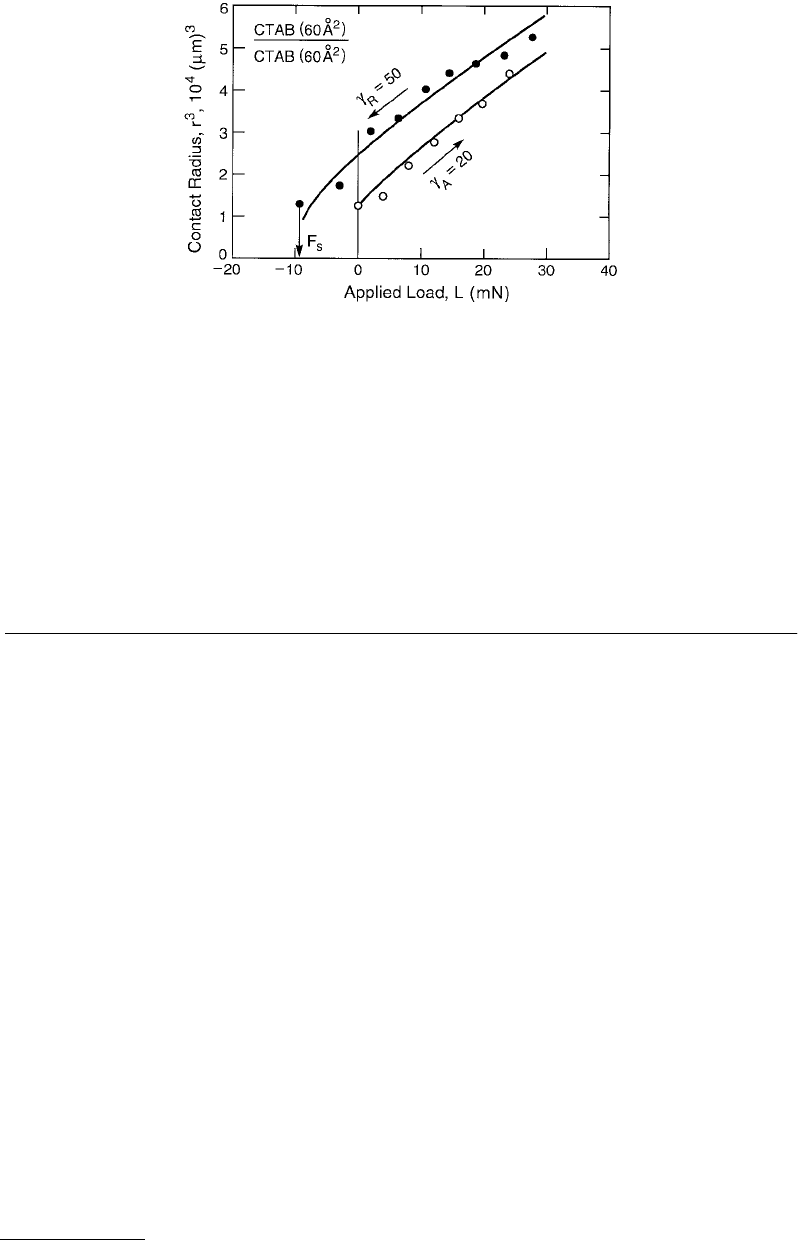
FIGURE 9.12 Measured advancing and receding radius vs. load curves for two surfactant-coated mica surfaces of
initial, undeformed radii R ≈ 1 cm. Each surface had a monolayer of CTAB (cetyl-trimethyl-ammonium-bromide)
on it of mean area 60 Å
2
per molecule. The solid lines are based on fitting the advancing and receding branches to
the JKR equation, Equation 9.20), from which the indicated values of γ
A
and γ
R
were determined, in units of mJ/m
2
or erg/cm
2
. The advancing/receding rates were about 1 µm/s. At the end of each unloading cycle the pull-off force,
F
s
, can be measured, from which another value for γ
R
can be obtained using Equation 9.21).

© 1999 by CRC Press LLC
of fracture in solids) and their molecular diffusion and relaxation times can be ten orders of magnitude
longer than in the bulk liquid or even in films that are just slightly thicker. The three friction regimes
are summarized in Table 9.3.
9.9.2 Viscous Forces and Friction of Thick Films: Continuum Regime
Experimentally, it is usually difficult to unambiguously establish which type of sliding mode is occurring,
but an empirical criterion, based on the Stribeck curve (Figure 9.13) is often used as an indicator. This
curve shows how the friction force or the coefficient of friction is expected to vary with sliding speed
depending on which type of friction regime is operating. For thick liquid lubricant films whose behavior
can be described by bulk continuum properties, the friction forces are essentially the hydrodynamic or
viscous drag forces. For example, for two plane parallel surfaces of area A separated by a distance D and
moving laterally relative to each other with velocity v, if the intervening liquid is Newtonian, i.e., if its
viscosity η is independent of the shear rate, the frictional force experienced by the surfaces is given by
(9.24)
where the shear rate
·
γ is defined by
(9.25)
TABLE 9.3 The Three Main Tribological Regimes Characterizing the Changing Properties of Liquids Subjected
to an Increasing Confinement between Two Solid Surfaces
a
Regime
Conditions for Getting into
this Regime
Static/Equilibrium
Properties
b
Dynamic Properties
c
Bulk • Thick films (>10σ, »R
g
)
• Low or zero loads
• High shear rates
Bulk, continuum properties:
• Bulk liquid density
• No long-range order
Bulk, continuum properties:
• Newtonian viscosity
• Fast relaxation times
• No glass temperature
• No yield point
• EHD lubrication
Mixed or
intermediate
• Intermediately thick films
(4–10 molecular
diameters ~R
g
for
polymers)
• Low loads
Modified fluid properties include:
• Modified positional and
orientational order
a
• Medium to long-range molecular
correlations
• Highly entangled states
Modified rheological properties
include:
• Non-Newtonian flow
• Glassy states
• Long relaxation times
• Mixed lubrication
Boundary • Molecularly thin films (<4
molecular diameters)
• High loads
• Low shear rates
• Smooth surfaces or
asperities
Onset of non-fluidlike properties:
• Liquidlike to solidlike phase
transitions
• Appearance of new liquid-crystalline
states
• Epitaxially induced long-range
ordering
Onset of tribological properties:
• No flow until yield point or critical
shear stress reached
• Solidlike film behavior
characterized by defect diffusion,
dislocation motion, shear melting
• Boundary lubrication
Based on work by Granick (1991), Hu and Granick (1992), and others (Gee et al., 1990; Hirz et al., 1992; Yoshizawa et al.,
1993) on the dynamic properties of short-chain molecules such as alkanes and polymer melts confined between surfaces.
a
Confinement can lead to an increased or decreased order in a film, depending both on the surface lattice structure and the
geometry of the confining cavity.
b
In each regime both the static and dynamic properties change. The static properties include the film density, the density
distribution function, the potential of mean force, and various positional and orientational order parameters.
c
Dynamic properties include viscosity, viscoelastic constants, and tribological yield points such as the friction coefficient and
critical shear stress.
F
Av
D
=
η
,
˙
.γ=
V
D
© 1999 by CRC Press LLC
At higher shear rates, two additional effects often come into play. First, certain properties of liquids
may change at high
·
γ values. In particular, the “effective” viscosity may become non-Newtonian, one
form given by
(9.26)
where n = 0 for Newtonian fluids, n > 0 for shear thickening (dilatent) fluids, and n < 0 for shear thinning
(pseudoplastic) fluids (the latter become less viscous, i.e., flow more easily, with increasing shear rate).
An additional effect on η can arise from the higher local stresses (pressures) experienced by the liquid
film
as
·
γ increases. Since the viscosity is generally also sensitive to the pressure (usually increasing with
P), this effect also acts to increase η
eff
and thus the friction force.
A second effect that occurs at high shear rates is surface deformation, arising from the large hydro-
dynamic forces acting on the sliding surfaces. For example, Figure 9.13B shows how two surfaces elastically
deform when the sliding speed increases to a high value. These deformations alter the hydrodynamic
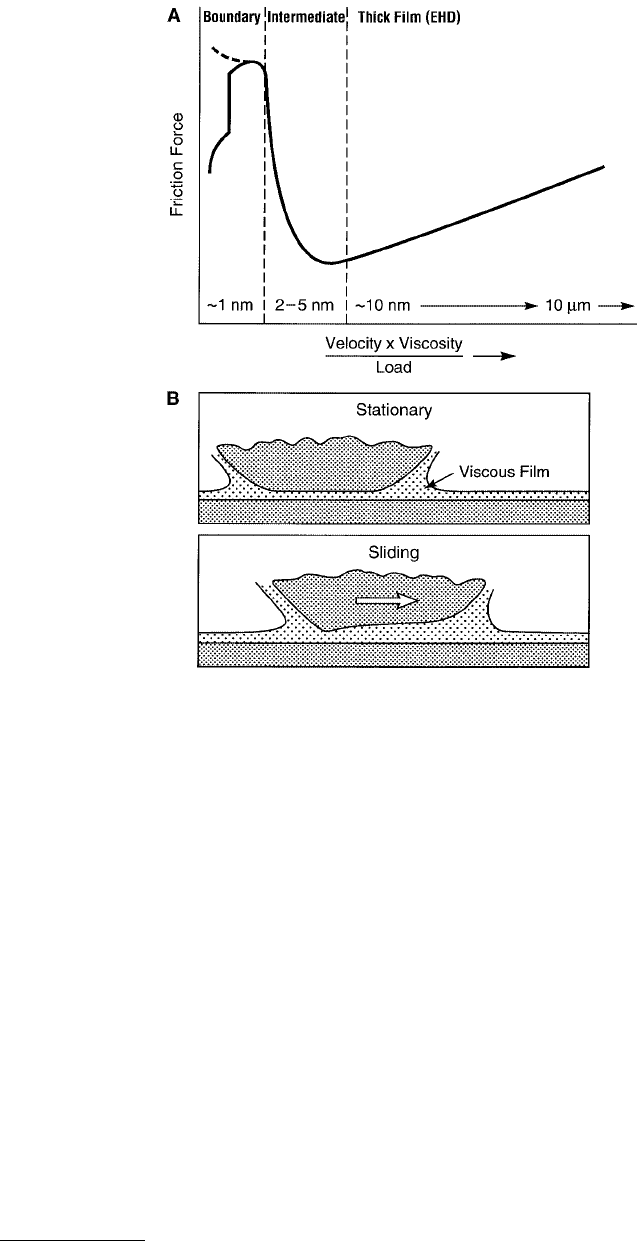
FIGURE 9.13 (A) Stribeck curve: empirical curve giving the trend generally observed in the friction forces or
friction coefficients as a function of sliding velocity, the bulk viscosity of the lubricating fluid, and the applied load.
The three friction/lubrication regimes are known as the thick-film or EHD lubrication regime (see B below), the
intermediate or mixed lubrication regime (see Figure 9.14), and the boundary lubrication regime (see Figure 9.24).
The film thicknesses, believed to correspond to each of these regimes, are also shown. For thick films the friction
force is purely viscous e.g., Couette flow at low shear rates, but may become complicated at higher shear rates where
EHD deformations of surfaces can occur during sliding, as shown in (B).
ηγ
eff
=
˙
n
© 1999 by CRC Press LLC
friction forces, and this type of friction is often referred to as elastohydrodynamic lubrication (EHD or
EHL) as mentioned in Table 9.3.
One natural question is: How thin can a liquid film be before its dynamic e.g., viscous flow, behavior
ceases to be described by bulk properties and continuum models? Concerning the static properties, we
have already seen that films composed of simple liquids display continuum behavior down to thicknesses
of 5 to 10 molecular diameters. Similar effects have been found to apply to the dynamic properties, such
as the viscosity, of simple liquids in thin films. Concerning viscosity measurements, a number of dynamic
techniques were recently developed (Chan and Horn, 1985; Israelachvili, 1986a; Van Alsten and Granick,
1988; Israelachvili and Kott, 1989) for directly measuring the viscosity as a function of film thickness
and shear rate across very thin liquid films between two surfaces. By comparing the results with theoretical
predictions of fluid flow in thin films, one can determine the effective positions of the shear planes and
the onset of non-Newtonian behavior in very thin films.
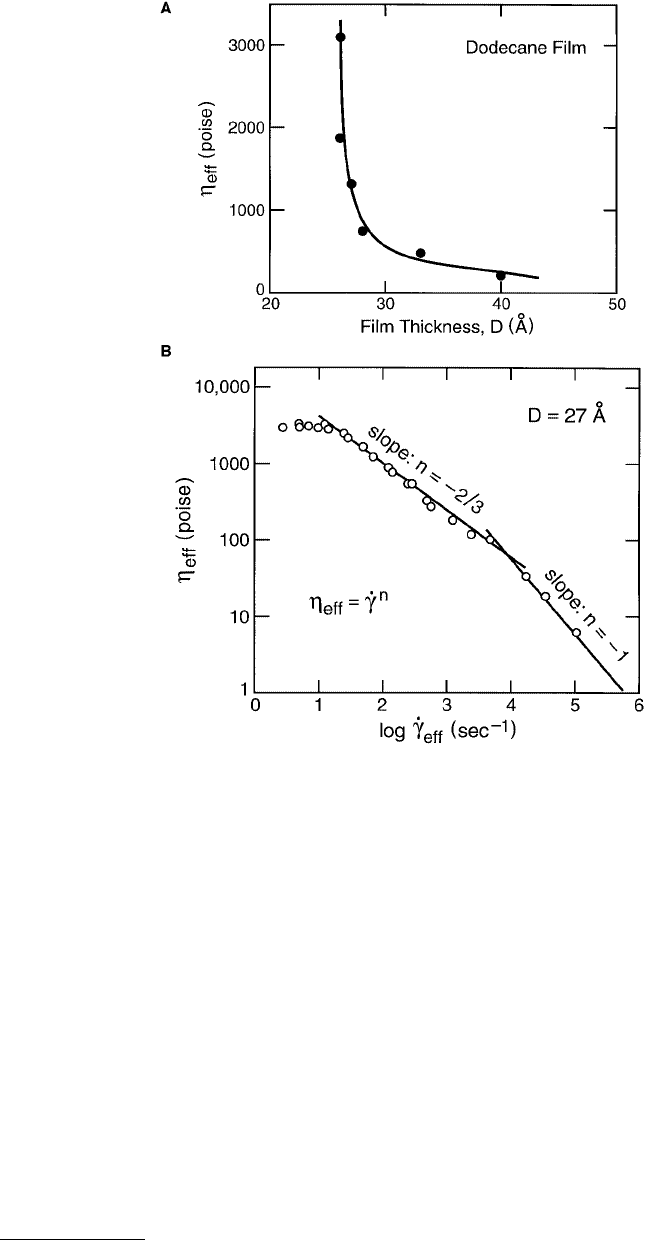
FIGURE 9.14 Typical rheological behavior of liquid film in the mixed lubrication regime. (A) Increase in effective
viscosity of dodecane film between two mica surfaces with decreasing film thickness (Granick, 1991). Beyond 40 to
50 Å, the effective viscosity η
eff
approaches the bulk value η
bulk
. (B) Non-Newtonian variation of η
eff
with shear rate
of a 27-Å-thick dodecane film (from Luengo et al., 1996). The effective viscosity decays as a power law, as in
Equation 9.26. In this example, n = 0 at the lowest
·
γ
, then transitions to n = –1 at higher
·
γ
. For bulk thick films,
dodecane is a low-viscosity Newtonian fluid (n = 0).

© 1999 by CRC Press LLC
The results show that for simple liquids including linear-chain molecules such as alkanes, their viscosity
in thin films is the same, within 10%, as the bulk even for films as thin as ten molecular diameters (or
segment widths) (Chan and Horn, 1985; Israelachvili, 1986a; Israelachvili and Kott, 1989). This implies
that the shear plane is effectively located within one molecular diameter of the solid liquid interface, and
these conclusions were found to remain valid even at the highest shear rates studied (of ~2 × 10
5
s
–1
).
With water between two mica or silica surfaces (Chan and Horn, 1985; Israelachvili, 1986a; Horn et al.,
1989b; Israelachvili and Kott, 1989), this has been found to be the case (to within ±10%) down to surface
separations as small as 2 nm, implying that the shear planes must also be within a few angstrom of the
solid–liquid interfaces. These results appear to be independent of the existence of electrostatic double-
layer or hydration forces. For the case of the simple liquid toluene confined between surfaces with
adsorbed layers of C
60
molecules, this type of viscosity measurement has shown that the traditional no-
slip assumption for flow at a solid interface does not always hold (Campbell et al., 1996). For this system,
the C
60
layer at the mica–toluene interface results in a “full-slip” boundary, which dramatically lowers
the viscous drag or effective viscosity for regular Couette or Poiseuille flow.
With polymeric liquids (polymer melts) such as polydimethylsiloxanes (PDMS) and polybutadienes
(PBD), or polystyrene (PS) adsorbed onto surfaces from solution, the far-field viscosity is again equal
to the bulk value, but with the no-slip plane (hydrodynamic layer thickness) being located at D = 1 to
2 R
g
away from each surface (Israelachvili, 1986b; Luengo et al., 1997), or at D = L for polymer brush
layers of thickness L per surface (Klein et al., 1993). In contrast, the same technique was used to show
that for nonadsorbing polymers in solution, there is actually a depletion layer of nearly pure solvent that
exists at the surfaces that affects the confined solution flow properties (Kuhl et al., 1998). These effects
are observed from near contact to surface separations in excess of 200 nm.
Further experiments with surfaces closer than a few molecular diameters (D < 20 to 40 Å for simple
liquids, or D < 2 to 4 R
g
for polymer fluids) indicate that large deviations occur for thinner films, described
below. One important conclusion from these studies is therefore that the dynamic properties of simple
liquids, including water, near an isolated surface are similar to those of the bulk liquid already within the
first layer of molecules adjacent to the surface, only changing when another surface approaches the first.
In other words, the viscosity and position of the shear plane near a surface are not simply a property of
that surface, but of how far that surface is from another surface. The reason for this is because when two
surfaces are close together, the constraining effects on the liquid molecules between them are much more
severe than when there is only one surface. Another obvious consequence of the above is that one should
not make measurements on a single, isolated solid–liquid interface and then draw conclusions about the
state of the liquid or its interactions in a thin film between two surfaces.
9.9.3 Friction of Intermediate Thickness Films
For liquid films in the thickness range between 6 and 10 molecular diameters, their properties can be
significantly different from those of bulk films. But the fluids remain recognizable as fluids; in other
words, they do not undergo a phase transition into a solid or liquid-crystalline phase. This regime has
recently been studied by Granick and co-workers (Van Alsten and Granick, 1990a,b, 1991; Granick, 1991;
Hu et al., 1991; Hu and Granick, 1992; Klein and Kumacheva, 1995) who used a different type of friction
attachment (Van Alsten and Granick, 1988, 1990b) to the SFA where the two surfaces are made to vibrate
laterally past each other at small amplitudes. This method provides information on the real and imaginery
parts (elastic and dissipative components, respectively) of the shear modulus of thin films at different
shear rates and film thickness. Granick (1991) and Hu et al. (1991) found that films of simple liquids
become non-Newtonian in the 25 to 50 Å regime (about ten molecular diameters), whereas polymer
melts become non-Newtonian at much thicker films, depending on their molecular weight (Luengo et al.,
1997).
A generalized friction map (Figure 9.16) has been proposed by Luengo et al. (1996) that illustrates the
changes in η
eff
from bulk Newtonian behavior (n = 0, η
eff
= η
bulk
) through the transition regime where
© 1999 by CRC Press LLC
n reaches a minimum of –1 with decreasing shear rate, to the solidlike creep regime at very low
·
γ, where
n returns to 0. The data in Figure 9.15 show the transition for thicker polymer films from bulk behavior
to the tribological regime where n reaches –1 (Luengo et al., 1997). With further decreasing shear rates
the exponent n increases from –1 to 0, as illustrated in Figure 9.14B for a dodecane system. A number
of results from experimental, theoretical, and computer simulation work have shown values of n from
–½ to –1 for this transition regime for a variety of systems and assumptions (Hu and Granick, 1992;
Granick, 1991; Thompson et al., 1992, 1995; Urbakh et al., 1995; Rabin and Hersht, 1993).
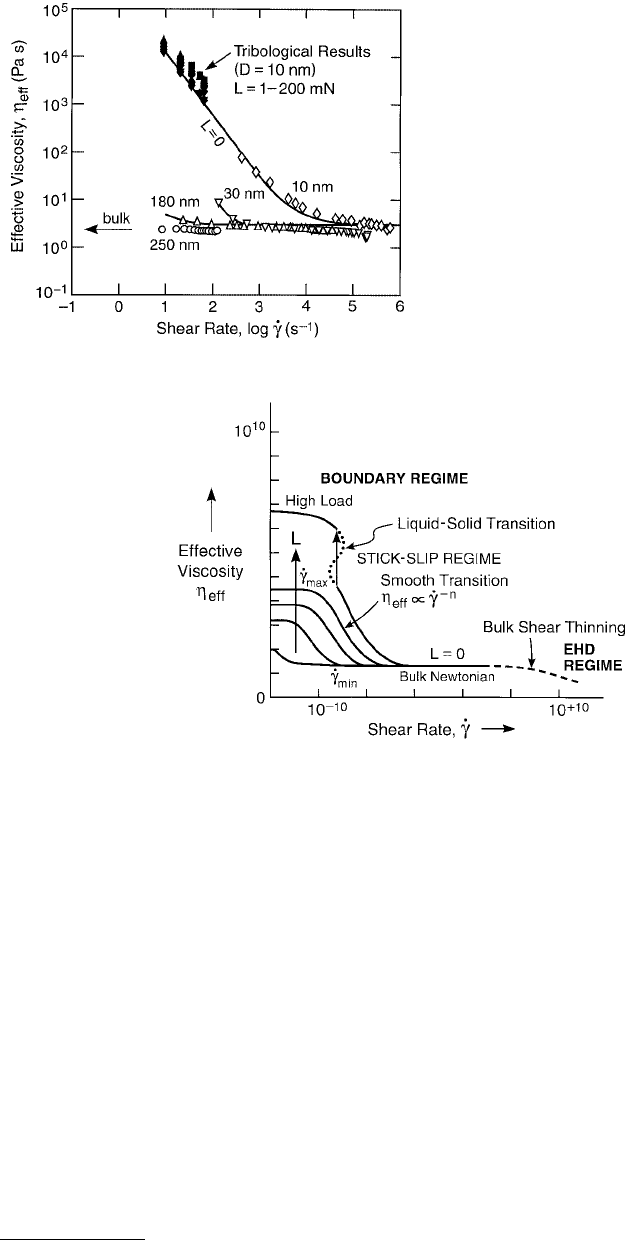
FIGURE 9.15 Effective viscosity plotted against
effective shear rate on log–log scales for polybutadi-
ene (MW = 7000) at four different separations, D
(adapted from Luengo et al., 1997). Open data
points were obtained from sinusoidally applied shear
at zero load (L = 0) at the indicated separations.
Solid points were obtained from friction experi-
ments at constant-sliding velocities. These tribolog-
ical results extrapolate, at high shear rate, to the bulk
viscosity.
FIGURE 9.16 Proposed generalized friction map of effective viscosity plotted against effective shear rate on a log–log
scale. (From Luengo, G. et al., 1996, Wear 200, 328–335. With permission.) Three main classes of behavior emerge:
(1) Thick films; EHD sliding. At zero load (L = 0), approximating bulk conditions, η
eff
is independent of shear rate
except when shear thinning may occur at sufficiently large
·
γ
. (2) Boundary layer films, intermediate regime. A
Newtonian regime is again observed (η
eff
= constant, n = 0 in Equation 9.26) at low loads and low shear rates, but
η
eff
is much higher than the bulk value. As the shear rate
·
γ
increases beyond
·
γ
min
, the effective viscosity starts to drop
with a power law dependence on the shear rate (see Figure 9.14B), with n in the range of – ½ to –1 most commonly
observed. As the shear rate
·
γ
increases still more, beyond
·
γ
max
, a second Newtonian plateau is again encountered.
(3) Boundary layer films, high load. The η
eff
continues to grow with load and to be Newtonian provided that the
shear rate is sufficiently low. Transition to sliding at high velocity is discontinuous (n < –1) and usually of the stick-
slip variety.

© 1999 by CRC Press LLC
The intermediate regime appears to extend over a narrow range of film thickness, from about four to
ten molecular diameters or polymer radii of gyration. Thinner films begin to adopt “boundary” or
“interfacial” friction properties (described below, see also Table 9.3). Note that the intermediate regime
is actually a very narrow one when defined in terms of film thickness, for example, varying from about
D = 20 to 40 Å for hexadecane films (Granick, 1991).
The effective viscosity η
eff
of a fluid in the intermediate regime is usually higher than in the bulk, but
η
eff
usually decreases with increasing sliding velocity, v (known as shear thinning). When two surfaces
slide in the intermediate regime, the motion tends to thicken the film (dilatency). This sends the system
into the bulk EHL regime where, as indicated by Equation 9.24, the friction force now increases with velocity.
This initial decrease, followed by an increase, in the frictional forces of many lubricant systems is the basis
for the empirical Stribeck curve of Figure 9.13A. In the transition from bulk to boundary behavior there is
first a quantitative change in the material properties (viscosity and elasticity) which can be continuous, to
discontinuous qualitative changes which result in yield stresses and non-liquidlike behavior.
The rest of this chapter is devoted to friction in the interfacial and boundary regimes. The former
(interfacial friction) may be thought of as applying to the sliding of two dry, unlubricated surfaces in
true molecular contact. The latter (boundary friction) may be thought of as applying to the case where
a lubricant film is present, but where this film is of molecular dimensions — a few molecular layers or less.
9.10 Interfacial and Boundary Friction: Molecular Tribology
9.10.1 General Interfacial Friction
When a lateral force, or shear stress, is applied to two surfaces in adhesive contact, the surfaces initially
remain “pinned” to each other until some critical shear force is reached. At this point, the surfaces begin
to slide past each other either smoothly or in jerks. The frictional force needed to initiate sliding from
rest is known as the static friction force, denoted by F
s
, while the force needed to maintain smooth sliding
is referred to as the kinetic or dynamic friction force, denoted by F
k
. In general, F
s
> F
k
. Two sliding
surfaces may also move in regular jerks, known as “stick-slip” sliding, which is discussed in more detail
in Section 9.13. Note that such friction forces cannot be described by equations, such as Equation 9.26,
used for thick films that are viscous and therefore shear as soon as the smallest shear force is applied.
Experimentally, it has been found that during both smooth and stick-slip sliding the local geometry
of the contact zone remains largely unchanged from the static geometry, and that the contact area vs.
load is still well described by the JKR equation, Equation 9.20.
The friction force of two molecularly smooth surfaces sliding while in adhesive contact with each other
is not simply proportional to the applied load, L, as might be expected from Amontons’ law. There is an
additional adhesion contribution that is proportional to the area of contact, A, which is described later.
Thus, in general, the interfacial friction force of dry, unlubricated surfaces sliding smoothly past each
other is given by
(9.27)
where S
c
is the critical shear stress (assumed to be constant), A = πr
2
is the contact area of radius r given
by Equation 9.20, and µ is the coefficient of friction. For low loads we have
(9.28)
while for high loads, Equation 9.27 reduces to Amontons’ law:
(9.29)
FF SA L
kc
== +µ.
FSASr S
R
K
LR RL R
cc c
==π=π +π+π+π
()
2
2
23
6126γγγ,
FL=µ .

© 1999 by CRC Press LLC
Depending on whether the friction force, F, in Equation 9.27 is dominated by the first or second terms,
one may refer to the friction as adhesion controlled or load controlled, respectively.
Figure 9.17 shows a plot of contact area, A, and friction force, F, both plotted against the applied load,
L, in an experiment where two molecularly smooth surfaces of mica in adhesive contact were slid past
each other in an atmosphere of dry nitrogen gas. This is an example of the low-load, adhesion-controlled
limit, which is excellently described by Equation 9.28. In a number of different experiments, S
c
was
measured to be
2.5 × 10
7
N/m
2
, and to be independent of the sliding velocity. Note that there is a friction
force even at negative loads, where the surfaces are still sliding in adhesive contact.
9.10.2 Boundary Friction of Surfactant Monolayer–Coated Surfaces
The high friction force of unlubricated sliding can often be reduced by treating the solid surface with a
boundary layer of some other solid material that exhibits lower friction, such as a surfactant monolayer,
or by ensuring that during sliding, a thin liquid film remains between the surfaces. The effectiveness of
a solid boundary lubricant layer on reducing the forces of friction is illustrated in Figure 9.18. Comparing
this with the friction of the unlubricated/untreated surfaces (Figure 9.17) shows that the critical shear
stress has been reduced by a factor of about 10: from 2.5 × 10
7
to 3.5 × 10
6
N/m
2
. At much higher applied
loads or pressures, the friction force is proportional to the load rather than the area of contact (Briscoe
et al., 1977), as expected from Equation 9.27.
9.10.3 Boundary Lubrication of Molecularly Thin Liquid Films
A liquid lubricant film is usually much more effective at lowering the friction of two surfaces than a solid
boundary lubricant layer. However, to use a liquid lubricant successfully, it must “wet” the surfaces; that
is, it should have a high affinity for the surfaces so that the liquid molecules do not become squeezed
out when the surfaces come close together, even under a large compressive load. Another important
requirement is that the liquid film remains a liquid under tribological conditions, i.e., that it does not
epitaxially solidify between the surfaces.
Effective lubrication usually requires that the lubricant be injected between the surfaces, but in some
cases the liquid can be made to condense from the vapor. Both of these effects are illustrated in Figure 9.19
for two untreated mica surfaces sliding with a thin layer of water between them. We may note that a
monomolecular film of water (of thickness 2.5 Å per surface) has reduced S
c
by a factor of more than 30,
FIGURE 9.17 Friction force F and contact area A vs. load L for two mica surfaces sliding in adhesive contact in
dry air. The contact area is well described by the JKR theory, Equation 9.20), even during sliding, and the frictional
force is found to be directly proportional to this area, Equation 9.28. The vertical dashed line and arrow show the
transition from interfacial to normal friction with the onset of wear (lower curve).
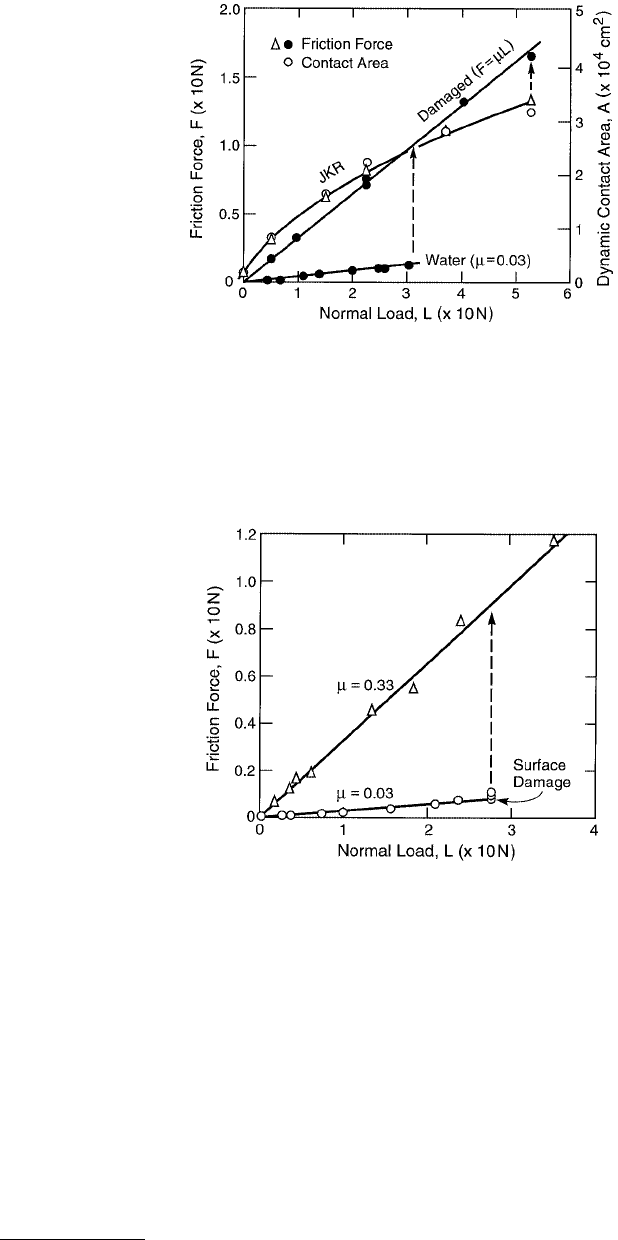
© 1999 by CRC Press LLC
which may be compared with the factor of 10 attained with the boundary lubricant layer (of thickness
25 Å per surface).
The effectiveness of a water film only 2.5 Å thick to lower the friction force by more than an order of
magnitude is attributed to the “hydrophilicity” of the mica surface (mica is “wetted” by water) and to
the existence of a strongly repulsive short-range hydration force between such surfaces in aqueous
solutions (see Section 9.6) which effectively removes the adhesion-controlled contribution to the friction
force (Berman et al., 1998a). It is also interesting that a 2.5-Å-thick water film between two mica surfaces
is sufficient to bring the coefficient of friction down to 0.01 to 0.02, a value that corresponds to the
unusually low friction of ice. Clearly, a single monolayer of water can be a very good lubricant — much
better than most other monomolecular liquid films, for reasons that will be discussed below.
FIGURE 9.18 Sliding of mica surfaces each coated with a 25-Å-thick monolayer of calcium stearate surfactant in
the absence of damage (obeying JKR-type boundary friction) and in the presence of damage (obeying Amontons-
type normal friction). (Homola et al., 1989, 1990).
At much higher applied loads the undamaged surfaces also follow
Amontons-type sliding,
but for different reasons (see next section). Lower line: interfacial sliding with a monolayer
of water between the mica surfaces, shown for comparison. Note that in both cases, after damage occurs, the friction
force obeys Amontons’ law with the same coefficient of friction of µ ≈ 0.3.
FIGURE 9.19 Two mica surfaces sliding past each other while immersed in a 0.01
M KCl salt solution. In both cases
the water film is molecularly thin: 2.5 to 5.0 Å thick, and the interfacial friction force is very low: S
c
≈ 5 × 10
5
N/m
2
,
µ ≈ 0.015 (before damage occurs).

© 1999 by CRC Press LLC
9.10.4 Transition from Interfacial to Normal Friction (with Wear)
Frictional damage can have many causes such as adhesive tearing at high loads or overheating at high
sliding speeds. Once damage occurs, there is a transition from “interfacial” to “normal” or load-controlled
friction as the surfaces become forced apart by the torn-out asperities (wear particles). For low loads,
the friction changes from obeying F = S
c
A to obeying Amontons’ law: F = µL, as shown in Figures 9.17
through 9.20, and sliding now proceeds smoothly with the surfaces separated by a 100 to 1,000 Å forest
of wear debris (mica or alumina flakes in this case). The wear particles keep the surfaces apart over an
area that is much greater than their size, so that even one submicroscopic particle or asperity can cause
a significant reduction in the area of contact and therefore in the friction (Homola et al., 1990). For this
type of frictional sliding, one can no longer talk of the molecular contact area of the two surfaces, although
the macroscopic or “apparent” area is still a useful parameter. A further discussion on the impact of
normal load and contact area is found in Section 9.11.4.
One remarkable feature of the transition from interfacial to normal friction of brittle surfaces is that
while the strength of interfacial friction, as reflected in the values of S
c
, is very dependent on the type of
surface and on the liquid film between the surfaces, this is not the case once the transition to normal
friction has occurred. At the onset of damage, it is the material properties of the underlying substrates
that control the friction. In Figures 9.17 through 9.19 the friction for the damaged surfaces is that of any
damaged mica–mica system, while in Figure 9.20 the damaged surfaces friction is that of general alu-
mina–alumina sliding (with a friction coefficient that agrees with literature values for the bulk materials),
independent of the initial surface coatings or liquid films between the surfaces.
In order to modify practically the frictional behavior of such brittle materials, it is important to use
coatings that will both alter the interfacial tribological character and remain intact and protect the surfaces
from damage during sliding (Berman et al., 1998b). An example of the friction behavior of a strongly
FIGURE 9.20 Friction forces as a function of load for smooth (undamaged) and rough (damaged) surfaces (Berman
et al., 1998b). Untreated alumina surfaces (curve a) exhibit the lowest friction due to a thin physisorbed layer of
lubricating contaminants, but these are easily damaged upon sliding, resulting in rough surface (curve b) with a
higher friction. Monolayer coated surfaces (curve c) slide with higher friction at lower loads than untreated alumina,
but remain undamaged even after prolonged sliding, keeping the friction and wear substantially lower than rough
surfaces at high loads. Smooth sliding was “adhesion controlled,” i.e., the contact area A is well described by the JKR
equation (Equation 9.20), and F/A = constant (Equation 9.28). In addition, F is finite at L = 0. Rough, damaged
sliding was “load controlled”; i.e., the real contact area is undefined, and F ∝ L (Equation 9.29) with F ≈ 0 at L = 0.
Experimental conditions: sliding velocity V = 0.05 to 0.5 µm/s; undeformed radius of curved surfaces, R ≈ 1 cm;
temperature T = 25°C; contact pressure range, P = 0 to 10 MPa; relative humidity, RH = 0% (curves a and c), RH =
0% and 100% (curve b).
