Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

9.12.2 Role of Molecular Shape and Liquid Structure

The above scenario is already quite complicated, and yet this is the situation for the simplest type of

experimental system. The factors that appear to determine the critical velocity v

depend on the type of

liquid between the surfaces (as well as on the surface lattice structure). Small spherical molecules such

as cyclohexane and OMCTS have been found to have very high v

, which indicates that these molecules

can rearrange relatively quickly in thin ﬁlms. Chain molecules and especially branched chain molecules

have been found to have much lower v

, which is to be expected, and such liquids tend to slide smoothly

rather than in a stick-slip fashion (see Table 9.4). With highly asymmetric molecules, such as multiply

branched isoparafﬁns and polymer melts, no regular spikes or stick-slip behavior occurs at any speed

since these molecules can never order themselves sufﬁciently to “solidify.” Examples of such liquids are

perﬂuoropolyethers and polydimethylsiloxanes (PDMS).

Table 9.4 shows the trends observed with some organic and polymeric liquid between smooth mica

surfaces. Also listed are the bulk viscosities of the liquids. From the data of Table 9.4 it appears that there

is a direct correlation between the shapes of molecules and their coefﬁcient of friction or effectiveness

as lubricants (at least at low shear rates). Small spherical or chain molecules have high friction with stick-

slip because they can pack into ordered solidlike layers. In contrast, longer-chained and irregularly shaped

FIGURE 9.26 Stiction is the high starting frictional force F

experienced by two moving surfaces which causes them

to jerk forward rather than accelerate smoothly from rest. It is a major cause of surface damage and wear. The ﬁgure

shows a typical “stiction spike” or “starting spike,” followed by smooth sliding in the kinetic state.

TABLE 9.4 Effect of Molecular Shape and Short-Range Forces on Tribological Properties

Short-Range Type of Friction Bulk Liquid

Liquid (Dry) Force Friction Coefﬁcient Viscosity (cP)

Organic

Cyclohexane Oscillatory Quantized stick-slip »1 0.6

Octane Oscillatory Quantized stick-slip 1.5 0.5

Tetradecane Oscil↔smooth Stick-slip↔smooth 1.0 2.3

Octadecane (branched) Oscil↔smooth Stick-slip↔smooth 0.3 5.5

PDMS (M = 3700, melt) Oscil↔smooth Smooth 0.4 50

PBD (M = 3500, branched) Smooth Smooth 0.03 800.0

Wat er

Water (KCl solution) Smooth Smooth 0.01–0.03 1.0

For molecularly thin liquid ﬁlms between two shearing mica surfaces at 20°C.

Note:

PDMS: Polydimethylsiloxane, PBD: Polybutadiene.

molecules remain in an entangled, disordered, ﬂuidlike state even in very thin ﬁlms and these give low

friction and smoother sliding. It is probably for this reason that irregularly shaped branched chain

molecules are usually better lubricants. It is interesting to note that the friction coefﬁcient generally

decreases as the bulk viscosity of the liquids increases. This unexpected trends occurs because the factors

that are conducive to low friction are generally conducive to high viscosity. Thus, molecules with side

groups such as branched alkanes and polymer melts usually have higher bulk viscosities than their linear

homologues for obvious reasons. However, in thin ﬁlms the linear molecules have higher shear stresses

because of their ability to become ordered. The only exception to the above correlations is water, which

has been found to exhibit both low viscosity and low friction (see Figure 9.19). In addition, the presence

of water can drastically lower the friction and eliminate the stick-slip of hydrocarbon liquids when the

sliding surfaces are hydrophilic.

If an effective viscosity η

eff

were to be calculated for the liquids of Table 9.1, the values would be many

orders of magnitude higher than those of the bulk liquids. This can be demonstrated by the following

simple calculation based on the usual equation for Couette ﬂow (see Equation 9.24):

(9.46)

where F

is the kinetic friction force, D is the ﬁlm thickness, A the contact area, and v the sliding velocity.

By using typical values for experiments with hexadecane (Yoshizawa and Israelachvili, 1993) — F

5 mN, D = 1 nm, A = 3 × 10

–9

and v = 1 µm/s — yields η

eff

≈ 2000 N m

–2

s, or 20,000 P, which is

~10

times higher than the bulk viscosity η

bulk

of the liquid. It is instructive to consider that this very

high effective viscosity nevertheless still produces a low friction force or friction coefﬁcient µ of about

0.25. It is interesting to speculate that if a 1-nm ﬁlm were to exhibit bulk viscous behavior, the friction

coefﬁcient under the same sliding conditions would be as low as 0.000001. While such a low value has

never been reported for any tribological system, one may consider it as a theoretical lower limit that

could, conceivably, be attained under certain experimental conditions.

Various studies (Van Alsten and Granick, 1990a,b, 1991; Granick, 1991; Hu and Granick, 1992) have

shown that conﬁnement and load generally increase the effective viscosity and/or relaxation times of

molecules, suggestive of an increased glassiness or solidlike behavior. This is in marked contrast to studies

of liquids in small conﬁning capillaries where the opposite effects have been observed (Warnock et al.,

1986; Awschalom and Warnock, 1987). The reason for this is probably because the two modes of

conﬁnement are different. In the former case (conﬁnement of molecules between two structured solid

surfaces) there is generally little opposition to any lateral or vertical displacement of the two surface

lattices relative to each other. This means that the two lattices can shift in the x-y-z plane (Figure 9.27A)

to accommodate the trapped molecules in the most crystallographically commensurate or “epitaxial”

way, which would favor an ordered, solidlike state. In contrast, the walls of capillaries are rigid and cannot

easily move or adjust to accommodate the conﬁned molecules (Figure 9.27B), which will therefore be

forced into a more disordered, liquidlike state (unless the capillary wall geometry and lattice is exactly

commensurate with the liquid molecules, as occurs in certain zeolites).

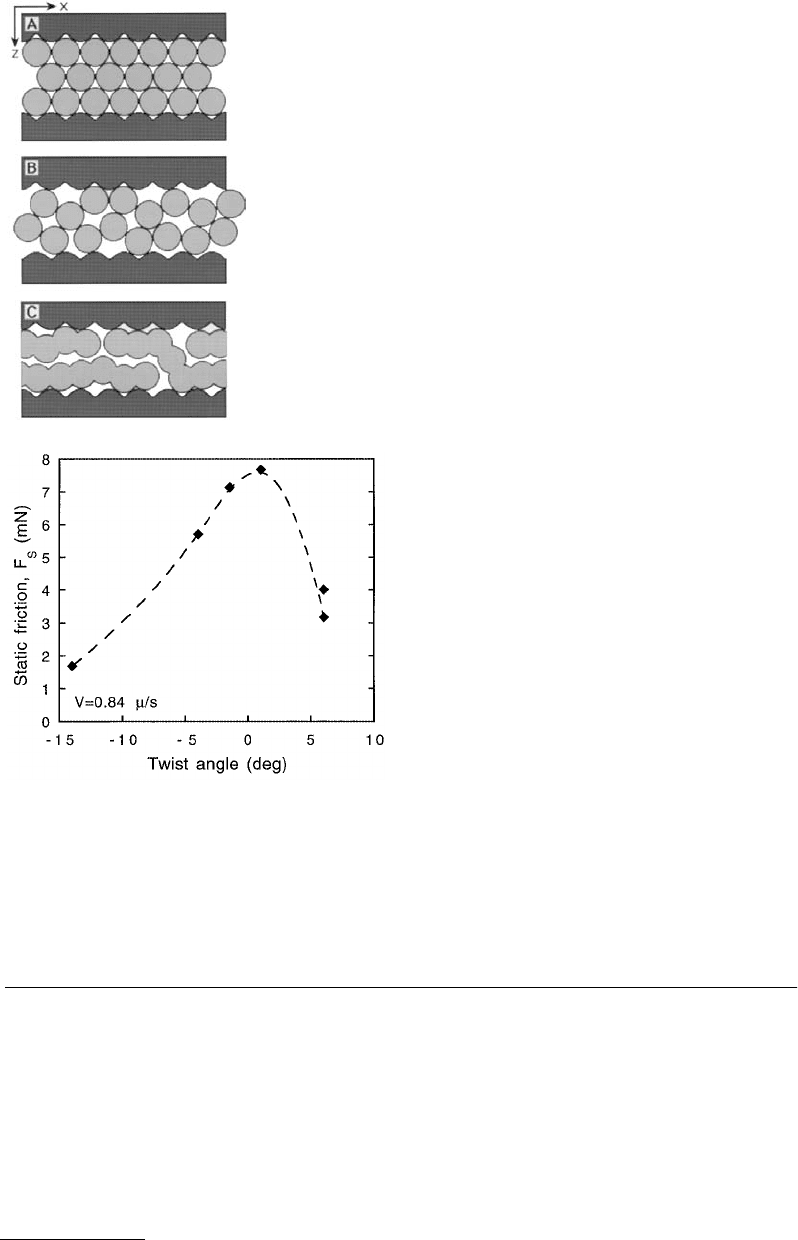
Experiments have demonstrated the effects of surface lattice mismatch on the friction between surfaces

(Hirano et al., 1991; Berman, 1996). Similar to the effects of lattice mismatch on adhesion (Figure 9.5,

Section 9.4.1), the static friction of a conﬁned liquid ﬁlm is maximum when the lattices of the conﬁning

surfaces are aligned. For OMCTS conﬁned between mica surfaces (Berman, 1996) the static friction was

found to vary by more than a factor of 4 (Figure 9.28), while for bare mica surfaces the variation was by

a factor of 3.5 (Hirano et al., 1991). In contrast to the sharp variations in adhesion energy over small

twist angles, the variations in friction as a function of twist angle were much more broad — both in

magnitude and angular spread. Similar variations in friction as a function of twist or misﬁt angles have

also been observed in computer simulations (Gyalog and Thomas, 1997).

With rough surfaces, i.e., those that have random protrusions rather than being periodically structured,

we expect a smearing out of the correlated intermolecular interactions that are involved in ﬁlm freezing

and melting (and in phase transitions in general). This should effectively eliminate the highly regular

eff

= FD Av

stick-slip and may also affect the location of the slipping planes. The stick-slip friction of “real” surfaces,

which are generally rough, may therefore be quite different from those of perfectly smooth surfaces

composed of the same material (see next section). We should note, however, that even between rough

surfaces, most of the contacts occur between the tips of microscopic asperities, which may be smooth

over their microscopic contact area.

9.13 Stick-Slip Friction

An understanding of stick-slip is of great practical importance in tribology (Rabinowicz, 1965) since

these spikes are the major cause of damage and wear of moving parts. But stick-slip motion is a much

more common phenomenon and is also the cause of sound generation (the sound of a violin string, a

squeaking door, or the chatter of machinery), sensory perception (taste, texture, and feel), earthquakes,

granular ﬂow, nonuniform ﬂuid ﬂow, such as the “spurting” ﬂow of polymeric liquids, etc. In the previous

section the stick-slip motion arising from freezing–melting transitions in thin interfacial ﬁlms was

described. But there are other mechanisms that can give rise to stick-slip friction, which will now be

considered. However, before proceeding with this, it is important to clarify exactly what one is measuring

during a friction experiment.

FIGURE 9.27 Schematic view of interfacial ﬁlm composed of spherical

molecules under a compressive pressure between two solid crystalline sur-

faces. If the two surface lattices are free to move in the XYZ directions so as

to attain the lowest energy state, they could equilibrate at values of X, Y, and

Z which induce the trapped molecules to become “epitaxially” ordered into

a solidlike ﬁlm. (B) Similar view of trapped molecules between two solid

surfaces that are not free to adjust their positions, for example, as occurs in

capillary pores or in brittle cracks. (C) Similar to (A) but with chain mole-

cules replacing the spherical molecules in the gap. These may not be able to

order as easily as do spherical molecules even if X, Y, and Z can adjust,

resulting in a situation that is more akin to (B).

FIGURE 9.28 Static friction of a 2-nm-thick OMCTS

ﬁlm as a function of the lattice twist angle between the

two conﬁning crystalline mica surfaces. The variation

in friction is comparable to variations in an unlubri-

cated mica–mica system (Hirano et al., 1991).

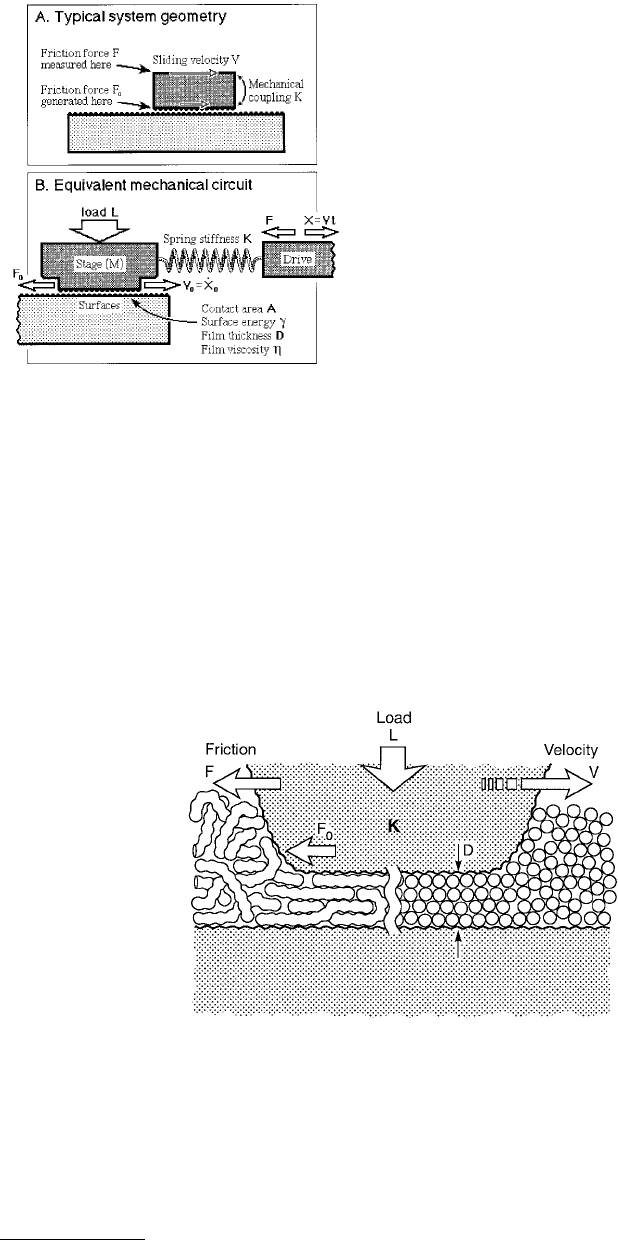
Figure 9.29 shows the basic mechanical coupling and equivalent mechanical circuit characteristic of

most tribological systems and experiments. The distinction between F and F

is important because in

almost all practical cases, the applied, measured, or detected force, F, is not the same as the “real” or

“intrinsic” friction force, F

, generated at the surfaces. F and F

are coupled in a way that depends on

the mechanical construction of the system, for example, the axle of a car wheel which connects it to the

engine. In Figure 9.29A, this coupling is shown to act via the material supporting the upper surface,

which can be modeled (Figure 9.29B) as an elastic spring of stiffness K and mass M. This is the simplest

type of mechanical coupling and is also the same as in SFA and AFM experiments, illustrated in

Figure 9.30. More-complicated real systems can be reduced to a system of springs and dashpots as

described by Luengo et al. (1997).

We now consider four different models of stick-slip friction. These are illustrated in Figures 9.31

through 9.34, where the mechanical couplings are assumed to be of the simple elastic spring type as

FIGURE 9.29 (A) Schematic geometry of two shearing sur-

faces illustrating how the friction force, F

, which is generated

at the surfaces, is generally measured as F at some other place.

The mechanical coupling between the two may be described

in terms of a simple elastic stiffness or compliance, K, or in

terms of more complex nonelastic coefﬁcients, depending on

the system. Here, the mechanical coupling is simply via the

backing material supporting one of the surfaces. (B) Equiva-

lent mechanical circuit for the above setup applicable to most

tribological systems. Note that F

is the force generated at the

surfaces, but that the measured or detected force is F = (X –

)K. The differences between the forces, the velocities and

the displacements at the surfaces and at the drive (or detector)

are illustrated graphically in Figures 9.31 through 9.34.

FIGURE 9.30 (A) Schematic geometry of two contacting asperities separated by a thin liquid ﬁlm. This is also the

geometry adopted in most pin-on-disk, SFA, and AFM experiments. In the SFA experiments described here, typical

experimental values were: undeformed radius of surfaces, R ≈ 1 cm; radius of contact area, r = 10 to 40 µm; ﬁlm

thickness, D ≈ 10Å; externally applied load, L = –10 to +100 mN; measured friction forces, F = 0.001 to 100 mN;

sliding or driving velocity, V = 0.001 to 100 µm/s; surface or interfacial energy, γ = 0 to 30 mJ/m

(erg/cm

); effective

elastic constant of supporting material, K = 10

N/m; elastic constant of friction-measuring spring, K = 500 N/m;

temperature, T = 15 to 40°C.

shown in Figures 9.29 and 9.30. The ﬁrst two mechanisms (Figures 9.31 and 9.33) may be considered as

the “traditional” or “classical” mechanisms or models (Rabinowicz, 1965), the third (Figure 9.34) is

essentially the same as the freezing–melting phase-transition model described in Section 9.12.

9.13.1 Rough Surfaces Model

Rapid slips can occur whenever an asperity on one surface goes over the top of an asperity on the other

surface. As shown in Figure 9.31, the extent of the “slip” will depend on asperity heights and slopes, on

the speed of sliding, and on the elastic compliance of the surfaces and the moving stage. We may note

that, as in all cases of stick-slip motion, the driving velocity (V) may be constant but the resulting motion

at the surfaces (V

) will display large slips as shown in the inset. This type of stick-slip has been described

by Rabinowicz (1965). It will not be of much concern here since it is essentially a noise-type ﬂuctuation,

resulting from surface imperfections rather than from the intrinsic interaction between two surfaces.

Actually, at the atomic level, the regular atomic-scale corrugations of surfaces can lead to periodic stick-

slip motion of the type shown here. This is what is sometimes measured by AFM tips (McClelland, 1989;

McClelland and Cohen, 1990).

9.13.2 Distance-Dependent Model

Another theory of stick-slip, observed in solid-on-solid sliding, is one that involves a characteristic distance

(but also a characteristic time, τ

, this being the characteristic time required for two asperities to increase

their adhesion strength after coming into contact). Originally proposed by Rabinowicz (1958, 1965), this

model suggests that two rough macroscopic surfaces adhere through their microscopic asperities of

characteristic length D

. During shearing, each surface must ﬁrst creep a distance D

— the size of the

contacting junctions — after which the surfaces continue to slide, but with a lower (kinetic) friction force

than the original (static) value. The reason for the decrease in the friction force is that even though, on

average, new asperity junctions should form as rapidly as the old ones break, the time-dependent adhesion

and friction of the new ones will be lower than the old ones. This is illustrated in Figure 9.32.

The friction force therefore remains high during the creep stage of the slip, but once the surfaces have

moved the characteristic distance D

, the friction rapidly drops to the kinetic value. For any system where

the kinetic friction is less than the static force (or one that has a negative slope over some part of its

–V

curve) will exhibit regular stick-slip sliding motion for certain values of K, m, and driving velocity, V.

This type of friction has been observed in a variety of dry (unlubricated) systems such as paper-on-

paper (Baumberger et al., 1994; Heslot et al., 1994) and steel-on-steel (Sampson et al., 1943; Heymann

et al., 1954; Rabinowicz, 1958). This model is also used extensively in geologic systems to analyze rock-

on-rock sliding (Dieterich, 1978, 1979).

FIGURE 9.31 Figures 9.31 through 9.34 show three different models of friction and the stick-slip friction force vs.

time traces they give rise to. Figure 9.31 shows the Rabinowicz model (Rabinowicz, 1965) for rough surfaces which

produces irregular stick-slip (inset) when the elastic stiffness of the system (reﬂected by the slopes of the SLIP lines)

is not too high.

While originally described for adhering macroscopic asperity junctions, the distance-dependent model

may also apply to molecularly smooth surfaces. For example, for polymer lubricant ﬁlms, the character-

istic length D

would now be the chain–chain entanglement length, which could be much larger in a

conﬁned geometry than in the bulk.

9.13.3 Velocity-Dependent Friction Model

This is the most-studied mechanism of stick-slip and, until recently, was considered to be the only cause

of intrinsic stick-slip. If a friction force decreases with increasing sliding velocity, as occurs with boundary

ﬁlms exhibiting shear thinning, the force (F

) needed to initiate motion will be higher than the force (F

)

needed to maintain motion. Such a situation is depicted in Figure 9.33 (Case c), where a decreasing

intrinsic friction force F

with sliding velocity V

results in the sliding surface or stage moving in a periodic

fashion where during each cycle rapid acceleration is followed by rapid deceleration (see curves for X

FIGURE 9.32 Distance-dependent friction model (also known as the creep model) in which a characteristic distance

has to be moved to break adhesive junctions. The model also has a characteristic, τ

, this being the time needed

for the adhesion and friction forces per junction to equilibrate after each contact is made.

and V

in Figure 9.33). So long as the drive continues to move at a ﬁxed velocity V, the surfaces will

continue to move in a periodic fashion punctuated by abrupt stops and starts whose frequency and

amplitude depend not only on the function F

) but also on the stiffness K and mass M of the moving

stage, and on the starting conditions at t = 0.

More precisely, referring to Figures 9.29 and 9.33, the motion of the sliding surface or stage can be

determined by solving the following differential equation:

(9.47)

(9.48)

where F

= F

, V

, t) is the intrinsic or real friction force at the shearing surfaces which is generally a

function of X

, V

and t, F is the force on the spring (the externally applied or measured force), and

= (F

– F) is the force on the stage. To solve fully Equation 9.47, one must also know the initial (starting)

conditions at t = 0, and the driving or steady-state conditions at ﬁnite t. For example, in the present

experiments, the driving condition is

FIGURE 9.33 The lower part of the ﬁgure shows the stage or surface displacement X

, surface velocity V

( = dX

/dt

or X

), and measured friction force F, as functions of time t for surfaces whose intrinsic friction force is F

. In general,

is a function of X

, V

, and t. Three speciﬁc examples are shown here corresponding to F

either increasing

monotonically (Case a), remaining constant (Case b), or decreasing monotonically (Case c) with V

The latter case

corresponds to a ﬁlm that exhibits “shear thinning.” Only when F

) has a negative slope is the resulting motion

of the stick-slip type, characterized by very different motions and friction forces being detected at the surfaces (the

Stage) and the detector (the Drive).

MX F F F X X K

˙˙

00 0 0

=−

()

=− −

()

MX X X K F

˙˙

00 0

0+−

()

−=

(9.49)

In other systems, the appropriate driving condition may be F = constant.

Various forms for F

= F

,t) have been proposed, mainly phenomenological, to explain various

kinds of stick-slip phenomena. These models generally assume a particular functional form for the friction

as a function of velocity only, F

= F

), and they may also contain a number of mechanically coupled

elements comprising the stage (Tomlinson, 1929; Carlson and Langer, 1989).

One version is a two-state

model characterized by two friction forces, F

and F

, which is a simpliﬁed version of the phase-transitions

model (next section). More complicated versions can have a rich F–v spectrum, as proposed by Persson

(1994). Unless the experimental data is very detailed and extensive, these models cannot generally

distinguish between different types of mechanisms. Neither do they address the basic question of the

origin of the friction force, since this is assumed to begin with.

Experimental data have been used to calculate the friction force as a function of velocity within an

individual stick-slip cycle (Nasuno et al., 1997). For a macroscopic granular material conﬁned between

solid surfaces, the data show a velocity-weakening friction force during the ﬁrst half of the slip. However,

the data also show a hysteresis loop in the friction–velocity plot, with a different behavior in the

deceleration half of the slip phase. Similar results were observed for a 1 to 2 nm liquid lubricant ﬁlm

between mica surfaces (Berman, Carlson and Ducker, unpublished results). These results indicate that a

purely velocity-dependent friction law is insufﬁcient to describe such systems, and an additional element

such as the state of the conﬁned material must be considered (next section).

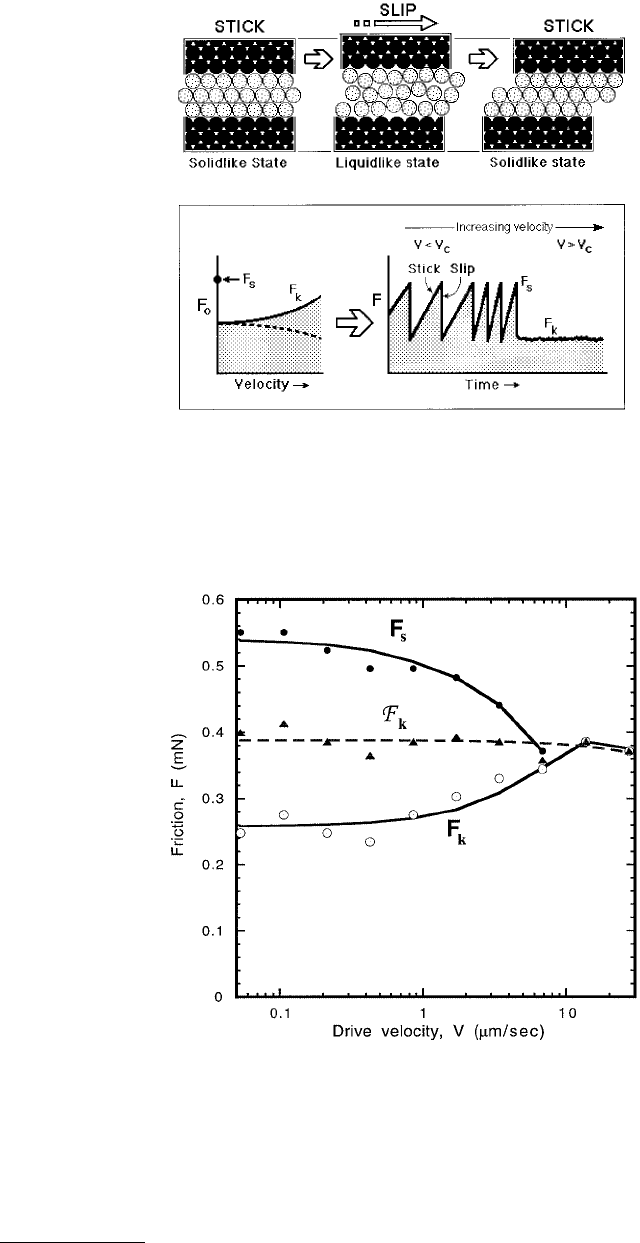
9.13.3 Phase Transitions Model

Recent molecular dynamics computer simulations have found that thin interfacial ﬁlms undergo ﬁrst-

order phase transitions between solidlike and liquidlike states during sliding (Thompson and Robbins,

1990; Robbins and Thompson, 1991) and have suggested this is responsible for the observed stick-slip

behavior of simple isotropic liquids between two solid crystalline surfaces. With this interpretation, stick-

slip is seen to arise because of the abrupt change in the ﬂow properties of a ﬁlm at a transition (Israelachvili

et al., 1990; Thompson et al., 1992) rather than the gradual or continuous change as occurs in the previous

example. Such simulations have accounted for many of the observed properties of shearing liquids in

ultrathin ﬁlms between molecularly smooth surfaces, and have so far offered the most likely explanation

for experimental data on stick-slip friction, such as shown in Figure 9.36.

A novel interpretation of the well-known phenomenon of decreasing coefﬁcient of friction with

increasing sliding velocity has been proposed by Thompson and Robbins (1990) based on their computer

simulation. This postulates that it is not the friction that changes with sliding speed v, but rather the

time various parts of the system spend in the sticking and sliding modes. In other words, at any instant

during sliding, the friction at any local region is always F

or F

, corresponding to the static or kinetic

values. The measured frictional force, however, is the sum of all these discrete values averaged over the

whole contact area. Since as v increases, each local region spends more time in the sliding regime (F

)

and less in the sticking regime (F

) the overall friction coefﬁcient falls. One may note that this interpre-

tation reverses the traditional way that stick-slip has been explained, for rather than invoking a decreasing

friction with velocity to explain stick-slip, it is now the more fundamental stick-slip phenomenon that

is producing the apparent decrease in the friction force with increasing sliding velocity. This approach

has been studied analytically by Carlson and Batista (1996), with a comprehensive rate- and state-

dependent friction force law. This model includes an analytic description of the freezing–melting tran-

sitions of a ﬁlm, resulting in a friction force that is a function of sliding velocity in a natural way. This

model predicts a full range of stick-slip behavior observed experimentally.

An example of the rate- and state-dependent model is observed when shearing thin ﬁlms of OMCTS

between mica surfaces (Berman et al., 1996a,b). In this case the static friction between the surfaces is

dependent on the time that the surfaces are at rest with respect to each other, while the intrinsic kinetic

friction F

is relatively constant over the range of velocities (Figure 9.35). At slow driving velocities, the

XVt t V

=> =

for

for where constant.

FIGURE 9.34 Phase-transition model of stick-slip, for example, where a thin liquid ﬁlm alternately freezes and

melts as it shears, shown here for 22 spherical molecules conﬁned between two solid crystalline surfaces. This model

differs from that of Figure 9.33 in that the intrinsic friction force F

is here assumed to change abruptly (at the

transitions) rather than smoothly or continuously. The resulting stick-slip is also different, for example, the peaks

are sharper and the stick-slip disappears above some critical velocity, V

. Note that while the slip displacement is here

shown to be only two lattice spacings; in most practical situations it is much larger.

FIGURE 9.35 Measured friction F

and F

for increasing drive velocity V with OMCTS conﬁned between two mica

surfaces. F

(solid circles) decreases with increasing velocity because at higher drive speeds the sticking time is shorter,

resulting in less complete freezing of the lubricant layer. The observed F

(open circles) increases as F

decreases,

resulting in a nearly constant intrinsic friction force F

(triangles) ≈ (F

+ F

)/2 for these underdamped conditions.

The critical velocity is reached when F

decreases to the intrinsic friction F

system responds with stick-slip sliding with the surfaces reaching maximum static friction before each

slip event, and the amplitude of the stick-slip, F

– F

, is relatively constant. As the driving velocity

increases, the static friction decreases as the time at relative rest becomes shorter with respect to the

characteristic time of the lubricant ﬁlm. As the static friction decreases with increasing drive velocity, it

eventually equals the intrinsic kinetic friction F

, which deﬁnes the critical velocity V

, above which the

surfaces slide smoothly, without the jerky stick-slip motion.

The above classiﬁcations of stick-slip are not exclusive, and molecular mechanisms of real systems may

exhibit aspects of different models simultaneously. They do, however, provide a convenient classiﬁcation

of existing models and indicate which experimental parameters should be varied to test the different

models.

9.13.4 Critical Velocity for Stick-Slip

For any given set of conditions, stick-slip disappears above some critical sliding velocity V

, above which

the motion continues smoothly in the liquidlike or kinetic state. The critical velocity is found to be well

described by two simple equations. Both are based on the phase-transition model, and both include some

parameter associated with the inertia of the measuring instrument. The ﬁrst equation is based on both

experiments and simple theoretical modeling (Yoshizawa and Israelachvili, 1993):

(9.50)

where τ

is the characteristic nucleation time or freezing time of the ﬁlm. For example, inserting the

following typically measured values for a ~ 10 Å thick hexadecane ﬁlm between mica: (F

– F

) ≈ 5 mN,

spring constant K ≈ 500 N/m, and nucleation time (Yoshizawa and Israelachvili, 1993) τ

≈ 5 s, we obtain

≈ 0.4 µm/s, which is close to typically measured values (Figure 9.36). The second equation is based

on computer simulations (Robbins and Thompson, 1991):

(9.51)

where σ is a molecular dimension and M is the mass of the stage. Again, inserting typical experimental

values into this equation, speciﬁcally, M ≈ 20 gm, σ ≈ 0.5 nm, and (F

– F

) ≈ 5 mN as before, we obtain

≈ 0.3 ∝µm/s, which is also close to measured values.

Stick-slip also disappears above some critical temperature T

, which is not the same as the melting

temperature of the bulk ﬂuid. Certain correlations have been found between V

and T

, and between

various other tribological parameters, that appear to be consistent with the principle of “time-temperature

superposition,” similar to that occurring in viscoelastic polymer ﬂuids (Ferry, 1980).

We end by consid-

ering these correlations.

9.13.5 Dynamic Phase Diagram Representation

of Tribological Parameters

Both friction and adhesion hysteresis vary nonlinearly with temperature, often peaking at some particular

temperature, T

. The temperature dependence of these forces can therefore be represented on a dynamic

phase diagram such as shown in Figure 9.37. Experiments have shown that T

, and the whole bell-shaped

curve, are shifted along the temperature axis (as well as in the vertical direction) in a systematic way

when the load, sliding velocity, etc. are varied. These shifts also appear to be highly correlated with one

another, for example, an increase in temperature producing effects that are similar to decreasing the

sliding speed or load.

≈

−

()

≈

⋅

01.,

∆σ