Biermann Ch. Handbook of Pulping and Papermaking

Подождите немного. Документ загружается.

364 W- PULPING CALCULATIONS

14-

100

Sodium hydrogen sulfide, %

80 60 40 20

12-

DO 8 0

0 10

60 80

100

^ 8-

NaOH from sodium sulfide, % Hydrogen sulfide, %

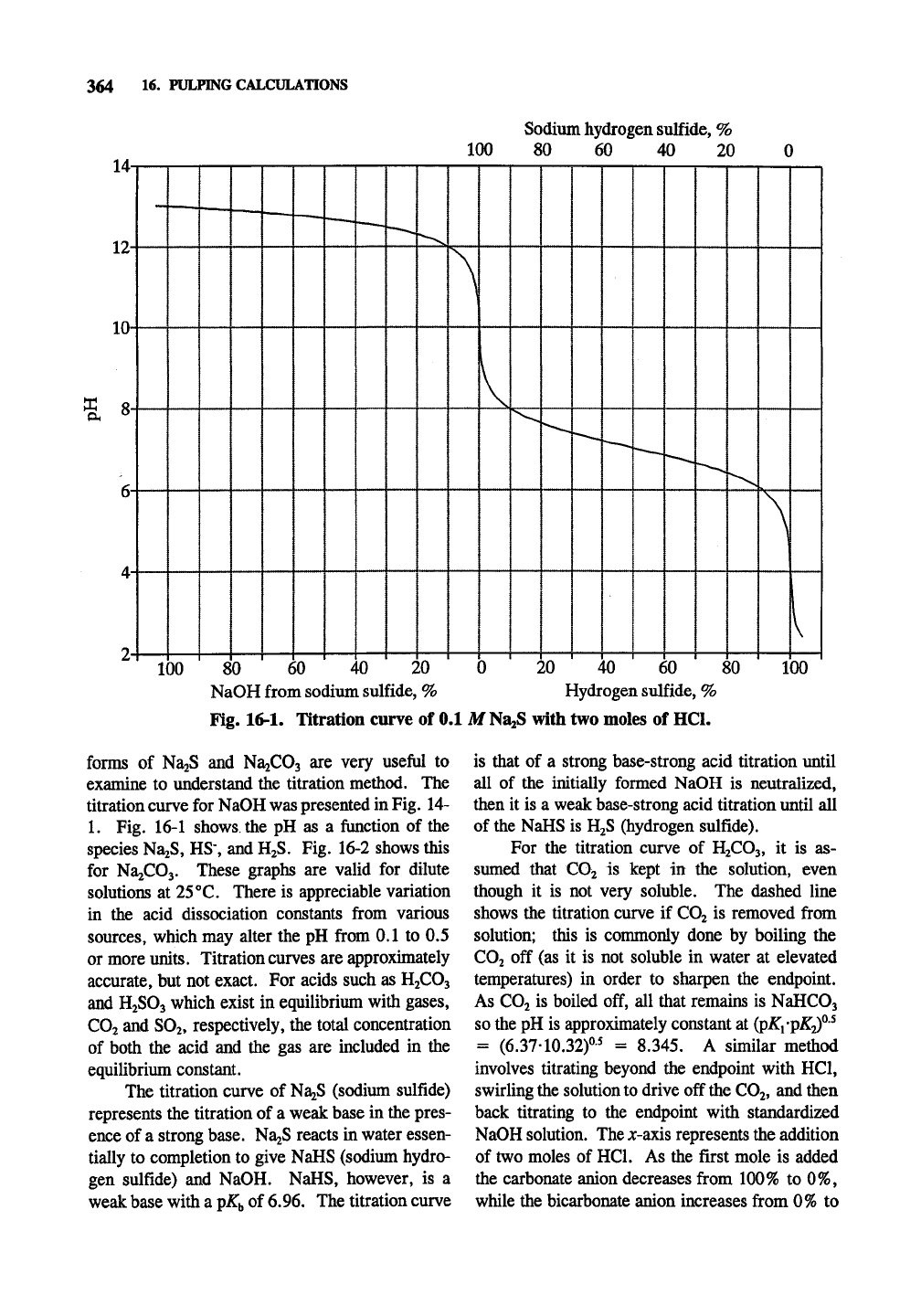
Fig. 16-1. Titration curve of 0.1 M

NaaS

with two moles of HCl.

forms of NajS and NajCOa are very useful to

examine to understand the titration method. The

titration curve for NaOH was presented in

Fig.

14-

Fig. 16-1 shows the pH as a function of the

species NaiS, HS, and

H2S.

Fig. 16-2 shows this

for NajCOj. These graphs are valid for dilute

solutions at 25

^'C.

There is appreciable variation

in the acid dissociation constants from various

sources, which may alter the pH from 0.1 to 0.5

or more units. Titration curves are approximately

accurate, but not exact. For acids such as H2CO3

and H2SO3 which exist in equilibrium with gases,

CO2 and SO2, respectively, the total concentration

of both the acid and the gas are included in the

equilibrium constant.

The titration curve of NajS (sodium sulfide)

represents the titration of a weak base in the pres-

ence of a strong base. Na2S reacts in water essen-

tially to completion to give NaHS (sodium hydro-

gen sulfide) and NaOH. NaHS, however, is a

weak base with a ^K^ of 6.96. The titration curve

is that of a strong base-strong acid titration until

all of the initially formed NaOH is neutralized,

then it is a weak base-strong acid titration until all

of the NaHS is H2S (hydrogen sulfide).

For the titration curve of H2CO3, it is as-

sumed that CO2 is kept in the solution, even

though it is not very soluble. The dashed line

shows the titration curve if CO2 is removed from

solution; this is commonly done by boiling the

CO2 off (as it is not soluble in water at elevated

temperatures) in order to sharpen the endpoint.

As CO2 is boiled off, all that remains is NaHC03

so the pH is approximately constant at (pJ^fpjQ®-^

= (6.37-10.32)«-^ = 8.345. A similar method

involves titrating beyond the endpoint with HCl,

swirling the solution to drive off

the

CO2, and then

back titrating to the endpoint with standardized

NaOH solution. The x-axis represents the addition

of two moles of HCl. As the first mole is added

the carbonate anion decreases from 100% to 0%,

while the bicarbonate anion increases from 0% to

12-

11-

10-

Bicarbonate anion, %

20 40 60 80 100 80 60 40

KRAFT LIQUOR CHENflCAL ANALYSIS 365

20 0

X 1.

100 80 60 40

Carbonate anion, %

20 0 20 40

60 80 100

Carbon dioxide, %

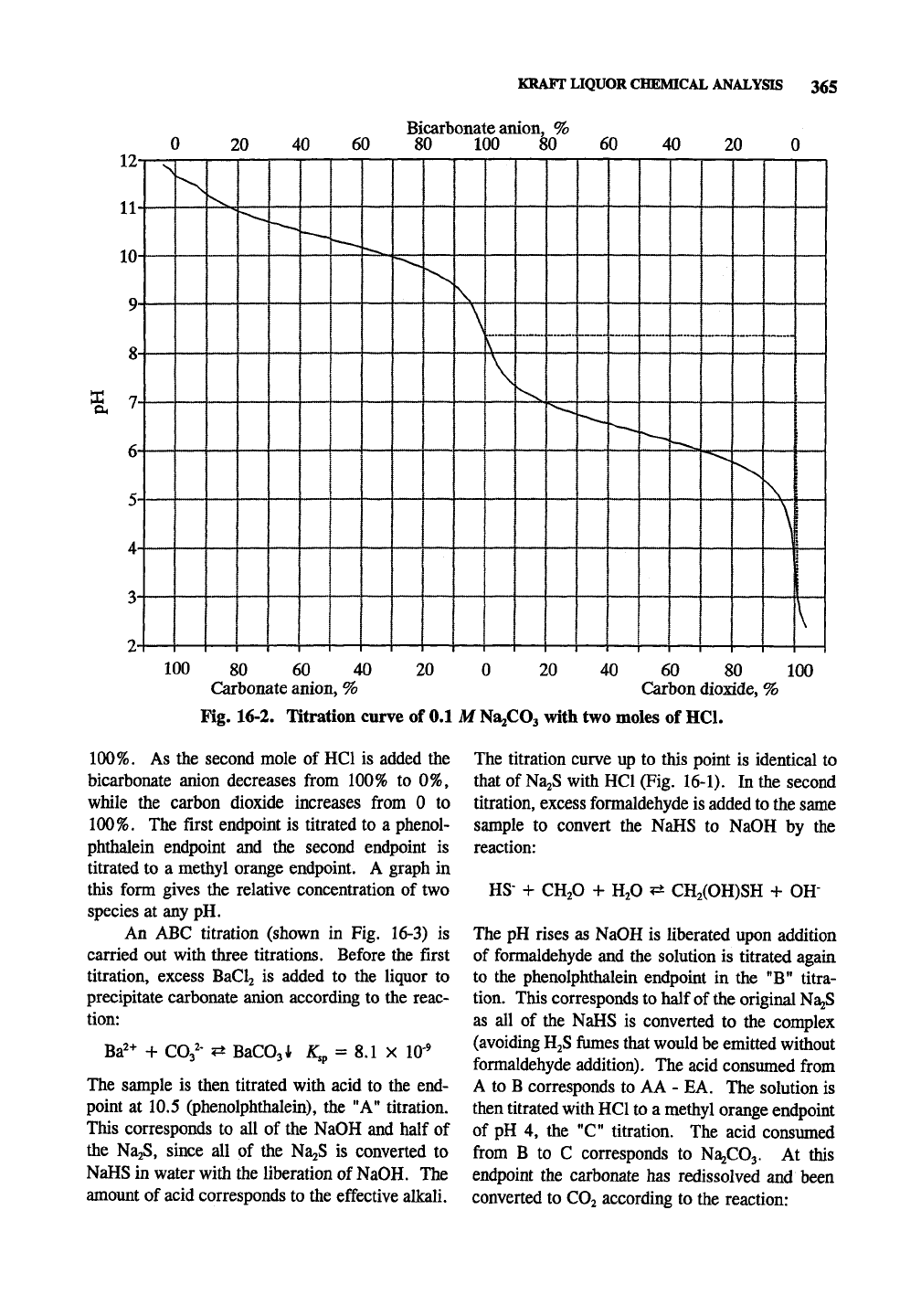
Fig. 16-2. Titration curve of 0.1 M

1^2iflO^

with two moles of HCl.

100%.

As the second mole of HCl is added the

bicarbonate anion decreases from 100% to 0%,

while the carbon dioxide increases from 0 to

100%.

The first endpoint is titrated to a phenol-

phthalein endpoint and the second endpoint is

titrated to a methyl orange endpoint. A graph in

this form gives the relative concentration of two

species at any pH.

An ABC titration (shown in Fig. 16-3) is

carried out with three titrations. Before the first

titration, excess BaCl2 is added to the liquor to

precipitate carbonate anion according to the reac-

tion:

Ba^-^ + CO32- ^ BaCOsi K,^ = 8.1 x 10'^

The sample is then titrated with acid to the end-

point at 10.5 (phenolphthalein), the "A" titration.

This corresponds to all of the NaOH and half of

the NajS, since all of the NajS is converted to

NaHS in water with the liberation of

NaOH.

The

amount of acid corresponds to the effective alkali.

The titration curve up to this point is identical to

that of

Na2S

with HCl (Fig. 16-1). In the second

titration, excess formaldehyde is added to the same

sample to convert the NaHS to NaOH by the

reaction:

HS-

+ CH2O + H2O ^ CH2(0H)SH + OH-

The pH rises as NaOH is liberated upon addition

of formaldehyde and the solution is titrated again

to the phenolphthalein endpoint in the "B" titra-

tion. This corresponds to half of the original NagS

as all of the NaHS is converted to the complex

(avoiding

H2S

fumes that would be emitted without

formaldehyde addition). The acid consumed from

A to B corresponds to AA - EA. The solution is

then titrated with HCl to a methyl orange endpoint

of pH 4, the "C" titration. The acid consumed

from B to C corresponds to NajCOj. At this

endpoint the carbonate has redissolved and been

converted to CO2 according to the reaction:

366 1^. PULPING CALCULATIONS

BaCOsCs) + 2HC1 ^ BaCli + HjO + COjt

To summarize, the significance of A, B, and C are

as follows:

white liquor, it is important to avoid high concen-

trations of acid that might redissolve the BaCOj;

it would probably be better to handle it like black

liquor.

1 TTA

= A

= B

= C

NaOH

H2S

NazCOj

= 2A-B

= 2(B-A)

= C-B \

Black liquor is titrated in a similar fashion if

one is interested in residual concentrations of these

species after the pulping process. One important

difference is that after the BaCl2 is added, the

sample is centrifiiged to collect the precipitate at

the bottom of a test tube. An aliquot is taken

from the supernatant for titration. Otherwise, the

BaCOj interferes with the first two endpoints as it

does not precipitate well. The "C" endpoint must

then be determined on a separate aliquot that has

not been treated with

BaClj.

This brings up the

important point that during an ABC titration of

EXAMPLES. Given:

0.500

iVH2SO4 is used to

titrate 5.00 ml of

white liquor sample. The

titration values were A = 30.6 ml, B = 34.2

ml,

and C = 38.7 ml. Calculate AA, EA,

and TTA.

SOLUTION: Each ml of H2SO4 is equivalent to

0.500

meq/ml X 31 mg NaiO/meq = 15.5

mg NajO. 15.5 mg

N2ijO/5

ml liquor = 3.1

mg NajO/Cml white liquor)/(ml titrant) = 3.1

g/LNajO. Therefore,

EA = 30.6 X 3.1 =94.9g/L

AA = 34.2 X 3.1 = 106 g/L

TTA = 38.7 X 3.1 = 120 g/L

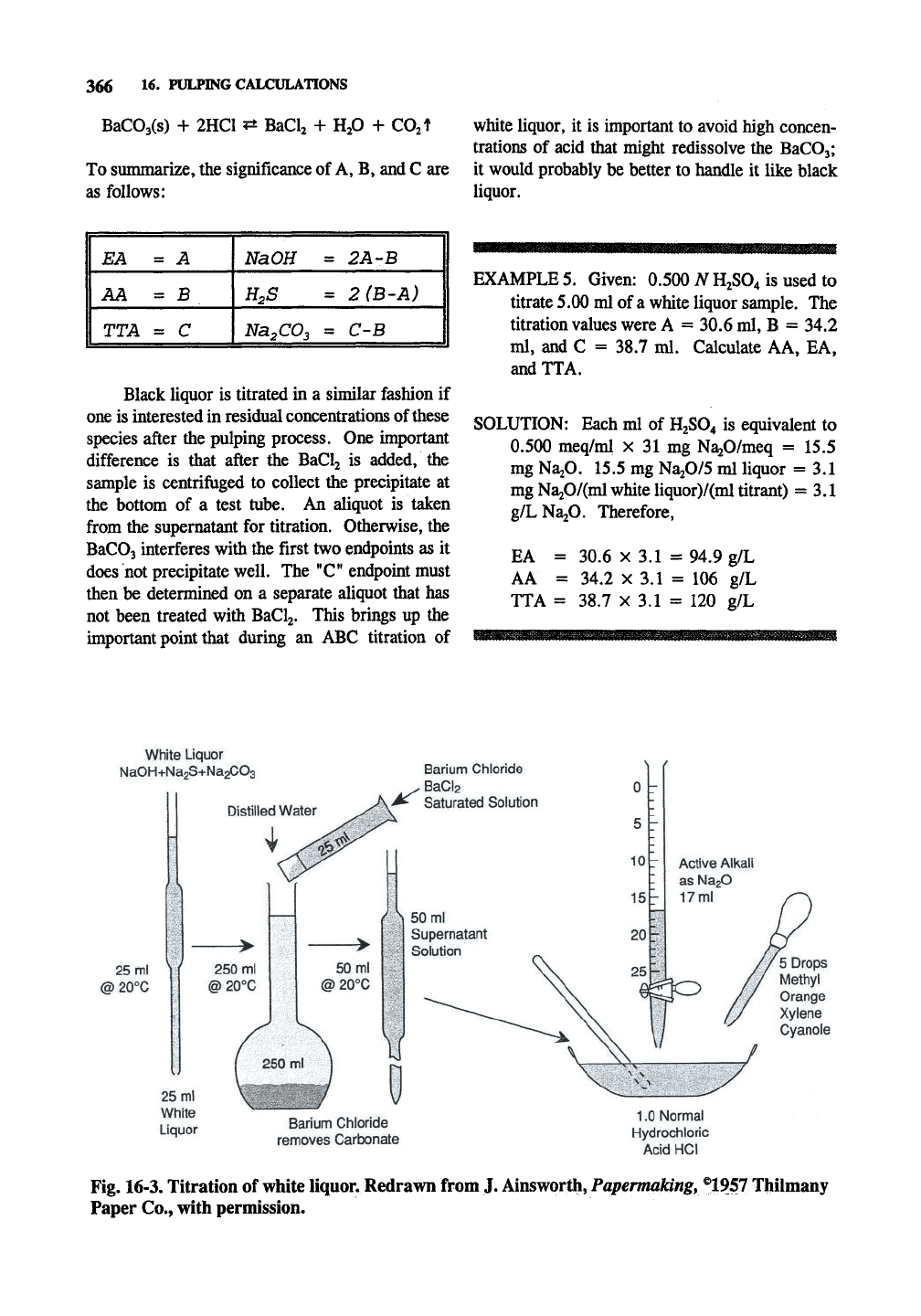
White Liquor

NaOH+NagS+NagCOa

Distilled Water

Barium Chloride

^ BaCl2

v^ Saturated Solution

25 ml

@20°C

25 mi

White

Liquor

Barium Chloride

removes Carbonate

Active Alkali

as NagO

17 ml

5 Drops

Methyl

Orange

Xylene

Cyanole

1.0 Normal

Hydrochloric

Acid HCI

Fig. 16-3. Titration of white liquor. Redrawn from J. Ainsworth, Papermaldng,®195T Thilmany

Paper Co., with permission.

SPECIFIC

GRAVITY AND VISCOSITY OF KRAFT LIQUORS 367

16.4 SPECIFIC GRAVITY AND VIS-

COSITY OF KRAFT LIQUORS

The specific gravity of white liquor at room

temperature may be estimated as follows:

specific gravity = 1.0 + (% solids/100%)

The specific gravities and Baume values as a

function of southern pine kraft black liquor solids

content is given in CPPA data sheet C-5 (issued in

1943,

reissued in 1952, but now apparently aban-

doned; it was at one time TAPPI DATA SHEET

58A).

It should be used with care with other

species; however, it is a good approximation lack-

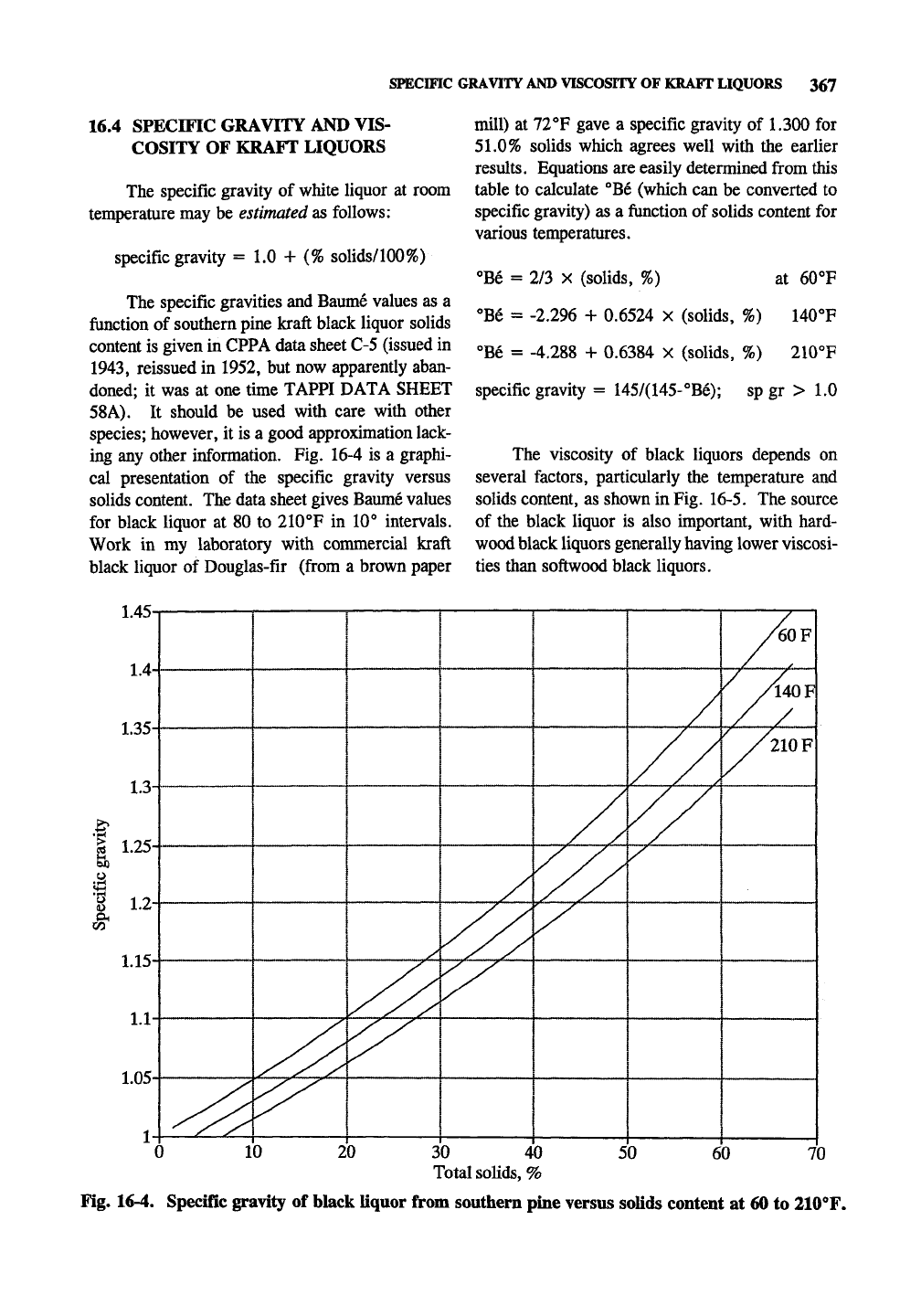
ing any other information. Fig. 16-4 is a graphi-

cal presentation of the specific gravity versus

solids content. The data sheet gives Baume values

for black liquor at 80 to 210°F in 10° intervals.

Work in my laboratory with commercial kraft

black liquor of Douglas-fir (from a brown paper

mill) at 72°F gave a specific gravity of 1.300 for

51.0%

solids which agrees well with the earlier

results. Equations are easily determined from this

table to calculate °Be (which can be converted to

specific gravity) as a function of solids content for

various temperatures.

°Be = 2/3 X (solids, %) at 60°F

°Be = -2.296 + 0.6524 X (solids, %) 140°F

°Be = -4.288 + 0.6384 X (solids, %) 210°F

specific gravity = 145/(145-°Be); sp gr > 1.0

The viscosity of black liquors depends on

several factors, particularly the temperature and

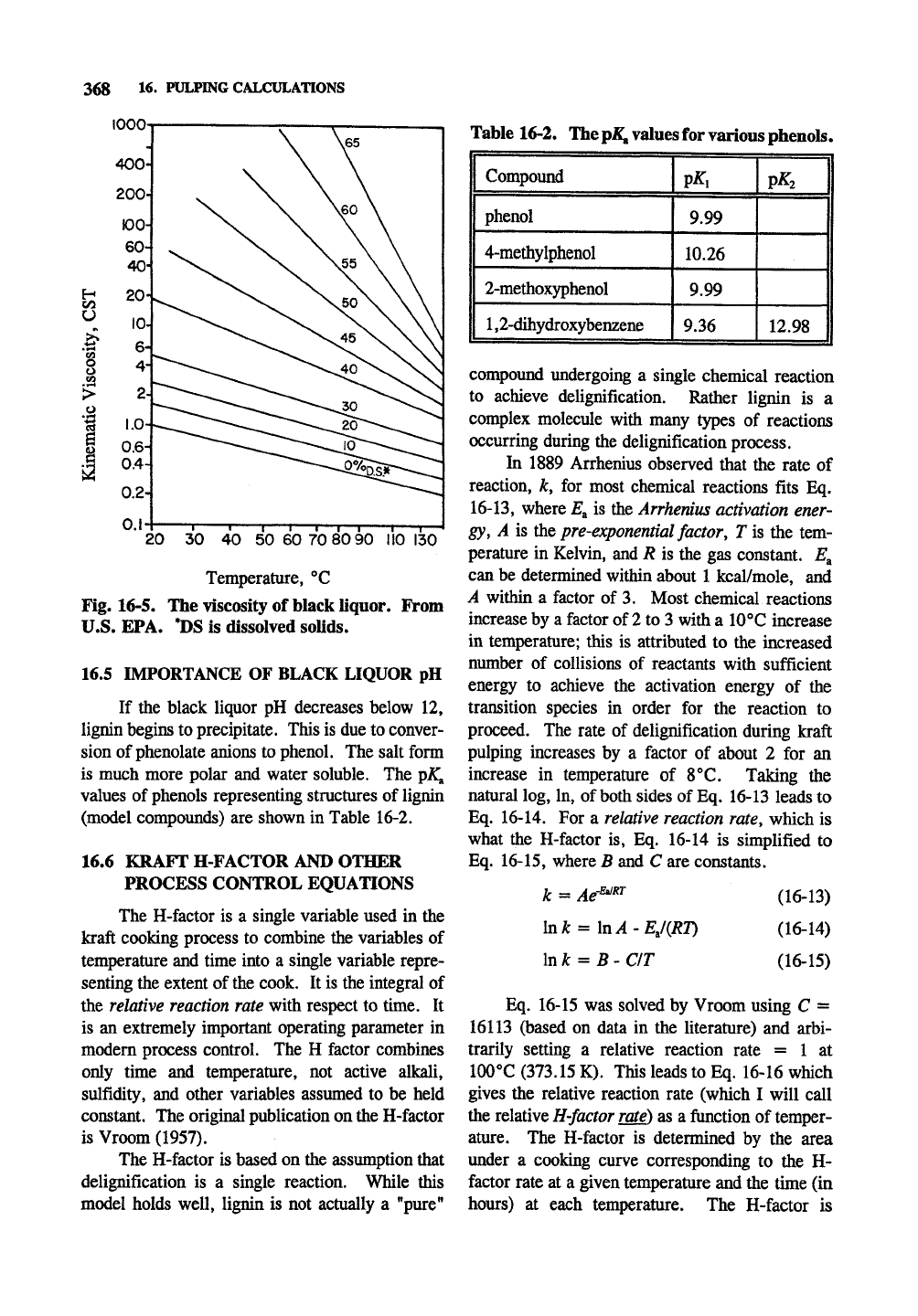
solids content, as shown in Fig. 16-5. The source

of the black liquor is also important, with hard-

wood black liquors generally having lower viscosi-

ties than softwood black liquors.

1.4-

1.3-

I.ZJ-

1 O.

1«^

1 1

«J-

I.ID-

1.1

n^-

1.U3

z:^

XXy

//y

/60F

/140FI

^210

50 60

30 40

Total solids, %

Fig. 16-4. Specific gravity of black liquor from southern pine versus solids content at 60 to llOT.

368 1^- PULPING CALCULATIONS

1000

C/3

•^

400-

200-

100-

60-

40-

20-

10-

1.0-

0.6-

04-

0.2

0.1

Table 16-2.

The

p^,

values

for various phenols.

40 50 60 70 80 90 110 130

Temperature, °C

Fig. 16-5. The viscosity of black liquor. From

U.S. EPA. *DS is dissolved solids.

16.5 IMPORTANCE OF BLACK LIQUOR pH

If the black liquor pH decreases below 12,

lignin begins to precipitate. This is due to conver-

sion of phenolate anions to phenol. The salt form

is much more polar and water soluble. The pJ^^

values of phenols representing structures of lignin

(model compoimds) are shown in Table 16-2.

16.6 KRAFT H-FACTOR AND OTHER

PROCESS CONTROL EQUATIONS

The H-factor is a single variable used in the

kraft cooking process to combine the variables of

temperature and time into a single variable repre-

senting the extent of the cook. It is the integral of

the relative reaction rate with respect to time. It

is an extremely important operating parameter in

modem process control. The H factor combines

only time and temperature, not active alkali,

sulfidity, and other variables assumed to be held

constant. The original publication on the H-factor

is Vroom (1957).

The H-factor is based on the assumption that

delignification is a single reaction. While this

model holds well, lignin is not actually a "pure"

Compound

phenol

4-methylphenol

2-methoxyphenol

1,2-dihydroxybenzene

piST,

9.99

10.26

9.99

9.36

12.98

compound undergoing a single chemical reaction

to achieve delignification. Rather lignin is a

complex molecule with many types of reactions

occurring during the delignification process.

In 1889 Arrhenius observed that the rate of

reaction, k, for most chemical reactions fits Eq.

16-13,

where

is the Arrhenius activation ener-

gy, A is the

pre-exponential

factor, T is the tem-

perature in Kelvin, and R is the gas constant. E^

can be determined within about 1 kcal/mole, and

A within a factor of 3. Most chemical reactions

increase by a factor of 2 to 3 with a 10"^C increase

in temperature; this is attributed to the increased

number of collisions of reactants with sufficient

energy to achieve the activation energy of the

transition species in order for the reaction to

proceed. The rate of delignification during kraft

pulping increases by a factor of about 2 for an

increase in temperature of 8°C. Taking the

natural log. In, of both sides of Eq. 16-13 leads to

Eq. 16-14. For a relative reaction rate, which is

what the H-factor is, Eq. 16-14 is simplified to

Eq. 16-15, where B and C are constants.

k =

Ae-^^"""^

lni;:

= InA'EJiRT)

Ink = B-C/T

(16-13)

(16-14)

(16-15)

Eq. 16-15 was solved by Vroom using C =

16113 (based on data in the literature) and arbi-

trarily setting a relative reaction rate = 1 at

100°C (373.15 K). This leads to Eq. 16-16 which

gives the relative reaction rate (which I will call

the relative H-factor

rate)

as a function of temper-

ature. The H-factor is determined by the area

under a cooking curve corresponding to the H-

factor rate at a given temperature and the time (in

hours) at each temperature. The H-factor is

KRAFT H-FACTOR AND OTHER PROCESS CONTROL VARIABLES 369

2000

1900

1800

1700

1600

1500

1400

1300

^ 1200

I" 1100

^ 1000

900

800

700

600

500

400

300-

200

100

140

145 150 170

175

155 160 165

Temperature, Celsius

Fig. 16-6. The relative H-factor rate/hr as a function of temperature.

180

therefore the integral of the H-factor rate with

respect to time expressed in hours. The relative

H-factor rate is shown as a function of temperature

in Fig. 16-6. Fig 16-7 shows the H-factor rate for

a linear heating temperature ramp from 80-170°C.

In this case the H-factor may be estimated by

using a suitable approximation method, such as the

one explained below. Temperatures below 130**C

(265 °F) contribute very little to the overall extent

of the cook.

lnA: = 43.181-16113/r (16-16)

There are slight discrepancies between calcu-

lated values and values given in Vroom*s paper,

but this is due to the available calculation methods

the

time that Vroom did his work. Also, Vroom

used 100**C = 373 K (obtaining a S of 43.20)

instead of 373.15 K. For 180°C and using B =

43.20,

the H-factor is 2060/hr at 453 K and

2084/hr at 453.15 K (a 1.2% difference) although

Vroom reported it as 2042/hr. I suggest using Eq.

16-16 and adding 273.15 to the temperature in

Celsius for reasonable agreement with Vroom's

published values and to promote a consistent theo-

retical basis. At 170°C this modification gives

917/hr, Vroom's equation gives 923/hr, and

Vroom reported 927/hr. At 160°C this gives

396/hr, Vroom's equation gives 398/hr, and

Vroom reported 401/hr. These differences are

insignificant and presented only to alleviate con-

cern an individual might have when calculating

values that differ from published values.

The H-factor alone cannot be used to predict

the yield or other properties of the pulp. Howev-

er, once the H-factor versus yield relationship (or

other pulping parameter relating to lignin content

such as kappa number) is determined for a partic-

ular set of pulping conditions, the yield for a given

H-factor will be known (presumably) for any time-

370 1^. PULPING CALCULATIONS

temperature combination used to achieve that H-

factor.

EXAMPLE 6. Sawdust is pulped in a continuous

digester at a constant temperature (zero heat-

up time) of 180°C for 45 minutes to a kappa

number of 30. If the digester temperature is

increased by 5°C and the other pulping

conditions are held constant, solve the fol-

lowing:

a) What pulping time is required to reach the

same kappa number?

b) What is the percent increase in digester

output?

Note: the H-factor rate at 180°C = 2042/hr

and at 185°C = 3054/hr

SOLUTION, a) The H-factor of the cook at

180°C is 2042/hr x 0.75 hr = 1532. To

cook to the same H-factor at 185°C, solve

for time as: t = 1532/3054

hr"^

= 0.50 hr =

30 min. Cooking at the higher temperature

gives 3 batches/90 min or a 50% increase in

production.

^^^^M^lM^«l^e^i^^M^'lillli1ll1fl]l!lllililili1lll1l!ill1ll?

Although

Eq.

16-16 enjoys widespread

use

industry, there is no reason to assume that the

activation energy of the Arrhenius equation is the

same for hardwoods and softwoods or even among

species of either group. Furthermore, the compo-

sition of cooking chemical may influence the

activation energy somewhat. Taking the derivative

of the Arrhenius equation and solving for the

activation energy gives Eq. 16-17.

RT^

Ink/dT

RT,T2(AT)-'

HkrSri)

(16-17)

EXAMPLE 7. Solve for

based on the H-

factor relative reaction rates at 165^*0 and

175°C.

SOLUTION. (0.001987 kcal mol'^ K"^) x (438

K)(448 K)(10 K)-^ X ln(1387/610) = 32.0

kcal. Also, comparison of Eq. 16-14 to Eq.

16-16 shows that 16113 = EJR; therefore,

= 32.0 kcal/mole and is independent of

temperature.

Often linear temperature ramps are used or

assumed during digester heating. It would be

ideal to integrate Eq. 16-16 with respect to time

using a linear temperature ramp to solve for the

H-factor during the heat-up time. By integrating

from absolute zero the form of the equation could

be written as follows, where T, is the rate of

temperature increase.

H-factor =

mdt =

-^^''''

J ^-^^iiwr') f

Leta = -16113/rr and^: = 1/r so,

dx =

-r^dt;

the integral is now in this form:

H-factor = C

ef^lx"

Unfortunately this integral leads to a series

that requires several hundred terms before diverg-

ing, due to the large value of a, involving num-

bers on the order of 100! (factorial), making it

more difficult to solve than "manual" methods.

Below is a short program listed in BASIC which

can be used to solve the H-factor for linear tem-

perature ramps (or any ramp with suitable modifi-

cation). The program is set up for a temperature

ramp of 80-170°C during 90 minutes. Rimning

the program as is (with 6 time intervals of 15

minutes gives an H-factor of approximately 165.4

for the time period. Fig. 16-7 is a graphic depic-

tion of what the program accomplishes. The

program works by dividing the temperature inter-

val defined by the final temperature, TF, and

initial temperature, TI, into rectangles of time.

The reaction rate is determined at the temperature

corresponding to the center of the time interval

and applied to the entire time interval to give an

H-factor for that rectangle, TOTAL. The more

rectangles used, the closer the approximation.

Using 10 time intervals gives an H-factor of

171.6, while using 900 time intervals gives 175.2;

obviously only a few intervals are needed for

sufficient accuracy.

KRAFT H-FACTOR AND OTHER PROCESS CONTROL VARIABLES 371

800

Fig. 16-7.

under the

80 90

40 50

Time, Minutes

A linear heating ramp from 80-170''C with an approximation of H-factor by the area

curve as rectangles.

10 TI = 80

20 TF = 170

25 TIME = 90

30 REM REMARK STP IS THE WIDTH OF

THE RECTANGLES IN DEGREES

(WHICH IS CONVERTED TO TIME),

AND INCR IS THE AREA OF EACH

RECTANGLE. BE SURE TO THAT THE

NUMBER OF DEGREES IN THE TEM-

PERATURE RAMP IS EVENLY DIVISI-

BLE BY STP.

40 STP = 15

50 FOR I = TI TO (TF-STP) STEP STP

60 INCR = EXP(43.181-(16113/(273.15 + I +

0.5 * STP)))

70 TOTAL = TOTAL + (INCR*

(STP/((TF-TI)/(TIME/60))))

80 NEXT I

90 PRINT TOTAL

Empirical equations have been published

which have found uses in process control. Hatton

(1973,

1976) discusses many of these and presents

his own model for pulp yield and kappa number.

His equation of pulp yield is in the form of the

equation: Yield = A - B[(log J9)(EA)"], where

EA is the effective alkali and H is the H-factor.

The coefficients were solved for a variety of

different species of both hardwoods and soft-

woods. Generally, the softwoods had much higher

correlation coefficients.

Edwards and Norberg (1973) developed an

extension of the H-factor called the r (tau) factor,

which is a single variable combining the effects of

time,

temperature, initial EA, and liquor to wood

ratio.

Earlier work had established the T factor

concept for hypochlorite and chlorine dioxide

bleaching data. At constant sulfidity, r =

(EA/L:W)^H. Lin et al. (1978) calculated the

kappa number as a function of H-factor, liquor to

wood ratio, and alkali to wood ratio, obtaining a

single equation for hardwoods of Taiwan and the

Ivory Coast. Tasman (1981) calculated the yield

as a function of the liquor sulfidity, effective

alkali, and the H-factor for several species of

hardwoods and softwoods in his equations. Re-

cently, Paulonis and Krishnagopalan (1991) dis-

cussed a sophisticated process control system for

kraft batch digesters that uses liquid density,

electrical conductivity, and other techniques in

addition to the usual parameters in order to predict

kappa number despite variations in wood chip

supply and digester operation.

Kubes et al. (1983) have developed a G-

372 16. PULPING CALCULATIONS

Table 16-3. The H-factor rate, G-factor rate,

and ratio for various temperatures.

Temp.,"’C

160

165

170

175

180

H-fact.

400

610

927

1387

2042

G-fact.

2960

5220

9100

15600

29600

HIG ratio

0.135

0.117

0.102

0.089

0.069

factor that is analogous to the H-factor except that

remaining cellulose viscosity is correlated to

cooking temperature and time under constant

conditions for any alkaline cooking process. The

method works for any alkaline method since

cellulose viscosity loss is due to random alkaline

cleavage, and there are no known additives that

decrease this reaction. While one may not expect

viscosity to be correlated to extent of reaction, the

authors' model fits the data fairly well. The

authors obtain the value of 175-180 kJ/mol for this

reaction.

Table 16-3 lists the H-factor rate, G-factor

rate,

and ratio of H-factor to G-factor rates at

various temperatures. The higher this ratio, the

less cellulose viscosity decrease is predicted when

cooking to a specified kappa number. Table 16-3

indicates that cooking at 160°C would give pulp

with twice the viscosity as pulp cooked at 180°C.

16.7 SULFITE LIQUOR CALCULATIONS

The concentrations of chemicals in sulfite

pulping are reported on an

SO2

basis. This allows

the various forms of sulfurous acid and its salts to

be compared on an equal molar basis, although the

concentrations are reported on a weight basis.

(This is the same principle as using NajO as the

basis for kraft pulping and recovery chemicals.)

The concentration is reported as a percent or

g/100 ml, both of which are identical units if the

specific gravity is unity. Full chemical sulfite

methods all use approximately

20%

chemical (SO2

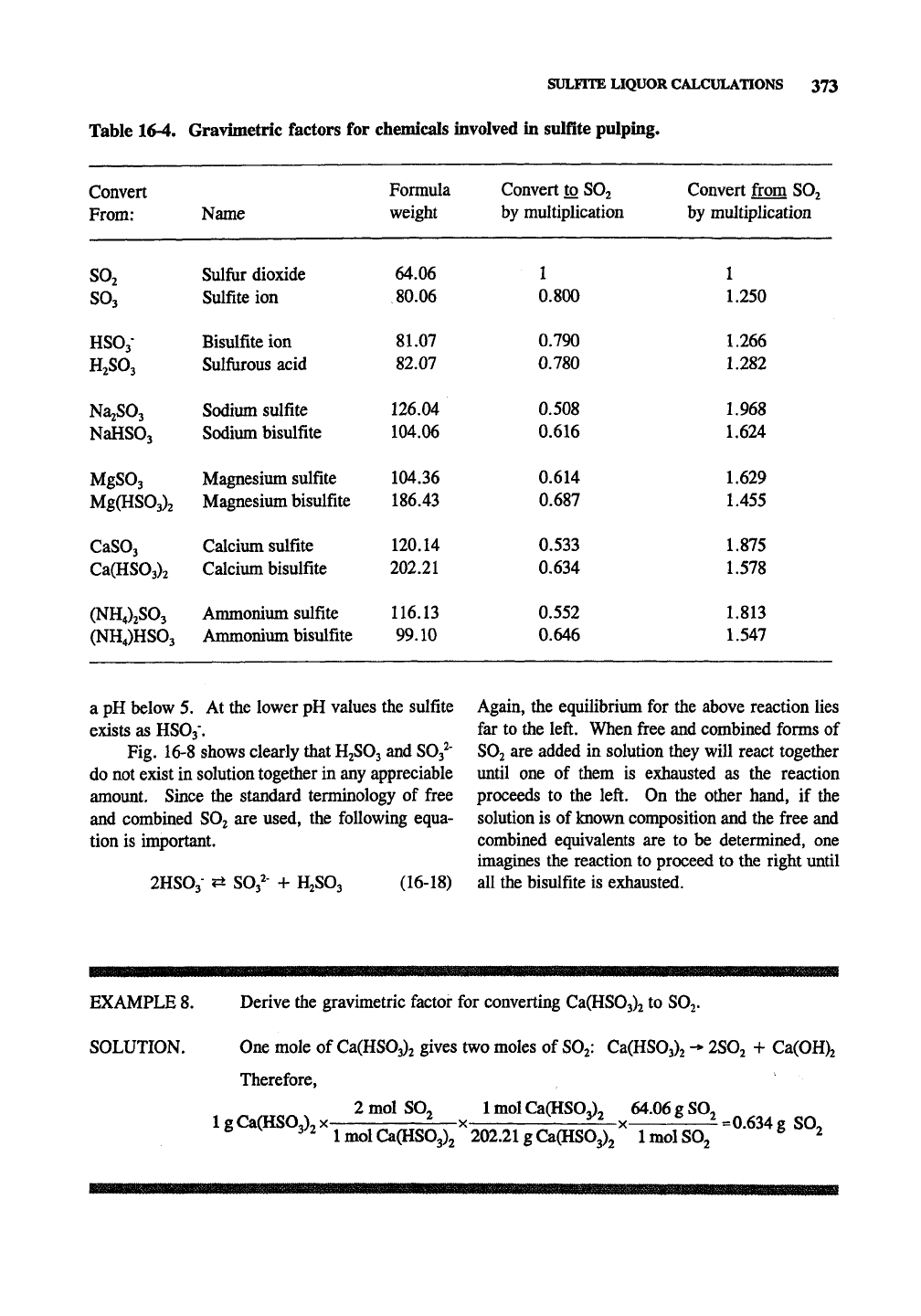
basis) on a dry wood basis. Table 16-4 gives

conversion factors to and from the actual chemical

concentrations and the

SO2

basis. See Example 8

to see how these conversion factors are derived.

The various sahs of sulfurous acid are of

central importance to the various sulfite-based

processes. The chemistry of sulfurous acid as a

function of

is very important. For the titration

curve of

H2SO3,

the first proton is a moderately

strong acid and titrates along with any strong acids

present. Therefore no initial "endpoint" below 0

ml base (corresponding to excess acid) is present

as there is for a weaker acid such as acetic acid.

The Henderson-Hasselbalch equation cannot be

used for this part of the titration curve since the

H2SO3 ionizes appreciably, thereby reducing the

concentration of

H2SO3

and changing the ratio of

acid to conjugate base significantly. The quadratic

equation must be used to solve [H"^] for the initial

part of the titration curve. After about 40 ml of

NaOH is added, the pH is calculated accurately by

this equation.

It is assumed that

SO2

is kept in the solution,

even though it is only partially soluble at room

temperature. The

A:-axis

represents the addition of

two moles of NaOH. As the first mole is added

the SO2 decreases from 100% to 0% while the

bisulfite anion increases from 0% to 100%. As

the second mole of NaOH is added the bisulfite

anion decreases from 100% to 0% while the

sulfite ion increases from 0 to 100%.

The ionization of sulfurous acid is tempera-

ture dependent. Rydholm, in Pulping Processes,

456, gives the ^K^ as 1.8 at 25^*0, 2.3 at 70°,

2.6 at 100°, 3.0 at 120°, and 3.3 at 140°C.

Sulfurous acid is a moderately strong acid.

It will react completely with any of the five com-

mon hydroxides used in sulfite cooking. The form

of the reaction is independent of the base and

occurs in two steps if enough base is present.

MOH + H2SO3

T±

MHSO3 + H2O

MOH + MHSO3 ^ M2SO3 4- H2O

M is ViMg^^,

ViCd^^,

Na-', NH4+, or K"'

Since CaS03 has limited solubility (^^p = 6.8

10*

at 25°C), calcium based sulfite cooking has

to be carried out at a pH of 1-2 to maintain

SO2

the soluble

HS03'.

Similarly, since MgS03 has a

limited solubility {K,^ = 3.2 x 10"^ at 25°C),

magnesium based sulfite cooking is carried out at

SULFITE LIQUOR CALCULATIONS 373

Table 16-4. Graviiiietric factors for chemicals involved in sulfite pulping.

Convert

From:

SO2

SO3

HSOj-

H2SO3

Na^SOj

NaHSOj

MgSOj

Mg(HS03)2

CaSOj

Ca(HS03)2

(NH4)jS03

(NH4)HS03

Name

Sulfur dioxide

Sulfite ion

Bisulfite ion

Sulfiirous acid

Sodium sulfite

Sodium bisulfite

Magnesium sulfite

Magnesium bisulfite

Calcium sulfite

Calcium bisulfite

Ammonium sulfite

Ammonium bisulfite

Formula

weight

64.06

80.06

81.07

82.07

126.04

104.06

104.36

186.43

120.14

202.21

116.13

99.10

Convert to SOj

by multiplication

0.800

0.790

0.780

0.508

0.616

0.614

0.687

0.533

0.634

0.552

0.646

Convert fi-om SO2

by multiplication

1.250

1.266

1.282

1.968

1.624

1.629

1.455

1.875

1.578

1.813

1.547

a pH below 5. At the lower pH values the sulfite

exists as HSOs".

Fig. 16-8 shows clearly that

H2SO3

and SOj^-

do not exist in solution together in any appreciable

amount. Since the standard terminology of free

and combined SOj are used, the following equa-

tion is important.

2HSO3-

<^ SO32- + H2SO3

(16-18)

Again, the equilibrium for the above reaction lies

far to the left. When free and combined forms of

SO2 are added in solution they will react together

until one of them is exhausted as the reaction

proceeds to the left. On the other hand, if the

solution is of known composition and the free and

combined equivalents are to be determined, one

imagines the reaction to proceed to the right until

all the bisulfite is exhausted.

EXAMPLE 8. Derive the gravimetric factor for converting Ca(HS03)2 to SOj.

SOLUTION. One mole of Ca(HS03)2 gives two moles of

SOj:

Ca(HS03)2 -* 2SO2 + Ca(0H)2

Therefore,

lgCa(HS03)2x

2 mol SO.

mol Ca(HSOA 64.06 g SO,

—X ^^ ^^^x —?-=0.634 g SO,

ImolCaOHSOj)^ 202.21 g Ca(HS03)2 ImolSO^ ^ ^