Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


12. exp (x
2
)
13. ln (x 1 1)
14. (x
2
2 1)(x 1 5)
15. (x 1 1)/(x 2 1)
16. x/(22x)
17. 27(x
2
1 1)
5/3
18. x sin (x)
19. x cos (2x)
20. tan (x)
21. 2
x
22. x/3
x
23. e
x
sin (x)
24. 2
x
cos (3x)
25. log
3
(x)
26. x log
2
(x)
c In Exercises 2736, calculate the requested derivative. b
27. f
(5)
(x) where f (x) 5 sin (x)
28.
d
2
f
dx
2
where f (x) 5
x
2
x 2 1
29.
€
g(1) where g(t) 5 (3t
2
2 2)
24
30. f
000
(π/6) where f (t) 5 sin (t) 1 cos (2t)
31. H
(4)
(x) where H(x) 52x
6
1 7x
5
2 9x
2
1 11
32.
d
2
f
dx
2
where f ðxÞ5 sec ð5xÞ
33. f
000
(x) where f (x) 5 cos (4x 1 3)
34.
d
3
dt
3
(t
25/3
1 4t
4
2 8t
7/2
)
35. g
00
(π/6) where g( x) 5 cos (π sin (x))
36. H
(2)
(π/4) where H(x) 5 x tan (x)
c In Exercises 3740, a velocity υ(t)
is given. Calculate the
acceleration (in m/s
2
). b
37. υ(t) 5 24
m/s
38. υ(t) 5 t
2
2 5t m/s
39. υ(t)5216t 1 5 m/s
40. υ(t) 5 8e
2t/2
m/s
c In Exercises 4144, a position p(t)
is given. Calculate the
acceleration (in m/s
2
). b
41. p(t) 5 15 1 24t m
42. p(t) 5 3
sin (2t)m
43. p(t) 5 3t
2
1 16t m
44. p(t) 5 10 2 3e
22t
m
45. The position of a bicycle at time t (measured in minutes)
is p(t) 5 2t
3
1 t
2
1 6t meters for 0 , t , 10. What is the
acceleration of the bicycle at time t 5 3s? At time t 5 6s?
46. The position of a moving body is described by p(t) 5
at
2
1 bt 1 c.Ifp(0) 5 3, then what is c?Ifp
0
(0) 5 6, then
what is b?Ifp
00
(0) 525, then what is a? Where is the
body at time t 5 6?
c Exercises 4750 concern an object that is propelled
straight
up. Its height at time t seconds is given in feet by
H(t) 5216t
2
1 128t 1 68. b
47. Compute
the velocity and acceleration of the object.
48. For how many seconds does the object rise?
49. What is the maximum height of the object?
50. Supposing that the trajectory is such that the object is
able to fall to the ground (height 0 feet), for how many
seconds does the object fall?
51. An object is thrown straight down. Its height at time t
seconds is given in feet by H(t) 5216t
2
2 160t 1 84. With
what velocity does it impact the earth (at height 0).
c Exercises 5254 are concerned with a car’s advance p(t)
during
its period of deceleration. Suppose that during the
first t seconds of braking, the car moved forward p(t) 5
48t 2 3t
2
2t
3
/2 ft. Suppose also that this formula was in effect
until the car came to a stop. b
52. What
was the car’s velocity at the moment brakes were
applied?
53. What was its acceleration a(t) at time t? (The negative
sign of a( t) means that the car was decelerating.)
54. How long was the period of deceleration?
Further Theory and Practice
55. Let
f ðxÞ5
x
3
if x . 0
2 x
3
if x # 0:
a. Prove that f
0
(0) exists and equals 0.
b. Prove that f
00
(0) exists and equals 0.
c. Prove that f
000
(0) does not exist.
56. Suppose that f and g are twice differentiable. Calculate a
formula for ( f/g)
00
.
57. Suppose that p(x) is a nonzero polynomial. Prove that
p(x) has degree precisely k if and only if
a. p
(k11)
(x) 5 0 for all x; and
b. p
(k)
(x
0
) 6¼0 for some x
0
.
58. Find an explicit formula for the polynomial p(x)of
degree 2 such that p(0) 5 2, p
0
(0) 5 4, and p
00
(0)527.
59. Find an explicit formula for the polynomial p(x)of
degree 3 such that p(1) 5 1, p
0
(2) 522, p
00
(21)5214, and
p
000
(5) 5 6.
60. Suppose that p(x) is a polynomial, and | p
00
(x)|#1 for all x.
Prove that p is of degree at most 2, and the coefficient of
its degree 2 term is less than or equal to 1/2 in absolute
value.
c In each of Exercises 6166, use equation (3.7.2) to com-
pute
the requested derivative. b
61. D
2
( f g)(x) where f (x) 5 x
2
and g(x) 5 cos (x)
62.
d
2
dx
2
ðx
ffiffiffiffiffiffiffiffiffiffiffi
x 1 1
p
Þ
63. ( f g)
00
(x) where f (x) 5 1/x and g(x) 5 ln (x)
64. D
2
( f g)(x) where f (x) 5 x
3
and g(x) 5 cos (x)
3.7 Higher Derivatives 235

65. ( f g )
(2)
(x) where f (x) 5
ffiffiffi
x
p
and g(x) 5 exp (x)
66.
d
2
dx
2
ðx 1 3Þ
2
ð2x 1 1Þ
3
67. Suppose that f is twice differentiable at c. Show that the
graphs of y 5 f ( x) and y 5 f (c) 1 f
0
ðcÞ(x2c) 1 f
00
(c)
(x2c)
2
/2 both pass through the point (c, f (c)) and have
the same tangent line there.
c Exercises 6873 involve the factorial numbers n !,
which
were introduced in Section 1.4. They can be defined by 0! 5 1
and, for a positive integer n, n! 5 n(n 2 1) ... 3... 2 1. b
68. Let n be
a positive integer. If k is a positive integer no
greater than n, then the expression
n
k
5
n!
k!ðn 2 kÞ!
5
nðn 2 1Þðn 2 2Þ ðn 2 k 1 1Þ
k ðk 2 1Þ 3 2 1
is called a binomial coefficient. For example, if n 5 7, and
k 5 3, then n2k 1 155, and
7
3
5
7 6 5
3 2 1
5 35:
By definition
n
0
5 1. Leibniz’s Rule states that ( f g)
(n)
(c)
is the sum of the n 1 1 expressions that are obtained
by substituting k 5 0, 1, 2, . . . , n in the formula
n
k
f
(n2k)
(c) g
(k)
(c). Explicitly write out Leibniz’s
Rule for n 5 1, 2, and 3. Observe that the n 5 1 case is the
Product Rule, the n 5 2 case is equation (3.7.2). Verify
Leibniz’s Rule for n 5 2.
69. The Legendre polynomials P
n
, introduced in 1782 by
A.M. Legendre, can be defined by the following formula,
which was discovered by Benjamin Olinde Rodrigues
(17941850 or 1851):
P
n
ðxÞ5
1
2
n
n!
d
n
dx
n
ðx
2
21Þ
n
n 5 0; 1; 2; 3;: : : :
Calculate P
0
(x), P
1
(x), P
2
(x), P
3
(x), and P
4
(x).
70. In general, the Legendre polynomial P
n
(x) (as defined in
the preceding exercise) satisfies the differential equation
ð1 2 x
2
ÞP
00
n
ðxÞ2 2xP
0
n
ðxÞ1 nðn 1 1ÞP
n
ðxÞ5 0:
Verify this equation for P
5
(x) 5 (63x
5
2 70x
3
1 15x)/8.
71. For each nonnegative integer n, the Hermite polynomial
H
n
is defined by
H
n
ðxÞ5 ð21Þ
n
e
x
2
d
n
dx
n
e
2x
2
:
Calculate H
0
(x), H
1
(x), H
2
(x), H
3
(x), and H
4
(x).
72. In general, the Hermite polynomial H
n
(x) (as defined in
the preceding exercise) satisfies the differential equation
H
00
n
ðxÞ2 2xH
0
n
ðxÞ1 2nH
n
ðxÞ5 0:
Verify this equation for H
5
(x) 5 32x
5
2 160x
3
1 120x.
73. Prove that any polynomial p(x) of degree k satisfies
pðxÞ5 pð0Þ1 p
0
ð0Þx 1
p
00
ð0Þ
2!
x
2
1 1
p
ðkÞ
ð0Þ
k!
x
k
74. Show that there is a polynomial p (x) of degree n 1 1 such
that
d
n
dx
n
tanðxÞ5 pðtanðxÞÞ:
75. Let p(x) be a polynomial. We say that p has a root of
order k at a if there is a polynomial q such that p(x) 5
(x 2 a)
k
q(x) and q (a) 6¼ 0. Prove that p has a root of
order 2 at x 5 a if and only if p(a) 5 0, p
0
(a) 5 0, and
p
00
(a) 6¼0. (In general, p has a root of order k at a if and
only if p(a) 5 p
0
(a) 5 p
(k21)
(a) 5 0 and p
(k)
(a) 6¼ 0.)
76. Let f ðxÞ5
x
150
1 x
100
6
1 x
93
1 x
90
1 16
42
: Compute
f
(83)
(0). (Hint: Simple observations go farther than brute
force.)
77. Suppose that f is invertible and twice differentiable, that
f (c) 5 γ, and that f
0
(c) 6¼ 0. Show that
ðf
21
Þ
00
ðγÞ52
f
00
ðcÞ
ðf
0
ðcÞÞ
3
78. Verify that
yðtÞ5 h 1 t
ffiffiffi
g
κ
r
2
1
κ
ln
1 1 expð2t
ffiffiffiffiffiffi
gκ
p
Þ
2
satisfies the differential equation
y
00
ðtÞ52g 1 kðy
0
ðtÞÞ
2
:
Calculator/Computer Exercises
c In Exercises 7982, you are given a function f, a value c,
and a viewing rectangle R containing the point P 5 (c, f (c)).
In R, graph the four functions f, g, h, and k, where g(x) 5
f (c) 1 f
0
(c)(x 2 c), h(x) 5 g(x) 1
1
/
2 f
00
(c)(x 2 c)
2
, and k(x) 5
h(x) 1
1
/
6 f w(c)(x 2 c)
3
. The graphs of g, h, and k are,
respectively, linear, parabolic, and cubic approximations of
the graph of f near c. The method of constructing these
approximating functions, which are called Taylor polynomials
of f with base point c, is studied in Chapter 8. b
79. f ðxÞ5
ffiffiffi
ffi
x;
p
c 5 0:5; R 5 ½0; 1 3 ½0; 1:1
80. f (x) 5 x
3/2
, c 5 1, R 5 [0, 4] 3 [21/2, 9]
81. f (x) 5 sin
2
(x), c 5 π/3, R 5 [0, 2] 3 [20.2, 1.2]
82. f (x) 5 xe
x
, c 5 1, R 5 [0, 2] 3 [22.7, 14.8]
c In Exercises 8386, use second central difference quo-
tients
to approximate f
00
(c) to four decimal places. b
83. f ðxÞ5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
x 1 1=x
p
; c 5 e
85. f ðxÞ5 lnð
ffiffiffi
x
p
1 1=
ffiffiffi
x
p
Þ; c 5 3
86. f (x) 5 tan
sin
2
(x)
, c 5 π/4
236 Chapter 3 The Derivative
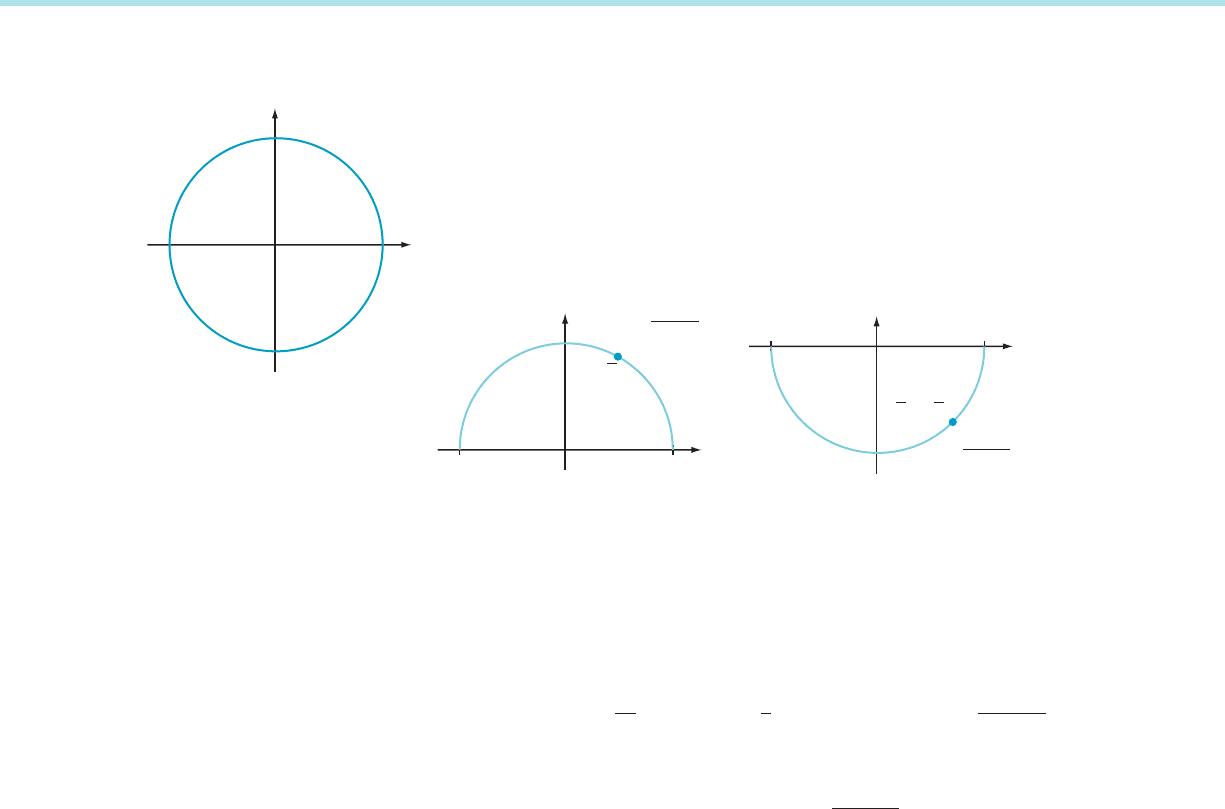
3.8 Implicit Differentiation
Examine the locus of the circle x
2
1y
2
5 4 in Figure 1. We know that, at each point
of the graph, there is a tangent line to the curve. However, we cannot calculate the
equation of the tangent line using the techniques of calculus that we have learned
so far because the circle is not the graph of a function. One way to remedy this
problem is to solve for y in terms of x. We obtain two curves: the upper half of the
circle, which is the graph of y 51
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
, and the lower half of the circle, which is
the graph of y 52
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
. Thus we have realized the circle as the union of the
graphs of two functions. Refer to Figure 2.
Finding the slope of the tangent line to the circle at the point P 5 (1,
ffiffiffi
3
p
) is just
the same as finding the slope of the tangent line to the graph of f ( x ) 51
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
at
P. Similarly, finding the tangent line to the graph of x
2
1 y
2
5 4atQ 5 (
ffiffiffi
2
p
; 2
ffiffiffi
2
p
)
is just the same as finding the slope of the tangent line to the graph of the function
g(x) 52
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
. Differentiating using the Chain RulePower Rule, we find that
f
0
ðxÞ 5
d
dx
ð4 2 x
2
Þ
1=2
5
1
2
ð4 2 x
2
Þ
21=2
ð2 2xÞ5
2 x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
and
g
0
ðxÞ 52f
0
ðxÞ5
x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
Because f
0
(1) 521/
ffiffiffi
3
p
and g
0
(
ffiffiffi
2
p
) 5 1, the slopes of the tangent lines to the circle
at (1,
ffiffiffi
3
p
) and (
ffiffiffi
2
p
, 2
ffiffiffi
2
p
) are 21/
ffiffiffi
3
p
and 1, respectively.
It turns out that there is a simpler way to handle the graph of an equation that
does not express y explicitly as a function of x. Called the method of implicit
differentiation, this technique eliminates the need to solve for y in terms of x.
The Main Idea of
Implicit Differentiation
The example x
2
1 y
2
5 4 that we have been considering suggests a framework for
the general problem we wish to investigate. Because the expression x
2
1 y
2
depends
on the variables x and y, we may write it as F(x,y), using the notation for functions
of two variables (Section 1.4). The right side of x
2
1 y
2
5 4 is a constant, which we
may represent by C. Thus x
2
1 y
2
5 4 is an example of an equation that has the form
F(x, y) 5 C.
It should be understood that, when we write F(x, y), the two variables x and y
are independent variables. Assigning a value to one of them has no bearing on the
y
x
22
2
2
x
2
y
2
4
m Figure 1
y
x
22
2
f(x) 4 x
2
(1, 3)
m Figure 2
y
x
22
2
g(x) 4 x
2
( 2, 2)
3.8 Implicit Differentiation 237

value of the other. Thus if we set x 5 1inF (x, y) 5 x
2
1 y
2
, the equation F (1, y) 5
1 1 y
2
imposes no restriction on the value of y, which clearly is not a funct ion of x.
The matter is quite different when the equation F(x, y) 5 C holds. For example,
setting x 5 1 in the equation x
2
1 y
2
5 4 forces y to be
ffiffiffi
3
p
if (x, y) lies on the upper
semicircle and 2
ffiffiffi
3
p
if (x, y) lies on the lower semicircle. This suggests that, on each
of the two semicircles, y is a function of x. Indeed, as we have already noticed,
we can solve for y and obtain explicit formulas, y 5 f (x) 5
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
and y 5
g(x) 52
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
, for y in terms of x.
In general, we cannot obtain an explicit expression for y from an equation of
the form F(x, y) 5 C. Instead, we understand the equation F(x, y) 5 C to implicitly
define y as a function of x. It may seem impossible to obtain an expression for dy/dx
if we do not have a formula for y, but we can find dy/dx, if it exists, by differ-
entiating each side of the equation F(x, y) 5 C with respect to x. When we do this,
we treat y as though it were a differentiable function of x on an open interval
centered at x
0
. This is the method of implicit differentiation.
Some Examples In illustrating the method of implicit differentiation, we will use Leibniz notation
because it contains a built-in reminder of the variable with respect to which we
differentiate.
⁄ EX
AMPLE 1 Use the method of implicit differentiation to find the slopes
of the tangent lines to the curve x
2
1 y
2
5 4 at the points (1,
ffiffiffi
3
p
) and (
ffiffiffi
2
p
, 2
ffiffiffi
2
p
).
Solution We
apply d/ dx to both sides of the equation. Remembering to treat y as
though it were a function of x, we have
d
dx
ðx
2
1 y
2
Þ5
d
dx
ð4Þ
or
2x
dx
dx
1 2y
dy
dx
5 0
Take particular notic e that we have applied the Chain RulePower Rule to the
first term, even though this was not strictly necessary. There was no need to write
dx
dx
, but in doing so, we have made our treatment of the term x
2
just the same as our
treatment of the term y
2
. As we work our first examples, this will lead to less
confusion. Because dx/dx 5 1, our equation becomes
2x 1 2y
dy
dx
5 0
or
ð2yÞ
dy
dx
522x:
We may solve for dy/dx by dividing both sides by 2y if y 6¼0. The result is
dy
dx
52
x
y
if y 6¼ 0:
238 Chapter 3 The Derivative

Now it is a sim ple matter to find the slope of the tangent line to the curve at
(1,
ffiffiffi
3
p
), for at this point we have
dy
dx
52
x
y
52
1
ffiffiffi
3
p
:
This is the same answer that we obtained in the introduction, but the technique is
easier.
Similarly, we find the slope of the tangent line to the curve at (
ffiffiffiffi
2;
p
2
ffiffiffi
2
p
)tobe
dy
dx
52
x
y
52
ffiffiffi
2
p
2
ffiffiffi
2
p
5 1: ¥
INSIGHT
Compare Example 1 with the discussion at the beginning of this section.
Notice that the method of implicit differentiation does not require separate consideration
of the two functions f (x) 5
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
and g(x) 52
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
whose graphs make up the
curve x
2
1 y
2
5 4.
Knowing how to use the method of implicit differentiation includes knowing when
the method cannot be applied. There are a number of reasons why
dy
dx
P
0
may fail to exist at a point P
0
5 (x
0
, y
0
) on the graph of F(x, y) 5 C. In using the method
of implicit differentiation, we assume that y is a function of x on an open interval
centered at x
0
. This may not actually be the case. In the case of the circle x
2
1 y
2
5 4,
when P
0
5 (22, 0) or P
0
5 (2, 0), neither x
0
522 nor x
0
5 2 is the center of an x2interval
on which y is defined. Even if y is a function of x on an interval centered at x
0
, it may
happen that y is not differentiable with respect to x at P
0
. This occurs if there is no
tangent line at P
0
or if the tangent line exists but is vertical.
Implicit differentiation always expresses the derivative dy/dx as a fraction involving x
or y or both. The points on the curve where the numerator of this fraction is nonzero but
where the denominator is zero correspond to places where the tangent line is vertical or
where it fails to exist. (No simple rule is available for points at which both the numerator
and denominator are zero.)
⁄ EXAMPLE 2 At what points on the curve (y 2 1)
3
1 y(x 2 2) 5 does dy/dx
not exist?
Solution If
we differentiate the equ ation (y 2 1)
3
1 y(x 2 2) 5 0 implicitly with
respect to x, using the Chain RulePower Rule for the first summand and the
Product Rule for the second, then we obtain
3ðy 2 1Þ
2
dy
dx
1
dy
dx
ðx 2 2Þ1 y ð1 2 0Þ5 0 ;
or
3ðy 2 1Þ
2
1 ðx 2 2Þ
dy
dx
52y:
Thus if 3(y 2 1)
2
1 (x 2 2) 6¼ 0, the derivative dy/dx exists and
3.8 Implicit Differentiation 239
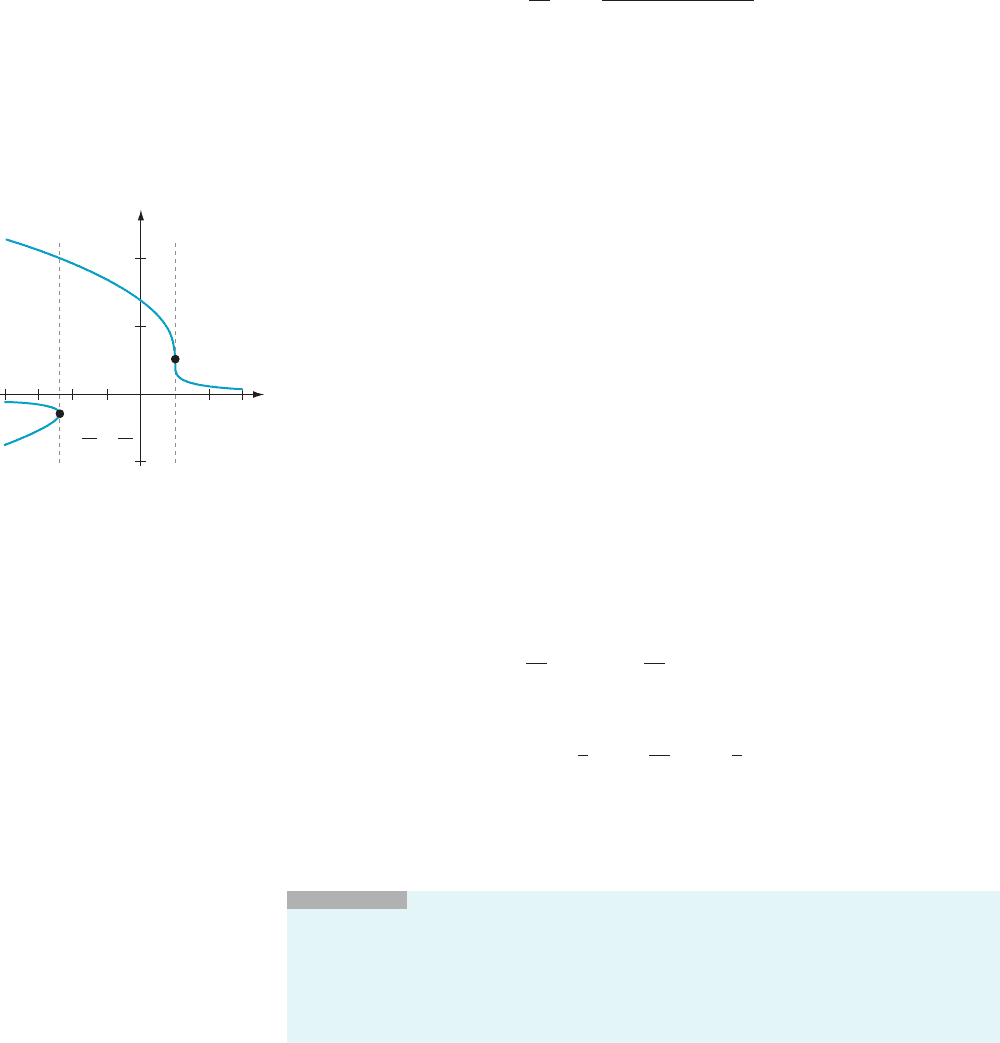
dy
dx
52
y
3ðy21Þ
2
1 ðx 2 2Þ
: ð3:8:1Þ
We must investigate the points (x, y) that satisfy the equations
3ðy 2 1Þ
2
1 ðx 2 2 Þ5 0 ð3:8:2Þ
(because equation (3.8.1) is not valid at such points) and
ðy 2 1Þ
3
1 yðx 2 2Þ5 0 ð3:8:3Þ
(because we consi der only points on the given curve). Equation (3.8.2) gives us
x 2 2 523 ðy21Þ
2
: ð3:8:4Þ
Substituting this formula for x 2 2 into equation (3.8.3) results in (y 2 1)
3
2 3y
(y 2 1)
2
5 0. Factoring, we obtain (y 2 1)
2
(y 2 1 2 3y) 5 0, or (y 2 1)
2
(2y 1 1) 5 0.
The solutions to this last equation are y 5 1, and y 521/2. Substi tuting these values
back into (3.8.4) allows us to determine that x 5 2 when y 5 1, and x 5219/4 when
y 521/2. We have graphed portions of the curve (y 2 1)
3
1 y(x 2 2) 5 0 in Figure 3.
We see that, although y is a function of x near the point (2, 1), dy/dx fails to exist
because the tangent line is vertical. On the other hand, we cannot even define y as a
continuous function of x on an open interval containing 219/4 with the graph of y
passing through the point (219/4, 21/2). Therefore dy/dx has no meaning at this
point.
¥
⁄ EXAMPLE 3 Find the slope of the tangent line to the curve 8 xy
9/2
5 9 2 x
27/5
at the point (1, 1).
Solution Using
implicit differentiation, we have
d
dx
ð8xy
9=2
Þ5
d
dx
ð9 2 x
27=5
Þ;
or, by using the Product Rule and the Chain Rule Power Rule on the left side,
8y
9=2
1 8x
9
2
y
7=2
dy
dx
5 0 1
7
5
x
212=5
:
To make the algebra simpler, we will substitut e in the point (1,1) into this equation
before we solve for dy=dx (but notice that we have finished differentiating). We
obtain 8 1 36 dy/dx 5 7/5, or dy/dx 5211/60.
¥
INSIGHT
You might have noticed that the equation considered in Example 3 is not
of the form F(x, y) 5 C, as specified in the method of implicit differentiation. Although it
would have been easy to rearrange the equation as 8xy
9/2
1 x
27/5
5 9, which does have
the standard form F(x, y) 5 C, it is not necessary to bring all variables to one side of the
equation in order to use the method of implicit differentiation. We may differentiate
the equation as it is presented.
⁄ EXAMPLE 4 Find the equation of the tangent line to the curve
xy
4
1 x 5 17 ð3:8:5Þ
at each point where x 5 1.
(y 1)
3
y(x 2) 0
4 2
4
2
(2,1)
4
6
2
1
2
19
4
,
()
y
x
m Figure 3
240 Chapter
3 The Derivative
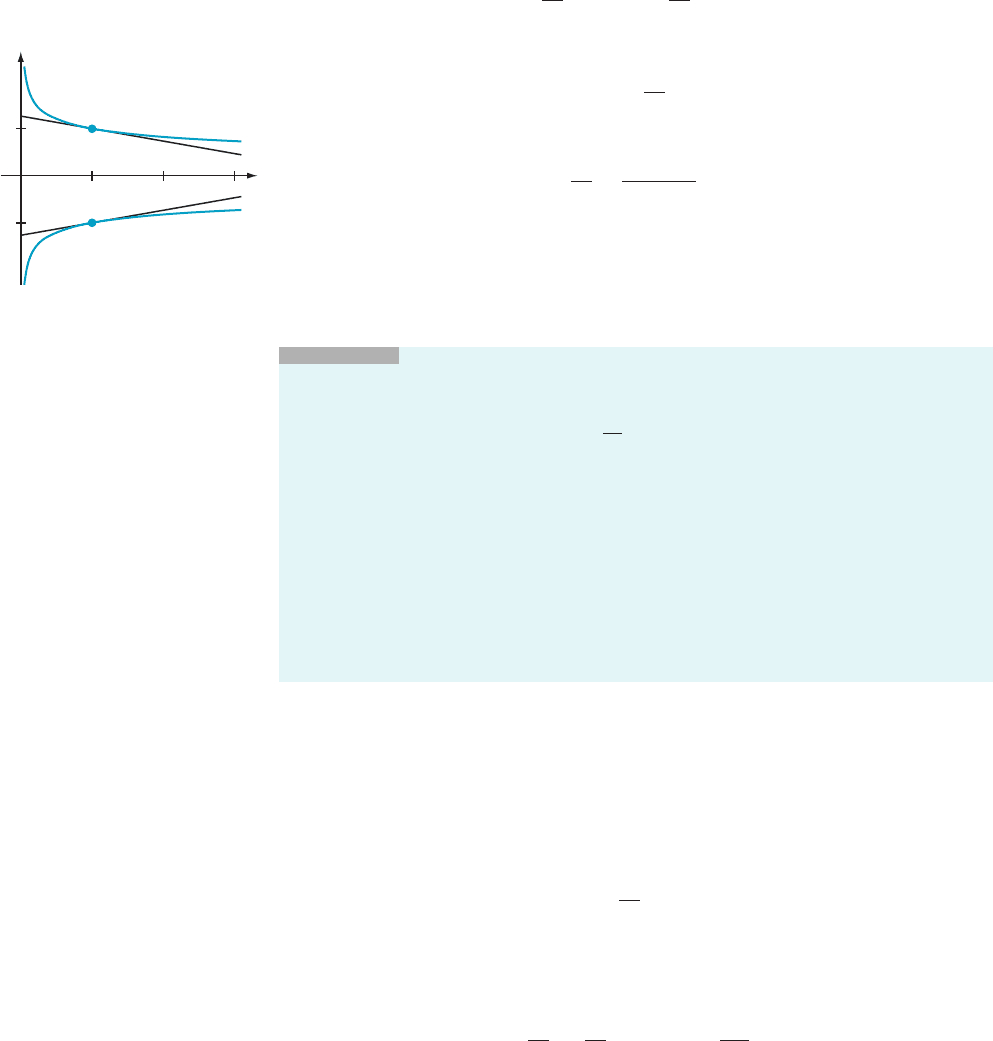
Solution If we substitute x 5 1 into the equation, then we obtain y
4
1 1 5 17. This
simplifies to y
4
5 16 or y 562. Thus there are two points, (1, 2) and (1, 22), with
x 5 1. Now we differentiate equation (3.8.5) to obtain
d
dx
ðxy
4
1 xÞ5
d
dx
ð17Þ:
Performing the different iations, we have
y
4
1 x 4y
3
dy
dx
1 1 5 0;
or
dy
dx
5
2 1 2 y
4
4xy
3
Thus at the point (1, 2), the tangent line has slope 217/32; whereas, at the point
(1,22), the tangent line has slope 17/32. The equations of these tangent lines are
y 5 (217/32) (x 2 1) 1 2 and y 5 (17/32) (x 2 1) 1 (22), respectively. The curve
and its tangents are illustrated in Figure 4.
¥
INSIGHT
When we apply the method of implicit differentiation to find the slope of
the tangent line to F(x, y) 5 C at (x
0
, y
0
), the expression for
dy
dx
ðx
0
;y
0
Þ
will, in general, involve y
0
as well as x
0
. As we see in Example 4, there may be more
than one y for a given x
0
such that (x
0
, y) is on the curve. The value of dy/dx will depend
on which value of y is used. Geometrically, this corresponds to the vertical line x 5 x
0
intersecting the curve F(x, y) 5 C in more than one point. The tangents to the curve at
these points need not be parallel, which is why the value of y sometimes must be specified
when we calculate dy/dx by the method of implicit differentiation. This is unlike the
situation for the explicitly defined functions that we considered prior to this section.
When y is defined as an explicit function of x with x
0
in its domain, the vertical line x 5 x
0
intersects the curve in only one point, and dy/dx is determined by x
0
alone.
Calculating Higher
Derivatives
We can use the metho d of implicit differentiation to calculate higher derivatives.
⁄ EX
AMPLE 5 Consider the equation sin (y) 1 x 5 1/
ffiffiffi
2
p
. Calculate d
2
y/dx
2
at the point (0, π/4).
Solution Diffe
rentiating both sides with respect to x yields
cosðyÞ
dy
dx
1 1 5 0: ð3:8:6Þ
We do not yet substitute in the coordinates of the point we wish to study. We must
differentiate another time. Using the Product Rule to differentiate the first sum-
mand on the left side of equation (3.8.6), we obtain
2 sinðyÞ:
dy
dx
dy
dx
1 cosðyÞ
d
2
y
dx
2
1 0 5 0: ð3:8:7Þ
x
y
2
2
3
xy
4
x 17
xy
4
x 17
y (1732)(x 1) 2
y (1732)(x 1) (2)
(1, 2)
(1, 2)
m Figure 4
3.8 Implicit Differentiation 241
Now that we have finished differentiating, it is correct to put in our numerical
values: Setting y 5 π/4 in equati on (3.8.6) yields
1
ffiffiffi
2
p
dy
dx
ð0; π=4Þ
1 1 5 0 ;
or
dy
dx
ð0; π=4Þ
52
ffiffiffiffi
2:
p
Now we substitute this value for
dy
dx
; together with x 5 0 and y 5 π/4, into equation
(3.8.7) to obtain
2
1
ffiffiffi
2
p
ð2
ffiffiffi
2
p
Þ
2
1
1
ffiffiffi
2
p
d
2
y
dx
2
ð0; π=4Þ
5 0;
or
d
2
y
dx
2
ð0; π=4Þ
5 2: ¥
INSIGHT
There is a subtlety in going from line (3.8.6) to line (3.8.7). When we
differentiated the term cos (y) dy/dx, we had to apply the Product Rule to this term.
The differentiation of the factor cos (y) then led to another factor of dy/dx while the
differentiation of the factor dy/dx led to a factor of d
2
y/dx
2
. In this step, we must be
careful to keep track of both types of derivative that arise.
Parametric Curves Our focus in this section has been the method of implicit differentiation. Placed in a
broader context, our disc ussion has concerned the calculation of tangent lines
to curves that are not presented in the form y 5 f (x). It is therefore appropriate to
extend that discussion by studying the tangent line problem for parametric curves.
Recall from Section 1.5 that these are curves that have the form x 5 ϕ
1
(t), y 5 ϕ
2
(t).
THEOREM 1
Suppose that ϕ
1
and ϕ
2
are differentiable functions on an interval
I 5 (a, b) and that C 5 {(ϕ
1
(t), ϕ
2
(t)) : a , t , b}. Let P
0
5 (x
0
, y
0
) 5 (ϕ
1
(t
0
), ϕ
2
(t
0
))
for some value t
0
in I. If the parametric equations x 5 ϕ
1
(t), y 5 ϕ
2
(t) determine
y as a differentiable function f of x on an arc of C that extends beyond P
0
on
each side and if ϕ
0
1
(t
0
) 6¼0, then
dy
dx
ðx
0
; y
0
Þ
5
ϕ
0
2
ðt
0
Þ
ϕ
0
1
ðt
0
Þ
: ð3:8:8Þ
Proof. By
hypothesis, ϕ
2
(t) 5 y 5 f (x) 5 f (ϕ
1
(t)) for some differentiable function f
defined on an open interval containing t
0
. Differentiating each side of the equation
ϕ
2
(t) 5 f (ϕ
1
(t)) with respect to t, we obtain ϕ
0
2
(t) 5 f
0
(ϕ
1
(t)) ϕ
0
1
(t). Evaluating
at t 5 t
0
, we have ϕ
0
1
(t
0
) f
0
(ϕ
1
(t
0
)) 5 ϕ
0
2
(t
0
), or ϕ
0
1
(t
0
) f
0
(x
0
) 5 ϕ
0
2
(t
0
). If ϕ
0
1
(t
0
)6¼0,
then
dy
dx
ðx
0
; y
0
Þ
5 f
0
ðx
0
Þ5
ϕ
0
2
ðt
0
Þ
ϕ
0
1
ðt
0
Þ
: ’
242 Chapter 3 The Derivative

⁄ EXAMPLE 6 At the beginning of this section, we determined that the
slope of the tangent line to the graph of x
2
1 y
2
5 4atP 5 (1,
ffiffiffi
3
p
Þ is 21/
ffiffiffi
3
p
. Derive
this result using the parametric equations x 5 2 cos (t), y 5 2 sin (t).
Solution We
may verify that ϕ
1
(t) 5 2 cos (t) and ϕ
2
(t) 5 2 sin (t), then
ϕ
1
2
(t) 1 ϕ
2
2
(t) 5 4 (cos
2
(t) 1 sin
2
(t)) 5 4. Because ϕ
1
(π/3) 5 2 cos (π/3) 5 1 and
ϕ
2
(π/3) 5 2 sin (π/3) 5
ffiffiffi
3
p
, the point P 5 (1,
ffiffiffi
3
p
) corresponds to t
0
5 π/3. Formula
(3.8.8) tells us that the required slope is
dy
dx
ð1;
ffiffi
3
p
Þ
5
ϕ
0
2
ðt
0
Þ
ϕ
0
1
ðt
0
Þ
5
2 cos ðtÞ
22 sin ðtÞ
t5t
0
52
cos ðtÞ
sin ðtÞ
t5π=3
52
cos ðπ=3Þ
sin ðπ=3Þ
52
1
ffiffiffi
3
p
: ¥
INSIGHT
In practice, we often do not give names such as ϕ
1
and ϕ
2
to the functions
that define x and y parametrically. When we forgo the extra notation, formula (3.8.8)
simplifies to the more intuitive (and memorable) equation
dy
dx
5
dy=dt
dx=dt
: ð3:8:9Þ
Thus in Example 6, the parametric equations x 5 2 cos (t) and y 5 2 sin (t) lead to dx/dt 5
22 sin (t), dy/dt 5 2 cos (t), and therefore, by (3.8.9),
dy
dx
5
2 cosðtÞ
2 2 sinðtÞ
52
cosðtÞ
sinðtÞ
:
The result is, of course, the same.
QUICK QUIZ
1. The equation ln (y) 1 4y 2 x 5 1 implicitly defines y 5 f ( x ). What is f (3)?
2. Calculate dy/dx at (2, 1) if exp (y 2 1) 1 y 5 x.
3. Suppose that y
3
1 y 5 10x. Calculate dy/dx and d
2
y/dx
2
when x 5 1.
4. If x 5 t
2
1 1, and y 5 t
3
, calculate dy/dx at (5, 28).
Answers
1. 1 2. 1/2 3. dy/dx 5 10/13
and d
2
y/dx
2
52120/13
3
4. 23
EXERCISES
Problems for Practice
c In each of Exercises 16, y is a function of x. Calculate the
derivative of the given expression with respect to x. (Your
answer should contain the term dy/dx.) b
1. 4y
3/2
2. cos (y)
3. 2x/
ffiffiffi
y
p
4. (y
3
2 1) /y
5. xe
y
6. ln (y)/x
c In each of Exercises 714, use the method of implicit
differentiation
to calculate dy/dx at the point P
0
b
7. xy
2
1 yx
2
5 6 P
0
5 (1, 2)
8. sin (πxy) 2 xy
2
1 2y 5 1 P
0
5 (1, 1)
9. x
3/5
1 4y
3/5
5 12 P
0
5 (32, 1)
10. x
4
2 y
4
5215 P
0
5 (1, 2)
11. xy
3
1 3y
2
1 x
2
5 21 P
0
5 (1, 2)
12. x
2
y 1 ln(y) 5 1 P
0
5 (21, 1)
13. xe
y21
1 y
2
5 4 P
0
5 (3, 1)
14. 5x
3
x 1 2y
x 2 y
5 0 P
0
5 (1, 2)
c In Exercises 1524, use implicit differentiation to find the
tangent
line to the given curve at the given point P
0
. b
15. xy21 5
ffiffi
ffi
x
p
1
ffiffiffi
y
p
P
0
5 (4, 1)
16. x
3
2 y
3
1 4y 5 5 P
0
5 (2,2 1)
3.8 Implicit Differentiation 243

17. sin
2
(x) 1 cos
2
(y) 5 5/4 P
0
5 (π/3, π/4)
18. 7x
1/2
2 xy
1/2
5 3 P
0
5 (9, 4)
19. x 1 3/y 1 ln(y) 5 5 P
0
5 (2, 1)
20. x 1 y/x 2 exp (y
2
) 5 2 P
0
5 (3, 0)
21. e
xy
5 2y
2
2 1 P
0
5 (0, 21)
22. 2
x2y
5 xy
3
P
0
5 (2, 1)
23. ln (xy 2 1)1 y
2
5 4 P
0
5 (1, 2)
24. xe
x21
2 ln (xy) 5 1 P
0
5 (1, 1)
c In Exercises 2528, use implicit differentiation to find the
normal
line to the given curve at the given point P
0
. b
25. xy
4
2 x
3
y 5 16 P
0
5 (2, 2)
26. x
4
2 8y 1 y
6
5 9 P
0
5 (2, 1)
27. x 2 y 1 sin (2y) 5 1 P
0
5 (π/4, π/4)
28. x
2
2 3xy
2
1 1 5 1/yP
0
5 (3, 1)
c In Exercises 2934, find dy/dx and d
2
y/dx
2
at the point P
0
by implicit differentiation. b
29. y
3
1 y 1 x 5 4 P
0
5 (2, 1)
30. y
3
2 2xy 5 20 P
0
5 (23, 2)
31. xy 2 6/y 5 4 P
0
5 (2, 3)
32. y 2 sin (2y) 5 x ln( x) P
0
5 (1, 0)
33. 2e
y
5 3 2 x 1 yP
0
5 (1, 0)
34. 2x 1 y
1/3
1 y 5 0 P
0
5 (1,21)
c In Exercises 3546, find the tangent line to the parametric
curve x 5 ϕ
1
(t), y 5 ϕ
2
(t) at the point corresponding to the
given value t
0
of the parameter. b
35. ϕ
1
(t) 5 t
2
1 1, ϕ
2
(t) 5 t
3
1 1 t
0
5 1
36. ϕ
1
(t) 5 t
3
1 t, ϕ
2
(t) 5 t
2
1 1 t
0
5 1
37. ϕ
1
(t) 5 t
3
1 t, ϕ
2
(t) 5 t
3
2 tt
0
5 2/3
38. ϕ
1
(t) 5 cos (2t), ϕ
2
(t) 5 sin (3t) t
0
5 π/4
39. ϕ
1
(t) 5 t 1 cos (t), ϕ
2
(t) 5 t 1 sin (t) t
0
5 π/4
40. ϕ
1
(t) 5 t/(1 1 t
2
), ϕ
2
(t) 5 t
2
/(1 1 t
2
) t
0
5 1/2
41. ϕ
1
(t) 5 t/(1 1 t
2
), ϕ
2
(t) 5 t
3
/(1 1 t
2
) t
0
5 2/3
42. ϕ
1
(t) 5 te
t
, ϕ
2
(t) 5 t 1 e
t
t
0
5 0
43. ϕ
1
(t) 5 exp (cos (t)), ϕ
2
(t) 5 exp (sin (t)) t
0
5 π/6
44. ϕ
1
(t) 5 1/ (1 1 t
2
), ϕ
2
(t) 5 t (1 1 ln (t)) t
0
5 1
45. ϕ
1
(t) 5 2
t
1 3, ϕ
2
(t) 5 3
t
1 2 t
0
5 1
46. ϕ
1
(t) 5 log
2
(t), ϕ
2
(t) 5 t log
3
(t). t
0
5 3
Further Theory and Practice
47. Show that the tangent lines to the curve x
2
2 4xy 1 y
2
5 9
at the points where the curve crosses the x-axis are
parallel.
48. Find all points on the curve xy 2 2x
2
1 y
2
5 8 where the
tangent line has slope 22, 21, 0, 1, or 2. Show that no
tangent line to the curve is vertical.
49. The curve x
2
2 xy 1 y
2
5 4 is an ellipse. Notice that
P 5 (a, b) is on the ellipse if and only if Q 5 (2a, 2b)ison
the ellipse. Assuming that P and Q are both points on the
ellipse, show that the tangent lines at P and Q are parallel.
50. Suppose that (x
0
,y
0
) is a point on the ellipse x
2
/a
2
1
y
2
/b
2
5 1. Show that the tangent line to the ellipse at (x
0
,
y
0
) is given by
x
0
x
a
2
1
y
0
y
b
2
5 1:
51. For each positive value of α, the equation
x
3
2 3αxy 1 y
3
5 0
defines a curve known as a Folium of Descartes (see
Figure 4 of this chapter’s Genesis and Development for a
plot). Suppose that the point P 5 (a, b) is on the Folium
of Descartes. Because the equation is symmetric in x and
y, it follows that Q 5 (b, a) is also on the curve. What is
the product of the slopes of the tangent lines at P and Q?
52. Let S and T be open intervals in R. Let f : S - T be a
function that is differentiable and invertible. Show how to
derive the formula for
d
dt
f
21
that we learned in Theorem
2 of Section 3.6 by applying implicit differentiation to the
equation t 5 f (s).
53. The graph of the curve x
y
5 y
x
(x, y . 0) consists of the
ray x 5 y . 0 and a curve C. Find dy/dx at the point P on
C whose abscissa is 2. (Hint: Take the natural logarithm
of each side first.)
54. Use the method of implicit differentiation to find the
slope of the curve x
2/3
1 y
2/3
5 25 at the points (27, 64)
and at (27,264). Verify your answers by explicitly solving
for y and differentiating the explicit expression. Why
must you use two explicit formulas for y?
55. Let a be a positive constant. Let T be any tangent line to
ffiffiffi
x
p
1
ffiffiffi
y
p
5 a:
Compute the sum of the intercepts of T on the coordinate
axes. (The answer does not depend on the choice of T.)
56. Suppose that A 6¼0. The locus of
x
2=3
1 y
2=3
5 a
2=3
is called an astroid A
a
. Let T be a tangent line to the
astroid A
a
. Find a formula for the distance between the
two intercepts of T. How does this distance depend on T ?
57. Saha’s equation
1 2 y
y
2
5
A exp ðb=xÞ
x
3=2
describes the degree of ionization within stellar interiors.
In this equation, A and b are constants, y represents the
fraction of ionized atoms in the star, and x represents
stellar temperature in degrees Kelvin. Find dy/dx.
58. Let p and q be nonzero integers. Apply implicit differ-
entiation to the equation x
p
2 y
q
5 0 to obtain a proof of
the Power Rule for rational exponents:
d
dx
ðx
p=q
Þ5
p
q
x
ðp=qÞ21
:
244 Chapter 3 The Derivative
