Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

39. The region between the curves y 5 lnðxÞand y 5

x 2 1

e 2 1

40. The region in the ﬁrst quadrant between the curves

y 5 πx/2 and y 5 arcsin(x)

Further Theory and Practice

c In Exercises 41244, ﬁnd the area of the region(s) between

the two curves over the given range of x. b

41. f (x) 5 x (1 1 x

) g(x) 5 x/2, 0 # x # 1

42. f (x) 5 x cos(x

) g(x) 5 xsin(x

), 0 # x #

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

5π=2

43. f (x) 5 2sin(x) g(x) 5 sin(2x), 0 # x # π

44. f (x)=(x

2 8)/xg(x) 5 7(x 2 2), 1 # x # 4

c In Exercises 45248, calculate the area of the region

between

the pair of curves. b

45. x 5 y

1 6 x 52y

1 14

46. y 5 (x 2 3)/2 x 5 y

47. x 5 y

x 5 y

48. x 5 yx5 y

c In each of Exercises 49252, the given integral

f ðxÞdx

represents the area of the region in the xy-plane that lies

below the graph of f and above the interval [0, b] of the x-axis.

Express the area as an integral of the form

gðyÞdy. For

example, the integral

2xdx represents the area of the

triangle with vertices (0, 0), (1, 0), and (1, 2). This area can

also be represented as

ð1 2 y=2Þdy (see Figure 10). b

49.

ﬃﬃﬃ

50.

ðe

2 1Þdx

51.

arcsinðxÞdx

52.

ðx

5 2xÞdx

c In Exercises 53256, the integral

ðf

ðxÞ2 f

ðxÞÞdx

represents the area of a region in the xy-plane that is bounded

by the graphs of f

and f

. Express the area of the region as

an integral of the form

ðg

ðyÞ2 g

ðyÞÞdy: For example,

the integral

ðx 2 x

Þdx represents the area of the shaded

region in Figure 11. This area can also be represented as

ﬃﬃﬃ

2 yÞdy.(Hint: A sketch of the graphs of f

and f

over

the interval of integration is helpful. Calculating the given

integral is not helpful. You need not evaluate the integral

with respect to y that you obtain.) b

53.

ﬃﬃﬃ

2 x=2Þdx

54.

ð2

ﬃﬃﬃ

2 2x

Þdx

55.

ð3 2 jxjÞdx

56.

ðe 2 expðjxjÞÞdx

c In each of Exercises 57260, express the area of the given

region

as a sum of integrals of the form

f ðxÞdx. b

57. The

triangle with vertices (1, 0), (3, 0), (2, 1)

58. The triangle with vertices (1, 0), (3, 1), (2, 2)

59. The region enclosed by y 5 jxj and y 5 22x

60. The larger of the two pieces of the disk x

1 y

# 1 that is

formed when the disk is cut by the line y 5 x 1 1

c In Exercises 61264, express the area of the region as an

integral

of the form

gðyÞdy or as a sum of such

integrals. b

61. The

region of Exercise 57

62. The region of Exercise 58

63. The region of Exercise 59

64. The region of Exercise 60

c In each of Exercises 65270, a sum of integrals of the

form

f ðxÞdx is given. Express the sum as a single integral of

form

gðyÞdy. b

65.

ﬃﬃﬃ

dx 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 2 x

66.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 2

dx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 2

2 xÞdx

y  2x

x  1

y

1 

x 

x

m Figure 10

0.2 0.4 0.6 0.8 1.0

0.2

0.4

0.8

0.6

1.0

y  x

x  y



m Figure 11

5.7 More on the Calculation of Area 445

67.

ﬃﬃ

arcsinðxÞdx 1

ﬃﬃ

arccosðxÞdx

68.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 2 1

dx 5

ð3 2 xÞdx

69.

ð2 2 2

ﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

Þdx 1

ð2 2 2 x

Þdx

70.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 2 6

dx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

14 2 x

71. Find the area between the curves x 2 4y 5 1

and x

1 2xy 1 y

22x 1 3y =0.

72. The graphs of y 5 x 1 2/x and y 5 3 1 (x22)

intersect at

P 5 (2, 3), at one point to the left of P, and at one point to

the right of P. Find the total area of the regions that are

between the two graphs.

Calculator/Computer Exercises

c In Exercises 73279, plot the graphs as indicated. Then ﬁnd

the abscissas a and b of the two points of intersection. Find

the area bounded by the two graphs for a # x # b. b

73. y 5 x

1 x, y 5 62x

22.2 # x # 1.4

74. y 5 1 1 2x, y 5 exp(x) 20.1 # x # 1.3

75. y 5 ln(x)/x, y 5 (x21)/8 0.9 # x # 4

76. y 5 sin(x), y 5 123 sin(x)0# x # π

77. y 5 jxj, y 5 12x

21 # x # 0.7

78. y 5

ﬃﬃﬃ

, y 5 x 1 x

0 # x # 0.5

79. y 5 sec

(x), y 5 x 1 2 21 # x # 1

80. Let b denote the smallest positive solution of sin

(x) 5

cos(x

). Approximate the area between f (x) 5 cos(x

)and

g(x) 5 sin

(x) over the interv al [0, b].

5.8 Numerical Techniques of Integration

Although the Fundamental Theorem of Calculus provides a powerful rule for

evaluating Riemann integrals, many important deﬁnite integrals cannot be calcu-

lated exactly. The inability to calculate an integral exactly occurs when it is

impossible to express the antiderivative of the inte grand in terms of ﬁnitely many of

the functions that we know. Even integrands that do not appear to be especially

complicated can fall into this category. For example, the distance traveled by a

satellite in an elliptical trajectory involves an integral of the form

π=2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 k

sin

ðθÞ

dθ

where k is a positive constant less than 1. The value of this integral is required for

many applications, yet no elementary antiderivative exists. In fact, many real-world

problems involve integrands that have no elementary antiderivatives. Therefore it

is important to be able to approximate a deﬁnite integral to any speciﬁed degree of

accuracy. The right endpoint approximation that we learned in Section 5.1 will

accomplish that goal but not very efﬁciently. The three approximation techniques

that are introduced in this section are all better choices because they will match the

accuracy of the right endpoint approximation but at a substantially smaller com-

putational cost.

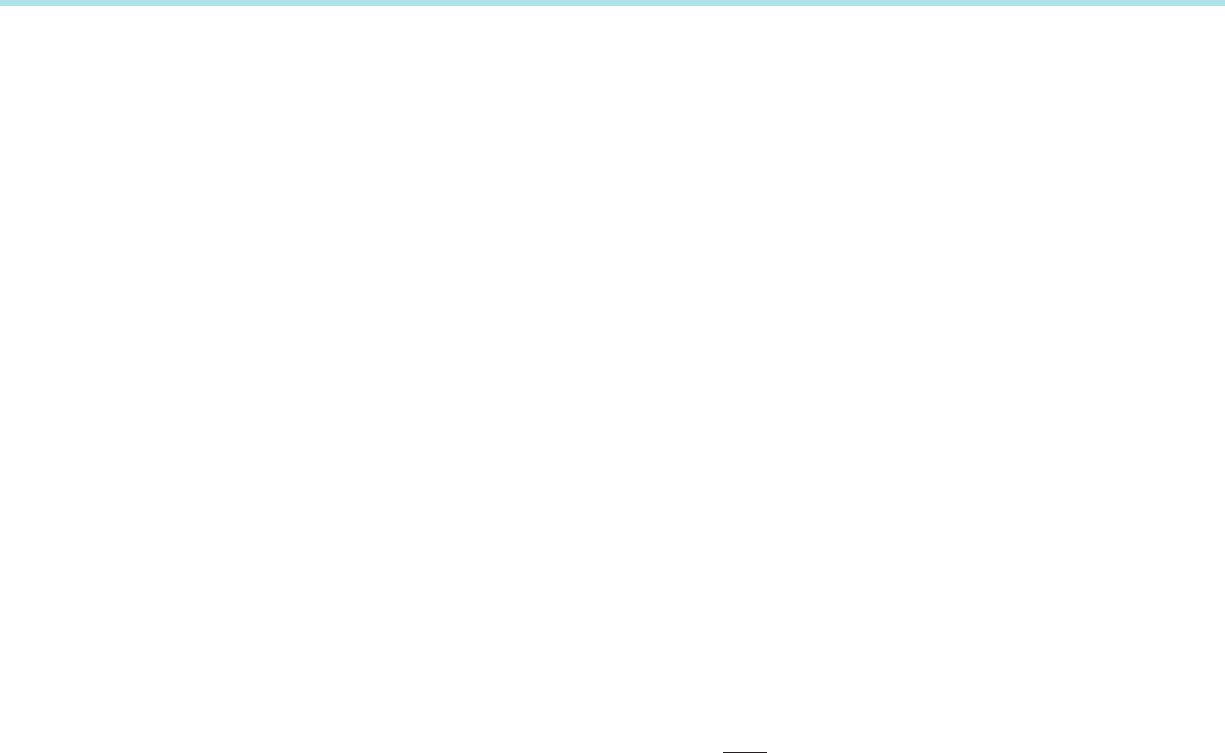
The Midpoint Rule Let f be a continuous function on the interval [a, b], and let N denote a positive

integer that is to be chosen. To approximate the integral

f ðxÞdx, we use the

uniform partition

a 5 x

, x

, , x

5 b;

which divides the interval [a, b] into N subintervals of equal length

Δx 5

b 2 a

446 Chapter 5 The Integral

Because the deﬁnite integral

f ðxÞdx is deﬁ ned as the limit lim

N-N

j5 1

f ðs

ÞΔx

of Riemann sums, it is natural to choo se the points s

2 I

5 ½x

j21

; x

 in a con-

venient manner and then use the Riemann sum

j5 1

f ðs

ÞΔx to approximate the

integral. The candidates for s

that readily come to mind are the left endpoint x

j21

of I

, the right endpoint x

of I

, and the midpoint

j21

1 x

5 a 1



j 2



Δx: ð5:8:1Þ

Because a continuous function typically either increases over an entire small

interval or decreases over the interval, the midpoint is the preferred choice (as

indicated by the shaded area of Figure 1). The resulting Riemann sum

5 Δx ðf ðx

Þ1 f ðx

Þ1 1 f ðx

ÞÞ ð5:8:2Þ

is called the midpoint approximation of order N. In general, the approximation

becomes more accurate as N increases . However, we do not want to choose N so

large that the calculation of M

becomes impractical. We may therefore state the

basic approximation problem in this way: How do we determine the smallest value

of N that allows us to be sure that M

is an acceptable approximation? The

following theorem states an error estimate that is the key to solving this problem

for the midpoint approximation.

THEOREM 1

(Midpoint Rule) Let f be a continuous function on the interval

[a, b]. Let N be a positive integer. For each integer j with 1 # j # N, let

deﬁned by equation (5.8.1). Let M

be the midpoint appro ximation

5 Δx ðf ðx

Þ1 f ðx

Þ1 1 f ðx

ÞÞ:

If C is a constant such that jf

ðxÞj# C for a # x # b, then



f ðxÞdx 2 M





ðb2 aÞ

: ð5:8:3Þ

y  f(x)

j1

m Figure 1a Left endpoint

approximation

j1

m Figure 1b Right endpoint

approximation

y  f(x)

j1

m Figure 1c Midpoint approximation

5.8 Numerical Techniques of Integration 447

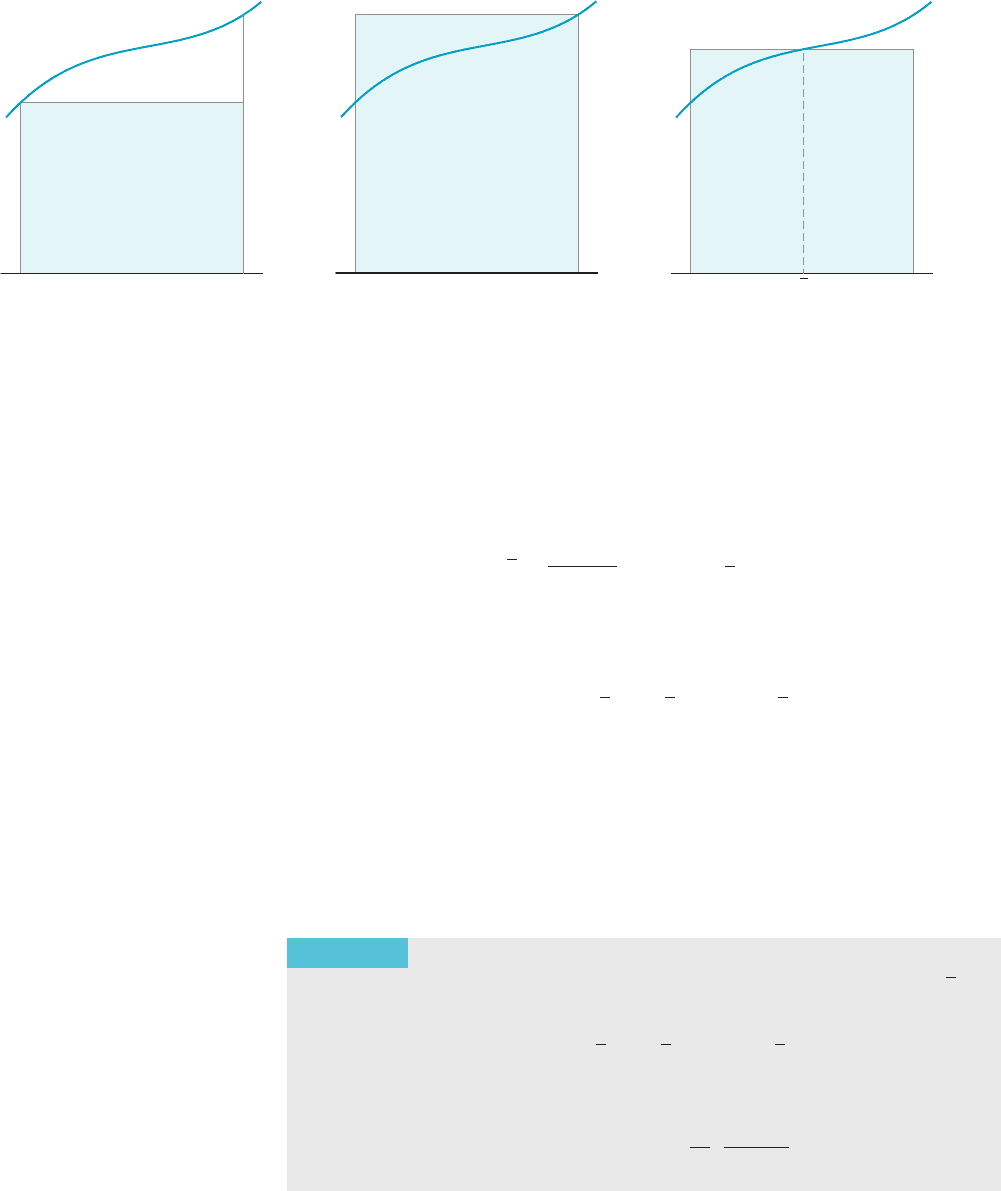
⁄ EXAMPLE 1 Let f ðxÞ5 1 = ð1 1 x

Þ. Estimate A 5

f ðxÞdx using the

Midpoint Rule with N 5 4. Based on this approximation, how small might the exact

value of A be? How large?

Solution The

points f0, 1/4, 1/2, 3/4, 1g partition the interval [0, 1] into four

subintervals of equal length (Δx 5 1/4). The midpoints of the subintervals are

1/8, 3/8, 5/8, and 7/8. The Midpoint Rule tells us that A is approximately equal to



1 1 ð1=8 Þ

1 1 ð3=8Þ

1 1 ð5=8Þ

1 1 ð7=8 Þ

 0:7867:

The number M

represents the area of the shaded rectangles in Figure 2. To ﬁnd

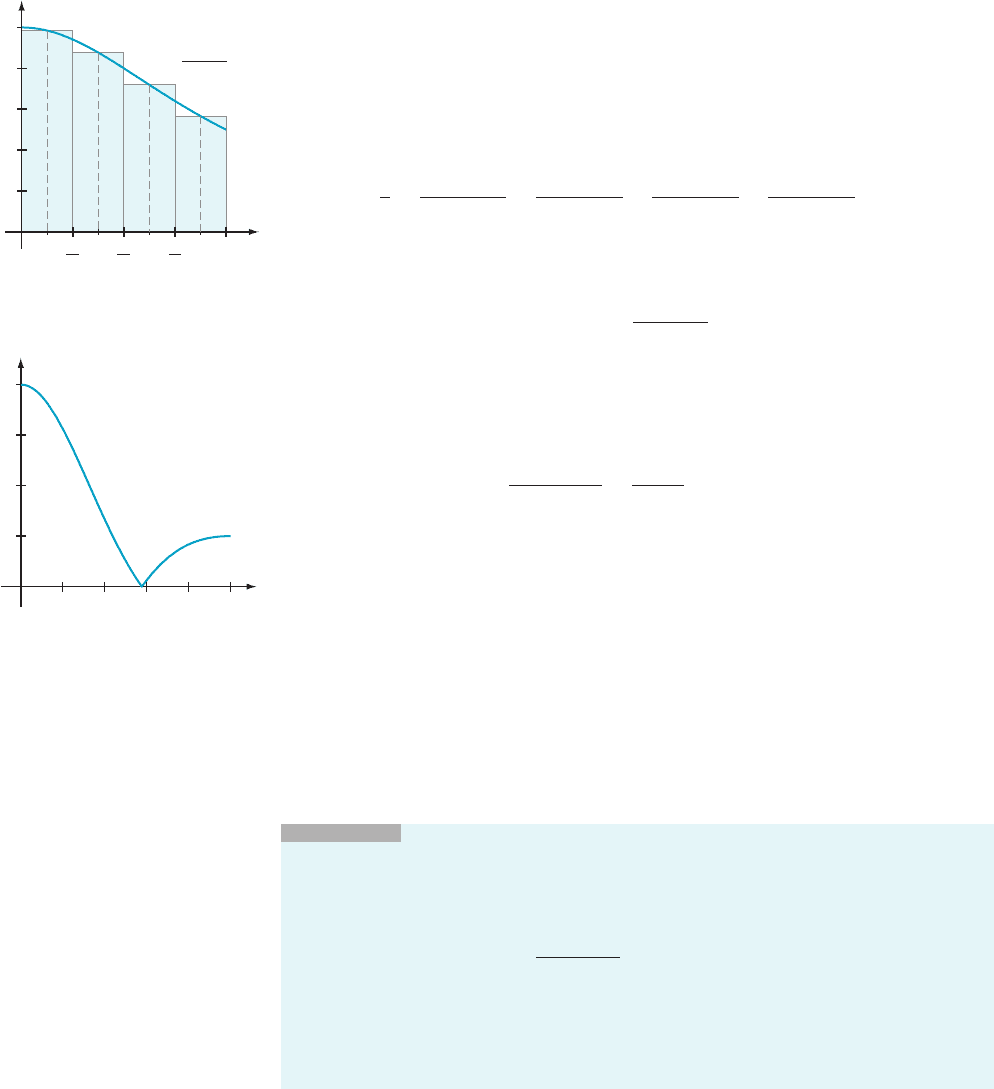
out what the exact value of A might be, we calculate that f

(x) 522x/(1 1 x

)

and

ðxÞ5

2 2

ð1 1 x

The graph of jf

j in Figure 3 reveals that the maximum value of jf

(x)j for 0 # x # 1

occurs at x 5 0 and is equal to 2. We may therefore use C 5 2ininequality(5.8.3),

which tells us that the approximation M

differs from A by no more than

C ðb 2 aÞ

24N

2  1

24  4

 0:0052:

We conclude that

0:7867

|ﬄﬄﬄ{zﬄﬄﬄ}

Midpoint approximation

2 0 :0052

|ﬄﬄﬄ{zﬄﬄﬄ}

Error estimate

# A # 0:7867

|ﬄﬄﬄ{zﬄﬄﬄ}

Midpoint approximation

1 0 :0052

|ﬄﬄﬄ{zﬄﬄﬄ}

Error estimate

: ð5:8:4Þ

By calculating the difference that begins line (5.8.4) and the sum that termi-

nates it, we see that the exact value of A may be as small as 0.7815 or as large as

0.7919. It so happens that in this example, we know that F (x ) 5 arctan(x)isan

antiderivative of the integrand f (x). Therefore the exact value of A is F (1)2F (0),

or π/4. In other words, A 5 π/4 5 0.785 . . . , which is indeed between our lower and

upper estimates. The merit of Theorem 1 is that we do not need to know the exact

value of A to be sure that it lies within the estimates.

INSIGHT

An exact value of an integral, such as A 5 π/4 in Example 1, must often be

decimalized in numerical work. By rounding an inﬁnite decimal expansion to m decimal

places, we introduce an error on the order of 5 3 10

2(m 1 1)

. According to inequality

(5.8.1), if we take N large enough so that the inequality

C ðb2 aÞ

24N

, 5 3 10

2ðm11Þ

holds, then the midpoint approximation generates an error less than 5 3 10

2(m 1 1)

.In

other words, the midpoint approximation allows us to evaluate an indeﬁnite integral with

as much precision as we would be able to obtain from the decimalization of an exact

answer.

⁄ EXAMPLE 2 Let f(x) 5 cos(x

). A plot of y 5



(x)



in the viewing window

[0.2, 1.4] 3 [0, 4] shows that



(x)



, 3.8442 for 0.2 # x # 1.4 (see Figure 4). Use a

midpoint approximation to calculate

1:4

0:2

f ðxÞdx to two decimal places.

1.0

0.8

0.6

0.4

0.2

1  x

f(x) 

m Figure 2

2.0

1.5

1.0

0.5

0.2 0.4 0.6 0.8 1.0

y   f (x)

m Figure 3 The plot of y 5

(x)j where f (x) 5 1/(1 1 x

)

448 Chapter 5 The Integral

Solution We may assign the value 3.8442 to the constant C that appears in

inequality (5.8.3). Then, with a 5 0.2 and b 5 1.4, inequality (5.8.3) becomes



1:4

0:2

cosðx

Þdx 2 M



ðb2 aÞ

3:8442

ð1:42 0:2Þ

0:2767824

To approximate

1:4

0:2

cosðx

Þdx to two decimal places, we must ﬁnd an N such that



1:4

0:2

cosðx

Þdx 2 M



# 5 3 10

To obtain this inequality, we choose N so that 0.2767824/N

# 5 3 10

,or

276.7824/5 # N

, or 7.44 . . . # N. The smallest integer satisfying this inequality is

N 5 8. On substi tuting this value of N in the inequalitie s that we have obtained, we

see that



1:4

0:2

cosðx

Þdx 2 M



0:2767824

, 5 3 10

Thus M

approximates the given integral to two decimal places. To evaluate

, we calculate Δx 5 ð 1 :4 2 0:2Þ=8 5 0:15; x

5 0:2 1

0:15 5 0:275; x

5 0:275 1

0:15 5 0:425;

5 0:425 1 0:15 5 0:575; x

5 0:575 1 0:15 5 0:725; x

5 0:725 1 0:15 5

0:875;

5 0:875 1 0:15 5 1:025; x

5 1:025 1 0:15 5 1:175, and x

5 1:175 1 0:15 5

1:325. Our approximation is

5 0:15ðcosð0:275

Þ1 cosð0:425

Þ1 cosð0:575

Þ1 1 cosð1:325

ÞÞ5 0:7522::: :

A more accurate approximation shows that

1:4

0:2

cosðx

Þdx 5 0:7498::::From this

evaluation, we see that the absolute error resulting from our approximation is

about 0.0024, which is indeed less than the speciﬁed 0.005. The importance of

inequality (5.8.3) is that it allows us to attain a speciﬁed accuracy even when the

value of the integral is not known.

The Trapezoidal Rule Suppose that f is positive over the subinterval I

5 [x

j21

, x

]. We can approximate

the area under the graph of f and over I

by the area of a trapezoid, as indicated in

0.2

0.4 0.6 0.8 1 1.2 1.4

y  3.8442

y 



cos(x

)

m Figure 4

5.8 Numerical Techniques of Integration 449

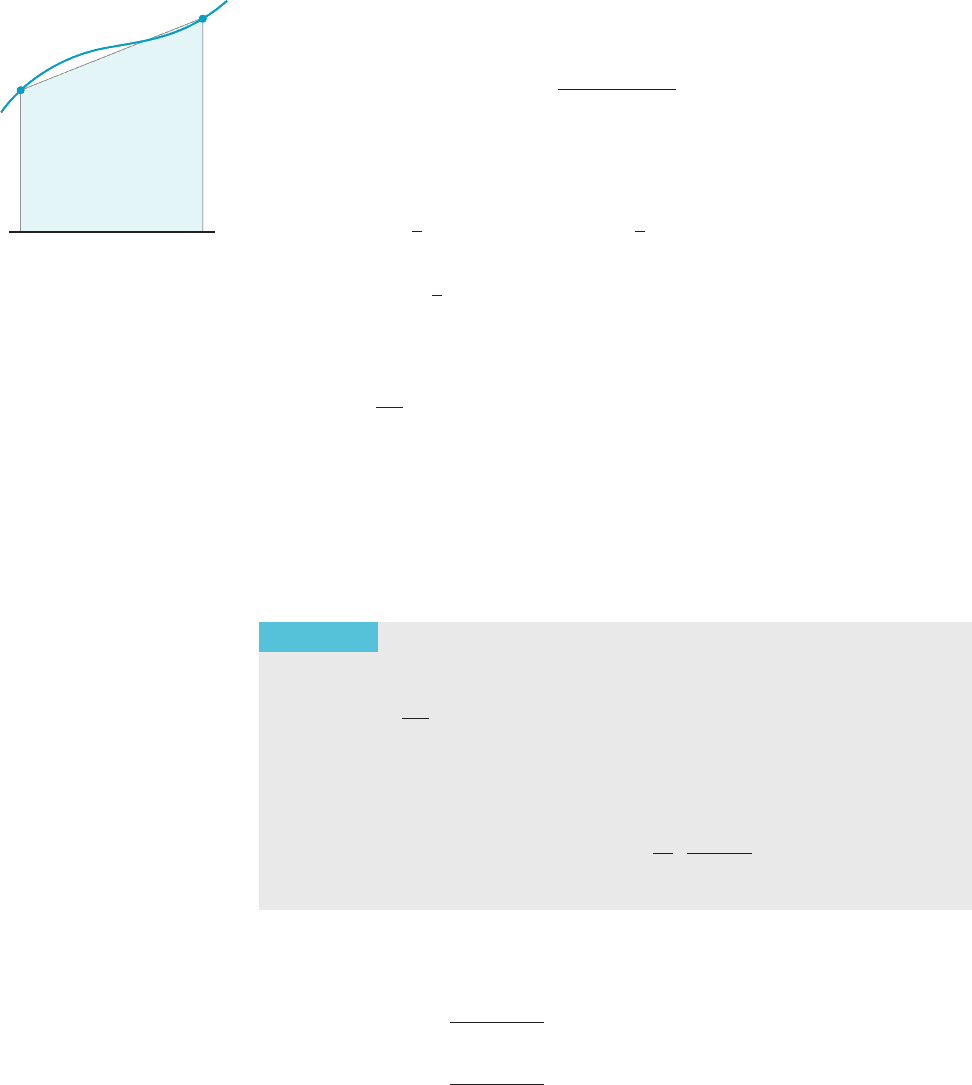
Figure 5. The trapezoidal area is the width Δx of the base times the average height

of the trapezoid:

f ðx

j21

Þ1 f ðx

 Δx:

The order N trapezoidal approximation T

is deﬁned by summing these trape-

zoidal areas:

5 A

1 A

1 1 A





f ðx

Þ1 f ðx



 Δx 1





f ðx

Þ1 f ðx



 Δx 1 





f ðx

N21

Þ1 f ðx



 Δx:

After combining terms, we obtain the formula

Δx





f ðx

Þ1 2f ðx

Þ1 1 2 f ðx

N21

Þ1 f ðx



: ð5:8: 5 Þ

It should be noted that approximation (5.8.5) is equally valid for functions that are

not positive everywhere. For example, if f (x) is negati ve on the subinterval

5 ½x

j21

; x

, then

j21

f ðxÞdx represents the negative of the area of the region that

lies under I

and above the graph of f. This negative contribution to the value of

f ðxÞdx is reﬂected by the contribution of the negative values f (x

j21

) and f (x

)to

. Similar considerations apply if f (x

j21

) and f (x

) have opposite signs.

THEOREM 2

(Trapezoidal Rule) Let f be a continuous function on the interval

[a, b]. Let N be a positive integer. Let T

be the trapezoidal approximation

Δx





f ðx

Þ1 2f ðx

Þ1 1 2 f ðx

N21

Þ1 f ðx



If jf

(x)j# C for all x in the interval [a, b], then the order N trapezoidal

approximation T

is accurate to within C ðb2aÞ

=ð12N

Þ. In other words,



f ðxÞdx 2 T





ðb2 aÞ

: ð5:8:6Þ

It is instructive to compar e the error estimates for the midpoint approximation

and the trapezoidal approximation:

C ðb2 aÞ

24N

Midpoint Rule

C ðb2 aÞ

12N

: Trapezoidal Rule

As its larger denominator suggests, the Midpoint Rule is usually more accurate

than the Trapezoidal Rule. Even so, the Trapezoidal Rule can be more suitab le for

analyzing discrete data. We illustrate this point with an example from economics.

j1

f(x

)

j1

)

m Figure 5

450 Chapter

5 The Integral

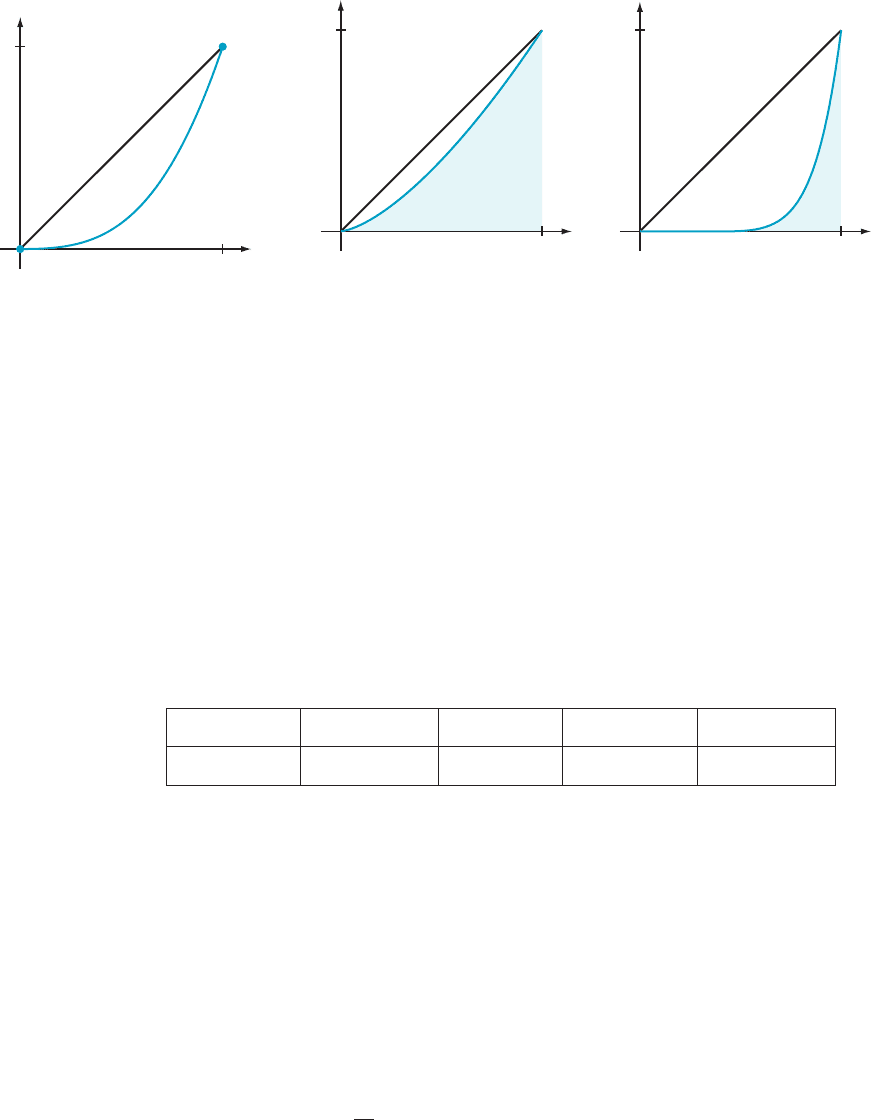
⁄ EXAMPLE 3 For each x between 0 and 100, let L (x) denote the percen-

tage of a nation’s total annual income that is earned by the lowest-earning x% of its

inhabitants during a speciﬁed year. Economists call the increasing function L:

[0, 100] - [ 0, 100] a Lorenz function. The graph of the equation y 5 L (x) is called

a Lorenz curve.NoticethatL (0) 5 0andL (100) 5 100. If all personal income were

equally distributed, then the Lorenz curve would be y 5 x.Inactuality,theLorenz

curve lies below the line y 5 x for 0 , x , 100 (see Figure 6). The area A of the region

below the Lorenz curve is used to measure the disparity of income distribution.

Notice that, because A is between 0 and 5000, the number G 5 12A/5000, known as

the Gini coefﬁcient or the coefﬁcient of inequality, is between 0 and 1. If the Lorenz

curve is y 5 x (perfectly equal income distribution), then A 5 5000 and G 5 0. As

Figure 7 shows, when income distribution becomes increasingly unequal, the Lorenz

curve approaches the bottom (y 5 0) and right side (x 5 100) of the triangle, the area

A approaches 0, and the coefﬁcient of inequality G approaches 1. Use the tabulated

data to estimate the coefﬁcient of inequality for the United States in 2006.

Lowest Fifth Second Fifth Third Fifth Fourth Fifth Highest Fifth

3.4

8.6 14.6 22.9 50.5

Percent Distribution of Total Income 2006

Solution Incom

e data is generally given by quintile (as in the table) and not in the

cumulative form needed for the Lorenz function. Nevertheless, L can be obtained

by a little bit of addition. We know that L (0) 5 0, and the table tells us that

L (20) 5 3.4. To this number, we add the percentage of income earned by the

second ﬁfth of workers: L (40) 5 3.4 1 8.6 5 12 .0. Similarly, we obtain L (60) by

adding to L (40) the percentage of income earned by the middle ﬁfth. Thus

L (60) 5 12.0 1 14.6 5 26.6. Continuing in this way, we ﬁnd L (80) 5

L (60) 1 22.9 5 26.6 1 22.9 5 49.5, and L (100) 5 L(80) 1 50.5 5 49.5 1 50.5 5 100.

Using the partition f0, 20, 40, 60, 80, 100g of [0, 100] with N 5 5 and Δx 5 20, we

obtain the following approximation from the Trapezoidal Rule:

A 5

100

LðxÞdx 

ð0 1 2  3:4 1 2  12:0 1 2  26:6 1 2  49:5 1 100Þ5 2830:0:

Therefore the coefﬁcient of inequality is approximately 122830/5000  0.434.

100

G  0.20

Area  4000

Area  1111

100

G  0.78

100

m Figure 7

(100, 100)

y  x

y  L(x)

100

Lorenz

curve

m Figure 6

5.8 Numerical Techniques of Integration 451

INSIGHT

Example 3 is typical of many discrete data problems in which the Mid-

point Rule does not permit effective use of the data. In Example 3, the midpoints of the

partitioning subintervals are

5 10; x

5 30;:::; x

5 90. Notice that the values L ð x

are not available. Yet these are the very values of L that we would need to apply the

Midpoint Rule.

Simpson’s Rule The graph of f over a small subinterval will typically be concave up or concave

down. Because the Trap ezoidal Rule and Midpoint Rule approximations are based

on straight line approximations to the graph of f, neither rule is able to reﬂect

concavity. However, if we approximate the graph of f over a small subinterval by a

parabola, as in Figure 8, then we can take into account the concavity of f. This idea

leads to the most accurate of the approximation rules that we will discuss—

Simpson’s Rule.

To derive a formula for Simpson’s Rule, we need to know the area under an arc

of a parabola. The required formula is stated in the next theorem. It is used only in

the derivation of Simpson’s Rule and need not be memorized.

THEOREM 3

If P(x) 5 Ax

1 Bx 1 C, and if I 5 [α , β] is an interval with mid-

point γ, then

PðxÞdx 5

β 2 α

ðPðαÞ1 4 PðγÞ1 Pð βÞÞ:

Proof. We

calculate

PðxÞdx 5



Aβ

Bβ

1 Cβ





Aα

Bα

1 Cα



ðβ 2 αÞð2Aα

1 3αB 1 2αAβ 1 6C 1 3βB 1 2Aβ

Þ after factoring:

It is now simply a matter of patient algebraic calculation to show that P ( α) 1

4P (γ) 1 P (β) equals the last factor. ’

To formulate Simpson’s Rule, we select a partition of [a,

b] with an even

number (N 5 2‘) of subintervals of equal length Δx. We pair up the ﬁrst and second

intervals, the third and fourth intervals, and so on. Over each pair of intervals, we

approximate f by a parabola passing through the points on the graph of f corre-

sponding to the three endpoints of the intervals. (Because the equation of a

parabola y 5 Ax

1 Bx 1 C has three coefﬁcients, a parabola is uniquely deter-

mined by any three points through which it passes.) The paired intervals are

½x

2j22

; x

2j21

 and ½x

2j21

; x

ðj 5 1;:::;‘Þ

For each j from 1 to ‘, the approximating parabola P

passes through the three

points (x

2j22

, f (x

2j22

)), (x

2j21

, f (x

2j21

)), and (x

, f (x

)) (as in Figure 9). By

y  f(x)

y  Ax

 Bx  C

aba  b

m Figure 8 Approximating the

arc of a curve with parabolic arc

2j1

, f (x

2j1

))

2j2

, f(x

2j2

))

, f(x

))

2j2

2j1

m Figure 9

452 Chapter

5 The Integral

applying Theorem 3, with α 5 x

2j22

,γ 5 x

2j21

, and β 5 x

, we see that the integral of

the parabola over the interval [x

2j22

, x

]is

2 x

2j22

ðP

ðx

2j22

Þ1 4P

ðx

2j21

Þ1 P

ðx

ÞÞ

2Δx

ðf ðx

2j22

Þ1 4f ðx

2j21

Þ1 f ðx

ÞÞ

Δx

ðf ðx

2j22

Þ1 4f ðx

2j21

Þ1 f ðx

ÞÞ:

Finally, we add the integrals from j 5 1toj 5 ‘ to obtain Simpson’s approximation

f ðxÞdx:

Δx





f ðx

Þ1 4f ðx

Þ1 2f ðx

Þ1 4f ðx

Þ1 1 2f ðx

N22

1 4f ðx

N21

Þ1 f ðx



: ð5:8:7Þ

THEOREM 4

(Simpson’s Rule). Let f be continuous on the interval [a,b]. Let N

be a positive even integer. If C is any number such that jf

(4)

(x)j# C for a # x # b,

then



f ðxÞdx 2 S



180



ðb2 aÞ

: ð5:8:8Þ

⁄ EX

AMPLE 4 Let f (x) 5 1/(1 1 x

). Estimate A 5

f ðxÞdx using Simp-

son’s Rule with N 5 4. In what interval of real numbers does A lie? (In Example 1,

we answered this question using the Midpoint Rule.)

Solution Becau

se N 5 4 is even, we can apply Simpson’s Rule. The length of each

subinterval in the order 4 uniform partition of the interval of integration, [0, 1], is

Δx 5 1/4. The points of the partition are x

5 0, x

5 1/4, x

5 1/2, x

5 3/4, and

5 1. At these points, we calculate f (x

) 5 1, f (x

) 5 1/(1 1 (1/4)

) 5 16/17,

f (x

) 5 1/(1 1 (1/2)

) 5 4/5, f (x

) 5 1/(1 1 (3/4)

) 5 16/25, and f ( x

) 5 1/2.

According to Simpson’s Rule:

1 1 x

dx  S

1=4

1 1 4 

1 2 

1 4 





8011

850

0:78539: ¥

We now estimate how accurate this approximation is. With successive appli-

cations

of the Quotient Rule, we calculate that

ð4Þ

ðxÞ5 24 

2 10x

1 1

ð11 x

Using the methods from Section 4.3 in Chapter 4, we can determine that, for x in

[0, 1], jf

(4)

(x)j attains a maximum value of 24. Plott ing jf

(4)

j also reveals this bound

(see Figure 10). Taking C 5 24 and N 5 4 in inequality (5.8.8) shows that Simpson’s

Rule with N 5 4 is accurate to within

y  24

 10x

 1

(1  x

)

m Figure 10

5.8 Numerical Techniques of Integration 453

24  1

180  4

 0:00052 :

The exact value of A is therefore between S

20.00052 5 0.78487 and S

1 0.00052 5

0.78591. In other words, A lies in the interval [0.78487, 0.78591]. As noted in Example

2, the exact value of A is π/4 5 0.78539 . . . , which is indeed between the upper and

lower bounds we determined.

INSIGHT

The error bounds of inequalities (5.8.3), (5.8.6), and (5.8.8) are worst-case

estimates. An approximation rule often yields an estimate of an integral that is much

better than the error bound suggests. For instance, the actual error in Example 4 is

π/4 2 0.78539216 5 6.0034 . . . 310

, a number that is signiﬁcantly smaller than 0.00052,

the upper bound for the error that is furnished by inequality (5.8.8).

Using Simpson’s Rule

with Discrete Data

In many practical instances, the value of a deﬁnite integral

f ðxÞdx is needed

even though a formula for f (x) is not known. Instead, the values of f are measured

at a discrete set of points. Under these circumstances, the integral must be

approximated. In Example 2, we considered a discrete data problem that arises in

economics. The following example from physiology is also typical.

The rate r at which blood is pumped from the heart is called cardiac output.

The units of cardiac output are volume/time (such as liters per minute). In the

impulse injection method of measuring cardiac output, a mass M of dye (or

radioactive isotope) is injected into a pulmonary vein. Let t 5 0 correspond to the

time of injection, and let t 5 T corres pond to the time required to pump all the dye

from the heart. The concentration c (t) of dye (in units of mass/volume) that is

pumped from the heart into the aorta is monitored. The mass of dye pumped from

the heart in the time interval [t, t 1 Δt] is approximately

cðt Þ

mass of dye

volume

 r  Δt

volume

time

|ﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ}

Volume

|ﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ}

Mass of dye:

If we partition the time interval [0, T] into N subintervals of equal length Δt, then

the Riemann sum

j5 1

cðt

j21

ÞrΔt approximates the amount of dye pumped from the

heart. Letting Δt - 0, we obtain

Mass of dye injected

r  cðtÞdt

Mass of dye pumped out:

In obtaining this formula, we have assumed that M is small enough that recircu-

lation does not occur before time T. (Blood can travel from the heart to the farthest

extremity of the circulatory system and back in as little as 12 seconds.) We solve for

r in the last equation and ﬁnd that cardiac output is given by

454 Chapter 5 The Integral