Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


As the next example demonstrates, using an integral table to its full advantage
can sometimes require considerable resourcefulness.
⁄ EX
AMPLE 8 Use a table of integrals to evaluate
Z
e
3t
1 2 e
4t
dt:
Solution Turn
ing to the table of integrals at the back of this text, we see no
suitable formula among those pertaining to integrands with the term e
x
. How ever,
if we let x 5 e
t
, then the denominator of the given integrand becomes 1 2x
4
.
Because the table contains a section for integrands involving a
4
2x
4
, the
substitution x 5 e
t
,ort 5 ln(x), dt 5 dx/x, is a lead worth pursuing. With this
substitution, we obtain
Z
e
3t
1 2 e
4t
dt 5
Z
x
3
1 2 x
4
1
x
dx 5
Z
x
2
1 2 x
4
dt:
Equation 61 of the table of integrals tells us that
Z
x
2
a
4
2 x
4
dx 5
1
4a
ln
a 1 x
a 2 x
2
1
2a
arctan
x
a
1 C:
With a 5 1 , this equation becomes
Z
x
2
1 2 x
4
dx 5
1
4
ln
1 1 x
1 2 x
2
1
2
arctan ðxÞ1 C:
By resubstituting x 5 e
t
, we obtain
Z
e
3t
1 2 e
4t
dt 5
1
4
ln
1 1 e
t
1 2 e
t
2
1
2
arctan ðe
t
Þ1 C: ¥
INSIGHT
Tables of integrals have remained useful even after the emergence of
powerful computer algebra systems. One reason is that computers evaluate integrals in a
way that differs qualitatively from the human approach. Computer algebra systems must
use algorithms that are designed to handle a wide array of integrands. These general
procedures may not be optimized for the particular integrand at hand. Thus Maple
correctly computes the evaluation
Z
secðxÞtan
3
ðxÞdx 5
1
3
sin
4
ðxÞ
cos
3
ðxÞ
2
1
3
sin
4
ðxÞ
cosðxÞ
2
1
3
sin
2
ðxÞcos ð xÞ2
2
3
cosðxÞ:
However, formula 193 of our table,
Z
secðxÞtan
3
ðxÞdx 5
1
3
sec
3
ðxÞ2 secðxÞ1 C;
is certainly preferable. Of course, we do not have to limit ourselves to only one of these
integration aids. Computer algebra systems have proved to be valuable in detecting
unsuspected errors in tables of integrals. And that is a good reminder—whichever of
these tools you use, your last step should be the same as if you calculated the integral by
hand: Verify the answer by differentiation.
5.6 Integration by Substitution 435

Integrating
Trigonometric
Functions
Although we know how to differentiate each trigonometric function, we have up until
now only learned to integrate the sine and cosine functions. Using the method of
substitution, we can obtain antiderivatives for the remaining trigonometric functions.
⁄ EX
AMPLE 9 Show that
Z
tanðxÞdx 5 lnðjsecðxÞjÞ1 C: ð5:6:5Þ
Solution When
we are presented with an integrand that is made up of
trigonometric functions, it is sometimes helpful to rewrite the expression entirely
in terms of sines and cosines. In this case, we have
Z
tanðxÞdx 5
Z
sinðxÞ
cosðxÞ
dx:
Now the substitution u 5 cos(x), du 52sin(x) dx converts the last integral to
Z
2
1
u
du 52lnðjujÞ1 C:
Resubstituting u 5 cos(x) yields the solution:
R
tanðxÞdx 52lnðjcosðxÞjÞ1 C
5 lnðjcosðxÞj
21
Þ1 C
5 lnðjsecðxÞjÞ1 C: ¥
INSIGHT
Remember that, as a rule of thumb, the tangent and secant functions
occur together in differentiation and integration formulas. For example, we have already
learned that
Z
sec
2
ðxÞdx 5 tanðxÞ1 C and
Z
secðxÞtanðxÞdx 5 sec ðxÞ1 C:
Equation (5.6.5) is another instance in which tan(x) and sec(x) appear together in an
integral formula.
The formula for the an tiderivative of the secant, which we derive in the next
example, is more complicated.
⁄ EX
AMPLE 10 Use a substitution to derive the formula
Z
secðx Þdx 5 lnðjsecðxÞ1 tanðxÞjÞ1 C: ð5:6:6Þ
Solution By
examining the right side of formula (5.6.6) and deducing that it arises
as the antiderivative of
R
ð1=uÞdu where u 5 sec(x) 1 tan(x), we can spot the way to
proceed, which otherwise would be far from obvious. We need sec(x) 1 tan(x)in
the denominator, so the trick is to multiply and divide the integrand by this
expression:
Z
secðxÞdx 5
Z
secðxÞ
secðxÞ1 tanðxÞ
secðxÞ1 tanðxÞ
dx 5
Z
secðxÞtanðxÞ1 sec
2
ðxÞ
secðxÞ1 tanðxÞ
dx:
436 Chapter 5 The Integral

Now we make the substitution u 5 sec(x) 1 tan(x), du 5 (sec(x)tan(x) 1 sec
2
(x)) dx.
The last integral becomes
R
ð1=uÞdu 5 lnðjujÞ1 C. When we resubstitute u 5
sec(x) 1 tan(x), we obtain formula (5.6.6). A detailed historical discussion of this
formula may be found in Genesis and Development 6.
¥
The antiderivative formulas for the cotangent and cosecant may be derived by
following the methods for the tangent and secant, respectively. They are included
in the table that follows.
Summary of Integ ration Rules
R
tanðxÞdx 5 lnðjsecðxÞjÞ1 C
R
cotðxÞdx 52lnðjcscðxÞjÞ1 C
R
secðxÞdx 5 lnðjsecðxÞ1 tanðxÞjÞ1 C
R
cscðxÞdx 52lnðjcscðxÞ1 cotðxÞjÞ1 C
QUICK QUIZ
1. The method of substitution is the antiderivative form of what differentiation
rule?
2. Evaluate
R
cos
3
ðxÞsinðxÞdx.
3. Evaluate
R
5
3
x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
x
2
2 9
p
dx.
4. Evaluate
R
π=4
0
tanðxÞdx.
Answers
1. Chain Rule 2. 2cos
4
(x)/4 3. 64/3 4. ln(2)/2
EXERCISES
Problems for Practice
c In Exercises 1210, determine a substitution that will
simplify the integral. In each problem, record your choice of u
and the resulting expression for du. Then evaluate the
integral. b
1.
R
sinð3xÞdx
2.
R
24
sec
2
ð4tÞdt
3.
R
64ðx
8
11Þ
25
x
7
dx
4.
R
24 t
ffiffiffiffiffiffiffiffiffiffiffiffi
t
2
1 4
p
dt
5.
R
30 x
2
ðx
3
25Þ
3=2
dx
6.
R
ð
ffiffi
t
p
1 4Þ
6
t
21=2
dt
7.
R
sinðsÞcos
4
ðsÞds
8.
Z
24
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffiffi
t
p
þ 1
p
ffiffi
t
p
dt
9.
Z
sinðπ=tÞ
t
2
dt
10.
R
24 t
2
secðt
3
Þtanðt
3
Þdt
c Use the method of substitution to calculate the indefinite
integrals
in Exercises 11222. b
11.
R
16 x ðx
2
1 1Þ
7
dx
12.
R
24 x
2
ð5 2 4x
3
Þ
22
dx
13.
Z
x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 x
2
p
dx
14.
R
24 cosð3xÞsinð3xÞdx
15.
Z
sinðxÞ
cos
2
ðxÞ
dx
16.
Z
lnðxÞ
x
dx
17.
R
24 sin
5
ð2xÞcosð2xÞdx
18.
R
24 x cosð4x
2
2 5Þdx
19.
Z
24x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 x
2
p
dx
20.
Z
24 sinðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 1 cosðxÞ
p
dx
5.6 Integration by Substitution 437

21.
Z
sinð
ffiffiffi
x
p
Þ
ffiffiffi
x
p
dx
22.
Z
sinðtÞ2 cosðtÞ
ðsinðtÞ 1cos ð tÞÞ
2
dt
c Use the method of substitution to evaluate the definite
integrals
in Exercises 23236. b
23.
R
2
1
ðt
2
2 tÞ
5
ð2t 2 1Þdt
24.
R
5
0
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 3x
p
dx
25.
Z
4
0
x
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
x
2
1 1
r
dx
26.
R
π
π=3
cos
3
ð5xÞsinð5xÞdx
27.
Z
ffiffiffiffiffiffiffi
3π=8
p
ffiffiffiffiffiffi
π=4
p
24x cosð4x
2
2 πÞdx
28.
Z
3
0
sinðπ
ffiffiffiffiffiffiffiffiffiffiffi
t 1 1
p
Þ
ffiffiffiffiffiffiffiffiffiffiffi
t 1 1
p
dt
29.
Z
0
21
24
x
2
ðx
3
2 1Þ
5
dx
30.
Z
1
0
24
expðxÞ
ð1 1 expðxÞÞ
2
dx
31.
Z
π
2
π
2
=4
cosð
ffiffiffi
x
p
Þ
ffiffiffi
x
p
dx
32.
R
2
0
ð8x 1 5Þð4x
2
1 5x 1 1Þ
22=3
dx
33.
R
π=3
0
sec
3
ðθÞtanðθÞdθ
34.
R
9
4
t
23=2
sinðπ=
ffiffi
t
p
Þdt
35.
Z
π=4
0
24 tanðxÞ sec
2
ðxÞ
ð1 1 2 tanðxÞÞ
2
dx
36.
Z
e
1
ffiffiffiffiffiffiffiffiffiffiffi
lnðxÞ
p
x
dx
c Evaluate the definite integrals in Exercises 37244. b
37.
R
π=8
0
tanð2xÞdx
38.
R
π
π=2
cotðx=2Þdx
39.
R
π
0
secðx=4Þdx
40.
R
π
π=2
cscðx=3Þdx
41.
R
1=2
0
xtanðπ x
2
Þdx
42.
R
4
2
24 cotðπ=xÞ=x
2
dx
43.
R
π=2
0
cosðxÞsec
π sinðxÞ=4
dx
44.
Z
2
1
24
x
2
csc
π
3
2x 2 1
x
dx
c In Exercises 45252, use the indicated formula from the
table
of integrals at the back of the text to evaluate the given
integral. b
45.
Z
1
ð4t 1 3Þðt 1 3Þ
dt ðFormula 23Þ
46.
Z
3t 1 2
2t 1 1
dt ðFormula 22Þ
47.
Z
9 1 6t 1 t
2
25 1 6t 1 t
2
dt ðFormula 35Þ
48.
Z
t
1 2 16t
4
dt ðFormula 60Þ
49.
Z
1
4 1 expð2t Þ
dt ðFormula 39Þ
50.
Z
1
ð1 1 4t
2
Þ
2
dt ðFormula 32Þ
51.
Z
1
2 1
ffiffi
t
p
dt ðFormula 7Þ
52.
Z
cotðtÞ
3 1 2 sinðtÞ
dt ðFormula 19Þ
Further Theory and Practice
c Calculate the integrals in Exercises 53276. b
53.
R
x ð2x 1 3Þ
1=2
dx
54.
Z
x
2
ðx 2 1Þ
3
dx
55.
Z
x
ffiffiffiffiffiffiffiffiffiffiffiffi
x 1 3
p
dx
56.
R
x
3
ðx
2
2 1Þ
1=2
dx
57.
R
x
5
ð6 1 x
2
Þ
21=2
dx
58.
R
x
2
ðx 1 2Þ
1=3
dx
59.
R
ðx 1 2Þ
ffiffiffiffiffiffiffiffiffiffiffi
x 2 5
p
dx
60.
Z
24 x
3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 x
2
p
dx
61.
Z
cosðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 sin
2
ðxÞ
q
dx
62.
Z
π=3
0
sinðxÞ
1 2 sin
2
ðxÞ
dx
63.
Z
lnðx
11
Þ2 lnðx
7
Þ
x
dx
64.
Z
lnðxÞ
x
2
1
x lnðxÞ
dx
65.
Z
2
x lnðx
2
Þ
2
2
x ln
2
ðxÞ
dx
66.
Z
x
x
2
1 1
1 2
1
x
2
dx
67.
Z
arctanðxÞ
1 1 x
2
dx
68.
Z
expðxÞ
1 1 expðxÞ
dx
69.
Z
expð xÞ
1 1 expð2xÞ
dx
70.
Z
expð 2xÞ
1 1 expðxÞ
dx
438 Chapter 5 The Integral
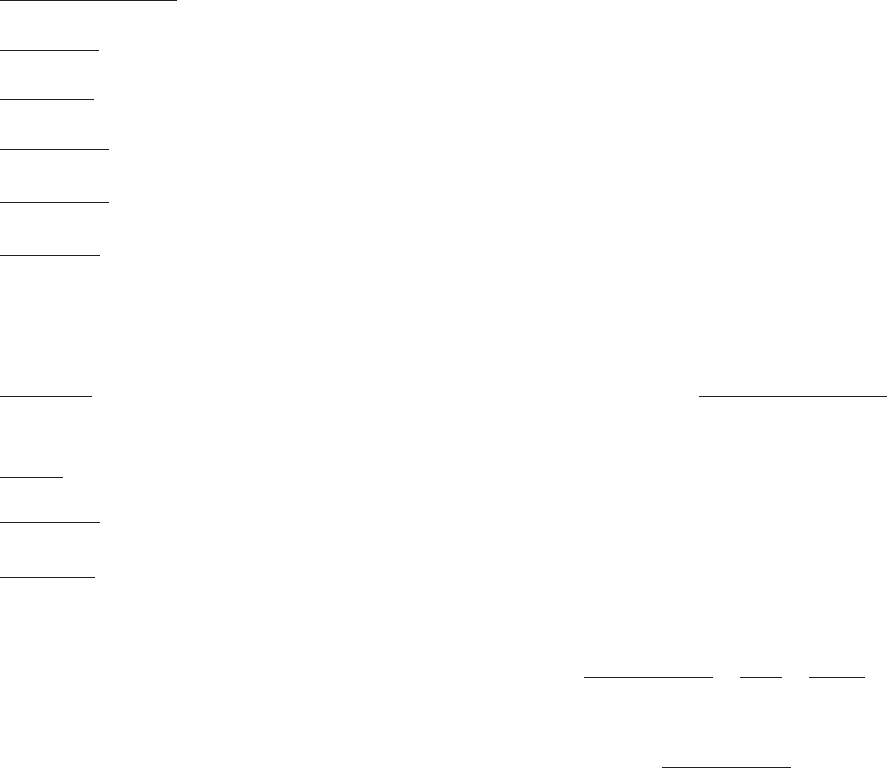
71.
Z
expðxÞ
1 1 2 expðxÞ1 expð2xÞ
dx
72.
Z
x 1 arcsinðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
dx
73.
Z
6x
3
1 3x 1 1
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
dx
74.
Z
expðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 expð2xÞ
p
dx
75.
Z
expð2xÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 expð2xÞ
p
dx
76.
Z
24 expð2xÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 expðxÞ
p
dx
c In each of Exercises 77282, evaluate the given integral by
applying
a substitution to a formula from a table of
integrals. b
77.
Z
tanðtÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 1 cosðtÞ
p
dt
78.
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1
ffiffi
t
p
p
dt
79.
Z
12
t
ffiffiffiffiffiffiffiffiffiffiffiffi
1 1 t
4
p
dt
80.
Z
1
2 1 expðtÞ
2
dt
81.
Z
sec
3
ðtÞtanðtÞ
1 1 sec
2
ðtÞ
dt
82.
R
cosðlnðt ÞÞdt
83. Evaluate the integral
R
1
21
3t
2
dt directly. Calculate it again
by performing the integration separately on the two
subintervals [21, 0] and [0, 1] and making the substitution
u 5 t
2
on each.
84. Let f :[2a, a] - R be continuous and odd ( f (2x) 5
2f (x)). Show that
Z
a
2a
f ðxÞdx 5 0:
85. Let f :[2a, a] - R be continuous and even ( f (2x) 5
f (x)). Show that
Z
a
2a
f ðxÞdx 5 2
Z
a
0
f ðxÞdx:
86. Let f :[21, 1]-R be continuous. Evaluate
Z
π=2
2π=2
x f ðcosðxÞÞdx:
(See Exercise 84.)
87. Suppose that f is continuous on [a, b]. Use a substitution
to show that
Z
b
a
f ðxÞdx 5
Z
b2a
0
f ðb 2 xÞdx:
88. Suppose that f is continuous on [a, b]. Use a substitution
to show that
Z
b
a
f ðxÞdx 5
Z
b
a
f ða 1 b 2 xÞdx:
89. Suppose that f is continuous on [a, b]. Use a substitution
to show that
Z
b
a
f ðxÞdx 5 ðb 2 aÞ
Z
1
0
f ða 1 ðb 2 aÞxÞdx:
90. Suppose that f is continuous on [a, b]. let δ 5 ðb 2 aÞ=2
and μ 5 ða 1 bÞ=2. Use a substitution to show that
Z
b
a
f ðuÞdu 5 δ
Z
1
21
f ðδx 1 μÞ dx
91. Suppose that α and β are different constants. Use the
identity
sinðAÞcosð BÞ5
sinðA 1 BÞ1 sinðA 2 BÞ
2
to evaluate
R
sinðαxÞcosð βxÞdx:
92. Evaluate
Z
sec
2
ðxÞtanðxÞdx
by using the change of variable u 5 tan(x). Then evaluate
the integral by making the change of variable v 5 sec(x).
Verify that the two answers that you obtain are
equivalent.
93. Verify that
2t
3
1 5t
2
1 2t 1 1
ðt
2
1 1Þðt 1 1Þ
2
5
2t
t
2
1 1
1
1
ðt 1 1Þ
2
:
Use this decomposition to evaluate
Z
2t
3
1 5t
2
1 2t 1 1
ðt
2
1 1Þðt 1 1Þ
2
dt:
(This example shows how beneficial Theorem 1a from
Section 5.3 can be.)
94. Evaluate
R
1
0
x
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
p
dx. Start with the substitution
u 5
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
, and finish with a second substitution.
Calculator/Computer Exercises
c In Exercises 95298, determine the value of the upper limit
of integration b for which a substitution converts the integral
on the left to the integral on the right. b
95.
R
b
0
ð3t
2
þ 1Þsec
2
ðt
3
þ tÞtan
2
ðt
3
þ tÞdt 5
R
1
0
u
2
du
96.
R
b
0
ð4x
3
1 2xÞ sinðx
4
1 x
2
Þdx 5
R
π
0
sinðuÞdu
97.
R
b
0
ð1 1 e
x
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 e
x
p
dx 5
R
9
1
ffiffiffi
u
p
du
98.
R
b
1
ðx 1 1Þexpð1=x 2 lnðxÞÞ=x
2
dx 5
R
1
1=4
expðuÞdu
5.6 Integration by Substitution 439
5.7 More on the Calculation of Area
If a function f is continuous and nonnegative on an interval [a, b], then
R
b
a
f ðxÞdx $ 0.
This is clear because each of the summands in the Riemann
P
N
j5 0
f ðs
j
ÞΔx is non-
negative (because f is nonnegative). Similarly, if f is continuous and f # 0onan
interval [c, d], then
R
d
c
f ðxÞdx # 0. Again, this is justified by the fact that each sum-
mand in the Riemann Sum
P
N
j5 0
f ðs
j
ÞΔx is nonpositive (because f is nonpositive).
In the first case, the integral represents area (as discussed in Section 5.1). The same
ideas show that when f # 0, the integral represents the negative oftheareabecausethe
summands f (s
j
)Δx are negatives of the areas of the correspondin g rectangles.
We obtain from these remarks the following guidelines for determining area.
Rules for Calculating Area
1. If f (x) $ 0 for x in [a, b], then
R
b
a
f ðxÞdx equals the area of the region that is below the graph of f, above the
x-axis, and between x 5 a and x 5 b.
2. If f (x) # 0 for x in [a, b], then
R
b
a
f ðxÞdx equals the negative of the area of the region that is above the graph
of f, below the x-axis, and between x 5 a and x 5 b.
We may use these observations to solve some fairly sophisticated area
problems.
⁄ EX
AMPLE 1 What is the area of the region bounded by the graph of
f (x) 5 sin(x) and the x-axis between the limits x 5 π/3 and x 5 3π/2?
Solution Look
at Figure 1. Notice that f (x) $ 0 for x ε [π/3, π] and f (x) # 0 for x ε
[π,3π/2]. Thus the (positive) area of the region lying above [π/3, π]is
Z
π
π=3
sinðxÞdx 52cosðxÞj
π
π=3
52ð21Þ2
2
1
2
5
3
2
:
On the other hand, the (positive) area of the region lying below [π,3π/2] is
2
Z
3π=2
π
sinðxÞdx 52ð2cos ðxÞÞj
3π=2
π
5 0 2 ð21Þ5 1:
The total area is the sum of the two component areas, or 3/2 1 1, or 5/2.
¥
Theorem 1e from Section 5.3 suggests a way in which we can calculate a reas
(and integrals) for piecewise-defined functions.
⁄ EX
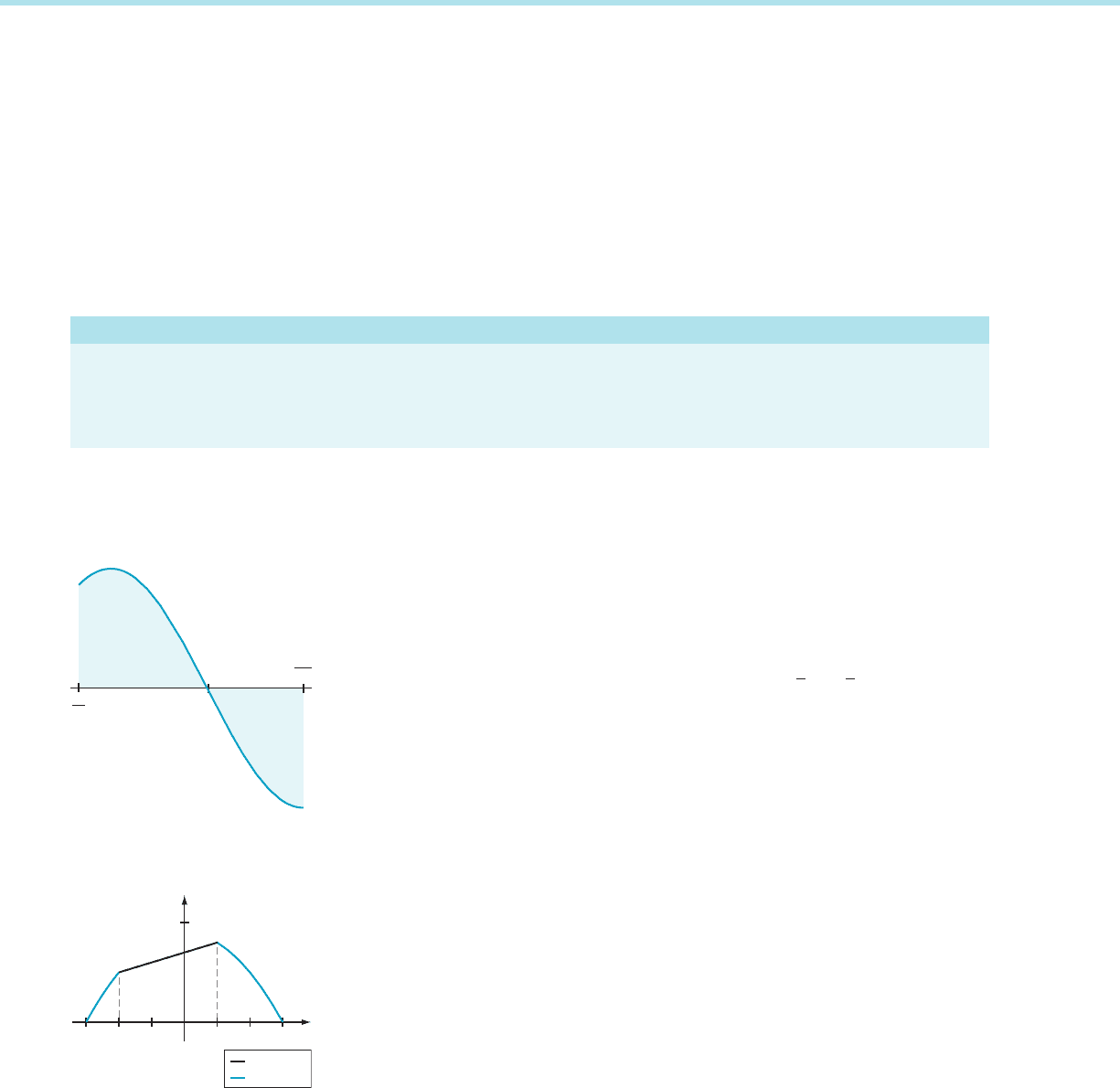
AMPLE 2 Define
f ðxÞ5
x 1 7i
f2 2 # x # 1
9 2 x
2
if x ,22orx . 1 :
What is the area of the region below the graph of f and above the x-axis?
Solution From
the definition of f, we see that f $ 0 for 23 # x # 3. (The graph of f
over this interval appears in Figure 2.) We see that the problem naturally divides
into three pieces:
y sin(x)
3
p
2
p
3
p
m Figure 1
y
x
12312
10
3
y x 7
y 9 x
2
m Figure 2
440 Chapter
5 The Integral
1. The component of area above the interval [23, 22]
2. The component of area above the interval [22, 1]
3. The component of area above the interval [1, 3]
We thus do three separate calculations.
1. When x is in [23, 22), we have f (x) 5 92x
2
and
Z
22
23
f ðxÞdx 5 9x 2
x
3
3
x522
x523
5218 1
8
3
2227 1
27
3
5
8
3
:
2. When x is in [22, 1], we have f (x) 5 x 1 7 and
Z
1
22
f ðxÞdx 5
1
2
x
2
1 7x
x5 1
x522
5
1
2
1 7
2
4
2
2 14
5
39
2
:
3. When x is in (1, 3], we have f (x) 5 92x
2
and
Z
3
1
fxðÞdx 5 9x 2
x
3
3
x5 3
x5 1
5 27 2
27
3
2 9 2
1
3
5
28
3
:
Thus the total area between the graph of f and the x-axis is 8/3 1 39/2 1 28/3,
or 63/2.
¥
The Area between
Tw o Curves
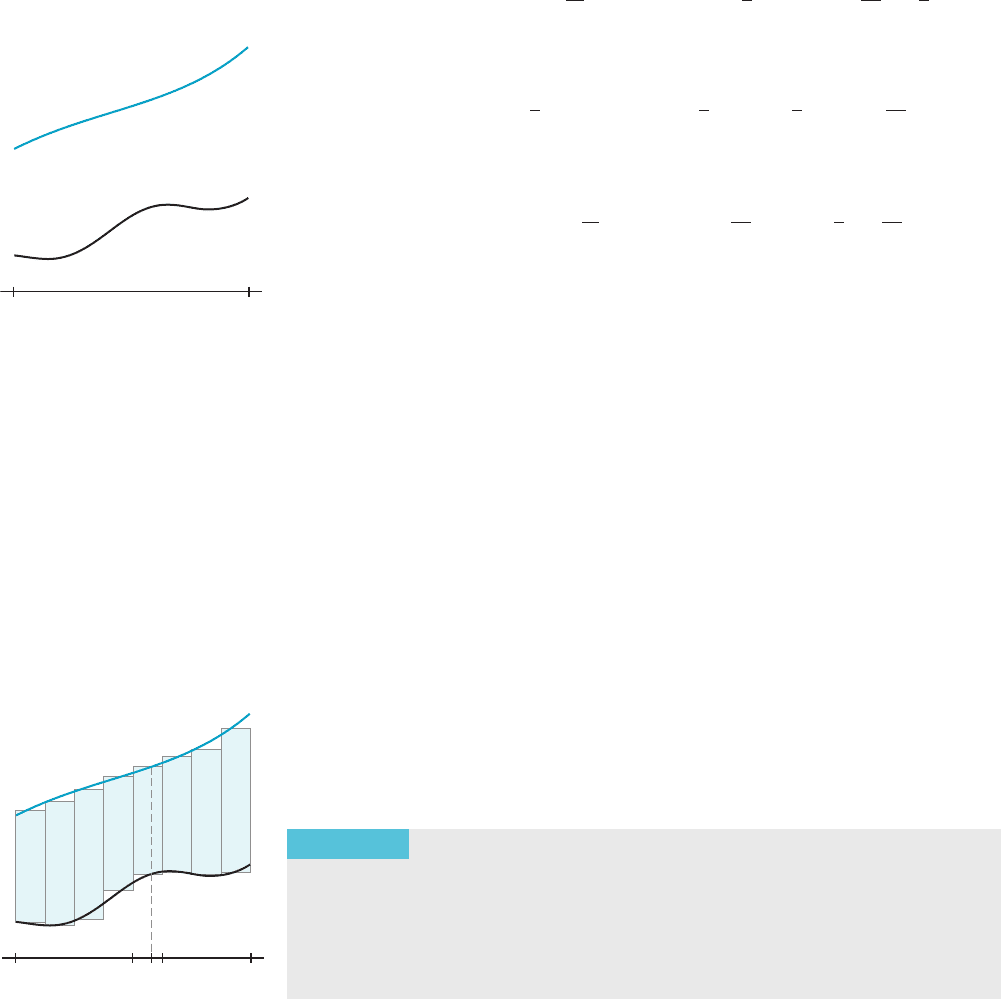
Examples 1 and 2 are special cases of the general problem of finding the area
between two curves. Suppose f and g are continuous functions with domains that
each contain the interval [a, b]. Suppose further that f (x) $ g (x) on this interval
(see Figure 3). To estimate the area below the graph of f and above the graph of g
on this interval, we let P 5 fx
0
,...,x
N
g be a uniform partition of [a, b ]. W e select
points s
j
2 I
j
5 ½x
j21
; x
j
and erect rectangles with base I
j
and height f (s
j
)2g (s
j
), as in
Figure 4. The area we wish to estimate is approximately given by the sum of the
areas of these rectangles, or
X
N
j5 1
f ðs
j
Þ2 gðs
j
Þ
Δx:
As Δx tends to 0, we expect that this sum will become a more accurate approx-
imation to the desired area. However, the sum also happens to be a Riemann sum
for the integral
Z
b
a
f ðxÞ2 gð x Þ
dx:
We have therefore derived the following result, stated as a theorem.
THEOREM 1
Let f and g be continuous functions on the interval [a, b] and
suppose that f (x) $ g (x) for all x in [a, b]. The area of the region under the
graph of f and above the graph of g on the interval [a, b] is given by
Z
b
a
f ðxÞ2 gðxÞ
dx:
f
g
a x
0
x
j1
b x
N
s
j
x
j
m Figure 4
y f (x)
y g(x)
ab
m Figure 3
5.7 More on the Calculation of Area 441
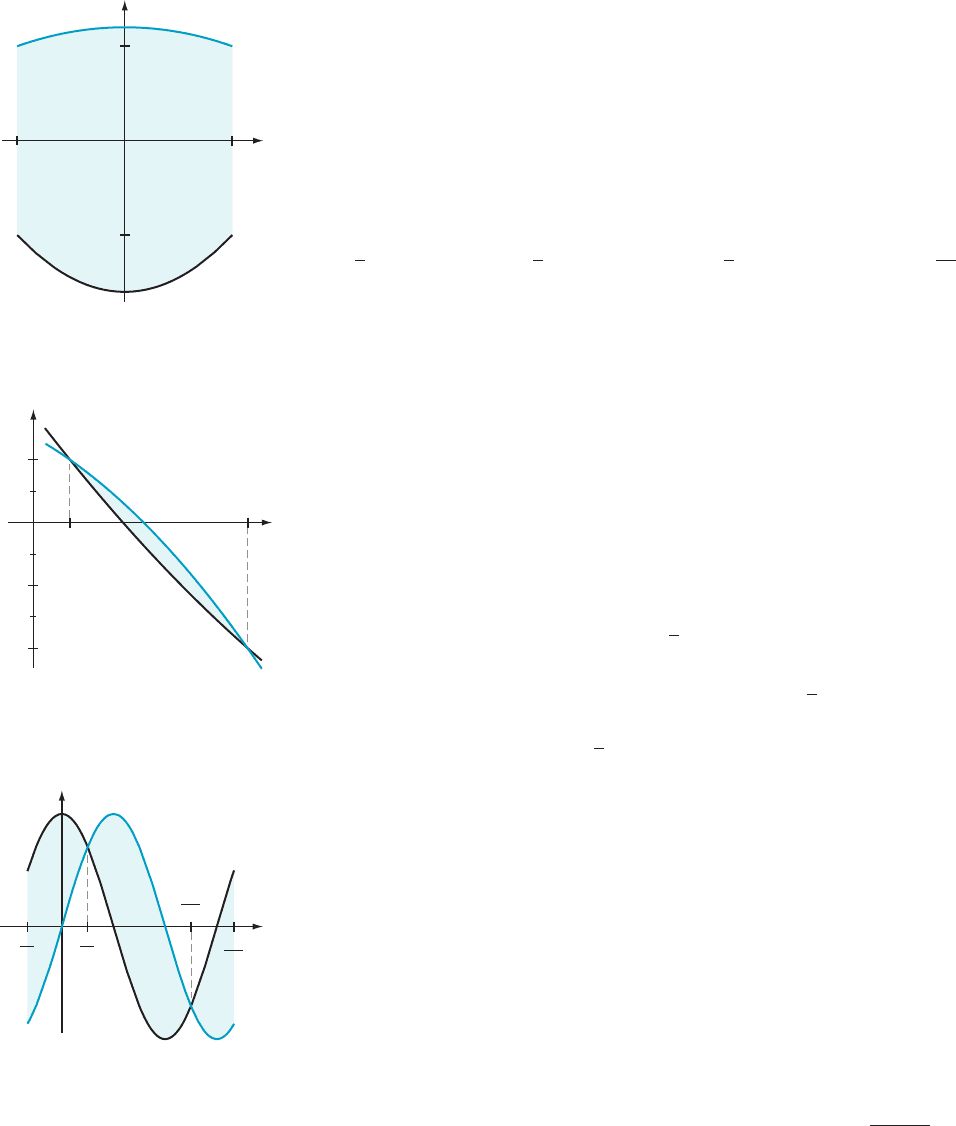
⁄ EXAMPLE 3 Calculate the area A of the region between the curves
f (x) 52 x
2
1 6 and g (x) 5 3x
2
28 for x in the interval [21, 1].
Solution We
see from the sketch in Figure 5 that f (x) $ g(x) on this interval.
According to Theorem 1, the desired area is given by
Z
1
21
ðf ðxÞ2 gðxÞÞdx 5
Z
1
21
ð2x
2
1 6Þ2 ð3x
2
2 8Þ
dx 5
Z
1
21
ð24x
2
1 14Þdx:
Therefore
A 5
2
4
3
x
3
1 14x
1
21
5
2
4
3
1 1 14 1
2
2
4
3
ð21Þ1 14 ð21Þ
5
76
3
: ¥
⁄ EX
AMPLE 4 Calculate the area between the parabolas f (x) 522x
2
1 4
and g(x) 5 x
2
29x 1 10.
Solution The
region is shaded in Figure 6. We have not specified an interval on
which to work, but we can calculate the interval of integration: The parabolas
intersect when 22x
2
1 4 5 x
2
29x 1 10, or x
2
23x 1 2 5 0. The roots are x 5 1 and
x 5 2, as can be seen either by factoring or by using the Quadratic Formula. On the
interval [1, 2], f (x) $ g (x). Thus the desired area is given by
Z
2
1
f ðxÞ2 gðxÞ
dx 5
Z
2
1
ð2 2x
2
1 4Þ2 ðx
2
2 9x 1 10Þ
dx
5
Z
2
1
ð23x
2
1 9x 2 6Þdx
5
2 x
3
1
9
2
x
2
2 6x
x5 2
x5 1
5 ð28 1 18 2 12Þ2
21 1
9
2
2 6
5
1
2
: ¥
⁄ EX
AMPLE 5 Calculate the area between the curves f (x) 5 sin(x)
and
g(x) 5 cos(x) on the interval [2π/3, 5π/3].
Solution The
graphs of f and g appear in Figure 7. Notice that f (x) $ g (x) at some
points while g(x) $ f (x) at other points. We need to break up the interval [2π/3,
5π/3] into subintervals on which either one or the other of these inequalities
is true, but not both. Thus we need to find the points of intersection of the graphs of
f and g. Setting sin(x) 5 cos(x), we see that the graphs intersect at the points x 5 π/4
and x 5 5π/4 in the interval [2π/3, 5π/3]. We therefore make separate calculations
of the area on [2π/3, π/4], the area on [π/4, 5π/4], and the area on [5π/4, 5π/3]. On
[2π/3, π/4], we have cos(x) $ sin(x) (as we can see from Figure 7), so the
corresponding area is
Z
π=4
2π=3
cosðxÞ2 sinðxÞ
dx ¼
sinðxÞþcosðxÞ
π=4
2π=3
5
ffiffiffi
2
p
1
ffiffiffi
3
p
2 1
2
:
On [π/4, 5π/4], we see that sin(x) $ cos(x), and the corresponding area is
y
f (x) x
2
6
g(x) 3x
2
8
x
5
1
5
1
m Figure 5
f (x) 2x
2
4
g(x) x
2
9x 10
x
y
21
2
2
4
m Figure 6
x
y
5p
3
5p
4
p
3
p
4
f (x) sin(x)
g
(
x
)
cos
(
x
)
m Figure 7
442 Chapter
5 The Integral
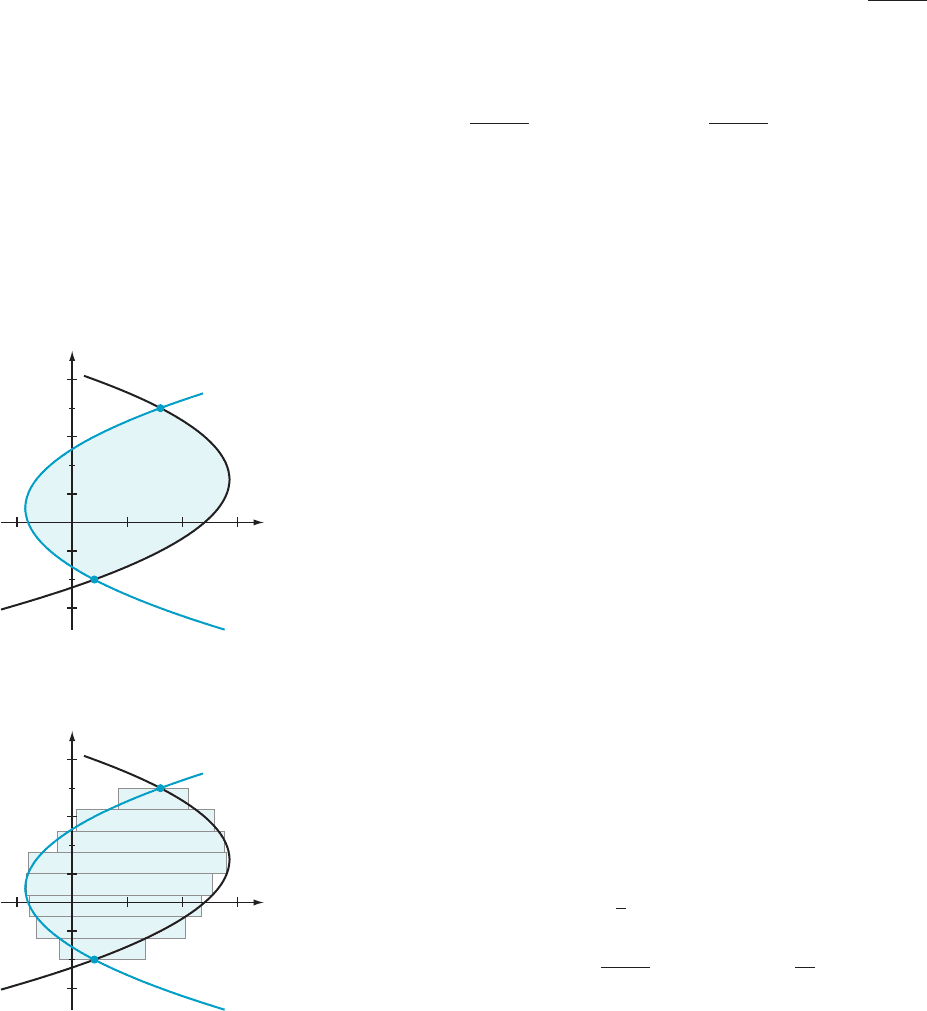
Z
5π=4
π=4
sinðxÞ2 cosðxÞ
dx 5
2cosðxÞ2 sinðxÞ
5π=4
π=4
5 2
ffiffiffi
2
p
:
On [5π/4, 5π/3], cos(x) $ sin(x). The corresponding area is, thus,
Z
5π=3
5π=4
cosðxÞ2 sinðxÞ
dx 5
sinðxÞ1 cosðxÞ
5π=3
5π=4
5
ffiffiffi
2
p
1
1 2
ffiffiffi
3
p
2
:
Adding the three areas that we have computed gives the total area between the
curves:
ffiffiffi
2
p
1
ffiffiffi
3
p
2 1
2
1 ð2
ffiffiffi
2
p
Þ1
ffiffiffi
2
p
1
1 2
ffiffiffi
3
p
2
5 4
ffiffiffi
2
p
: ¥
Reversing the Roles
of the Axes
To calculate the area between certain pairs of curves, it is convenient to inter-
change the roles of the x-axis and the y-axis. Consider the following example.
⁄ EX
AMPLE 6 Compute the area between the curves x 5 y
2
2 y 2 4and
x 52y
2
1 3y 1 12.
Solution The
curves in question are parabolas. By setting the expressions for x
equal to each other, we obtain
y
2
2 y 2 4 52y
2
1 3y 1 12;
or
y
2
2 2y 2 8 5 0:
The roots are y 522 and y 5 4. The parabolas intersect at (2, 22) and (8, 4).
Figure 8 exhibits this information, as well as the region whose area we wish to
calculate.
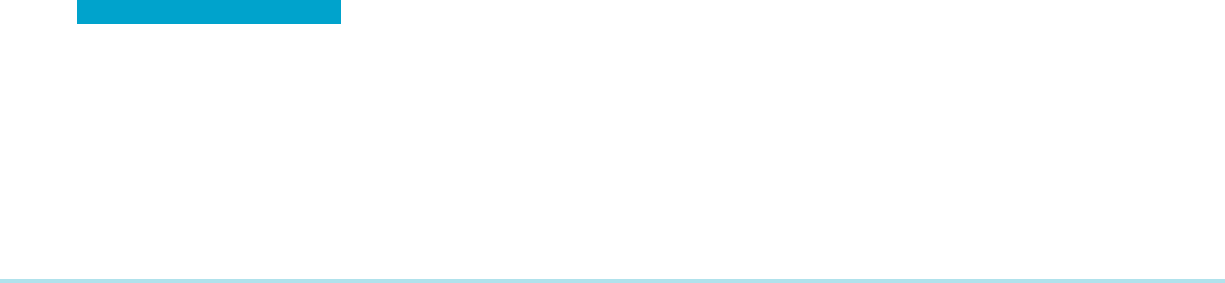
If we were to calculate the area of the region using an x-integral, then we would
need to solve for the upper and lower branch of each parabola, which would make
the algebra complicated. Instead, we think of x as a function of y and approximate
the area by horizontal rectangles (see Figure 9). Reasoning as before, we are led to
consider the integral
Z
4
22
ð2 y
2
1 3y 1 12Þ2 ðy
2
2 y 2 4Þ
dy:
Notice that we subtract the expression describing the parabola on the left from
that describing the parabola on the right—this corresponds to subtracting lesser
x-coordinates from greater x-coordinates, so that we will be computing the positive
area. Simplifying the integrand of the last integral and then integrating term by
term, we obtain
Z
4
22
ð22y
2
1 4y 1 16Þdy 5
2
2
3
y
3
1 2y
2
1 16y
y5 4
y522
5
2128
3
1 32 1 64
2
16
3
1 8 2 32
5 72
for the area between the two parabolas.
¥
y
x
5155
5
3
3
(8, 4)
x y
2
3y 12
x y
2
y 4
m Figure 9
y
x
5155
5
3
1
3
(8, 4)
(2, 2)
x y
2
3y 12
x y
2
y 4
m Figure 8
5.7 More on the Calculation of Area 443
QUICK QUIZ
1. Suppose that f and g are continuous functions on [a, b] with g(x) # f (x) for every
x in [a, b]. The area of the region that is bounded above and below by the
graphs of f and g, repectively, is equal to
R
b
a
hðxÞdx for what expression h (x)?
2. What is the area between the x -axis and the curve y 5 sin(x) for 0 # x # 2π?
3. What is the area between the y-axis and the curve x 5 1 2 y
2
?
4. The area of a region is obtained as
R
2
0
ð4 2 x
2
Þdx by integrating with respect to x.
What integral represents the area if the integration is performed with respect to y?
Answers
1. f (x) 2 g (x)
2. 4 3. 4/3 4.
R
4
0
ffiffiffiffiffiffiffiffiffiffiffi
4 2 y
p
dy
EXERCISES
Problems for Practice
c In each of Exercises 1212, a function f is defined on a
specified interval I 5 [a, b]. Calculate the area of the region
that lies between the vertical lines x 5 a and x 5 b and
between the graph of f and the x-axis. b
1. f (x) 5 2
cos(x) I 5 [π/4, 2π/3]
2. f (x) 5 3x
2
2 3x 2 6 I 5 [22, 4]
3. f (x) 5 2x
2
28 I 5 [23, 5]
4. f (x) 5 4/x 2 xI5 [1, 3]
5. f (x) 5 x
3
1 x 1 2 I 5 [22, 1]
6. f (x) 5 x/(x
2
1 1)
2
I 5 [21, 3]
7. f (x) 5 8x (1 2 x
2
)
2
I 5 [21/2, 1]
8. f (x) 5 exp(x) 2 eI5 [21, 2]
9. f (x) 5 x (4 2 x
2
)
3
I 5 [22, 3]
10. f (x) 5 (x
2
2 1)(x 2 2) I 5 [22, 2]
11. f (x) 5 12 2 9x 2 3x
2
I 5 [22, 2]
12. f (x) 5 8x 2 5/(1 1 x
2
) I 5 [21, 2]
c In each of Exercises 13218, a function f is
defined piece-
wise on an interval I 5 [a, b]. Find the area of the region that
is between the vertical lines x 5 a and x 5 b and between the
graph of f and the x-axis. b
13.
f ðxÞ5
(
2x
2
if 23 # x # 1
2x 2 3if1, x # 4
I 5 ½2 3; 4
14.
f ðxÞ5
(
2x 1 3if22 # x , 0
2x
2
1 3x 1 3if0# x # 3
I 5 ½22; 3
15. f ðxÞ5
(
sinðxÞ if 0 # x # π=4
cosðxÞ if π=4 , x # π
I 5 ½0; π
16.
f ðxÞ5
(
x 2 2if0# x # 2
sinðπxÞ if 2 , x # 4
I 5 ½0; 4
17. f ðxÞ5
(
4 2 x
2
if 22 # x # 3
x
2
2 8x 1 10 if 3 , x # 6
I 5 ½22; 6
18.
f ðxÞ5
(
secðxÞ if 0 # x # π=3
4 cosðxÞ if π=3 , x # π
I 5 ½0; π
c In each of Exercises 19226, find the area of the region
that
is bounded by the graphs of y 5 f (x) and y 5 g(x) for x
between the abscissas of the two points of intersection. b
19. f (x) 5 x
2
2 1 g(x) 5 8
20. f (x) 5 15/(1 1 x
2
) g(x) 5 3
21. f (x) 5 x
2
1 x 2 1 g(x) 5 2x 1 1
22. f (x) 5 2x 1 3 g(x) 5 9 1 x 2 x
2
23. f (x) 5 x
2
1 x 1 1 g(x) 5 2x
2
1 3x 2 7
24. f (x) 5 x
2
g(x) 522x
2
2 15x 2 18
25. f (x) 5 x
2
1 5 g(x) 5 2x
2
1 1
26. f (x) 5 x
2
1 5x 1 9 g(x) 52x
2
1 19x 2 15
c In each of Exercises 27230, the graphs of y 5 f (x)
and
y 5 g(x) intersect in more than two points. Find the total area
of the regions that are bounded above and below by the
graphs of f and g. b
27. f (x) 5 x
3
2 3x
2
2 x 1 4 g(x) 523x 1 4
28. f (x) 5 x
3
1 x
2
g(x) 5 x
2
1 x
29. f (x) 5 x
4
2 5x
2
g(x) 524
30. f (x) 5 2 sin(x) g(x) 5 6(π 2 x)/(5π)
c In each of Exercises 31234, determine the area between
the
two curves over the range of x. b
31. f ðxÞ52
ffiffi
ffi
3
p
cosðxÞ gðxÞ5 sinðxÞ; 2π # x # 2π=3
32. f ðxÞ5
ffiffiffi
3
p
sinðxÞ gðxÞ5 cosðxÞ; 2π=2 # x # 7π=6
33. f ðxÞ5 sinð2xÞ gðxÞ5 cosðxÞ; 0 # x # π=2
34. f ðxÞ5 cosð2xÞ gðxÞ5 sinðxÞ; 2π=2 # x # π=2
c In Exercises 35240, treat the y variable
as the independent
variable and the x variable as the dependent variable. By
integrating with respect to y, calculate the area of the region
that is described. b
35. The
region between the curves x 5 y
2
and x 52y
2
1 4
36. The region between the curves y 5 x and x 5 y
2
2 2
37. The region between the curves x 5 cos( y) and x 5 sin( y),
π/4 # y # 5π/4
38. The region between the curves x 5 y
2
1 1 and x 1 y 5 3
444 Chapter 5 The Integral
