Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

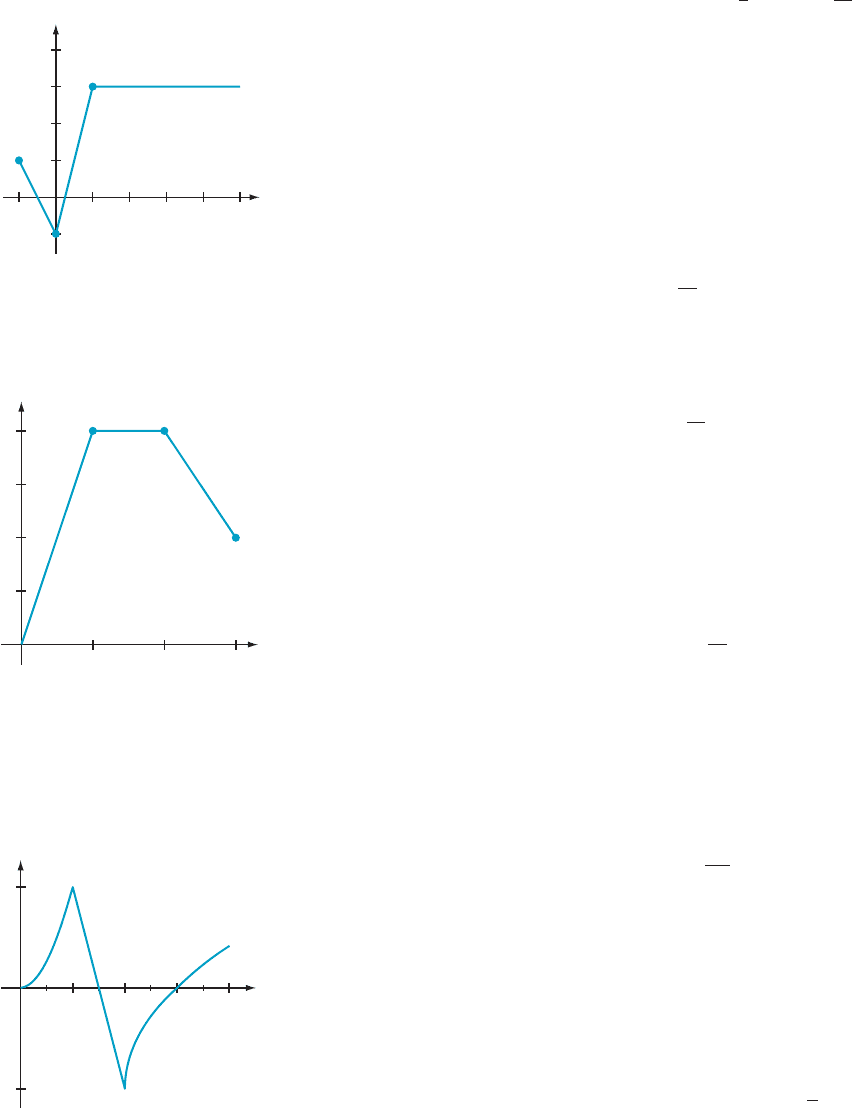
54. Calculate FðxÞ5

f ðtÞdt where f is the function with

the graph that appears in Figure 5.

55. Find a function f such that FðxÞ5

f ðtÞdt for the func-

tion F with the graph that appears in Figure 6.

56. For the function f shown in Figure 7, determine on what

interval(s) FðxÞ5

f ðtÞdt is increasing, decreasing,

concave up, and concave down.

57. Consider the integration

dt 52



Integrating a positive function from left to right should

not result in a negative number. What error has led to the

incorrect negative answer?

58. The Fundamental Theorem of Calculus guarantees the

existence of a function F with a derivative of |x|. Write an

explicit formula for F. Your formula should contain no

integrals.

59. Let g and h be differentiable functions, and let f be a

continuous function. Suppose that the range of h is con-

tained in the domain of g. Find a formula for

gðhðxÞÞ

f ðtÞdt:

60. Let g and h be differentiable functions, and let f be a

continuous function. Use the method of Example 6 to ﬁnd

a formula for

gðxÞ

hðxÞ

f ðtÞdt:

61. Suppose that f is a differentiable function with continuous

derivative f

. What is the average rate of change of the

function f over the interval [a, b]? (Refer to Section 3.1 in

Chapter 3, if necessary.) What is the average value of f

over [a, b]? (Refer to Section 5.3, if necessary.) Prove that

these two quantities are equal.

62.

GðaÞ5

f ðtÞdt



x5 0

What is G

(a)?

63. Suppose f and g are functions with continuous derivatives

on an interval containing [a, b]. Prove that if f (a) # g (a)

and if f

(x) # g

(x) for all x in [a, b], then f (x) # g (x) for

all x in [a, b].

64. In probability and statistics, the error function (erf) is

deﬁned for x $ 0by

erfðxÞ5

ﬃﬃﬃ

expð2t

Þdt:

Show that the graph of erf is concave down over [0, N).

65. Dawson’s integral is the function deﬁned for x $ 0by

FðxÞ5 expð2x

expðt

Þdt:

Compute F

(x).

66. The Fresnel sine integral, deﬁned by

Fresnel SðxÞ5

sin





dt;

4.03.02.0

1.0

1

m Figure 7

112

(0, 1)

(1, 1)

(1, 3)

345

m Figure 5

2.0

0.5

(1, 2) (2, 2)

(3, 1)

1.0

1.5

m Figure 6

5.4 The Fundamental Theorem of Calculus 415

is an important function in the theory of optical diffrac-

tion. Determine the intervals on which this function is

concave up.

67. The function

CðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 t

dt ðx $ 0Þ

arises in the computation of pressure within a white

dwarf. Show that C is an increasing function with a graph

that is concave up.

68. The sine integral is the function Si, deﬁned by Sið xÞ5

sinðtÞ=tdt: Calculate lim

x-0

SiðxÞ=x.

69. Let f be continuous on an interval I that contains a and b.

For x in I set FðxÞ5

f ðtÞdt and GðxÞ5

f ðtÞdt: Use

the Fundamental Theorem of Calculus to show that there

is a constant C such that F 5 G 1 C. Using Theorem 3

from Section 5.3 to give a second proof.

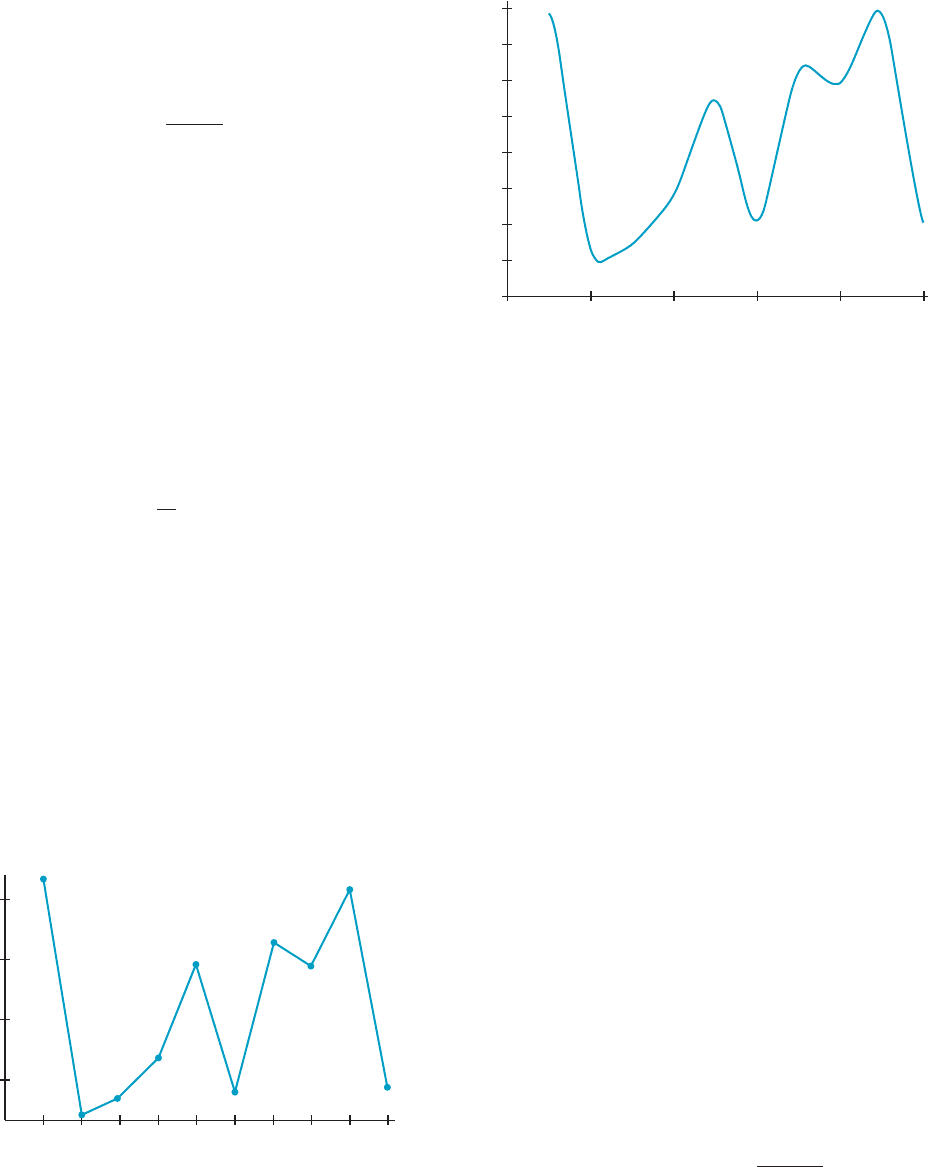
c Averaging data smooths it out. The Mean Value Theorem

for

Integrals tells us that for a ﬁxed h, we can think of the

integral

ðxÞ5

x1h

x2h

f ðtÞdt

as an operation that averages the values of f over the interval

[x 2 h, x 1 h]. Figure 8 shows a plot of the price f of one share of

Microsoft’s stock at the close of ten consecutive trading days in

the summer of 2009. Figure 9 shows a plot of the average price

that is obtained by using h 5 1/4. (This choice of h is arbi-

trary.) In each of Exercises 70272,

calculate and plot A

over

[21, 1] for the given function f and h 5 1/2. b

70. f (x) 5 |x|

71. f ðxÞ5 f

fx , 0

x if 0 # x

72. f (x) 5 signum(x)

73. Let f (x) 5 bx c be the greatest integer function. Show that

FðxÞ5

f ðtÞdt

is not differentiable at x 5 1.

74. Let b be a constant, and set

f ðtÞ5

0ift , 0

x 1 b if 0 # t



Show that F (x) 5

f ðtÞdt is continuous at x 5 0 for all

values of b but differentiable at x 5 0 only if b 5 0.

Calculator/Computer Exercises

c In Exercises 75278, plot F

and F

. Determine the

intervals on which F is increasing, decreasing, concave up,

and concave down. b

75. FðxÞ5

ðt

2 3t

1 3t 1 4Þdt

76. f ðxÞ5

ðt 1 1Þ=ðt

1 1Þdt

77. FðxÞ5

ðt

2 tÞe

78. FðxÞ5

ðt

2 3Þ lnðtÞdt x . 0

79. In a particular regional climate, the temperature varies

between 228



C and 46



C and averages 13



C. The number

of days N (T) in the year on which the temperature

remains below T degrees centigrade is given (approxi-

mately) by

NðTÞ5

228

f ðxÞdx ð228 # T # 46Þ

where

f ðxÞ5 12:66 exp



ðx2 13Þ

265:8



23.3

23.4

23.5

23.6

23.7

23.8

23.9

23.2

Microsoft share price (dollars), smoothed by integrating

Jul

1, 2009—Jul

10, 2009

246810

m Figure 9

23.4

246810

July 1, 2009—July 10, 2009

23.6

Microsoft share price (dollars)

23.8

24.07

23.28

23.34

23.47

23.35

23.77

23.37

23.79

23.86

24.04

m Figure 8

416 Chapter

5 The Integral

Plot y 5 N (T) for 228 # T # 46. On about how many days

does the temperature reach at least 37



80. Find positive numbers a and b for which the sine integral

deﬁned in Exercise 68 is concave down on the interval

(0, a), concave up on the interval (a, b), and concave down

again just to the right of b.

81. The Fresnel sine integral, FresnelS, is deﬁned in Exercise

66. The Fresnel cosine integral, FresnelC, is deﬁned

analogously with cos





replacing sin





. Plot the

parametric equations x 5 FresnelC(t), y 5 FresnelS(t) for

0 # t # 6. (Your plot is an arc of a curve that is known as

the Cornu spiral.)

c In each of Exercises 82285, a function f and

a point c are

given. Let F be deﬁned by formula (5.4.2) with a 5 1/4. (This

assignment of a is for the sake of being deﬁnite. A different

value would not change anything in these exercises.) For

h 5 0.001, numerically calculate

c1h=2

c2h=2

f ðtÞdt, and use this

value to obtain a central difference quotient approximation of

(c). Use the value of f (c) together with equation (5.4.6) to

verify your approximation of F

(c). b

82. f ðtÞ5 cosðπt

Þ c 5 1

83. f ðtÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 t

c 5 2

84. f ðtÞ5 t

t21

c 5 3

85. f ðtÞ5

ﬃﬃ

t24

c 5 4

5.5 A Calculus Approach to the Logarithm and

Exponential Functions

In this section, we take a second look at exponential and logarithm functions. In

our new approach, we use calculus to deﬁne the exponential and logarithm func-

tions and to develop their properties. In doing so, we can ﬁll in some details that so

far have been missing. Of course, everything you will learn in this section is con-

sistent with the notions we have already developed.

First, let us summarize our previous approach. In Section 2.6 of Chapter 2, we

introduced the special base

e 5 lim

n-N





ð5:5:1Þ

and demonstrated that

5 lim

n-N





ð5:5:2Þ

for all u. In Section 3.4 of Chapter 3, we used formula (5.5.2) to prove that

5 e

We then deﬁned the natural logarit hm to be the inverse function of the exponential

function and derived the formula

lnðxÞ5

from the Inverse Function Derivative Rule.

The approach that we have summarized is a valid one, but it depends on

formula (5.5.1), which we did not prove. It is instructive to see how calculus can be

applied to ﬁnesse such difﬁculties. For the purposes of this section we will put aside

everything that we have learned about the exponential and logarithm functions and

redevelop these functions from scratch . Our point of departure is to deﬁne the

natural logarithm function by the construction that is the subject of the second part

of the Fundamental Theorem of Calculus:

5.5 A Calculus Approach to the Logarithm and Exponential Functions 417

lnðxÞ5

dt ; 0 , x , N: ð5:5:3Þ

For x . 1, it is perfectly all right to think of ln(x) as the area of the region that

lies under the graph of y 5 1/t and above the interval [1, x] (Figure 1). For

0 , x , 1, the value ln (x) is the negative of the area between the graph and the x-

axis (because in this case the integration of the positive integrand 1/t is from right

to left). See Figure 2. As you look at Figures 1 and 2, imagine sliding the point

labeled x to the left or to the right on the horizontal axis. The area of the shaded

region will certainly change. That is the functional relationship captured by for-

mula (5.5.3). Although this deﬁnition of the natural logarithm may not be an

intuitive one, it does lead quickly to the properties of the logarithm that we

require. Indeed, a number of basic facts about the natural logarithm can be

deduced immediately.

THEOREM 1

The natural logarithm has the following properties:

a. If x . 1, then ln(x) . 0.

b. If x 5 1, then ln(x) 5 0.

c. If 0 , x , 1, then ln(x) , 0.

d. The natural logarithm has a continuous derivative:

lnðxÞ5

; 0 , x:

e. The natural logarithm is an increasing function: ln (x

) , ln (x

)if0, x

, x

Proof. Pa

rts a and c may be understood geometrically in terms of areas, as has

been discussed. Part b follows from Theorem 1d of Section 5.3. The derivative

formula of part d is equation (5.4.6) with f (t) 5 1/t. Finally, we deduce that ln (x)is

an increasing function of x because its derivative 1/x is everywhere positive . ’

As the computation in Example 2 from Section 4.9 of Chapter 4 shows, the

rivative formula of Theorem 1d can be generalized to

lnðjxjÞ5

;

which is true for all x 6¼0. Therefore the equation

dx 5 lnðjxjÞ1 C

is the preferred antiderivative formulation of Theorem 1d.

Properties of the

Natural Logarithm

Using deﬁnition (5.5.3), we can derive many useful properties of the natural

logarithm.

THEOREM 2

Let x and y be positive. Then

lnðx  yÞ5 lnðxÞ1 lnðyÞ; ð5:5:4Þ

(1, 1)

y 





m Figure 2 ln(x)=2A(0 , x, 1)

y 

(1, 1)





m Figure 1 ln(x)=A

418 Chapter 5 The Integral





52lnðxÞ; ð5:5:5Þ





5 lnðxÞ2 lnðyÞ; ð5:5:6Þ

and, for any number p,

lnðx

Þ5 p  lnðxÞ : ð5:5:7Þ

Proof. To

obtain identity (5.5.4) , we ﬁx y and use the Chain Rule to calculate

lnðxyÞ5



ðxyÞ5

 y 5

In other words, for each ﬁxed y, ln(xy) is an antiderivative of 1/x. Because ln(xy )

and ln(x) are antiderivatives of the same expression, 1/x, it follows that

lnðxyÞ5 lnðx Þ1 C ð5:5:8Þ

for some constant C. By setting x 5 1 in equation (5.5.8), we see that ln( y) 5 0 1 C,

or C 5 ln( y). Substituting this value for C in equation (5.5.8) yields (5.5.4).

Next, we set y 5 1/x in equation (5.5.4), obtaining

lnðxÞ1 ln





5 ln



x 



5 lnð1Þ5 0;

which is equivalent to equation (5.5.5). To obtain equation (5.5.6), we write x/y as

x  (1/y) and use equations (5.5.4) and (5.5.5) as follows:





5 ln



x 



ð5:5:4Þ

lnðxÞ1 ln





ð5:5:5Þ

lnðxÞ2 lnðyÞ:

Equation (5.5.7) is proved in several stages. As you read the demonstration,

notice how earlier steps are used to prove later steps. First, if p 5 0, then ln(x

) 5

ln(1) 5 0 5 0 ln(x). Thus equation (5.5.7) is true for p 5 0. Next observe that

lnðx

Þ5 lnðx  xÞ5 lnðxÞ1 lnðxÞ5 2  lnðxÞ:

Similarly,

lnðx

Þ5 lnðx

 xÞ5 lnðx

Þ1 lnðxÞ5 2  lnðxÞ1 lnðxÞ5 3lnðxÞ

This idea can be repeated, showing that (5.5.7) holds for every positive integer.

Now suppose that p is a negative integer. Then p 52|p| with |p| a positive integer.

By the positive integer case of (5.5.7), which has just been proved, we have



ðx

jpj



5 jpjlnðx

Þ:

As a result,

lnðx

Þ5 lnðx

2jpj

Þ5 ln



ðx

jpj



5 jpjlnðx

Þ5 jpjln





ð5:5:5Þ

2jpjlnðxÞ5 p lnðxÞ:

This equation completes the proof that identity (5.5.7) is valid for all integers p.

Now suppose that p is a rational number. That is, suppose that there are tw o

5.5 A Calculus Approach to the Logarithm and Exponential Functions 419

integers m and n 6¼0 such that p 5 m/n. Then, using the integer case of (5.5.7) twice,

we have

m  lnðxÞ5 lnðx

Þ5 lnðx

pn

Þ5 ln



ðx



5 n  lnðx

Þ:

By dividing the ﬁrst and last terms in this chain of equalities by n, we obtain (m/n) 

ln(x) 5 ln(x

), or p  ln (x) 5 ln(x

). We have now proved that equation (5.5.7)

holds for all rational values of p. Later in this section, we will rigorously deﬁne

irrational exponents in a way that ensures the validity of property (5.5.7) for

irrational values of p as well. ’

Graphing the Natural

Logarithm Function

Now we examine the graph of y 5 ln (x). We have already learned that the natural

logarithm is an increasing function with x -intercept 1 (Theorem 1e and 1b).

Because

lnðxÞ5





, 0;

we infer that the graph of the natural logarithm is concave down. There are no

relative maxima or minima because the derivative 1/x is never 0.

Let us now investigate the behavior of ln(x)asx tends to inﬁnity. Because the

natural logarithm is an increasing function, ln(x) either increases to a ﬁnite bound

as x tends to inﬁnity or ln(x) increases without bound. We can rule out the ﬁrst

possibility by considering the sequence fln(2

)g. Because 2 . 1, we deduce that

ln(2) . ln(1) 5 0. Therefore

lnð2

Þ 5

ð5:5:7Þ

n  lnð2Þ-N:

We conclude that

lim

x-N

lnðxÞ5 N:

We can complete our sketch of y 5 ln(x) for 0 , x ,N by investigating the behavior

as x- 0

. In fact, a change of variable allows us to determine the behavior at 0

from the limit at inﬁnity:

lim

x-0

lnðxÞ 5

u5 1=x

lim

u-1 N





ð5:5:5Þ

2 lim

u-N

lnðuÞ52N:

In other words, the y-axis is a vertical asymptote. A sketch of the graph of y 5 ln(x)

appears in Figure 3.

Because x 7!ln(x) is a continuous function that takes on arbitrarily large

positive and negative values, the Intermediate Value Theorem (Section 2.3 of

Chapter 2) tells us that the equation ln(x) 5 γ has a solution for each real number γ.

Because the natural logarithm is an increasing function, the solution is unique. We

summarize our ﬁndings in Theorem 3.

THEOREM 3

The natural logarithm is an increasing funct ion with domain

equal to the set of positive real numbers. Its range is the set of all real numbers.

The equation ln(x) 5 γ has a unique solution x A R

for every γ A R. The graph

of the natural logarithm function is concave down. The y-axis is a vertical

asymptote.

y  ln(x)

m Figure 3

420 Chapter

5 The Integral

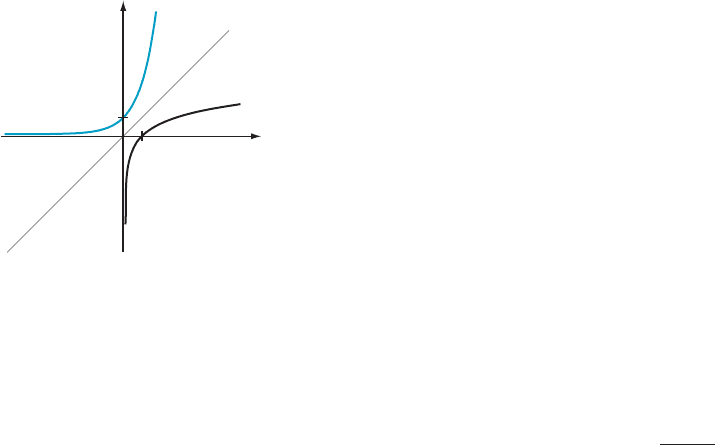
The Exponential

Function

In the preceding subsect ion, we de duced that the equation ln(x) 5 γ has a unique

positive solution x for every real number γ. In other words, the natural logarithm is

an invertible function with domai n R

and image R. The inverse of the natural

logarithm is called the exponential function (or natura l expo nential function) and is

written x 7! exp (x). The domain of the exponential function is the entire real line;

the image of the exponential function is the set of positive real numbers.

Recall that, when we say that the exponential function is the inverse function of

the natural logarithm, we mean that a real number a and a positive number b are

related by the equation

b 5 expðaÞ

if and only if

a 5 lnðbÞ

We may also exp ress the inverse relationship between the natural exponential and

logarithm functions as follows:

lnðexpðaÞÞ5 a for all a and expð lnðbÞÞ5 b for all b . 0:

Before continuing, remember that we have started from scratch in this section. In

the current approach, we do not yet have the number e. The idea is to use the

exponential function to deﬁne e. After that is done, we will show that exp(x) 5 e

These developments, however, are still ahead.

Properties of the

Exponential Function

The graph of y 5 exp(x ) appears in Figure 4. It is obtained by reﬂecting the graph of

y 5 ln(x) through the line y 5 x. (Recall that this is the general procedure for ﬁnding

the graph of an inverse function.) Because the graph of y 5 ln(x) lies below the line

y 5 x and is concave down and rising, we conclude that the graph of y 5 exp(x) lies

above the line y 5 x and is concave up and rising. In particular, the natural expo-

nential is an increasing function. Because ln(1) = 0, it follows that exp(0) 5 1. In other

words, 1 is the y-intercept of the graph of y 5 exp(x). The exponential function only

assumes positive values, so there is no x-intercept.

Next, we turn to some of the algebraic properties of the exponential function.

The basic exponential law is

expðs 1 tÞ5 expðsÞexpðtÞ; ð5:5:9Þ

which holds for all real numbers s and t. Identity (5.5.9) is the analogue of equation

(5.5.4) for the logarithm, from which it can be derived. Indeed, notice that

lnðexpðs 1 tÞÞ5 s 1 t 5 lnðexpðsÞÞ1 lnðexpð tÞÞ 5

ð5:5:4Þ

lnðexpðsÞexpðtÞÞ

Because the natural logarithm is a one-to-one function, it follows that exp (s 1 t)

must equal exp (s)  exp (t), as identity (5.5.9) asserts.

A few other useful identities can be obtained from equation (5.5.9). For

instance, when s equals 2t, equation (5.5.9) becomes exp (0) 5 exp (2t) exp(t)or

expð2tÞ5

expðtÞ

; ð5:5:10Þ

which is the analogue of logarithm identity (5.5.5). Formulas (5.5.9) and (5.5.10)

can be combined to produce

y  ln(x)

y  exp(x)

y  x

m Figure 4

5.5 A Calculus Approach to the Logarithm and Exponential Functions 421

expðs 2 tÞ5

expðsÞ

expðtÞ

; ð5:5:11Þ

which is the analogue of logarithm identity (5.5.6). Finally, we obtain the expo-

nential version of logarithm equation (5.5.7) by noting that

lnðexpðsÞ

Þ 5

ð5:5:8Þ

t lnðexpðsÞÞ5 ts 5 st 5 lnðexpðstÞÞ:

Because the logarit hm is one-to-one, we deduce that

ðexpðsÞÞ

5 expðstÞð5:5:12Þ

for all real s and t.

Derivatives and

Integrals Involving the

Exponential Function

Just as the algebraic properties of the exponential function follow from corre-

sponding properties of the logarithm, so too can the calcu lus properties of the

exponential function be deduced from their logarithm counterparts.

THEOREM 4

The exponential function satisﬁes

expðxÞ5 expðxÞ and

expðxÞdx 5 expðxÞ1 C:

More generally,

expðuÞ5 expðuÞ

and

expðuÞ

dx 5 expð uÞ1 C:

Proof. Wh

en we studied inverse functions in Section 3.6 of Chapter 3, we learned

that, if g is the inver se function of f,iff is differentiable at g (c), and if f

ðgðcÞÞ 6¼ 0;

then g is differentiable at c, and

ðcÞ5

ðgðcÞÞ

Let g (x) 5 exp(x) and f (x)= ln(x). Then

expðxÞ



x5 c

lnðxÞ



x5 exp ðcÞ



x5 exp ðcÞ

1=expðcÞ

5 expðcÞ:

In other words,

expðxÞ5 expðxÞ;

which is the ﬁrst assertion. The other assertions follow from this one. ’

The Number e In our present approach, we deﬁne the number e by the simple equation

e 5 expð1Þ: ð5:5:13Þ

See Figure 5a. Applying the natural logarithm to each side of equation (5.5.13) and

using the inver se relationship of the natural logarithm and exponential functions,

we obtain

422 Chapter 5 The Integral

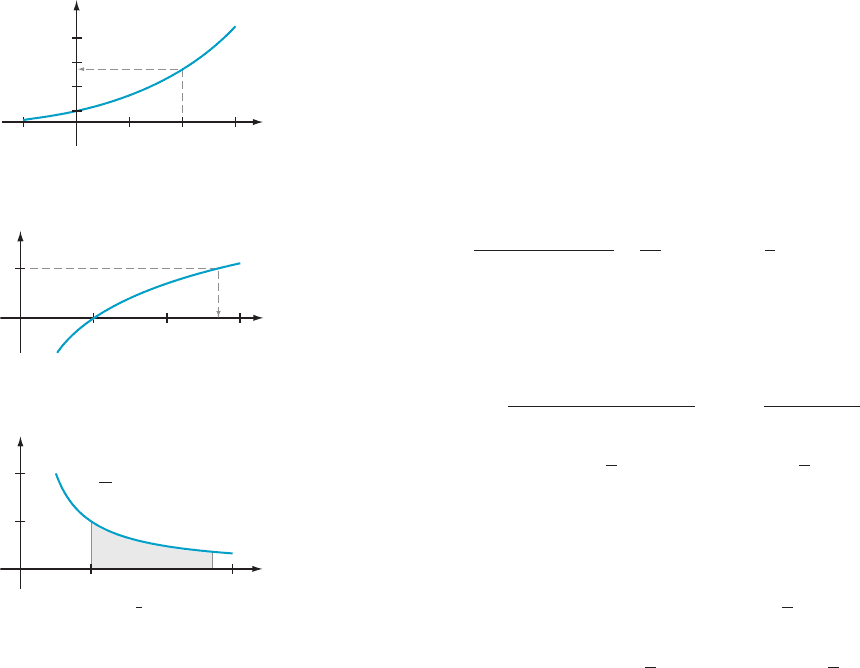
lnðeÞ5 1 : ð5:5:14Þ

See Figure 5b. By noting that ln(e) 5

1=xdx; we see that e is the number such

that the area under the graph of y 5 1/x and over the interval [1, e] is 1. Figure 5c

illustrates this third representation of the number e.

One advantage of the present development is that we can derive equation

(5.5.1) in a few steps. To do so, we ﬁrst examine the deﬁnition of the derivative of

ln(x)atx 5 1:

lim

h-0

lnð1 1 hÞ2 lnð1Þ

lnðxÞ



x5 1



x5 1

5 1:

In this equation, we will let h 5 1/n where n tends to inﬁnity through positive

integers. Thus

1 5 lim

n-N



1 1 ð1=nÞ



2 lnð1Þ

1=n

5 lim

n-N

lnð1 1 1=nÞ

1=n

5 lim

n-N

n ln



1 1



ð5:5:7Þ

lim

n-N





Now we exponentiate both sides of this equation and use the continuity of the

exponential function to obtain

e 5

ð5:5:13Þ

expð1Þ5 exp



lim

n-N



1 1





5 lim

n-N

exp





1 1





5 lim

n-N



1 1



;

which is formula (5.5.1).

Logarithms and Powers

with Arbitrary Bases

Until now, we have understood a

to be a limit when the value of x is irrational. In

our new treatment, we use the logarithm and exponential functions to deﬁne a

in a

more elegant way. To do so, we observe that, for any positive number a and any

rational number x,

5 expðlnða

ÞÞ 5

ð5:5:7Þ

expðx  lnðaÞÞ: ð5:5:15Þ

Notice that the right side of equation (5.5.15) is meaningful even when x is irra-

tional. We therefore deﬁne a

for any real number x by

5 expðx  lnðaÞÞ ðx 2 RÞð5: 5 :16Þ

Bear in mind that equation (5.5.16) extends the deﬁnition of exponentiation to

irrational values of x and agrees with the elementary, algebraic notion of expo-

nentiation when x is rational.

As an immediate consequence of this extension, we see that

lnða

Þ5 lnðexpð x  lnðaÞÞÞ5 x  lnðaÞ

1.50.5 1

0.5

y  exp(x)

m Figure 5a e = exp(1)

y  ln(x)

321

m Figure 5b ln(e)=1

Area  1

y 

m Figure 5c

dx 5 1

5.5 A Calculus Approach to the Logarithm and Exponential Functions 423

which shows that formula (5.5.7) is valid even for irrational values of x. As the next

example shows, it is easy to use deﬁnition (5.5.16) when working with exponents.

⁄ EX

AMPLE 1 Use formula (5.5.16) to derive the Power Rule of differ-

entiation:

5 p  x

p21

Solution Since

Chapter 3, we have used this basic differentiation rule without

veriﬁcation. Now we can prove it as follows:



exp



p  lnðxÞ





ðby ð5:5:16ÞÞ

5 exp



p  lnðxÞ







p  lnðxÞ



ðChain RuleÞ

5 exp



p  lnðxÞ







p 



5 x





p 



ðby ð5:5:16ÞÞ

5 p  x

p21

: ðalgebraic simplificationÞ ¥

Notice that when a is

taken to be e, we have ln(a) 5 ln(e) 5 1 by equation

(5.5.14). As a result, formula (5.5.16) simpliﬁes to

5 expðxÞ:

We may use this observation to rewrite equation (5.5.16) as

5 e

xlnðaÞ

: ð5:5:17Þ

The laws of exponents can all be quickly derived from equation (5.5.14) and

the corresponding properties of the exponential function. We state these laws in the

next theorem and leave their proofs as Exercises 5356.

THEOREM 5

(Laws of Exponents)Ifa, b . 0, and x, y A R, then

a. a

5 1

b. a

5 a

c. a

x1y

5 a

 a

d. a

x2y

e. (a

)

5 a

x y

f. a

5 b if and only if b

1/x

5 a ( provided x 6¼0)

g. (a  b)

5 a

 b

Logarithms with

Arbitrary Bases

If a is any positive number other than 1, then we deﬁne the logarithm function log

with base a by

log

ðxÞ5

lnðxÞ

lnðaÞ

ðx 2 R

Þ: ð5:5:18Þ

424 Chapter 5 The Integral