Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.

Notice that ln(a ) makes sense in (5.5.18) because a is assumed to be positive.
Furthermore, because we have made the assumption a 6¼1, ln(a) is nonzero, and the
division in equation (5.5.18) is permitted. Observe that log
e
(x) reduces to the
natural logarithm ln(x) because ln(a) 5 1 when a 5 e.
THEOREM 6
For any fixed positive a 6¼1, the function x 7!a
x
has domain R and
image R
1
. The function x 7!log
a
(x) has domain R
1
and image R. The two
functions satisfy the identities
a
log
a
ðyÞ
5 y ðy 2 R
1
Þ and log
a
ða
x
Þ5 x ðx 2 RÞ:
In words, the functions x 7!a
x
and y 7!log
a
( y) are inverse to each other.
Proof. We
obtain the inverse relationship between x 7! a
x
and y 7! log
a
( y) from
the inverse relationship between the natural logarithm and exponential functions.
For y . 0, we use equation (5.5.17) with x 5 ln( y)/ln(a) to obtain
a
log
a
ðyÞ
5 a
lnðyÞ=lnðaÞ
5
ð5:5:17Þ
exp
lnðyÞ
lnðaÞ
lnðaÞ
5 expðlnðy ÞÞ5 y:
In the other direction, we have, for any x,
log
a
ða
x
Þ 5
ð5:5:18Þ
lnða
x
Þ
lnðaÞ
5
ð5:5:17Þ
lnðexpðx lnðaÞÞÞ
lnðaÞ
5
x lnðaÞ
lnðaÞ
5 x: ’
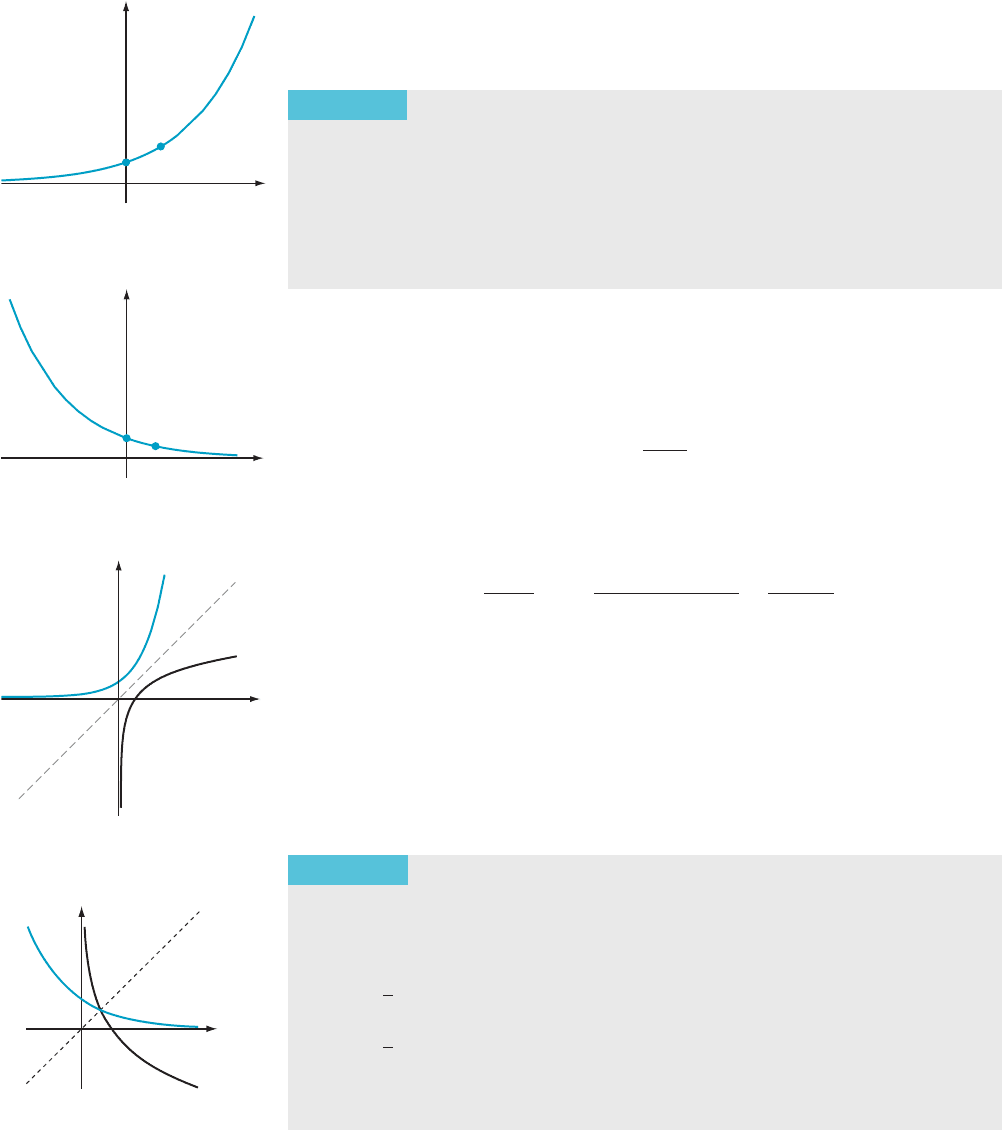
From Theorem 6 and the discussion of inverse functions in Section 1.5 of
Chapter
1, we see that the graphs of y 5 a
x
and y 5 log
a
(x) are reflections of each
other through the line y 5 x. Figures 6, 7, and 8 illustrate these reflections.
The laws of logarithms with arbitrar y bases can all be quickly derived from
equation (5.5.18) and the corresponding properties of the natural logarithm func-
tion. We state these properties in the next theo rem and leave their proofs as
Exercises 5760.
THEOREM 7
If x, y, a . 0, and a 6¼1, then
a. log
a
(a) 5 1
b. log
a
(1) 5 0
c. log
a
(xy) 5 log
a
(x) 1 log
a
( y)
d. log
a
1
x
52log
a
ðxÞ
e. log
a
x
y
5 log
a
ðxÞ2 log
a
ðyÞ
f. log
a
ðx
p
Þ5 plog
a
ðxÞ
y
y a
x
(0, 1)
(1, a)
x
m Figure 6 The graph of y 5 a
x
,
a . 1
y
x
y a
x
(0, 1)
(1, a)
m Figure 7 The graph of y 5 a
x
,
0 , a , 1
y log
a
(x)
The graph of y log
a
(x), 0 < a < 1
y x
y
y a
x
m Figure 8b
y log
a
(x)
y a
x
y x
x
y
m Figure 8a y 5 log a( x), 1 , a.
5.5 A Calculus Approach to the Logarithm and Exponential Functions 425

Differentiation and
Integration of a
x
and log
a
(x)
Differentiation formulas for a
x
and log
a
(x) are readily obtained from the deriva-
tives of exp(x) and ln(x) and the Chain Rule. For a fixed positive constant a 6¼1, we
have
d
dx
a
x
5 lnðaÞa
x
ð5:5:19Þ
and
d
dx
log
a
ðxÞ5
1
x lnðaÞ
: ð5:5:20Þ
We obtain formula (5.5.19) by setting u 5 x ln(a) and calculating with the Chain
Rule as follows:
d
dx
ða
x
Þ5
d
dx
e
xlnðaÞ
5
d
dx
e
u
5
d
du
e
u
du
dx
5 e
u
d
dx
ðx lnðaÞÞ5 e
xlnðaÞ
lnðaÞ5 a
x
lnðaÞ:
The derivation of (5.5.20) is straightforward:
d
dx
log
a
ðxÞ5
d
dx
lnðxÞ
lnðaÞ
5
1
lnðaÞ
d
dx
lnðxÞ5
1
lnðaÞ
1
x
:
Formula (5.5.19) is often combined with the Chain Rule and written in the form
d
dx
a
u
5 lnðaÞa
u
du
dx
: ð5:5:21Þ
Finally, it is useful to rewrite formula (5.5.19) in antiderivative form as
Z
a
x
dx 5
a
x
lnðaÞ
1 C:
QUICK QUIZ
1. Suppose that
R
a
1
1=tdt5 3 ; and
R
b
1
1=tdt5 5. What is
R
ab
1
1=tdt?
2. For what value of a is
R
a
1
1=tdt5 1?
3. Suppose that a is a positive constant. For what value of u is a
x
5 e
u
?
4. Suppose that a is a positive constant not equal to 1. For what value of k is
log
a
ðxÞ5 k lnðxÞ?
Answers
1. 8 2. e 3. x ln( a )
4. 1/ln(a)
EXERCISES
Problems for Practice
c In each of Exercises 1212, the numbers u and v satisfy
the equations
R
u
1
ð1=tÞdt 5 4 and
R
v
1
ð1=tÞ dt 5 12. Use these
equations, formula (5.5.3), and the properties of logarithms to
calculate the integral of 1/t over the given interval. b
1. [1,
1/u]
2. [1, ue]
3. [1, u/e]
4. [u,2u]
5. [3, 3u]
6. [1, uv]
7. [1, v/u]
8. [u, v]
9. [u, uv]
10. [1, v
2
]
11. [1, 2v]
12. [2u,2v]
c In each of Exercises 13230, calculate the derivative with
respect
to x of the given expression. b
426 Chapter 5 The Integral

13. ln(4x)
14. ln(23x)
15. ln(2x 1 3)
16. ln(sec (x))
17. ln(
ffiffiffiffiffiffiffiffiffiffiffi
1 2 x
p
)
18. ln(1/x)
19. 1/(4 1 ln(x))
20. ln(ln(x))
21. ln
2
(x)
22. 5
x
23. x2
x
24. 3
x
exp(x
2
)
25. 2
ln(x)
26. ln(1 1 3
x
)
27. log
10
(5/x)
28. log
5
(5 1 2x)
29. log
2
(3x)
30. log
2
(2 1 3
x
)
c In each of Exercises 31234, calculate the given definite
integral. b
31.
R
1
0
2
x
dx
32.
R
3
0
ð9=3
x
Þdx
33.
Z
1
0
1 þ 10
x
10
x
dx
34.
Z
1
0
2
x
þ 3
x
5
x
dx
Further Theory and Practice
c In each of Exercises 35242, calculate the first and second
derivatives of the given expression, and classify its local
extrema. b
35. 2
x
2 x
36. x2
x
37. x10
2x
38. log
2
(x) 2 x
39. xlog
10
(x)
40. log
3
(x)/x
41. ln
2
(x)
42. x
2
2 2 log
8
(x)
c In each of Exercises 43248, calculate the first and second
derivatives
of FðxÞ5
R
uðxÞ
a
f ðtÞdt for the given functions u and
f. b
43. u (x) 5 ln(x) f (t) 5 1/t
44. u (x) 5 log
2
(x) f (t) 5 1/t
45. u (x) 5 1/xf(t) 5 ln( t)
46. u (x) 5 2
x
f (t) 5 2
t
47. u (x) 5 ln(x) f (t) 5 ln(t)
48. u (x) 5 log
2
(x) f (t) 5 log
3
(t)
49. Let A and B be constants. Show that y 5 A cos(ln( x)) 1
B sin(ln(x)) is a solution of the equation
x
2
y
00
1 xy
0
1 y 5 0:
50. Suppose that a . 1. Let m be any positive number. Show
that the graph of y 5 log
a
(x) has a tangent line with slope m.
51. Show that
Z
1
jxj
dx 5 lnðjxjÞ1 C
is not a valid integration formula.
52. It is known that
R
e
1
lnðxÞdx 5 1: If a is a positive constant,
what is
R
e
1
lnðaxÞdx?
53. Let A and B be constants. Calculate the derivative of
A x lnðxÞ1 B x with respect to x. Show that there are
values of A and B such that
Z
lnðxÞdx 5 A xlnðxÞ1 B x 1 C
where C is an arbitrary constant.
54. Fix a positive h,andgraphf ðxÞ5 1=ð1 1 xÞ for 0 # x # h:
By comparing the area under the graph of f with an
inscribed rectangle and a circumscribed rectangle, show that
h
1 1 h
, lnð1 1 hÞ, h ð0 , hÞ:
55. Let f be a differentiable function that is defined on R
1
and that satisfies identity f (xy) 5 f (x) 1 f ( y). This exer-
cise outlines a proof that
f ðxÞ5 f
0
ð1ÞlnðxÞ:
a. By differentiating both sides of the given equation
with respect to x, treating y as constant, show that
f
0
(xy) y 5 f
0
(x).
b. By setting x 5 t and y 5 1/t in the equation obtained in
part a, show that f is an antiderivative of the function
t 7!f
0
(1)/t.
c. Use the result of part c to deduce that f (t) 5 f
0
(1)
ln(t) 1 C where C is a constant. By evalutating f (t)at
t 5 1, show that C 5 f (1).
d. By considering the given property of f with x 5 y 5 1,
deduce that f (1) 5 0.
56. Find the minimum value m of f (x) 5 x 2 ln(x). Use the
inequality x 2 ln(x) $ m to deduce that ln(1 1 x) # x
for 21 , x. Prove that there is no real value of x such that
ln(x) 5 x.
57. Use equations (5.5.16) and (5.5.9) to prove Theorem 5c.
58. Use equations (5.5.16) and (5.5.11) to prove Theorem 5d.
59. Use equations (5.5.16) and (5.5.12) to prove Theorem 5e.
60. Use equations (5.5.16), (5.5.4), and (5.5.9) to prove
Theorem 5g.
61. Use equations (5.5.18) and (5.5.4) to prove Theorem 7c.
62. Use equations (5.5.18) and (5.5.5) to prove Theorem 7d.
63. Use equations (5.5.18) and (5.5.6) to prove Theorem 7e.
5.5 A Calculus Approach to the Logarithm and Exponential Functions 427

64. Use equations (5.5.18) and (5.5.7) to prove Theorem 7f.
c Exercises 65273 concern a function called the Lambert
W
function, introduced in Exercise 61 and denoted here by W.
The Lambert W function is useful for the solution of many
equations involving exponentials and logarithms. b
65. Sh
ow that V :(21,N ) - (21/e,N ) defined by V (x) 5
x exp(x) is an invertible function. Denote V
21
by W.Thus
for any 21/e . y ,N, and in particular for any nonnegative
y, there is a unique value W ( y)ofx for which x exp(x) 5 y.
66. Implicitly differentiate the equation W ( y) exp(W ( y)) 5 y
to show that
W
0
ðyÞ5
1
y 1 exp
WðyÞ
5
WðyÞ
y
1 1 WðyÞ
:
67. Use l’Ho
ˆ
pital’s Rule to show that lim
y-0
WðyÞ=y 5 1:
68. Suppose that 1 , a and 0 , y. Show that W ( y ln(a))/ln(a)
is the unique solution of x a
x
5 y.
69. Show that for any nonnegative number y there is a unique
value of x such that x ln(x) 5 y. Use the Lambert W
function to express the solution as a function of y.
70. Show that for any real number u, there is a unique value
of x such that x 1 ln(x) 5 u. Use the Lambert W function
to express the solution as a function of u.
71. Show that for any real number u, the equation x 1 e
x
5 u has a
unique solution. Verify that x 5 u2W (e
u
) is the solution.
72. Suppose that a and b are constants greater than 1. Deter-
mine where the minimum value of a
x
2log
b
(x) occurs.
73. In this exercise, you will establish an inequality that is
useful in analyzing motion with air resistance.
a. Show that 2 is the minimum value of x 1 1/x for x . 0.
b. Prove that c
t
1 c
2t
. 2ift . 0 and c . 1. Hence,
c
t
2 1 . 1 2 c
2t
if t . 0 and c . 1.
c. Suppose that a and b are positive constants, that c . 1,
and that
Z
a
0
ðc
t
2 1Þdt 5
Z
b
0
ð1 2 c
2t
Þdt:
Show that b . a.
d. Show that if a and b are positive, and if
e
a
2 e
2b
5 a 1 b;
then b . a.
Calculator/Computer Exercises
74. Use the Newton-Raphson Method to find an approxima-
tion to the solution of the equation ln(x) 5 32x. How can
you be sure that there is exactly one real solution?
75. Use the first derivative to minimize
ffiffiffiffiffiffiffiffiffiffiffi
x 2 1
p
=log
3
ðxÞ:
76. Use the first derivative to maximize log
2
(1 1 x
2
)/2
x
,0# x.
77. Find the local extrema of x 1 log
2
(1 1 x 1 x
2
).
78. The integral
R
b
a
1=lnðxÞ
dx approximates the number of
primes p in the interval [a, b]. For example, the 8000
th
and 9000
th
primes are 81799 and 93179 . Thus there
are exactly 1000 primes in the interval [81800, 93179]. The
approximation
R
93179
81800
1=lnðxÞ
dx 5 1000:04::: is quite
good. Using a Riemann sum with N 5 4 and the midpoints
of the subintervals as a choice of points, approximate the
number of primes that lie in the interval [50000, 60000].
(The exact number of primes in the interval is 924.)
5.6 Integration by Substitution
The method of substitution, which is also called “change of variable,” provides a
way to simplify or transform an integrand. We begin by illustrating the method of
substitution with an example.
Consider the integral
Z
cosðx
2
1 1Þ2xdx:
The function φ(x) 5 x
2
1 1 and its derivative φ
0
(x) 5 2x both appear in the inte-
grand. Suppose we denote the expression φ(x) 5 x
2
1 1byu. We write
u 5 x
2
1 1: ð5:6:1Þ
We then have
du
dx
5 2x: It is suggestive to write this as
du
dx
dx 5 2xdx
and to abbreviate this last formula as
du 5 2xdx: ð5:6:2Þ
428 Chapter 5 The Integral

Now we may use equations (5.6.1) and (5.6.2) to rewrite
R
cos ðx
2
1 1Þ2xdx as
R
cosðuÞdu. The transformed integral is considerably simpler. Because an anti-
derivative for cos(u) is sin(u), we have
Z
cos ðuÞdu 5 sinðuÞ1 C:
Rewriting this in term s of the original variable x, we have
Z
cos ðx
2
1 1Þ2xdx5 sinðx
2
1 1Þ1 C:
As with all indefinite integral problems, we can check the answer by differentiation:
d
dx
ðsinðx
2
1 1ÞÞ5 cosðx
2
1 1Þ
d
dx
ðx
2
1 1Þ5 cosðx
2
1 1Þ2x;
as required. To save space, we will not include verifications of our work in later
examples. However, you should get into the habit of checking the antiderivatives
that you obtain.
Let us summarize the method of substitution, which is sometimes referred to as
the u-substitutio n because the vari able that effects the substitution is commonly
designated by u.
Key Steps for the Method of Substitution
1. To apply the method of substitution to an integral of the form
R
f ðxÞdx, find an expression φ(x) in the
integrand that has a derivative φ
0
(x) that also appears in the integrand.
2. Substitute u for φ(x) and du for φ
0
(x)dx.
3. Do not proceed unless the entire integrand is expressed in terms of the new variable u.(No xs can remain.)
4. Evaluate the new integral to obtain an answer expressed in terms of u.
5. Resubstitute to obtain an answer in terms of x.
It is an error to omit step 5. In the example that we worked at the start of this
section, the first four steps result in
Z
cosðx
2
1 1Þ2xdx5
Z
cosðuÞdu 5 sinðuÞ1 C: ð5:6:3Þ
In line (5.6.3), the indefinite integral in the middle is certainly equal to the anti-
derivative on the right. However, these expressions in u are not literally equal to
R
cosðx
2
1 1Þ2xdx, which signifies an antiderivative with respect to x. The anti-
derivative sin(u) 1 C can equal the given integral only after Step 5 has been
performed.
Some Examples
of Indefinite Integration
by Substitution
⁄ EXAMPLE 1 Evaluate the indefinite integral
R
sin
4
ðxÞcosðxÞdx:
Solution We
notice that the expression sin(x), together with its derivative cos(x),
appears in the integrand. This suggests setting
u 5 sinðxÞ and du 5
d
dx
sinðxÞ
dx 5 cosðxÞdx:
5.6 Integration by Substitution 429
The integral then becomes
R
u
4
du, which is readily calculated to be u
5
/5 1 C.
Resubstituting to obtain an expression in x, we conclude that
Z
sin
4
ðxÞcosðxÞdx 5
1
5
sin
5
ðxÞ1 C: ¥
⁄ EXAMPLE 2 Compute the integral
Z
ffiffiffi
x
p
ð21x
3=2
Þ
3
dx:
Solution We
notice that the derivative of the expression (2 1 x
3/2
) is (3/2)x
1/2
and
that the latter is similar (up to a constant multiple) to the numerator. This
motivates the substitution
u 5 2 1 x
3=2
and du 5
d
dx
ð2 1 x
3=2
Þdx 5
3
2
x
1=2
dx:
The formula for du may be rewritten as
ffiffiffi
x
p
dx 5
2
3
du:
Therefore upon sub stitution, our integral becomes
Z
ð2=3Þdu
u
3
5
2
3
Z
u
23
du 5
2
3
2
1
2
u
22
1 C 52
1
3
u
22
1 C:
Resubstituting the x-variable gives
Z
ffiffiffi
x
p
ð21x
3=2
Þ
3
dx 52
1
3
ð21x
3=2
Þ
22
1 C: ¥
The Method of
Substitution for
Definite Integrals
The method of substitution also applies well to definite integrals; the only new
feature is that when we change variables, we must take the limits of integration into
account.
⁄ EX
AMPLE 3 Evaluate the integral
R
4
3
x
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
25 2 x
2
p
dx.
Solution We
observe that the derivative of the expression 25 2 x
2
is 22x. This
motivates the substitution
u 5 25 2 x
2
and du 5
d
dx
ð25 2 x
2
Þdx 522xdx:
However, we must not stop here. In the x-integral, the limits of integration are 3
and 4. When x 5 3, u 5 25 2 3
2
5 16; when x 5 4, u 5 25 2 4
2
5 9. Making our
substitutions, we obtain
Z
4
3
x
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
25 2 x
2
p
dx 52
1
2
Z
4
3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
25 2 x
2
p
ð22xÞdx
52
1
2
Z
9
16
ffiffiffi
u
p
du
430 Chapter 5 The Integral

52
1
2
2
3
u
3=2
u5 9
u5 16
5
2
9
3=2
3
2
2
16
3=2
3
52
27
3
1
64
3
5
37
3
:
INSIGHT
Example 3 demonstrates that a change of variable can convert an integral of
the form
R
b
a
f ðxÞdx with a , b into an integral of the form
R
d
c
gðuÞdu with c . d.Inother
words, a change of variable can reverse the direction of integration. This is perfectly all right.
Calculate in the usual way, and do not omit the minus sign that arises in the calculation of du.
When we apply the method of substitution to a definite integral, it is essential
that we take into account the effect that the change of variables has on the limits of
integration. Example 3 illustrates how to do this while the substitution is being
performed. An alternative method is to calculate the indefinite integral in the
original variable and then use the original limits of inte gration, as is done in the
next example.
⁄ EX
AMPLE 4 Calculate
R
2
0
xe
x
2
dx:
Solution Let
u 5 x
2
and du 5
d
dx
ðx
2
Þdx 5 2xdx:
When x 5 2, we have u 5 2
2
5 4; when x 5 3, we have u 5 3
2
5 9. It follows that
Z
3
2
xe
x
2
dx 5
1
2
Z
9
4
e
u
du 5
1
2
e
u
u5 9
u5 4
5
1
2
ðe
9
2 e
4
Þ:
Alternatively, we can use the method of substitution to calculate an antiderivative
of the given integrand, a procedure that entails resubstitution. Then we use this
antiderivative with the original limits of integrat ion to evaluate the given definite
integral. Thus with u 5 x
2
and du 5 2xdx, we have
Z
xe
x
2
dx 5
1
2
Z
e
u
du 5
1
2
e
u
1 C 5
1
2
e
x
2
1 C:
We may omit the additive constant C when calculating the definite integral. The
result is
Z
3
2
xe
x
2
dx 5
1
2
e
x
2
x5 3
x5 2
5
1
2
ðe
9
2 e
4
Þ;
as we obtained with the first method.
¥
5.6 Integration by Substitution 431

INSIGHT
When evaluating a definite integral by making a substitution, it is
important to use limits of integration that are appropriate for the variable of the inte-
gration. If you resubstitute so that the antiderivative is expressed in terms of the original
variable of integration, then the original limits of integration should be used. If the
antiderivative is expressed in terms of a variable of substitution u, and you do not
resubstitute, then limits of integration must be calculated for u. In general, they will not
be the same as the limits for the original variable, as Example 4 shows.
In the next example, the method of substitution works in a not-so-obvious way.
⁄ EX
AMPLE 5 Evaluate the integral
Z
x
2
ffiffiffiffiffiffiffiffiffiffiffi
x 1 5
p
dx:
Solution We
do not immediately see an expression in the integrand whose
derivative also appears. We instead set u 5 x 1 5 because this substitution simplifies
the radical. It follows that du 5 dx and x 5 u 2 5. The integral now has the form
Z
ðu 2 5Þ
2
ffiffiffi
u
p
du:
If we expand the numerator, this integral becomes
Z
u
2
2 10u 1 25
ffiffiffi
u
p
du 5
Z
ðu
3=2
2 10u
1=2
1 25u
21=2
Þdu 5
2
5
u
5=2
2
20
3
u
3=2
1 50u
1=2
1 C:
Resubstituting the x variable gives a final answer of
Z
x
2
ffiffiffiffiffiffiffiffiffiffiffi
x 1 5
p
dx 5
2
5
ðx15Þ
5=2
2
20
3
ðx15Þ
3=2
1 50ðx15Þ
1=2
1 C: ¥
The Role of the Chain
Rule in the Method
of Substitution
We have not said much about why the method of substitution works. All that the
method really amounts to is an application of the Chain Rule. For instance, sup-
pose that we want to study the integral
Z
FðφðxÞÞ φ
0
ðxÞdx: ð5:6:4Þ
If G is an antiderivative for F, then
ðG
x
φÞ
0
ðxÞ5 G
0
ðφðxÞÞφ
0
ðxÞ5 FðφðxÞÞ φ
0
ðxÞ:
Thus G (φ(x)) is an antiderivative of F (φ(x)) φ
0
(x)and
Z
FðφðxÞÞ φ
0
ðxÞdx 5 GðφðxÞÞ
The method of substitution is merely a device for seeing this procedure more
clearly. We let
u 5 φðxÞ and du 5 φ
0
ðxÞdx
to transform integral (5.6.4) to
Z
FðuÞdu 5 GðuÞ1 C 5 GðφðxÞÞ1 C:
432 Chapter 5 The Integral

When an Integration
Problem Seems to
Have Two Solutions
It is frustrating when your solution to an exercise is different from the solution that
a friend has obtained or from the one in the back of the book. The next example
illustrates how this can happen.
⁄ EX
AMPLE 6 Compute the indefinite integral
Z
sinðxÞcosðxÞdx:
Solution We
use the substitution u 5 sin(x), du 5 cos(x) dx. The integral becomes
Z
sinðxÞcosðxÞdx 5
Z
udu 5
u
2
2
1 C 5
sin
2
ðxÞ
2
1 C:
This problem can be done in several different ways. Another solution can be
derived by setting u 5 cos(x), du 52sin(x) dx. The integral then becomes
Z
sinðxÞcos ðxÞdx 52
Z
udu52
u
2
2
1 C 52
cos
2
ðxÞ
2
1 C:
Although both of these solution methods are correct, the answer sin
2
(x)/2 1 C
appears to be quite different from the answer 2cos
2
(x)/2 1 C. How do we reconcile
this apparent contradiction?
We observe that
sin
2
ðxÞ
2
1 C 5
1 2 cos
2
ðxÞ
2
1 C 52
cos
2
ðxÞ
2
1
1
2
1 C
:
Now the two solutions are starting to look the same. Remember that C is an
arbitrary constant. Hence D 5 1/2 1 C is also an arbitrary constant. Thus we have
discovered that sin
2
(x)/2 1 C is precisely the same solution as 2cos
2
(x)/2 1 D.
In summary, although two methods lead to the same solution, it requires a
trigonometric identity to see that they are the same. Put another way, any two
solutions of our indefinite integral problem will differ by a constant.
¥
Integral Tables Extensive tables of definite and indefinite integrals have been compiled. For more
than 200 years, they have proved to be useful resources for the evaluation of
integrals. Typically, tables of integrals are organized by grouping together inte-
grands that share one or more expressions of the same type. For example, the brief
table of integrals that is found at the back of this text has a section devoted to
integrands that involve sin(x), another section for integrands that involve cos(x),
and an additional section for integrands that involve both sin(x) and cos(x).
An integral formula often can be found in a table of integrals in exactly the
form that is needed. Consider the integral,
R
ðx
2
=
ffiffiffiffiffiffiffiffiffiffiffi
x 1 5
p
Þdx, of Example 5. To
evaluate this integral using the table in this text, we identify the salient expression,
ffiffiffiffiffiffiffiffiffiffiffi
x 1 5
p
, and browse the formulas that involve the term
ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
. We find equation
76, which tells us that
Z
x
2
ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
dx 5
2
b
3
1
5
ða 1 bxÞ
5=2
2
2a
3
ða 1 bxÞ
3=2
1 a
2
ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
1 C:
If we substitute a 5 5 and b 5 1 into this formula, then we obtain
5.6 Integration by Substitution 433

Z
x
2
ffiffiffiffiffiffiffiffiffiffiffi
x 1 5
p
dx 5
2
1
3
1
5
ðx 1 5Þ
5=2
2
2ð5Þ
3
ðx 1 5Þ
3=2
1 5
2
ffiffiffiffiffiffiffiffiffiffiffi
x 1 5
p
1 C;
which agrees with our solution of Example 5.
Sometimes an entry from an integral table is only the first step of a solution.
The next example illustrates this situation.
⁄ EX
AMPLE 7 Use a table of integrals to evaluate
Z
ffiffiffiffiffiffiffiffiffiffiffiffi
5 1 3t
p
ffiffiffiffiffiffiffiffiffiffiffiffi
7 1 4t
p
dt:
Solution Again,
we focus on the term
ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
in the integrand. Equat ion 86,
Z
ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
dx 5
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
1
ða 2 bÞ
ffiffiffi
b
p
ln
ffiffiffiffiffiffiffiffiffiffiffiffiffi
a 1 bx
p
1
ffiffiffi
b
p ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
1 C;
is promising, but we must first do some work to rewrite the given integrand so that
it exactly matches the tabulated form. To that end, we write
ffiffiffiffiffiffiffiffiffiffiffiffi
7 1 4t
p
5 7
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 4t=7
p
,
or
ffiffiffiffiffiffiffiffiffiffiffiffi
7 1 4t
p
5 7
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
for x 5 4t=7. Next, we make the substitution t 5 7x/4, dt 5
(7/4) dx in the original integral:
Z
ffiffiffiffiffiffiffiffiffiffiffiffi
5 1 3t
p
ffiffiffiffiffiffiffiffiffiffiffiffi
7 1 4t
p
dt 5
Z
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5 1 3ð7x=4Þ
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
7 1 4ð7x=4Þ
p
7
4
dx
5
7
4
Z
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5 1 21x= 4
p
ffiffiffi
7
p
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
dx 5
ffiffiffi
7
p
8
Z
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
20 1 21x
p
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
dx:
We may now evaluate the integral on the right by applying equation 86 with a 5 20
and b 5 21. We obtain
ffiffiffi
7
p
8
Z
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
20 1 21x
p
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
dx 5
ffiffiffi
7
p
8
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
20 1 21x
p
2
1
ffiffiffiffiffi
21
p
ln
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
20 1 21x
p
1
ffiffiffiffiffi
21
p ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
1 C:
On resubstituting x 5 4t/7, we find the value of the original integral:
Z
ffiffiffiffiffiffiffiffiffiffiffiffi
51 3t
p
ffiffiffiffiffiffiffiffiffiffiffiffi
71 4t
p
dt 5
ffiffiffi
7
p
8
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
11 4t=7
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
201 21ð4t=7Þ
p
2
1
ffiffiffiffiffi
21
p
ln
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
201 21ð4t=7Þ
p
1
ffiffiffiffiffi
21
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
11 4t=7
p
1 C
5
ffiffiffi
7
p
8
1
ffiffiffi
7
p
ffiffiffiffiffiffiffiffiffiffiffiffi
71 4t
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
201 12t
p
2
1
ffiffiffiffiffi
21
p
ln
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
201 12t
p
1
ffiffiffiffiffi
21
p
ffiffiffi
7
p
ffiffiffiffiffiffiffiffiffiffiffiffi
71 4t
p
1 C
5
1
8
2
ffiffiffiffiffiffiffiffiffiffiffiffi
71 4t
p
ffiffiffiffiffiffiffiffiffiffiffiffi
51 3t
p
2
1
ffiffiffi
3
p
ln
2
ffiffiffiffiffiffiffiffiffiffiffiffi
51 3t
p
1
ffiffiffi
3
p ffiffiffiffiffiffiffiffiffiffiffiffi
71 4t
p
1 C: ¥
434 Chapter 5 The Integral
