Cao Z. (Ed.) Thin Film Growth: Physics, materials science and applications

Подождите немного. Документ загружается.

228

Epitaxial growth of graphene thin films on

single crystal metal surfaces

J. Coraux, Institut Néel, France and a. T. N’DIaye,

C. busse and T. MIChely, universität zu Köln,

Germany

Abstract: epitaxial growth of graphene on metals has been known about

for ve decades and has encountered renewed interest since 2006–2007

when it was realized that graphene mass production is a major hurdle in

the development of graphene-based applications. With the help of model

systems, i.e. prepared in clean conditions (ultra-high vacuum) and at

clean surfaces (single-crystalline metallic ones), much progress has been

made towards the understanding of graphene growth on metals, from

the elementary processes governing growth towards the tailoring of the

morphology of the graphene samples.

Key words: graphene, metals, chemical vapour deposition, defects, structure,

edges, multilayer, growth processes.

10.1 Introduction

Graphene is the name given to an atomically thin layer of sp

-hybridized

carbon (Fig. 10.1). Its unconventional properties were explored by researchers

from 2004, after it was isolated by A. Geim and colleagues. in Manchester

by mechanical exfoliation of graphite (Novoselov, 2004). Such samples

have fuelled exceptionally sustained research owing to their high structural

quality, and they are set to keep revealing a wealth of remarkable properties

resulting from the high surface to volume ratio, mechanical properties,

chemical inertness, electronic band structure, etc., of graphene (Geim, 2009).

a consensus has emerged as to the necessity for alternative preparation

methods, because of large deviations in the quality of samples obtained by

mechanical exfoliation, and because this technique is very fastidious, together

precluding the reliable and efcient production of graphene. Accordingly

alternative preparation methods have been explored, among which are

epitaxial growth on silicon carbide and on metals. In contrast to silicon

carbide, single-crystalline metal substrates can yield high-quality graphene

with one layer uniformly covering a surface (some applications then require

the transfer of graphene onto an adequate support). another direction in

graphene research focuses towards understanding properties, possibly new

ThinFilm-Zexian-10.indd 228 7/1/11 9:42:47 AM



229Epitaxial growth of graphene thin ﬁlms on single crystal metal surfaces

ones, resulting from its interaction with an environment, in particular with a

metal, which has obvious relevance when considering the graphene/electrode

contact. Graphene prepared directly on metal surfaces, which has been known

for decades (Banerjee, 1961; Karu, 1966; Irving, 1967; Presland, 1969),

provides a system ideally suited to address such issues.

Growth processes are often monitored by ne inspection of a system’s

structure. Therefore we rst describe the structure of graphene on metals

including the defects that are commonly encountered. We then focus on the

growth of graphene. Throughout the discussion, we lay emphasis on the

strong inuence of the metal–graphene interaction upon growth processes and

consequently graphene’s structure. based on our studies of graphene growth

on iridium and other contributions in the literature, we review conditions

for obtaining high-quality graphene.

10.2 Structure of graphene on metals

The C–C bond is one of the strongest in nature (3.61 eV for a single bond),

stronger than the bond between carbon and a noble metal. This explains

why sp2 carbon (more stable than sp3) and the noble metal coexist as two

separate phases, at least at room temperature and ambient (or below) pressure.

As we shall discuss in Section 10.3, graphene or multilayer graphene can

Sublattice B

Sublattice A

10.1 Schematics of graphene’s honeycomb structure showing the

two carbon hexagonal sublattices in different shades. The unit cell is

deﬁned by the two lattice vectors represented with black arrows.

ThinFilm-Zexian-10.indd 229 7/1/11 9:42:48 AM



230 Thin ﬁlm growth

be obtained. The epitaxial relationship is more or less well dened: while

the texture orientation is unique ([0001] direction of graphene or graphite

parallel to the dense-packed metal surface normal), the azimuthal (in-plane)

orientation can be multiple, either because different variants can be formed, or

because the azimuthal orientation scatters around an energetically favourable

situation. Graphene is the stiffest material known to date (Lee, 2008), which

has important consequences for its structure: biaxial strains in graphene

resulting from its epitaxial growth are restricted to a few tenths of a percent,

which renders graphene’s lattice incommensurate with that of the substrate in

the general case. Due to the exibility of graphene, delaminations (wrinkles)

are possible in response to thermal mismatch between the substrate and

graphene. Graphene can also bend up or down at substrate edges.

10.2.1 Commensurate or not

among transition metals, Co and Ni dense-packed surfaces exhibit only

small lattice mismatches with graphene, of 1.8 and 1.2% respectively (for

Fe, this is only 0.9%, but presumably due to the large solubility of C in Fe

at ambient conditions, the control of the number of graphene layers on Fe

is almost impossible). Considering graphene’s high young’s modulus (lee,

2008), stretching the graphene to match the metal lattice parameter would,

however, imply that the metal can sustain a considerable amount of stress,

actually more than its breaking strength. This is in apparent contradiction

with experimental observations pointing to a commensurate graphene

layer on the metal. This contradiction may be explained if one considers a

possible change of graphene’s mechanical properties upon its bonding on the

metal (which is strong on Co or Ni). electron diffraction revealed a (1 ¥ 1)

(commensurate) superstructure for graphene/Ni(111). In this superstructure

half the carbon atoms sit on top of the Ni atoms in the topmost substrate

layer, and the remaining carbon atoms sit on top of the Ni atoms in the third

(relative to the topmost Ni layer) substrate layer. The former carbon atoms

are slightly higher than the latter (Gamo, 1997) (Fig. 10.2a).

The situation is more complex in the case of a larger lattice mismatch

between graphene and the substrate. This is the case for a number of transition

metals, like Cu(111) (4% lattice mismatch with graphene), Ir(111), Pt(111),

or Ru(0001) (~10%). With such substrates the coincidence of the graphene

and metal surface lattices can only be local and partial: if at a given location

the centres of carbon rings approximately prolong the fcc(111) or hcp(0001)

atomic arrangement of the metal atoms below, a few nearest neighbour

distances away, this coincidence is lost. This gives rise to a periodic lattice

with the symmetry of the less symmetric surface in the {graphene,metal}

system. In the case of graphene on a metallic surface with hexagonal

symmetry, the superlattice exhibits hexagonal symmetry too. such lattices

ThinFilm-Zexian-10.indd 230 7/1/11 9:42:48 AM



231Epitaxial growth of graphene thin ﬁlms on single crystal metal surfaces

are encountered in various systems, such as metal/metal epitaxial systems

or oxide layers on metals (see, for instance Wiederholt (1995) and ritter

(1998), respectively). Coincidence site lattices are often described following

a moiré pattern (Fig. 10.2b), by analogy with the optical beating fringes

appearing when looking through two thin, transparent, superimposed tissue

veils (historically composed of bres from angora goats, a type of textile

whose name was adapted from arabic to French as ‘moiré’ and to english

as ‘mohair’) with similar bre structure. For convenience and consistency

with the literature, we hereafter use the term ‘moiré’.

Interesting geometric properties are associated with moirés (amidror,

2007). It can be shown that in the case when the metal surface dense-packed

directions align with <11–20> directions in graphene (zigzag directions),

the lattice parameter of the moiré (a

moiré

) can be written in a simple way as

a function of the lattice parameter of the metal (a

) and of graphene (a

1/a

moiré

= 1/a

– 1/a

. This implies that a

moiré

is inversely proportional to

the lattice mismatch between graphene and the metal. For ~ 10% lattice

mismatches between graphene and the metal, a

moiré

is in the range of 2–3 nm,

for graphene on Cu(111), a

moiré

was recently found to be 6.6 nm (Gao, 2010;

Zhao, 2011). Note that the geometrical parameters of the moiré (orientation,

lattice parameter) are very sensitive to faint variations of those of the metal

and of the graphene, which allows a ne description of the graphene or metal

structure (Coraux, 2008; N’Diaye, 2008b, 2009a).

·112

0Ò

|| ·101

Top view

Side view

1st Ni

2nd Ni

3rd Ni

2.11Å 2.16Å

1.96Å

2.09Å

±0.07Å

(a) (b)

10.2 (a) Structural model for graphene on Ni(111) derived from a ﬁt

of I-V LEED spectra (from Gamo, 1997, © Elsevier); (b) ball model for

a moiré between graphene and a Ir(111) plane. Section of zigzag and

armchair carbon rows are highlighted in the bottom left corner.

ThinFilm-Zexian-10.indd 231 7/1/11 9:42:49 AM



232 Thin ﬁlm growth

standard techniques that have been used for identifying graphene’s structure

are surface science ones, most prominently low-energy electron diffraction

(leeD), also scanning tunnelling microscopy (sTM), and to a much lesser

extent reection high-energy electron diffraction (RHEED) or surface X-ray

diffraction (SXRD). As an illustration, Fig. 10.3 shows characteristic signatures

for graphene on lattice mismatched transition metals using leeD, sTM and

rheeD. The leeD pattern displays a sixfold symmetry, appearing as six

groups of spots. The ner structure of these groups reveals two prominent

spots (the outer one for the metal, the inner one for graphene) and satellites

spots that arise from the moiré (N’Diaye, 2008b). STM captures the atomic

structure of graphene (dark spots are centres of carbon rings) modulated by

a larger scale superstructure with a periodicity in the range of 2–3 nm, which

is the moiré pattern (Land, 1992). The RHEED diagrams show sets of crystal

truncation rods whose streaky character point to the atness (except for the

moiré corrugation) of the surface. such patterns are observed periodically

every 60°, in agreement with the sixfold symmetry of the surface. Besides

the zero-order central rod, strong rst-order rods are related to the graphene

(inner) and metal (outer) lattices (see solid arrows in Fig. 10.3c). These

main rods are surrounded by satellite ones, which are related, similar to the

satellite spots in LEED, to the moiré (dotted arrows in the gure).

#1/a

moiré

#1/a

moiré

#1/a

(a)

(b)

(c)

Direct beam

Specular beam

1st moiré

1st graphene

1st lr

2st moiré

1st moiré

0th

11)

(111)

10.3 (a) LEED pattern measured with 80 eV electrons, (b) STM

topographs (left: 8.8 ¥ 8.8 nm

, right: 2.5 ¥ 2.5 nm

), and (c) RHEED

pattern recorded with 10 keV electrons, along the [2

11] azimuth,

for graphene on Ir(111).

(011)

ThinFilm-Zexian-10.indd 232 7/1/11 9:42:50 AM



233Epitaxial growth of graphene thin ﬁlms on single crystal metal surfaces

Finally, note that the above discussion applied to graphene on metal surfaces

with a threefold symmetry. Much less literature addresses graphene prepared

on, for example, (100) surfaces of fcc metals (Hamilton, 1980; Zhao, 2011)

or (110) surfaces of body-centred cubic metals. On these metals graphene/

metal moirés are also found, but their symmetry is decreased compared to

that of moirés with graphene on threefold symmetric surfaces.

10.2.2 Height of the graphene sheet

The distance between the metallic surface and the graphene surface is

characteristic of the metal/graphene interaction. extreme cases for this

interaction are van der Waals binding, such as in between the graphite plane,

and strong hybridization of the metal d bands with the p bands of graphene.

While the rst case mostly preserves the conical character of graphene p

bands, the second deeply modies them, causing band gap opening at the K

point in the brillouin zone and bending of the bands. In both cases, charge

transfer between graphene and the metal is a priori expected.

In the case of dominating van der Waals interactions, as in graphite, the

graphene–metal distance is expected to be close to the graphite interplane

distance, i.e. around 0.345 nm. In the opposite situation, the carbon and

metal atoms form bonds with a covalent character, therefore the distance

is expected to be much shorter (e.g. 0.21 nm for graphene/Ni(111); Gamo,

1997).

The graphene–metal distance remains poorly characterized at experimental

level. This is mainly ascribed to the limitations of the techniques that are

commonly employed: sTM has so far been unable to disentangle topographic

and electronic contributions to the apparent height measurements in the

graphene–metal system (Marchini, 2007; Vazquez de Parga, 2008); atomic

force microscopy (aFM) was only used in air for graphene on metals, so

that the sensitivity of the technique does not allow for a sufciently accurate

determination of the height. The only techniques which proved relevant up to

now are LEED I-V measurements and SXRD which were applied to graphene

on Ni(111), Ru(0001), and Pt(111) (Gamo, 1997a; Martoccia, 2008; Sutter,

2009a; Moritz, 2010). The analysis of the SXRD data relies on the choice

of structural models a priori, which introduces an (unknown) uncertainty

in the value of the graphene–metal height. The LEED I-V analysis is based

on the simulation of electron reectivity using a dynamical diffraction

framework, which allows a partial agreement between the simulations and

the experiment, thus imposing careful interpretation of the simulations.

Concerning theory studies, a number of reports provide estimates of the

graphene–metal distance (Bertoni, 2004; Nemec, 2006, 2008; Giovannetti,

2008; Wang, 2009; Khomyakov, 2009; Ran, 2009). Yet, noticeable deviations

are found, for example for graphene/Pd(111) (Nemec, 2006; Giovannetti,

ThinFilm-Zexian-10.indd 233 7/1/11 9:42:50 AM



234 Thin ﬁlm growth

2008). It can be argued that the geometry used for the calculations is frequently

over-simplied. The approximations employed to perform the ab initio

calculations yield different results: the local density spin approximation is

known to result in overbinding, while the generalized gradient approximation

is expected to result in large graphene–metal distances as suggested by

the over-estimation of the graphene–graphene distance in graphite. Most

important, for a long time van der Waals interactions were not included in

the calculations and are only now starting to be considered (Vanin, 2009;

Lazic, 2010; Busse, 2011).

The difculty in assessing the graphene–metal height also concerns the

modulation of this height in the case of graphene–metal systems with a moiré.

So far, with the exception of one experimental report (Martoccia, 2008),

only demanding rst principle calculations were employed in this respect

(N’Diaye, 2006, 2008a, Feibelman, 2008; Wang, 2008; Brugger, 2009).

From these works it seems that graphene height is modulated between 0.30

and 0.38 nm on Ir(111), a system for which graphene–metal hybridization

is a priori weak (Pletikosic, 2009). On Ru(0001), the height was claimed

to vary between 0.22 and 0.37 nm (Wang, 2008): for the regions where the

height is lower, there is a strong covalent-like graphene–Ru interaction.

10.2.3 Orientation variants, small-angle twins and

dislocations

The epitaxial relationship between graphene and the metal is well dened

along the direction perpendicular to the graphene and metal surface planes:

[0001] for graphite parallel to [111] (fcc metal) or [0001] (hcp metal)

direction. This is not always the case in the plane of the graphene and metal

surfaces, in other words, there exist several preferred azimuthal orientations

for graphene on metal (orientation variants) and the orientation of graphene

may uctuate around these preferred situations. It was recently argued that

the weaker the graphene–metal interaction, the less well dened should the

graphene azimuthal orientation be (Sutter, 2009a).

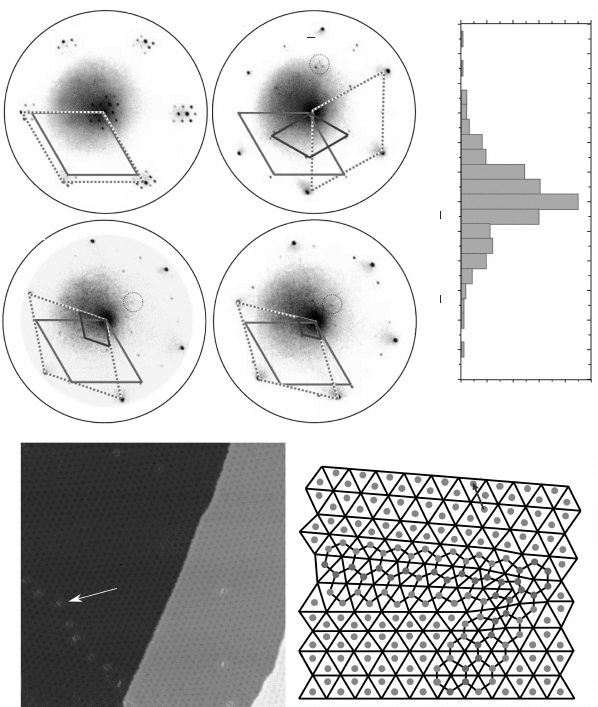
The formation of several orientation variants was highlighted for graphene/

Ir(111) for specic preparation conditions (Loginova, 2009a, 2009b), for

which four orientation variants were identied (Fig. 10.4a). The azimuthal

twin between each variant is large, for several to several tens of degrees.

obviously, each variant represents a local minimum for the total energy

of the graphene–metal system. It seems, however, that the conguration

corresponding to the dense-packed metal rows aligned to the carbon zigzag

edges is more energetically favourable as it always forms rst and can be

exclusively obtained for graphene/Ir(111) in some growth conditions. also

consistent with this larger stability is the fact that this rotation variant is

more inert against oxidation (van Gastel, 2009). Rotational variants were

ThinFilm-Zexian-10.indd 234 7/1/11 9:42:50 AM



235Epitaxial growth of graphene thin ﬁlms on single crystal metal surfaces

(a)

(b)

0° 30°

√ 3

moiré

18.5°

14°

(c)

Domain B

Domain A

0 20 40 60 80 100

Count

–1.2 –1.0 –0.8 –0.6 –0.4 –0.2 0 0.2 0.4 0.6 0.8 1.0 1.2

Angle between ·112

0Ò

and ·101Ò

(°)

10.4 (a) Micro-LEED pattern for each of the four rotational variants

for graphene on Ir(111), corresponding to a rotation of 0°, 30°, 18.5°

and 14° of the carbon zigzag rows with respect to the dense-packed

rows of Ir(111). The dark grey, dotted, and light grey rhombus

highlight the Ir(111), graphene, and moiré unit cells, respectively

prb.aps.org/abstract/PRB/v80/i8/e085430). (b) Distribution of angles

between the graphene zigzag rows (<11-20>) and the dense-packed

rows (<10-1>) of an Ir(111) surface for the energetically preferred

0° rotational variant. (c) (left) STM topograph (108 nm ¥ 108 nm

)

showing three domains with a different orientation of graphene on

Ir(111) and (right) the atomic structure of defects, such as the one

indicated with an arrow on the left panel, which the grain boundaries

Society). Note that the observed superstructure is the graphene/

Ir(111) moiré and that it ampliﬁes small-angle twins. A and B mark

two of the domains; the arrow highlights one of the typical defects

forming the grain boundary.

ThinFilm-Zexian-10.indd 235 7/1/11 9:42:51 AM



236 Thin ﬁlm growth

also found for graphene/Pt(111) (Sasaki, 2000; Sutter, 2009a), but it has

not been possible so far to achieve a single orientation, suggesting that all

variants have comparable stability.

Depending on the growth conditions (see Section 10.3), the azimuthal

orientation of graphene might be more or less well-dened around each

orientation variant (N’Diaye, 2008b). The scatter in this orientations is

characterized by a few tenths of a degree only for graphene/Ir(111) if

graphene is prepared above 1000°C (Fig. 10.4b), and several tens of degrees

if graphene is prepared at 600°C (Coraux, 2008). The smallest scatters can

be efciently characterized by analysing the moiré scatters, which largely

amplify the carbon lattice ones (Coraux, 2008; N’Diaye, 2008a).

at the boundary between graphene domains that are twinned (scattered

twins or orientation variants), the carbon lattice tends to minimize the number

of dangling bonds through the formation of edge dislocations, that is pairs

of a heptagon and a pentagon (Coraux, 2008) as shown in Fig. 10.4(c). Such

defects are known to accommodate twin boundaries (Bollmann, 1964).

10.2.4 Other defects

Deviations from the pure two-dimensional honeycomb structure of graphene

might be considered as defects. a detailed review of defects would include

a discussion of their origin, stability and electronic properties, and is beyond

the scope of this chapter. Defects can be intrinsic to the graphene itself,

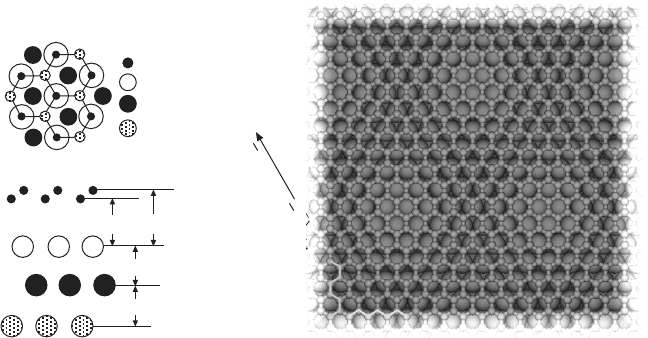
which is the case for vacancies, substitutional atoms, or graphene edges (Fig.

10.5a). They can also be extrinsic, such as being imposed by the graphene

environment, which is the case for graphene undulations induced by those

of the substrate (e.g., step edges) or thermally induced delaminations (Fig.

10.5b). Intrinsic defects for epitaxial graphene are so far poorly characterized.

extrinsic ones are better explored. Graphene wrinkles (linear delaminations)

present after cooling samples down to room temperature following growth

are due to the mismatch of thermal expansion coefcients. The wrinkle

formation actually sets in at a well-dened temperature (whose value depends

on the growth temperature) when cooling samples down (N’Diaye, 2009a),

corresponding to a situation when strain accumulation becomes unfavourable

as compared to a loss of graphene/substrate binding energy and accompanying

bending energy associated with graphene delamination. such defects were

rst investigated for epitaxial graphene on SiC (Cambaz, 2008; Biedermann,

2009; Sun, 2009), and further for graphene on metals (Kim, 2009; Obraztsov,

2007; Chae, 2009; Loginova, 2009a; N’Diaye, 2009a; Sutter, 2009a). Their

nucleation occurs abruptly within a fraction of a second, presumably at

the location of defects in graphene or around substrate step edges where

the graphene lattice is already bent (Chae, 2009). Their propagation is to

the contrary progressive (Sutter, 2009a). The formation of wrinkles (when

ThinFilm-Zexian-10.indd 236 7/1/11 9:42:51 AM



237Epitaxial growth of graphene thin ﬁlms on single crystal metal surfaces

cooling down the sample from growth temperature) and their suppression

(upon heating up the sample again) were shown to take place at distinct

temperatures, pointing to a hysteresis.

The bending of the graphene lattice by the substrate step edges (the

graphene lattice is not interrupted by the step edges) was mainly addressed

for graphene in epitaxy on metals, for both Ru(0001) (Pan, 2007) and Ir(111)

(Coraux, 2008) substrates. The graphene lattice was shown to be continuous

across the substrate step edges. on Ir(111) the radius of curvature could even

be evaluated by taking benet of the graphene/Ir(111) moiré and its high

sensitivity to sub-Ångström displacements. It was found to be close to that

of thinnest single wall carbon nanotubes, i.e. approximately 0.27 nm.

10.3 Growth of graphene on a metal

In discussing graphene growth on metals, one may consider several situations,

rst depending on the nature of the carbon source and the way it is provided,

then depending on the afnity of carbon with the metal substrate. Both

aspects can be linked. For instance, carbon solubility in Ni is of the order

of 1 at% at 1000°C, a temperature which is often used for graphene growth

on Ni, and drastically drops at lower temperature, so that graphene growth

can proceed from segregation of carbon dissolved in bulk Ni, which may be

(a)

(b)

10.5 (a) Vacancies (missing atom in the carbon lattice), substitutional

atoms (replacing a carbon one, shown with a larger radius), and

graphene edges (black: zigzag, grey: armchair); (b) wrinkle formed in

graphene following delamination from the substrate (not shown).

ThinFilm-Zexian-10.indd 237 7/1/11 9:42:52 AM

