Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

321

H C

G C

X Количество

$0x4=0 $0x6=0 $0x1=0 $0x0=0 $0x0=0 $0x120=0

+ + + + + +

$0x2=0 $0x6=0 $0x0=0 $0x1=0 $0x0=0 $0x72=0

+ + + + + +

$0x0=0 $0x1=0 $0x0=0 $0x0=0 $0x1=0 $0x10=0

=$0 Z

=$0

Вычисление

- Z

-Z

=$2-

0=$2

- Z

=$0-0=$0

-Z

=$4-

0=$4

- Z

=$0-0=$0

- Z

=$0-0=$0

Этап 4. Определите, какую переменную следует заменить. В решение

рациональнее ввести переменную G, следующим шагом будет выбор переменной,

подлежащей замене. Для этого разделим каждое значение столбца "Количество" на

соответствующее ему значение в столбце G и выберем переменную, которая даст

наименьшее положительное значение. Именно она и будет замещена.

Для строки S

: 120/6 = 20.

Для строки S

: 72/6 = 12.

Для строки S

: 10/1 = 10.

Поскольку наименьшим значением является 10, нам следует заместить переменную

. В табл. 7д.1 строка для этой переменной помечена маленькой стрелкой,

расположенной в правой части таблицы. Это максимальное значение G, которое может

быть включено в решение. Другими словами, выпуск более чем 10 единиц G превысит

имеющиеся в наличии производственные мощности участка С. Этот результат можно

проверить математически, рассмотрев ограничение G ≤ 10, или визуально, исследовав

графическое отображение задачи, показанное на рис. 7д.1. Из этого графика также видно,

что 20 и 12 — это значения G для двух других ограничений, и если ограничение С ≤ 10

удалить, то в решение можно было бы дополнительно ввести 2 единицы G.

Этап 5. Вычислите новые значения строки для вводимой переменной. Для

введения в решение переменной G требуется замещение всей строки S

. Значения G для

замещения строки получают делением каждого текущего значения S

на значение в

столбце G, соответствующее данной строке. Это значение называют элементом

пересечения (Intersectional Element), поскольку оно находится на пересечении строки и

столбца. Эту перекрестную взаимосвязь выделяют из остальной таблицы, после чего

выполняют все необходимые операции деления, как показано в табл. 7д.З.

Таблица 7д.З. Вычисление новых значений строки для вводимой переменной

0 1 0 0 1 10 0/1 =0, 1/1 =1,0/1 =0,

0/1 =0, 1/1 =1, 10/1 = 10

322

Этап 6. Проверьте остальные строки. Новые значения третьей строки (теперь

относящиеся к переменной G) таковы: 0, 1, 0, 0, 1 и 10. В нашем случае они совпадают со

старыми показателями третьей строки таблицы.

Введение в задачу новой переменной влияет на значения остальных переменных, и

для обновления таблицы необходимо провести второй тур вычислений. В нашем случае

мы хотим определить, как влияет введение переменной G на строки S

и S

. Такие расчеты

выполняются с использованием метода, получившего название метода рычага (Pivot

Method), либо алгебраической подстановкой. Первый метод представляет собой больше

механическую процедуру и широко используется на практике, а второй чаще применяется

для объяснения логики процесса обновления. Процедура использования метода рычага

для получения новых значений S

и S

отображена в табл. 7д.4. (По сути, данный метод

заключается в вычитании умноженных на 6 значений строки 3 из строк S

и S

Коррекция таблицы алгебраической подстановкой заключается в подстановке всего

уравнения для вводимой строки во все остальные строки и решение его для всех

измененных значений переменной каждой строки. Процедура, представленная в табл.

7д.5, показывает, что решение задачи линейного программирования симплексным

методом по сути сводится к решению системы уравнений.

Выделив множители у переменных для новой строки S

из табл. 7д.5, получаем такие

же значения, как и при использования метода рычага: 4, 0, 1, 0, –6, 60.

Результаты вычислений на этапах с третьего по шестой вместе с вычислениями Z

— Z

отображены в табл. 7д.6. Воспользовавшись терминологией, принятой в

математическом программировании, можно сказать, что мы закончили первую итерацию

поиска решения задачи.

Оценивая полученное решение, следует обратить особое внимание на два момента:

прибыль составляет 40 долл., но важнее то, что возможно дальнейшее улучшение этого

показателя, поскольку в строке С

—Z

мы имеем положительное значение.

Вторая итерация. Поскольку переменная Н имеет наибольший показатель C

— Z

2, она и будет вводиться. Заменяемой переменной будет S

, так как при делении значений

из столбца "Количество" на соответствующие им значения из столбца Н она получит

наименьшее значение:

= 60/4 = 14; S

= 12/2 = 6; S

= 10/0 = ∞.

Таким образом, в строку Я будут введены следующие значения:

2/2=1, 0/2 = 0, 0/2 = 0, 1/2 = 1/2, -6/2 = -3, 12/2 = 6.

Откорректированная в табл. 7д.7 строка S

0, 0, 1, -2, 6, 36.

Откорректированная в табл. 7д.7 строка С:

0, 1,0,0, 1, 10.

Воспользовавшись результатами табл. 7д.7, построим третью табл. 7д.8.

Анализируя табл. 7д.8, мы видим, что, введя максимальное значение S

(что

технически вполне осуществимо), можно достичь дальнейшего улучшения. Из расчетов в

нижней части табл. 7д.8 получаем, что вследствие ограничения по показателю S

максимальное значение S

, которое можно будет ввести в решение, составляет шесть

единиц. Заменив показатель S

показателем S

и проведя корректировку, составляем табл.

7д.9.

Поскольку строка Cj — Zj содержит только отрицательные значения, дальнейшее

улучшение невозможно, следовательно, в результате трех итераций мы достигли

оптимального решения (Н = 24, G = 4). Во врезке "Краткое изложение этапов

симплексного метода: задача на максимизацию прибыли" вашему вниманию представлено

краткое изложение всех пройденных нами этапов.

Задача минимизации затрат. В примере с компанией Риск and Pawn мы имели

дело с задачей максимизации. Процедура, выполняемая при решении задач

323

минимизации, практически идентична. Различие заключается лишь в том, что ставится

противоположная цель и потенциальное улучшение отображается отрицательным

значением С

— Z

. Следовательно, вначале в решение будет вводиться переменная с

наибольшим отрицательным значением столбец для этой переменной помечен маленькой

стрелкой, расположенной под ним. (Для достижения каждого улучшенного решения

одновременно можно добавлять только одну переменную.)

— Z

. Однако при решении задачи данного вида необходимо ввести

дополнительные переменные, так как задачи минимизации включают с себя ограничения

типа "больше или равно", которые должны обрабатываться иначе, чем ограничения

"меньше или равно", характерные для задач максимизации. К особенностям

использования ограничений типа "больше или равно" и "меньше или равно" мы еще

вернемся в этом дополнении к главе.

Таблица 7д.4. Метод рычага

Старая

строка

Элемент

пересечени

я старой

строки S1

Соответствующий

элемент новой

строки G

Обновленна

я строка S1

Старая

строка

Элемент

пересечени

я старой

строки S2

Соответст

вующий

элемент

новой

строки G

Обновленна

я строка S2

4 - (6 X 0) = 4 2 - (6 X 0) = 2

6 - (6 X 1) = 0 6 - (6 X 1) = 0

1 - (6 X 0) = 1 0 - (6 X 0) = 0

0 - (6 X 0) = 0 1 - (6 X 0) = 1

0 - (6 X 1) = -6 0 - (6 X 1) = -6

120 - (6 10) = 60 72 - (6 X 10) = 12

Таблица 7д.5. Алгебраическая подстановка

Нахождение новых значений для S

1. Запишите исходную строку для S

с добавленными к ней свободными переменными (из

первой таблицы):

4H + 6G + 1S, + 0S

+ 0S

= 120.

2. Запишите вводимую строку как ограничение с добавленными свободными переменными

(это значения, вычисленные в табл. 7д.З):

0H+G + 0S

+ 0S

+1S

= 10.

3. Перестройте вводимую строку с учетом вводимой переменной G:

10 -S

4. Подставьте (10 - S

) для переменной G в первое уравнение (старая строка для S

) и

решите полученное уравнение для каждого коэффициента переменной:

4Н + 6(10- S

) + 1S

, = 120

4H + 60-6S

+1S

= 120

4H+1S

-6S

= 120-60

4Н + 1S

- 6S

= 60

или

4Н + 0G + 1S

+ 0S

- 6S

= 60.

Таблица 7д.6. Вторая таблица для задачи о производстве хоккейных клюшек и шахматных

наборов

Сj

Совокупное

$2 S4 $0 $0 $0

Количество

324

решение

Н G

4 0 1 0 -6 60

2 0 0 1 -6 12<-

0 1 0 0 1 10

$0 $0

$40

Cj-Zj

$0 $0 $0 $-4

Этап 4. Определите, какую переменную следует заменить. В решение

рациональнее ввести переменную G, следующим шагом будет выбор переменной,

подлежащей замене. Для этого разделим каждое значение столбца "Количество" на

соответствующее ему значение в столбце G и выберем переменную, которая даст

наименьшее положительное значение. Именно она и будет замещена.

Для строки S

: 120/6 = 20.

Для строки S

: 72/6 = 12.

Для строки S

: 10/1 = 10.

Поскольку наименьшим значением является 10, нам следует заместить переменную

. В табл. 7д.1 строка для этой переменной помечена маленькой стрелкой,

расположенной в правой части таблицы. Это максимальное значение G, которое может

быть включено в решение. Другими словами, выпуск более чем 10 единиц G превысит

имеющиеся в наличии производственные мощности участка С. Этот результат можно

проверить математически, рассмотрев ограничение G ≤ 10, или визуально, исследовав

графическое отображение задачи, показанное на рис. 7д.1. Из этого графика также видно,

что 20 и 12 — это значения G для двух других ограничений, и если ограничение G ≤ 10

удалить, то в решение можно было бы дополнительно ввести 2 единицы G.

Этап 5. Вычислите новые значения строки для вводимой переменной. Для

введения в решение переменной G требуется замещение всей строки S

. Значения G для

замещения строки получают делением каждого текущего значения 5, на значение в

столбце G, соответствующее данной строке. Это значение называют элементом

пересечения (Intersectional Element), поскольку оно находится на пересечении строки и

столбца. Эту перекрестную взаимосвязь выделяют из остальной таблицы, после чего

выполняют все необходимые операции деления, как показано в табл. 7д.З.

Таблица 7д.З. Вычисление новых значений строки для вводимой переменной

0 1 0 0 1 10 0/1 =0, 1/1 =1,0/1 =0,

0/1 =0, 1/1 =1, 10/1 = 10

Этап 6. Проверьте остальные строки. Новые значения третьей строки (теперь

относящиеся к переменной G) таковы: 0, 1, 0, 0, 1 и 10. В нашем случае они совпадают со

старыми показателями третьей строки таблицы.

Введение в задачу новой переменной влияет на значения остальных переменных, и

для обновления таблицы необходимо провести второй тур вычислений. В нашем случае

мы хотим определить, как влияет введение переменной G на строки S

и S

. Такие расчеты

выполняются с исполь-

зованием метода, получившего название метода рычага (Pivot Method), либо

325

алгебраической подстановкой. Первый метод представляет собой больше механическую

процедуру и широко используется на практике, а второй чаще применяется для

объяснения логики процесса обновления. Процедура использования метода рычага для

получения новых значений S

и S

отображена в табл. 7д.4. (По сути, данный метод

заключается в вычитании умноженных на 6 значений строки 3 из строк S

и S

Коррекция таблицы алгебраической подстановкой заключается в подстановке всего

уравнения для вводимой строки во все остальные строки и решение его для всех

измененных значений переменной каждой строки. Процедура, представленная в табл.

7д.5, показывает, что решение задачи линейного программирования симплексным

методом по сути сводится к решению системы уравнений.

Выделив множители у переменных для новой строки S

из табл. 7д.5, получаем такие

же значения, как и при использования метода рычага: 4, 0, 1, 0, —6, 60.

Результаты вычислений на этапах с третьего по шестой вместе с вычислениями Zj и

— Z

отображены в табл. 7д.6. Воспользовавшись терминологией, принятой в

математическом программировании, можно сказать, что мы закончили первую итерацию

поиска решения задачи.

Оценивая полученное решение, следует обратить особое внимание на два момента:

прибыль составляет 40 долл., но важнее то, что возможно дальнейшее улучшение этого

показателя, поскольку в строке C

—Z

мы имеем положительное значение.

Вторая итерация. Поскольку переменная Н имеет наибольший показатель C

—

2, она и будет вводиться. Заменяемой переменной будет S

, так как при делении значений

из столбца "Количество" на соответствующие им значения из столбца Н она получит

наименьшее значение:

= 60/4 = 14;

= 12/2 = 6;

= 10/0 = &.

Таким образом, в строку Н будут введены следующие значения:

2/2=1, 0/2 = 0, 0/2 = 0, 1/2 = 1/2, -6/2 = -3, 12/2 = 6.

Откорректированная в табл. 7д.7 строка S

0, 0, 1, -2, 6, 36.

Откорректированная в табл. 7д.7 строка G:

0, 1, 0, 0, 1, 10.

Воспользовавшись результатами табл. 7д.7, построим третью табл. 7д.8.

Анализируя табл. 7д.8, мы видим, что, введя максимальное значение S

(что

технически вполне осуществимо), можно достичь дальнейшего улучшения. Из расчетов в

нижней части табл. 7д.8 получаем, что вследствие ограничения по показателю S

максимальное значение S

, которое можно будет ввести в решение, составляет шесть

единиц. Заменив показатель S

показателем S

и проведя корректировку, составляем табл.

7д.9.

Поскольку строка Cj — Zj содержит только отрицательные значения, дальнейшее

улучшение невозможно, следовательно, в результате трех итераций мы достигли

оптимального решения (Н— 24, G= 4). Во врезке "Краткое изложение этапов

симплексного метода: задача на максимизацию прибыли" вашему вниманию представлено

краткое изложение всех пройденных нами этапов.

Задача минимизации затрат. В примере с компанией Риск and Pawn мы имели

дело с задачей максимизации. Процедура, выполняемая при решении задач

минимизации, практически идентична. Различие заключается лишь в том, что ставится

противоположная цель и потенциальное улучшение отображается отрицательным

значением Сj — Zj Следовательно, вначале в решение будет вводиться переменная с

наибольшим отрицательным значением

Cj — Zj. Однако при решении задачи данного вида необходимо ввести

дополнительные переменные, так как задачи минимизации включают с себя ограничения

326

типа "больше или равно", которые должны обрабатываться иначе, чем ограничения

"меньше или равно", характерные для задач максимизации. К особенностям

использования ограничений типа "больше или равно" и "меньше или равно" мы еще

вернемся в этом дополнении к главе.

Таблица 7д.4. Метод рычага

Старая

строка

Элемент

пересечения

старой

строки S,

Соответству

ющий

элемент

новой

ст

оки G

Обновленн

ая строка

Старая

строка

Элемент

пересечения

старой

строки S2

Соответству

ющий

элемент

новой

ст

оки G

Обновле

нная

строка

4 - (6 X 0) = 4 2 - (6 X 0) = 2

6 - (6 X 1) = 0 6 - (6 X 1) = 0

1 - (6 X 0) = 1 0 - (6 X 0) = 0

0 - (6 X 0) = 0 1 - (6 X 0) = 1

0 - (6 X 1) = -6 0 - (6 X 1) = -6

120 - (6 10) = 60 72 - (6 X 10) = 12

Таблица 7д.5. Алгебраическая подстановка

Нахождение новых значений для S

1. Запишите исходную строку для S

с добавленными к ней свободными переменными (из

первой таблицы):

4H + 6G+1S

+ 0S

= 120.

2. Запишите вводимую строку как ограничение с добавленными свободными

переменными (это значения, вычисленные в табл. 7д.З):

0H+G + 0S

+ 0S

+1S

=10.

3. Перестройте вводимую строку с учетом вводимой переменной G:

10-S

4. Подставьте (10 - Sз) для переменной G в первое уравнение (старая строка для S

) и

решите полученное уравнение для каждого коэффициента переменной:

4Н + 6(10- S

) + 1S

= 120

4Н + 60-6S

+1S

= 120

4H+1S

-6S

= 120-60

4Н + 1S

- 6S3 = 60

или

4H + 0G + 1S

+ 0S

-6S

= 60.

Таблица 7д.6. Вторая таблица для задачи о производстве хоккейных клюшек и шахматных

наборов

Совокупное

решение

$2 S4 $0 $0 $0

Н G S1 s2 s3

Количество

$0 S1 4 0 1 0 -6 60

$0 S2 2 0 0 1 -6 12←

$4 G 0 1 0 0 1 10

Zj $0 $4 $0 $0 $4 $40

327

Cj-Zj

$0 $0 $0 $-4

Таблица 7д.7. Корректировка строк S

и G

Старая

строка

Элемент

пересечения

старой

Соответств

ющий

элемент новой

строки Н

Новая

строка

Старая

строка

Элемент

пересечения

старой

Соответств

ющий

элемент новой

строки Н

Обновленная

строка G

4 - (4 X 1) = 0 0 - (0 X 1) = 0

0 - (4 X 0) = 0 1 - (0 X 0) = 1

1 - (4 X 0) = 1 0 - (0 X 0) = 0

0 - (4 X 1/2) = -2 0 - (0 X 1/2) = 0

-6 - (4 X -3) = 6 1 - (0 X -3) = 1

60 - (4 6) = 36 10 - (0 X 6) = 10

Таблица 7д.8. Третья таблица для задачи о производстве хоккейных клюшек и шахматных

наборов

Совокупное

решение

$2 $4 $0 $0 $0

Сj

Н G S

Количество

0 0 1

-2

6 36←

1 0 0 1/2 -3 6

0 1 0 0 1 10

$2 $4 $0 $1 $-2 $52

Cj-Zj

$0 $0 $0 $-1

36/6 = 6 6/-3 = -2 (отрицательное значение) 10/1 = 10

Поскольку в данной задаче три уравнения ограничений, в решении должно быть три

переменные с неотрицательными значениями и отрицательное значение нельзя вводить в решение.

Таблица 7д.9. Четвертая таблица для задачи о производстве хоккейных клюшек и

шахматных наборов (оптимальное решение)

$2 54 $0 $0 $0

Сj

Совокупное

решение

Н G S

Количество

$0 S3 0 0 1/6 -1/3 1 6

$2 н 1 0 1/2 -1/2 0 24

$4 G 0 1 -1/6 1/3 0 4

Zj $2 $4 $1/3 $1/3 $0 $64

Cj-Zj

$0 $-1/3 $-1/3 $0

Определение пути поиска решения при симплексном методе

Как уже отмечалось выше, оптимальное решение для задач линейного

328

программирования получают нахождением экстремальной угловой точки. Симплексная

процедура начинается с получения исходного решения, за которым следует поиск

следующего наиболее выгодного и "перескакивание с одной точки пересечения прямых на

другую (или, в случае с многомерным пространством, от одного пересечения плоскостей

на другое). Оценка угловой точки выполняется в результате одной итерации, и, достигнув

наиболее удаленной точки (в случае с задачами на максимизацию прибыли на этапе, когда

следующая за ней точка отображает снижение прибыли), вы получаете оптимальное

решение.

Краткое изложение этапов симплексного метода: задача на максимизацию прибыли

1. Сформулируйте задачу: определите целевую функцию и наметьте ограничения.

2. Постройте исходную таблицу со свободными переменными в совокупном решении и

вычислите строки Zj и Cj — Zj.

3. Определите, какую переменную следует ввести в решение (наибольшее значение Сj — Zj).

4. Определите, какую переменную следует заменить (по наименьшему положительному

коэффициенту, получаемому делением значений столбца "Количество" на соответствующее ему

значение из столбца, выбранного на этапе 3).

5. Вычислите новые значения строки для ввода переменной и вставьте в таблицу новую

строку (строка, подлежащая замене, плюс элемент пересечения).

6. Откорректируйте остальные строки и введите их в новую таблицу; вычислите новые

значения для строк Zj и Cj — Zj (показатели исходных строк, минус элемент пересечения из

исходной строки, умноженный на соответствующий ему элемент из новой строки). Если в

результате вы не получаете ни одного положительного значения Сj — Zj, значит, данное решение

будет оптимальным. Если же такое значение есть, повторите этапы с 3 по 6.

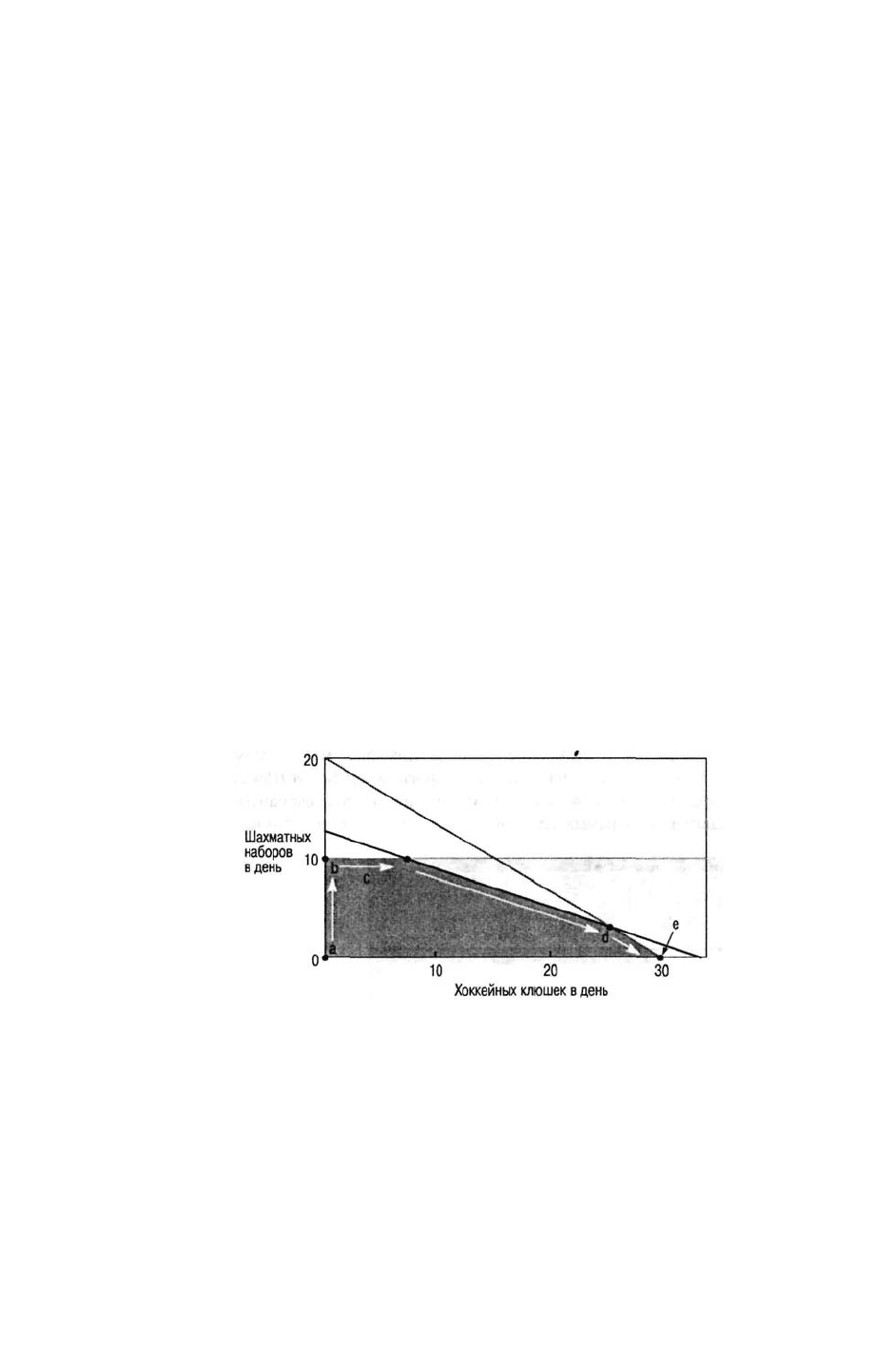
Обратимся к графику на рис. 7д.2, составленному для обсуждаемого нами примера

поиска решения симплексным методом, начиная с исходной точки а (прибыль равна

нулю).

Рис. 7д.2. График последовательности оценки угловых точек для задачи о производстве хоккейных

клюшек и шахматных наборов

В ходе первой итерации в точке b было введено 10 единиц С (прибыль составила

$40). В ходе второй итерации в точке с было введено 6 единиц Н (прибыль составила $52).

Третья итерация привела задачу к окончательному оптимальному решению в точке d

(прибыль составила $64). Обратите внимание, что в ходе этой процедуры мы не

вычисляли показатели прибыли для всех точек, имеющихся в задаче. Если же это сделать

и заглянуть дальше — на основе вычислений C

— Z

чтобы узнать, возможно ли

дальнейшее улучшение в результате перемещения в точку с, то мы убедимся, что данное

изменение уже не приведет ни к каким улучшениям. Эти две характеристики — оценка

угловых точек и оценка дальнейших возможностей улучшений — и составляют основу

симплексного метода.

329

Еще одно свойство симплексного метода состоит в том, что в нем не предусмотрено

достижение оптимальной точки по кратчайшему маршруту вокруг допустимой области.

На графике видно, что если бы процедура решения следовала по пути а→е→d,

оптимальное решение можно было бы получить в результате всего двух, а не трех

итераций.

Мы не следовали этим маршрутом потому, что прибыль на один шахматный набор

была выше прибыли на одну клюшку, вследствие чего симплексный метод указал, что в

ходе первой итерации следует вводить не переменную Н, а переменную G, что в свою

очередь определило направление последующих итераций к точкам c и d. Обратите

внимание: в силу того, что пространство решения имеет форму выпуклого

многоугольника (как говорилось раньше), прибыль не может повыситься, понизиться и

затем опять повыситься.

Анализ чувствительности решения и теневые цены

Внимательно анализируя последнюю (оптимальную) симплексную таблицу (см.

табл. 7д.9), можно получить немало дополнительных сведений. Кроме конкретного

решения, она предоставляет ценную информацию об использовании ресурсов, об

интервале, в котором оптимальное решение остается неизменным, а также об интервале, в

котором коэффициенты целевой функции не изменяют оптимального решения. В

частности, она позволяет ответить на такие вопросы: следует ли вашей фирме приобретать

дополнительные ресурсы? Если — да, то какую цену вы готовы заплатить? Сколько

единиц ресурсов следует приобрести по этой цене? Подобные вопросы можно задавать и

относительно продажи ресурсов: даже если данный ресурс используется в настоящее

время для выпуска продукции фирмы, не будет ли выгоднее отказаться от дальнейшего

производства и продать его по определенной цене? Находить правильные ответы на такие

вопросы очень важно, и симплексный метод позволяет это делать. Причем эти ответы

дополняют оптимальное решение, вычисленное в соответствии с целевой функцией в

табл. 7д.9.

Кроме перечисленных выше вопросов, можно задать и такой вопрос: если мы

изменим прибыль на единицу продукции (изменив коэффициент целевой функции), не

приведет ли это к изменению оптимального решения? Отыскивая на него ответ, мы имеем

дело с анализом чувствительности (Sensitivity Analysis), который заключается в

определении того, насколько изменится решение в результате некоторых изменений

целевой функции, или наоборот, как изменение решения повлияет на целевую функцию.

Вернемся к табл. 7д.9. Значения C

— Z

, связанные со свободными переменными,

называют теневыми ценами (Shadow Prices), безубыточными ценами, предельными

значениями или приростными значениями. Обратите внимание, теневые цены для S

и S

составляли $1/3 (или 33 цента) каждая, а для S

— $0. При любом превышении этой цены

управленческий персонал будет стремиться к продаже ресурсов, а при понижении ниже

этого уровня — приобрести их. А теперь предлагаем вам еще раз рассмотреть, как

решается эта задача, на этот раз с применением доступной компьютерной техники.

Решение задач линейного программирования в MS Excel

Для решения задач линейного программирования часто используются электронные

таблицы. В большинство таких таблиц встроены понятные и простые в применении

стандартные программы. В программе Microsoft Excel, например, есть оптимизирующий

инструмент Solver (Поиск решения), работу которого мы продемонстрируем опять же для

решения задачи о производстве хоккейных клюшек и шахмат. Программа Solver (Поиск

330

решения) запускается из меню Tools (Сервис), после чего появляется диалоговое окно,

запрашивающее информацию, необходимую для ее работы.

Вначале нужно поставить задачу, указав целевую ячейку (или целевую функцию),

изменяемые ячейки (искомые переменные) и ячейки ограничений. На рис. 7д.З

изображена электронная таблица с информацией, которая необходима для решения

данной задачи.

Поле Target Cell (Установить целевую ячейку) (в нашем случае ячейка D5) содержит

формулу, умножающую количество произведенных клюшек и шахматных наборов на

соответствующую им прибыль; значения, указанные в поле Changing Cells (Изменяя

ячейки), соответствуют искомым переменным задачи. В поле Subject to Constraints

(Ограничения) указаны ячейки для введения конкретных ограничений на решение.

Обратите внимание, что в диалоговом окне Solver (Поиск решения) необходимо указать,

что наши значения для решения должны быть больше или равны нулю.

На рис. 7д.З не показано диалоговое окно Options (Параметры), но если его вывести

на экран, то появится поле, в котором можно указать, что данная задача является

линейной, что позволяет значительно ускорить процесс ее решения. В этом окне, которое

управляет механизмом поиска решения используемым программой Solver (Поиск

решения), можно выбрать и многие другие варианты. Данная программа способна решать

задачи с использованием различных стратегий поиска, отличных от симплексного метода.

Рис. 7д. 3. Поиск решения задачи (Solver) в программе Microsoft Excel

После введения информации в это диалоговое окно можно нажать кнопку Solve

(Выполнить) и решить задачу. При этом мы получим несколько разных отчетов. Наиболее

интересными отчетами для нашей задачи являются Answer Report (Отчет по результатам)

и Sensitivity Report (Отчет по устойчивости), примеры которых приведены на рис. 7д.4.

Answer Report (Отчет по результатам) включает окончательные ответы по общей

прибыли (64 долл.) и по количествам производимой продукции (24 хоккейные клюшки и 4

шахматных набора). В разделе Constraints (Ограничения) этого отчета отображено

состояние каждого ресурса, из которого видно, что компанией будут загружены все