Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент
Подождите немного. Документ загружается.


331
станки участков А и В, а станки участка С простоят 6 часов.
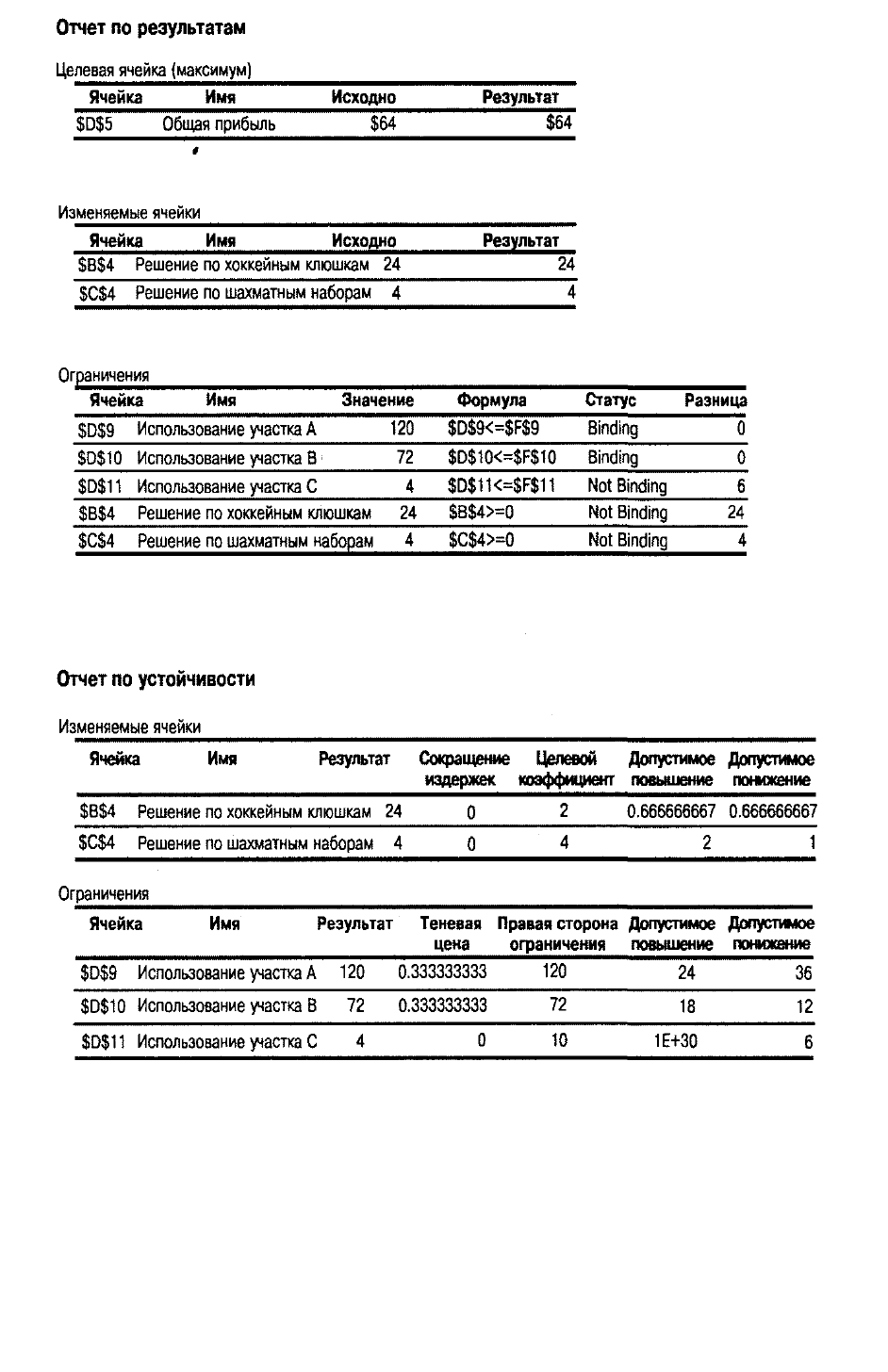
Sensitivity Report (Отчет по устойчивости) делится на две части. Первая часть
озаглавлена "Изменяемые ячейки" и соответствует коэффициентам целевой функции.
Прибыль на единицу продукции для клюшек может увеличиться либо уменьшиться на
0,67 долл. (т.е. может находиться между 2,67 и 1,33 долл.), не оказывая при этом влияния
на решение. Точно так же прибыль на единицу шахматных наборов может быть между 6 и
3 долл., и решение при этом также не изменится. В случае с участком А ограничение
увеличится до 144 (120 + 24) или уменьшится до 84 единиц, что даст в результате
повышение либо снижение целевой функции на 0,33 долл. соответственно. Ограничение
для участка В увеличится до 90 единиц или уменьшится до 60 с тем же изменением
целевой функции в 0,33 долл.
Что касается участка С, то ограничение может увеличиваться до бесконечности (IE +
30 — это на рис. 7д.4 мудреная запись очень большого числа, принятая в Excel) или
уменьшиться на 4 единицы, не изменяя при этом целевую функцию.
Транспортный метод
Транспортный метод (Transportation Method) представляет собой упрощенный
специфический вариант симплексного метода. Он получил такое название потому, что
широко применяется для решения задач, связанных с транспортировкой продукции из
разных источников в несколько пунктов назначения. Задачи такого типа обычно
преследуют одну из двух возможных целей: минимизация затрат по доставке n-го
количества единиц продукции в m-е число пунктов назначения и максимизация прибыли
от транспортировки n-ro количества единиц продукции в т пунктов назначения. Решение
транспортных задач, как правило, выполняется в три стадии, которые мы обсудим на
простом примере.
332
Рис. 7д.4. Отчеты Microsoft Excel Solver
Предположим, компания Риск and Pawn владеет четырьмя фабриками, продукция с
которых поступает на четыре склада, и управленческий персонал хочет составить график
доставки шахматных наборов с минимальными затратами на основе показателей
ежемесячного объема выпускаемой продукции. Объем поставок фабрик, потребности
складов и издержки по транспортировке каждой упаковки шахмат отображены в табл.
7д.10.
Стадия I. Построение транспортной матрицы
333
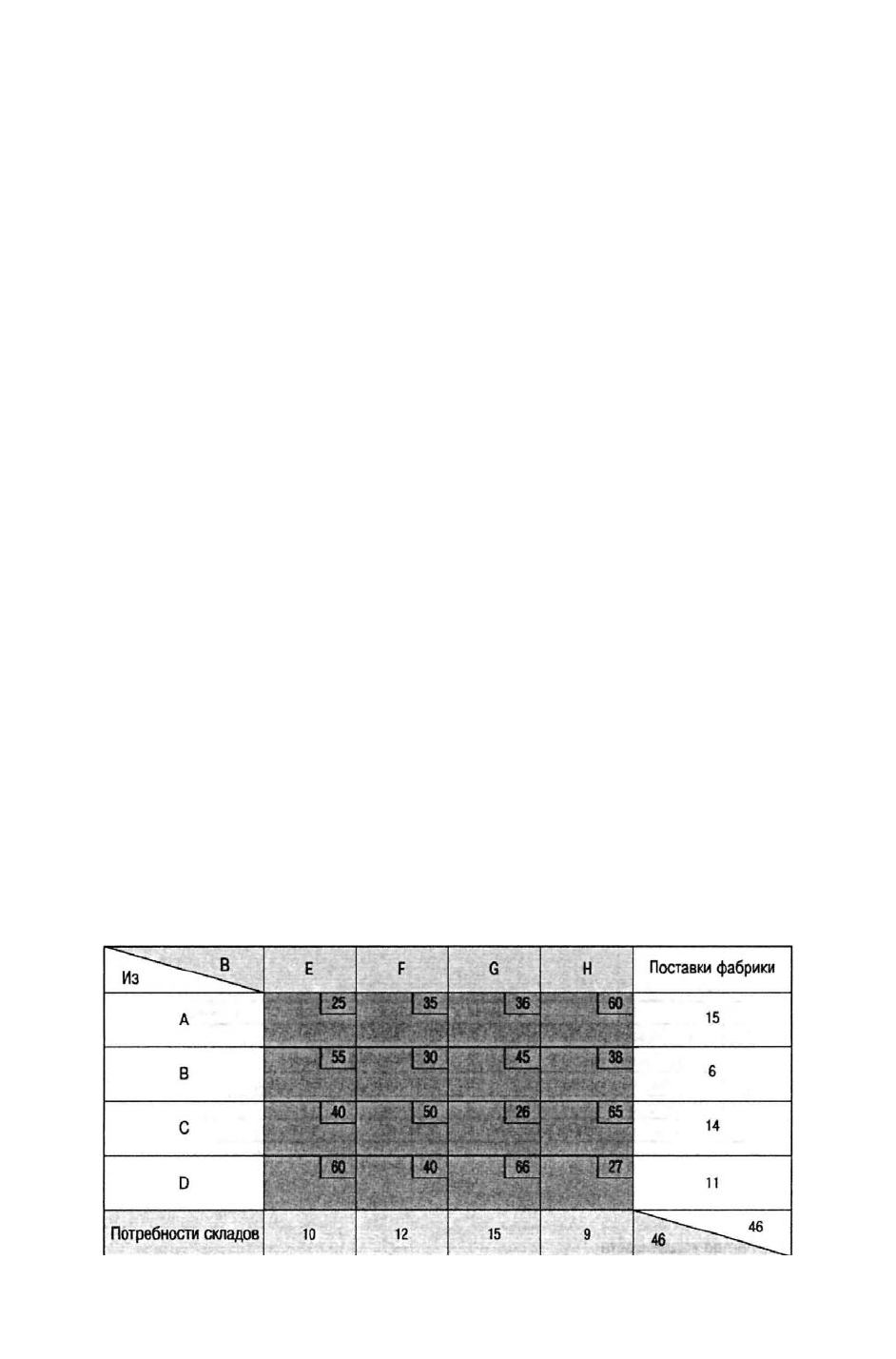
Транспортная матрица для нашего примера изображена на рис. 7д.5.
В крайнем правом столбце отображаются объемы поставок каждой фабрики, а в
нижней строке — потребности каждого склада. Затраты на транспортировку единицы
продукции указаны в маленьких прямоугольниках в каждой ячейке. На этом этапе важно
убедиться, что общие объемы поставок совпадают с общими потребностями. В нашем
примере оба этих показателя равны 46 единицам, однако нередки ситуации, когда один из
них превышает другой. В таких случаях для того, чтобы применить транспортный метод,
в задачу включают фиктивный склад или фабрику. Эта процедура заключается во вставке
дополнительной строки (для добавления фабрики) или еще одного столбца (для
добавления склада). Объем поставок или потребности дополнительного фиктивного
склада или фабрики — это разница между суммарными показателями строк и столбцов.
Так, например, изменим условия рассматриваемой нами задачи и укажем общую
потребность в продукции в размере 36 единиц. В этом случае нам придется добавить в
таблицу новый столбец, в котором указывается потребность фиктивного склада в размере
10 единиц, что в результате даст необходимые 46 наборов. Показатели затрат в каждой
ячейке фиктивной строки будут в этом случае нулевыми, т.е. отправленные сюда единицы
не дают никаких издержек на транспортировку. Теоретически данная корректировка
является эквивалентом симплексной процедуры вставки в неравенства ограничений
свободной переменной с тем, чтобы преобразовать его в уравнение, и, так же как при
симплексном методе, затраты фиктивного подразделения представляются в целевой
функции с нулевым значением.
Данную задачу также можно решить с помощью компьютерной программы
Microsoft Excel. На рис. 7д.6 показано, как нужно поставить задачу в MS Excel. Строки
1—6 используются для указания затрат, поставок фабрик и потребностей складов.
Решение (Changing cells, Изменяемые ячейки) выводится в диапазоне ячеек В8—Е11.
Затраты вычисляются в строках 15—19. Общие затраты указаны в ячейке F19. В
следующем разделе мы продолжим описание способа решения данной задачи без
применения компьютерной техники.
Стадия II. Исходное распределение
Исходное распределение осуществляется размещением данных по ячейкам матрицы
в соответствии с ограничениями на поставки и потребности в продукции. Мы обсудим
несколько методов выполнения этой операции: метод северо-западной ячейки, метод
наименьших затрат и метод приближений Фогеля.
Рис. 7д.5. Транспортная матрица для задачи транспортировки шахматных наборов
Таблица 7д.10. Данные для задачи транспортировки шахматных наборов

334
Затраты на транспортировку единицы продукции (в долл.)
Фабрика
Объем
поставок
Склад Потребность С фабрики
На склад
Е
На склад
F
На склад
G
На склад
Н
А 15 E 10 А 25 35 36 60
В 6 F" 12 В 55 30 45 38
С 14 G 15 С 40 50 26 65
D 11 Н 9 D 60 40 66 27
Рис. 7д. 6. Решение транспортной задачи с помощью программы MS Excel
Распределение методом северо-западной ячейки
Метод северо-западной ячейки, как следует из его названия, состоит в том, что
распределение начинается с верхнего левого угла матрицы и в ячейках первой строки
указываются как можно большие значения
4
. Затем данная процедура повторяется для
второй, третьей строки и т.д., пока все потребности не будут распределены по строкам и
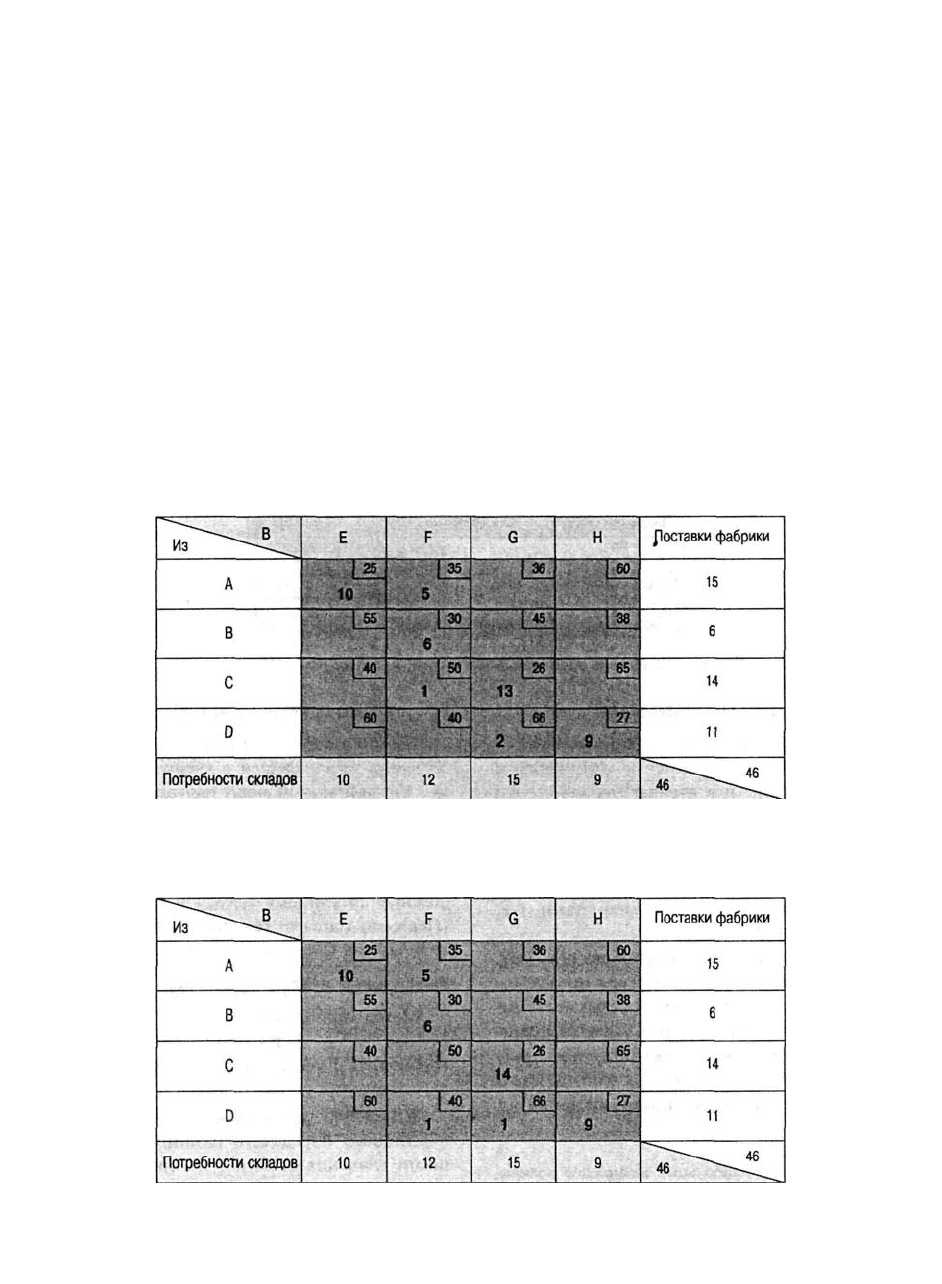
столбцам. На рис. 7д.7 показан пример такого распределения. (Первой заполняется ячейка
с координатами А-Е, второй — A-F, третьей — B-F и т.д.)
4
В каждой ячейке указывается наибольшее возможное количество единиц. В результате не должно
получиться более чем т + п-\ заполненных ячеек, где т — количество строк, n — количество столбцов.

335
Анализируя распределение потребностей на рис. 7д.7, можно увидеть, что при
использовании этого метода некоторые ячейки с высокими издержками оказываются
заполненными, а другие ячейки с низкими затратами остаются пустыми. Этого и
следовало ожидать, поскольку данный метод не учитывает издержки транспортировки, в
результате чего и упрощается алгоритм распределения.
Распределение методом наименьших затрат
В соответствии с данным методом как можно большее значение проставляется в
ячейке с наименьшими затратами. Связи при этом могут нарушаться произвольно. Строки
и столбцы, распределенные полностью, во внимание не принимаются, и процесс
распределения продолжается. Заканчивается данная процедура после того, как все
потребности будут распределены по строкам и столбцам. Распределение по данному
методу иллюстрируется на рис. 7д.8. (Первыми указываются значения в ячейке с
координатами А-Е, затем в C-G, далее в D-H, в В-F и т.д.)
Распределение методом приближений Фогеля
Метод приближений Фогеля (Vogel's Approximation Method — VAM) также основан
на распределении потребностей с учетом затрат на транспортировку. Процесс
распределения осуществляется в пять следующих этапов.
Этап 1. В каждой строке и в каждом столбце, включая фиктивные, определите
разницу между двумя наименьшими значениями затрат на транспортировку в ячейках
каждой строки и каждого столбца.
Этап 2. Определите столбец или строку с наибольшей разницей.
Этап 3. Вставьте наибольшее возможное значение единиц в ячейке с наименьшими
затратами в строке или столбце с самой большой разницей, выбранной на этапе 2.
Этап 4. Прекратите процесс, если удовлетворены все потребности строк и столбцов.
В противном случае переходите к следующему этапу.
Этап 5. Пересчитайте разницу между оставшимися незаполненными двумя ячейками
с наименьшими затратами в каждой строке и в каждом столбце. При вычислении
дальнейшей разницы не следует учитывать строки и столбцы с нулевыми показателями
потребности или поставок. Вернитесь к этапу 2.
Метод приближений Фогеля обычно позволяет получить оптимальное или близкое к
оптимальному исходное решение. Одно из исследований показало, что данный метод дает
оптимальное решение для 80% задач. (Наши студенты утверждают, что остальные 20% —
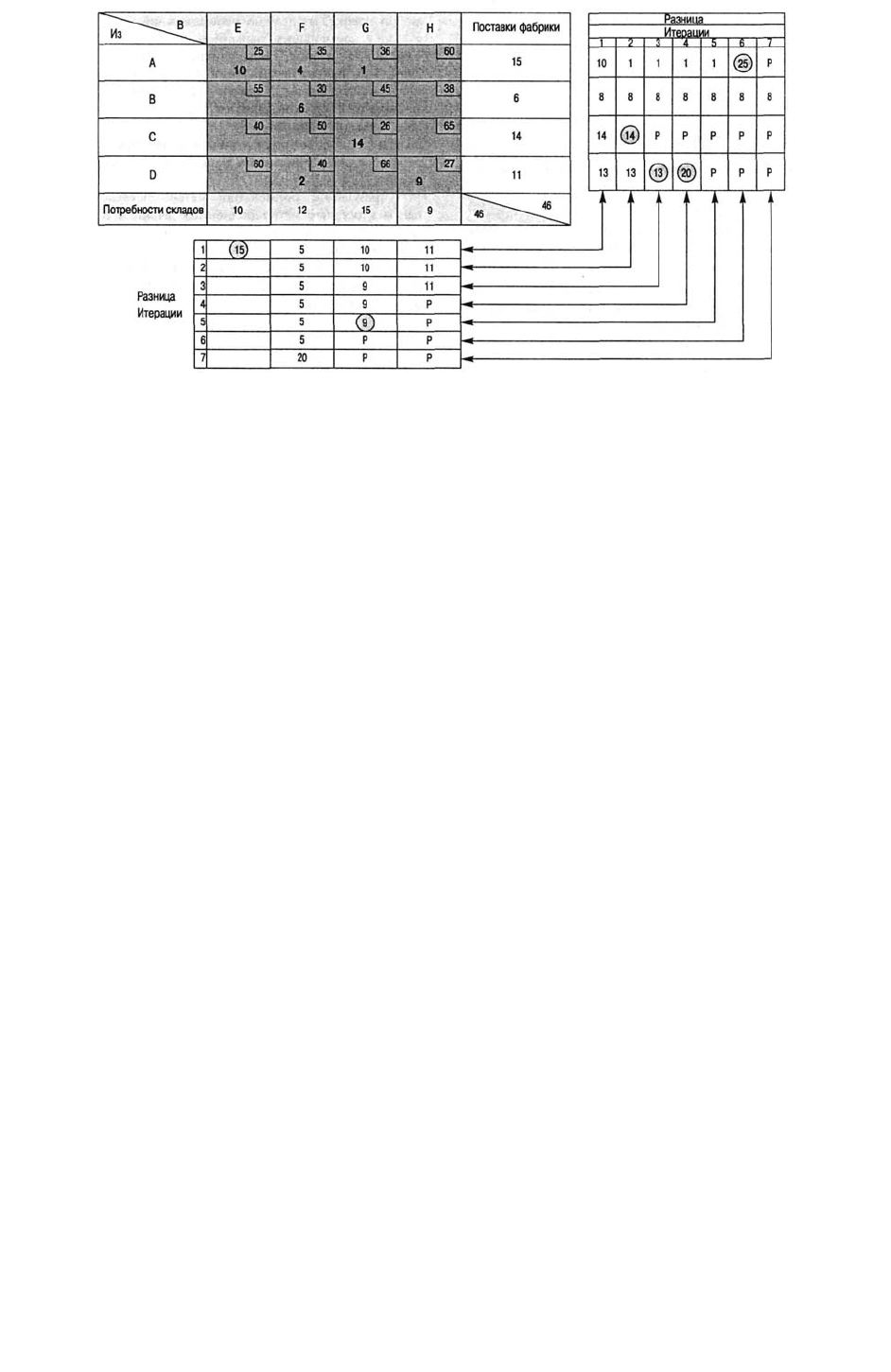
это как раз те задачи, которые попадаются им на экзаменах.) На рис. 7д.9
проиллюстрировано применение метода Фогеля для решения рассматриваемой нами
задачи. (Первыми указаны значения в ячейке А-Е, затем в C-G, далее в D-H, в D-F И Т.Д.)
Обратите внимание, что это исходное решение совпадает с оптимальным, которое
получено в результате всех возможных улучшений исходного размещения, выполненного
методом верхней левой ячейки (сравните дальше с рис. 7д.12).
Стадия III. Получение оптимального решения
Поиск оптимального решения в транспортной задаче заключается в оценке каждой
неиспользованной ячейки и определении, не будет ли перемещение в нее выгодным с
точки зрения уменьшения общих затрат. Если это так, перемещение выполняется и
процесс повторяется. Задача считается решенной после того, как все ячейки оценены и
проведены все соответствующие перемещения.
336
Метод последовательных шагов
Одним из распространенных методов оценки ячеек является метод
последовательных шагов, или метод "подводных камней". Это название появилось в
первых описаниях метода, в которых незаполненные ячейки сравнивались с водой, а
заполненные — с камнями, по аналогии с переходом через ручей с камня на камень. Мы
применим этот метод к поиску решения для исходного размещения, выполненного
методом северо-западной ячейки и приведенного для нашей задачи на рис. 7д,8.
Этап 1. Выберите любую пустую ячейку и укажите замкнутый путь, ведущий к ней.
Этот путь состоит из горизонтальных и вертикальных линий, которые ведут от пус той
ячейки через другие обратно к ней же
5
. В замкнутом пути может быть только одна пустая
ячейка, которую мы и рассматриваем. Повороты пути на 90° могут производиться только
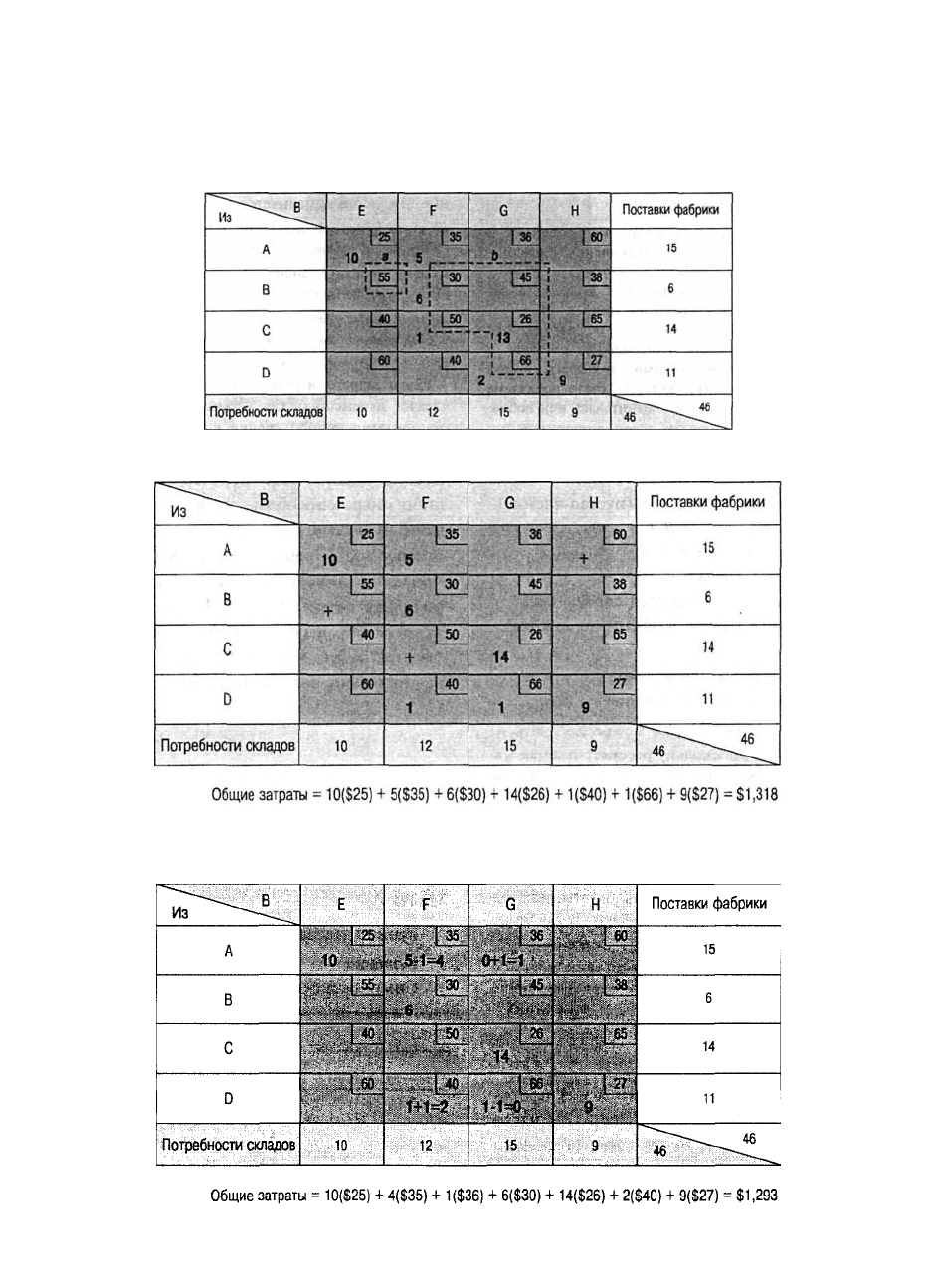
в ближайших (к пустой) заполненных ячейках. На рис. 7д. 10 показаны два замкнутых
пути. Замкнутый путь а необходим для оценки пустой ячейки В-Е; замкнутый путь b
нужен для оценки пустой ячейки А-Н.
5
Если распределение было сделано правильно, в матрице содержится только один замкнутый путь для
каждой ячейки.
Общие затраты = 10($25) + 5($35) + 6($30) + 1($50) + 13(526) + 2($66) + 9($27) = $1,368
Рис. 7д. 7. Распределение методом северо-западной ячейки
Общие затраты = 10($25) + 14($26) + 9(S27) + 6($30) + 5($35) + 1($40) + 1 ($66) = $1,318
Рис. 7д.8. Распределение методом наименьших затрат
337
Total cost = 10($25) + 14($26) + 9($27) + 2($40) + 1($36) + 4($35) + 6($30) = $1,293
Рис. 7д. 9. Распределение методом приближений Фогеля
Этап 2. Переместите одну единицу из заполненной ячейки в угле замкнутого пути в
пустую ячейку и измените оставшиеся заполненные ячейки в других углах в соответствии
с выполненным перемещением
6
. Изменение заключается в добавлении и вычитании
единиц из заполненных ячеек способом, при котором не нарушаются указанные общие
ограничения в отношении поставок и потребностей. Для этого необходимо, чтобы из
каждой строки или столбца, в ячейки которых была добавлена или вычтена единица,
обязательно вычиталась или добавлялась одна единица, но из других ячеек, лежащих на
пути. Таким образом, для пути а потребуются следующие добавления и вычитания.
6
Для проверки возможности перемещения можно добавить не одну, а больше единиц. Однако, поскольку
рассматриваемая нами задача носит линейный характер, если возможно смещение на одну единицу, то будет
возможным смещение и на большее число единиц, и наоборот.
Прибавьте одну единицу в ячейке В-Е (пустая ячейка).
Вычтите одну единицу из ячейки B-F.
Прибавьте одну единицу в ячейке A-F.
Вычтите одну единицу из ячейки А-Е.
Для более длинного пути b потребуется следующее.
Прибавьте одну единицу в ячейке А-Н (пустая ячейка).
Вычтите одну единицу из ячейки D-H. Прибавьте одну единицу в ячейке D-G.
Вычтите одну единицу из ячейки C-G. Прибавьте одну единицу в ячейке C-F. Вычтите
одну единицу из ячейки A-F.
Этап 3. Определите, желательно ли данное перемещение. Это легко выполняется с
помощью
• суммирования значений затрат в ячейке, к которой была добавлена единица;
• суммирования значений затрат в ячейке, из которой была вычтена единица;
• получения разницы между этими двумя суммами, благодаря чему можно
определить, сократились ли как-нибудь затраты.
Если затраты в результате перемещений сократились, следует переместить как
можно больше единиц из оцененной заполненной ячейки в пустую. Если же затраты
повысились, никаких перемещений делать не стоит, а пустую ячейку надо перечеркнуть
или пометить каким-либо иным способом, чтобы показать, что ее уже оценивали.
(Обычно для обозначения ячейки, которая прошла оценку в ходе решения задач
минимизации затрат и была признана нежелательной для перемещения, пользуются
большим знаком "плюс". В этих же случаях при решении задач максимизации прибыли
используют большой знак "минус".) Для ячейки В-Е такие плюсы и минусы будут

338
расположены следующим образом:
+ -
$55 (В-Е) $30 (B-F)
35 (A-F) 25 (A-F)
$90 $55
Для ячейки A-F эти знаки будут расставлены так:
+
-
$60(А-Н) $27(D-H)
66 (D-G) 26 (C-G)
50 (C-F) 35 (A-F)
$176 $88
Таким образом, в обоих случаях очевидно, что перемещений в любую пустую ячейку
делать не следует, так как получаемые разности положительны.
Этап 4. Повторяйте этапы 1—3 до тех пор, пока не будут оценены все пустые
ячейки. Чтобы проиллюстрировать технику выполнения перемещения, рассмотрите
ячейку D-F и короткий замкнутый путь, ведущий к ней: C-F, C-G и D-G Плюсы и минусы
в данном случае будут расставлены следующим образом:
+ -
$40 (D-F) $50 (C-F)
26 (C-G) 66 (D-G)
$66 $116
Поскольку в данном случае вы имеем экономию в размере 50 долл. при доставке по
пути D-F, в эту ячейку следует переместить как можно больше единиц. При этом, однако,
в данном конкретном случае максимально можно переместить только одну единицу,
поскольку максимальное количество единиц, которое можно добавить к
любой ячейке, не должно превышать число, указанное в ячейке с наименьшим
значением, из которого будет проводиться вычитание. Невыполнение этого правила
приведет к нарушению ограничений относительно поставок и потребностей задачи. В
нашем случае очевидно, что ограничивающей ячейкой является C-F, поскольку она
содержит всего одну единицу.
Измененная матрица, отображающая эффект данного перемещения и описанных
выше оценок, изображена на рис. 7д.11.
В результате применения метода последовательных шагов к остальным
незаполненным ячейкам и выполнения указанных перемещений мы приходим к
оптимальному решению.
В частности, незаполненная ячейка A-G на рис. 7д.11 имеет замкнутый путь D-G, D-
F и A-F. Плюсы и минусы будут расставлены так:
+
$36 (A-G) $35 (A-F)
40 (D-F) 66 (D-G)
$76 $101
Поскольку имеется экономия, равная 101 — 76 = 25 долл., мы перемещаем одну
339
единицу в ячейку A-G. На рис. 7д.12 изображена оптимальная матрица для минимальных
транспортных затрат в размере 1293 долл.
Чтобы удостовериться, что полученное распределение действительно является
оптимальным, нам вновь следует оценить каждую пустую ячейку и рассмотреть, желатель
но ли перемещение в нее. Если в каждой из проверенных ячеек окажется знак "плюс", то
задача решена и распределение оптимально.
Рис. 7д. 10. Метод последовательных шагов — определение замкнутого пути
Рис. 7d.11. Измененная транспортная матрица
Рис. 7д. 12. Оптимальное решение транспортной задачи

340
Рис. 7д. 13. Транспортная задача с явлением вырождения
Вырождение
Явление вырождения (Degeneracy) возникает в транспортных задачах, когда
количество заполненных ячеек меньше суммы количества строк и столбцов минус 1 (т.е.
т + п — 1). Вырождение может наблюдаться во время исходного распределения, когда
первое значение в строке или столбце удовлетворяет ограничениям как по строке, так и
по столбцу. Для оценки полученного решения в матрице необходимо определенным
образом скорректировать вырождение. Такая корректировка заключается во вставке
некоторого количества единиц θ в пустые ячейки так, чтобы можно было составить
замкнутый путь для оценки других пустых ячеек. Значение θ может быть бесконечно
малым числом и не оказывать влияния на решение. При этом обычная процедура
предусматривает, что некое значение θ используется точно так же, как реальное число, но
может быть размешено в любую пустую ячейку без соблюдения требований к
ограничениям по строкам и столбцам.
Оптимальное по минимальным затратам на транспортировку решение транспортной
задачи с явлением вырождения показано на рис. 7д.13. На этом рисунке видно, что, если
бы в матрицу не было включено значение θ, некоторые из ячеек оценить было бы
невозможно (включая ту, к которой это значение было добавлено).
После того, как в вводится в решение, это значение остается в нем до тех пор, пока
либо оно не исчезнет при вычитании, либо до получения окончательного решения.
Выбор ячейки, в которую следует вводить θ, принимается произвольно, но можно
сэкономить немало времени, если вставить это значение в ту ячейку, в которой его можно
использовать для оценки как можно большего количества ячеек, не перемещая его. Вы
можете убедиться, что на рис. 7д.13 значение в расположено именно в таком наиболее
выгодном месте.
Альтернативные оптимальные решения
Если оценка пустой ячейки дает в результате то же значение затрат, что и
имеющееся распределение, значит существует равноценное альтернативное оптимальное
решение
7
. В таких случаях управленческий персонал приобретает дополнительную
возможность составлять гибкий окончательный график поставок продукции, используя
два равноценных оптимальных размещения. (Обычно пустую ячейку, определенную как
альтернативный оптимальный маршрут, помечают, например большой цифрой 0.)
7
Учитывая, что все остальные ячейки распределены оптимально.
Резюме
Данное дополнение было в основном посвящено различным процедурам решения
