Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Глава

16.

Управление

запасами

при

зависимом

спросе.

MRP-системы

511

Таблица

16.4.

Будущие потребности в электросчетчиках типов

Аи

В, узлах типа D и детали Е, сформированные на

основе конкретных заказов потребителей и прогнозируемого спроса

Месяц

Заказ

1000

600

300

700

600

700

Счетчик

Прогноз

250

Счетчик

Заказ

400

300

500

400

300

700

Прогноз

Заказ

200

180

250

200

150

160

УзелО

Прогноз

Деталь

Заказ

300

350

300

250

200

Прогноз

Разработка основного

плана

производства

Допустим, количества электросчетчиков и компонен-

тов, указанные в табл. 16.4, необходимые для удовлетво-

рения

известного

спроса, должны поставляться на протя-

жении месяца в соответствии с графиками поставок по-

требителям, а изделия, необходимые для удовлетворения

прогнозируемого

спроса, должны быть готовы уже в первую

неделю месяца.

Предположим также, что все элементы должны быть

готовы в первую неделю месяца. Такое предположение

будет

оправданным, если в нашем примере руководство

компании

предпочитает выпускать электросчетчики по

одной партии каждый месяц, а не несколькими партиями

на

протяжении месяца.

В табл. 16.5 показан пробный вариант основного пла-

на,

основанный на оговоренных выше условиях, причем

потребности на 3-й и 4-й месяцы указаны в первой неде-

ле каждого месяца (обозначены как 9-я и 13-я недели).

Для упрощения предположим, что мы работаем только с

этими

двумя периодами спроса. Разработанный нами

план

необходимо проанализировать на наличие ресурсов,

мощности и т.д., затем, если потребуется, откорректиро-

вать его и повторно выполнить MRP-программу. Будем

считать, что вначале нас устраивает первый вариант ос-

новного плана.

Таблица

16.5.

Основной план, удовлетворяющий по-

требности, указанные в табл. 16.4

Неделя

10 11 12 13 14 15 1В 17

850

550

Счетчик

УзелО

Деталь

1250

460

270

380

360

250

430

560

320

380

Список

материалов

Структура продукта для электрических счетчиков ти-

пов А и В представлена на рис. 16.8 типовым способом —

с помощью кодирования нижнего уровня, когда каждый

элемент помещается на самый нижний уровень, на кото-

ром он появляется в иерархии данной структуры. Элек-

трические счетчики типов А и В состоят из

двух

узлов —

Си

Да также

двух

деталей — Е и F. Числа в скобках

указывают количество, требуемое для производства соот-

ветствующего изделия более высокого уровня.

В табл. 16.6 показан перечень необходимых элементов

формате с отступами, соответствующий

структуре

счет-

чиков типов А и В. Как уже указывалось в этой главе, для

облегчения вычислений все элементы в ВОМ-файле ука-

заны

без использования отступов, однако распечатка с от-

ступами нагляднее демонстрирует способ сборки изделия.

Табл.

16.6.

Перечень деталей для счетчиков А и В в

формате с отступами; в скобках указано

количество деталей, необходимое для

производства соответствующего изделия

более высокого

уровня

СчетчикА

Счетчик

0(1)

£(2)

£(1)

F(2)

0(1)

F(2)

£(1)

0(1)

F(2)

£(1)

Ведомость инвентарных записей

Файл

"Ведомость инвентарных записей" в нашем

примере аналогичен

тому,

который показан на рис. 16.7.

Разница,

как мы уже отмечали в этой главе, состоит в

512

Часть

IV. Управление снабжением

Уровень

Тип

измерителя

0(1)

F(D

Е(2)

Е{1)

0(1)

Tun

F(1)

F(2)

Ed)

F(2)

D(1)

Е(1)

НЦ

F(2)

Рис.

16.8.

Структуры

электросчетчиков

типов

А и В

На рисунке показаны

узлы

детали, входящие

состав электросчетчиков,

а в

скобках указано количество,

нужное для изготовления соответствующего

узла

более

высокого уровня.

том, что настоящий файл "Ведомость инвентарных запи-

сей"

содержит много дополнительных данных: наимено-

вание

поставщика, затраты и время выполнения заказа. В

нашем

примере данные, содержащиеся в файле "Ведо-

мость инвентарных записей", представляют собой налич-

ный

запас на момент начала выполнения программы и

циклы

выполнения заказов. Будем считать, что эти дан-

ные

взяты из файла "Ведомость инвентарных записей" и

показаны

в табл. 16.7.

Таблица

16.7.

Наличное количество изделий и циклы

выполнения

заказа,

которые должны

существовать в файле "Ведомость ин-

вентарных

записей"

Элемент

Наличный

запас

Время

выполнения

заказа

(недели)

Выполнение программы МНР

Итак,

правильные условия

для

выполнения компьютер-

ной

программы

MRP

нами

уже

установлены. Потребности

конечных изделиях определены

помощью основного

плана

производства, состояние запасов

циклы выполне-

ния

заказов находятся

файле "Ведомость инвентарных

записей",

файл "Список материалов" содержит данные,

отражающие

структуру

продукта. Теперь программа

MRP

— в

соответствии

ВОМ-файлом

и с

файлом

"Ведомость инвентарных записей"

—

"разворачивает",

уро-

вень

за

уровнем, потребности

изделиях. Чтобы

учесть

время выполнения заказа, удовлетворяющего чистые

по-

требности,

дата

его

выдачи отодвигается

на

более ранний

срок.

Заказы

на

детали

узлы добавляются

помощью

файла

"Ведомость инвентарных записей", минуя

при

этом

основной

план производства, который обычно

не

опускает-

ся

до

такого уровня детализации, который отражал

бы

по-

требности

деталях

компонентах.

В табл.

16.8

показаны запланированные даты выдачи

заказов

для

этого конкретного "прогона" программы.

Приведенные

ниже пояснения раскрывают работу

про-

граммы.

своем анализе

мы

ограничимся задачей удовле-

творения

общих потребностей

случае

изготовления

1250

счетчиков

А, 460

счетчиков

В, 270

узлов

D и 380

деталей

—

все в

течение

9-й

недели.

Поскольку

запасе есть

готовых счетчиков

А,

необ-

ходимо изготовить

еще 1200

счетчиков

А.

Чтобы получить

счетчики

А на 9-й

неделе, заказ нужно разместить

на 7-й

неделе,

так

как необходимо

недели

на

выполнение зака-

за. Такая

же

процедура касается счетчика

(выдача заказа

на

400

счетчиков

планируется

на 7-ю

неделю).

Необходимым условием начала производства любого

изделия является наличие всех входящих

него компонен-

тов. Таким образом, запланированный срок выдачи заказа

на

изделие

целом определяет соответствующий срок

об-

щей

потребности

во

входящих

него компонентов.

Как

следует

из рис. 16.8

(уровень

1), для

каждого

из

счетчиков

А и В,

которые

данном

случае

называются

"родительскими", требуется

по

одному

узлу С.

Следова-

тельно, общая потребность

в С на 7-й

неделе составляет

1600 узлов

(1200 для А и 400 для В).

Принимая

во

внима-

ние

наличие

узлов

запасе

время выполнения зака-

за, равное одной неделе, приходим

выводу,

что на 6-й

неделе надо заказать

1560

узлов

С.

Анализ уровня

2 на рис. 16.8

показывает,

что

один

узел

необходим

для

каждого изделия

А и

каждого

узла

С.

Таким образом,

для

изготовления

1200

счетчиков

не-

обходимо

1200

узлов

которые представляют собой

об-

щую потребность

узлах

D на 7-й

неделе,

а 1560

узлов D,

необходимые

для

изготовления узлов

С,

представляют со-

бой общую потребность

на 6-й

неделе. Если

самом

на-

чале воспользоваться наличным запасом

принять

во

внимание

время выполнения заказа, равное одной неделе,

то можно прийти

выводу,

что на 5-ю

неделю

следует

запланировать выдачу заказа

на 1530

узлов,

а на 6-ю-

1200 узлов

Глава

16. Управление запасами при зависимом спросе. MRP-системы

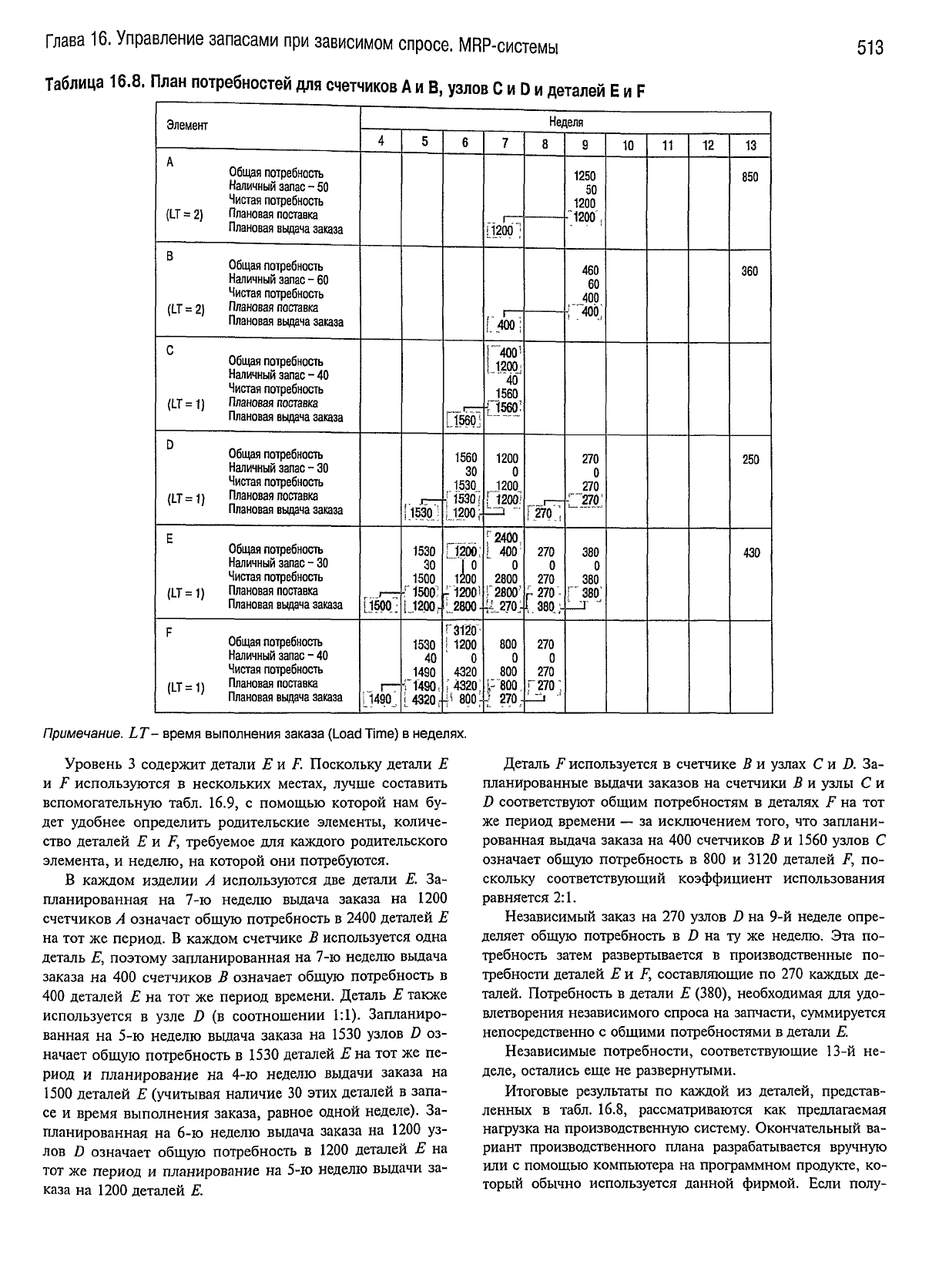
Таблица

16.8.

План

потребностей

для

счетчиков

В,

узлов

и D и

деталей

Е и

513

Элемент

Общая потребность

Наличный запас

Чистая потребность

(LT

2) Плановая поставка

Плановая выдача заказа

Общая потребность

Наличный запас

Чистая потребность

(LT

2) Плановая поставка

Плановая выдача заказа

Общая потребность

Наличный запас

Чистая потребность

(LT

1) Плановая поставка

Плановая выдача заказа

Общая потребность

Наличный запас

Чистая потребность

(LT

1) Плановая поставка

Плановая выдача заказа

Общая потребность

Наличный запас

Чистая потребность

(LT

1) Плановая поставка

Плановая выдача заказа

Общая потребность

Наличный запас

Чистая потребность

мт

1) Плановая поставка

Плановая выдача заказа

Неделя

[1530]"

1530

1500

•Г

1500]

LiapOr

1530

1490

-Г

1490,

[4320

пш

1560

1530

•[1530»

112ш;-

ЕЗГОО;

То

1200

rf'1200'

2800 -

Г3120"

I 1200

4320

,"4320;

У 800

•

[12001

f 400 ]

Г400

1 1200]

"40

1560

1J560J

1200

Паю)

f2400,

L 400

2800

2800'

•sL2?o;

800

R00.

270-

ш:,

270

Г 270

1380;-

270

270".

1250

1200

-"1200",

460

400

•Г;~4оо;

270

СМ

380

380'

850

360

250

430

Примечание. LT- время выполнения заказа (Load

Time)

неделях.

Уровень 3 содержит детали

EviF.

Поскольку детали Е

F используются в нескольких местах, лучше составить

вспомогательную табл. 16.9, с помощью которой нам бу-

дет удобнее определить родительские элементы, количе-

ство деталей Е и F, требуемое для каждого родительского

элемента, и неделю, на которой они потребуются.

В каждом изделии А используются две детали Е. За-

планированная

на 7-ю неделю выдача заказа на 1200

счетчиков А означает общую потребность в

2400

деталей Е

на

тот же период. В каждом счетчике В используется одна

деталь Е, поэтому запланированная на 7-ю неделю выдача

заказа

на 400 счетчиков В означает общую потребность в

400 деталей Е на тот же период времени. Деталь Е также

используется в

узле

D (в соотношении 1:1). Запланиро-

ванная

на 5-ю неделю выдача заказа на 1530 узлов D оз-

начает общую потребность в 1530 деталей Е на тот же пе-

риод и планирование на 4-ю неделю выдачи заказа на

1500 деталей Е (учитывая наличие 30 этих деталей в запа-

се и время выполнения заказа, равное одной неделе). За-

планированная

на 6-ю неделю выдача заказа на 1200 уз-

лов D означает общую потребность в 1200 деталей Е на

тот же период и планирование на 5-ю неделю выдачи за-

каза

на 1200 деталей Е.

Деталь F используется в счетчике В и

узлах

С и D. За-

планированные

выдачи заказов на счетчики В и узлы С и

D соответствуют общим потребностям в деталях F на тот

же период времени — за исключением того, что заплани-

рованная

выдача заказа на 400 счетчиков В и 1560 узлов С

означает общую потребность в 800 и 3120 деталей F, по-

скольку соответствующий коэффициент использования

равняется

2:1.

Независимый

заказ на 270 узлов D на 9-й неделе опре-

деляет общую потребность в D на ту же неделю. Эта по-

требность затем развертывается в производственные по-

требности деталей

EVLF,

составляющие по 270 каждых де-

талей. Потребность в детали Е (380), необходимая для удо-

влетворения независимого спроса на запчасти, суммируется

непосредственно с общими потребностями в детали Е.

Независимые

потребности, соответствующие 13-й не-

деле, остались еще не развернутыми.

Итоговые результаты по каждой из деталей, представ-

ленных в табл. 16.8, рассматриваются как предлагаемая

нагрузка на производственную систему. Окончательный ва-

риант

производственного плана разрабатывается вручную

или

с помощью компьютера на программном продукте, ко-

торый обычно используется данной фирмой. Если полу-

514

Часть

IV.

Управление

снабжением

Таблица

16.9.

Идентификация

родительских

элементов

для

узлов

деталей

С,

D, Е, F

определение

общих

потребностей

элементах

понедельной

разбивкой

Элемент

Родительский

элемент

Число

изделий

на

один

родительский

Результирующая

общая

элемент

потребность

Распределение

потребностей

по неделям

1200

400

1200

1560

2400

400

1530

1200

800

3120

1200

1530

ченный

вариант плана оказывается невыполнимым, а за-

грузка — неприемлемой, основной план производства кор-

ректируется и MRP-программа выполняет все расчеты еще

раз для нового варианта основного плана.

Развитые MRP-системы

Как

не раз уже подчеркивалось в этой главе, MRP

только планирует материалы. Корректировка плана по ог-

раничениям

производственной мощности проводится с

помощью компьютерных программ, не относящихся к

MRP.

В рассмотренных примерах предполагалось, что

план

отдельно корректировался с

учетом

ограничений на

производственную мощность, после

чего

MRP-программа

выполнялась еще раз. (Ситуация для анализа компании

Nichols,

рассматриваемая в конце этой главы,

предусмат-

ривает

ручную

корректировку плана; 2-й вопрос к этой

ситуации.) Определение потребностей во

всех

других

эле-

ментах и

ресурсах

выходит

за рамки данной системы. В

процессе последующих усовершенствований и доработок

MRP-систем в ее компьютерную программу была введена

функция

управления мощностями рабочих центров, а за-

тем вся система была охвачена информационной обрат-

ной

связью. Мы приведем примеры планирования загруз-

ки

мощности рабочего центра и системы с замкнутым

циклом.

Вслед

за этим мы обсудим системы MRP II и, в

конце,

другие

усовершенствованные версии MRP.

Планирование загрузки мощности раОочего центра

Планирование

загрузки производственной мощности

нужно начинать с рассмотрения маршрутных карт заданий,

предусмотренных для выполнения. На рис. 4.13 в

главе

показана

операционная маршрутная карта сборки плунжера

насоса. Обратите внимание, что на этой карте указывается,

какое и

куда

нужно направить задание, связанные с ним

конкретные операции, а также нормативное время пуско-

наладочных работ и время выполнения в расчете на одно

изделие. Все эти показатели используются при расчете об-

щего объема работ на каждом рабочем центре.

Таким

образом, с одной стороны, в маршрутной карте

установлена последовательность выполнения заданий и

определено

требуемое

производственное оборудование по

каждому из них, а с

другой

— каждый рабочий центр со-

держит перечень технологически однородных заданий,

которые

могут

быть выполнены на нем. Задания, направ-

ляемые на рабочий центр, должны быть однотипными и

использовать один и тот же набор инструмента и оснаст-

ки.

Задача загрузки производственной мощности заклю-

чается лишь в правильном построении календарного гра-

фика

выполнения заданий, т.е. в отыскании такой после-

довательности их выполнения, чтобы все они

выполнялись вовремя. (Правила приоритетного планиро-

вания

мы обсудим в

главе

17.) В

случае

нехватки произ-

водственной мощности решение этой задачи

предусмат-

ривает корректировку графика, в процессе которой вы-

равнивается загрузка мощности и исключаются

возможные запаздывания при выполнении заданий.

В качестве примера в табл. 16.10 представлены данные

по

рабочему центру А, за которым закреплено выполне-

ние

различных заданий. Внизу таблицы приведен расчет

доступной мощности за неделю

(161,5

нормо-часов). В

таблице показано планирование заданий в нормо-часах на

три недели, из которого видно, что план

двух

недель

меньше доступной мощности рабочего центра, а план од-

ной

(11-й) недели превышает мощность.

В табл. 16.10 применяются такие понятия, как

коэф-

фициент

использования

(Utilization) и

эффективность

(Efficiency). Разные авторы вкладывают в эти понятия

разный смысл, нередко противоположный. В данном слу-

чае "коэффициент использования" отражает фактическое

время использования оборудования, а "эффективность"

подразумевает использование производственных возмож-

ностей оборудования. Эффективность обычно определя-

ется по сравнению с неким стандартным выходным ре-

Глава

16. Управление запасами при зависимом спросе. MRP-системы

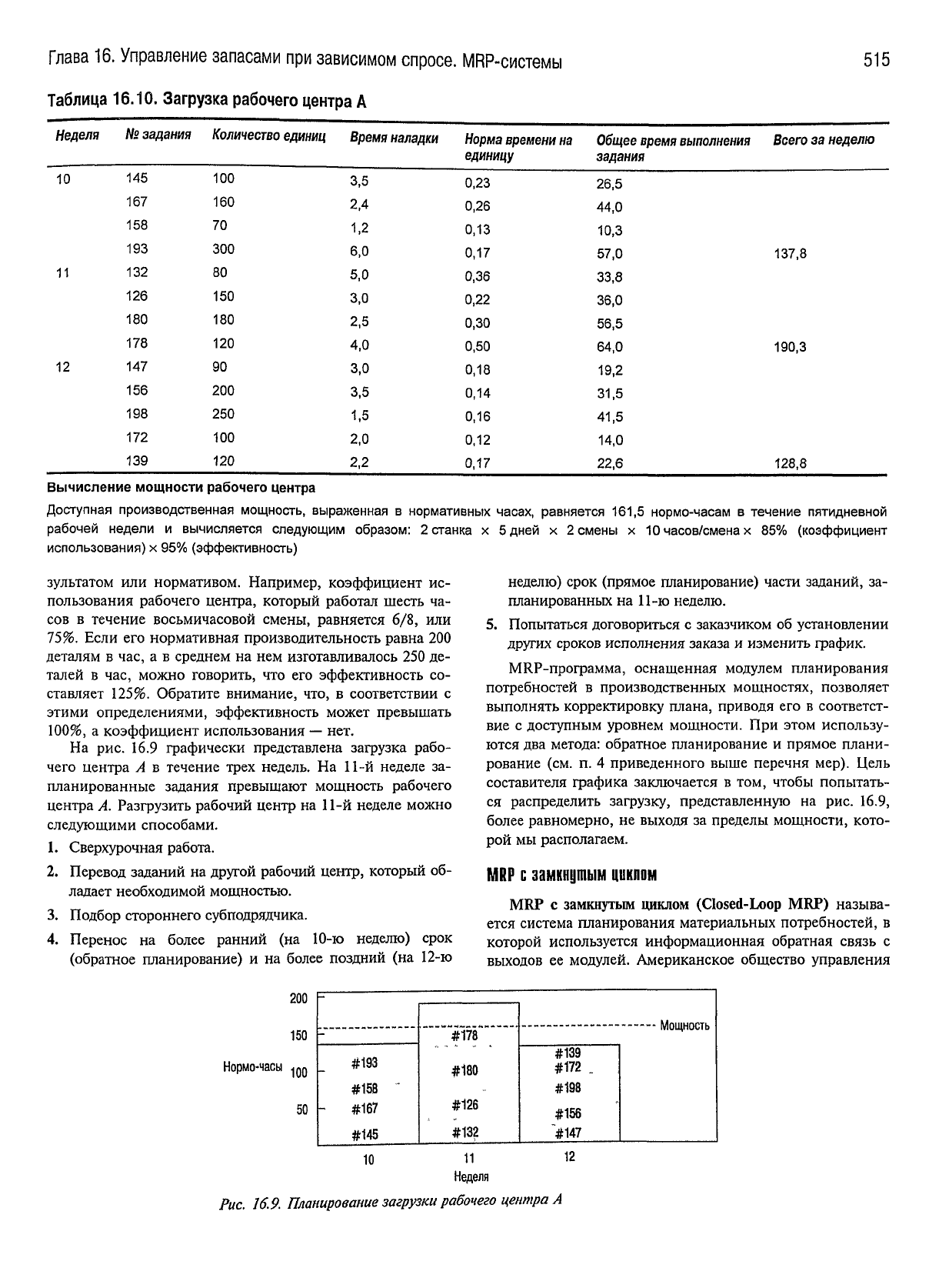
Таблица

16.10.

Загрузка рабочего центра А

515

Неделя

№

задания

145

167

158

193

132

126

180

178

147

156

198

172

139

Количество

единиц

100

160

300

150

180

120

200

250

100

120

Время

наладки

3,5

2,4

1,2

6,0

5,0

3,0

2,5

4,0

3,0

3,5

1,5

2,0

2,2

Норма

времени

на

единицу

0,23

0,26

0,13

0,17

0,36

0,22

0,30

0,50

0,18

0,14

0,16

0,12

0,17

Общее

время

выполнения

задания

26,5

44,0

10,3

57,0

33,8

36,0

56,5

64,0

19,2

31,5

41,5

14,0

22,6

Всего

за

неделю

137,8

190,3

128,8

Вычисление

мощности

рабочего

центра

Доступная

производственная

мощность,

выраженная

нормативных

часах,

равняется

161,5

нормо-часам

течение

пятидневной

рабочей

недели

вычисляется

следующим

образом:

2станка

5дней

2смены

10часов/сменах

85%

(коэффициент

использования)

95%

(эффективность)

зультатом

или

нормативом. Например, коэффициент

ис-

пользования рабочего центра, который работал шесть

ча-

сов

течение восьмичасовой смены, равняется

6/8, или

75%. Если

его

нормативная производительность равна

200

деталям

час,

а в

среднем

на

нем изготавливалось

250 де-

талей

в час,

можно говорить,

что его

эффективность

со-

ставляет 125%. Обратите внимание,

что, в

соответствии

этими

определениями, эффективность может превышать

100%,

коэффициент использования

— нет.

На

рис. 16.9

графически представлена загрузка рабо-

чего

центра

А в

течение

трех

недель.

На 11-й

неделе

за-

планированные задания превышают мощность рабочего

центра

А.

Разгрузить рабочий центр

на

11-й неделе можно

следующими способами.

1. Сверхурочная работа.

2. Перевод заданий на

другой

рабочий центр, который

об-

ладает

необходимой мощностью.

3. Подбор стороннего субподрядчика.

4. Перенос

на

более ранний

(на 10-ю

неделю) срок

(обратное планирование)

и на

более поздний

(на 12-ю

200

150

Нормо-часы

100

неделю) срок (прямое планирование) части заданий,

за-

планированных

на

11-ю неделю.

5. Попытаться договориться

заказчиком

об

установлении

других

сроков исполнения заказа

изменить график.

MRP-программа, оснащенная

модулем

планирования

потребностей

производственных мощностях, позволяет

выполнять корректировку плана, приводя

его в

соответст-

вие

доступным уровнем мощности. При этом использу-

ются два метода: обратное планирование

прямое плани-

рование (см.

п. 4

приведенного выше перечня мер). Цель

составителя графика заключается

том, чтобы попытать-

ся

распределить

загрузку,

представленную

на рис. 16.9,

более равномерно,

не

выходя

за

пределы мощности, кото-

рой мы располагаем.

MRP

с замкнутым циклом

MRP

с замкнутым циклом

(Closed-Loop

MRP)

называ-

ется система планирования материальных потребностей,

которой используется информационная обратная связь

выходов

ее

модулей. Американское общество управления

#193

#158

#167

#145

#178

#180

#126

#132

#139

#172

#198

#156

#147

Мощность

Неделя

Рис. 16.9.

Планирование

загрузки

рабочего

центра

516

Часть

IV.

Управление снабжением

производством

запасами (American Production

and In-

ventory Control Society

—

APICS)

дает

следующее опреде-

ление MRP

замкнутым циклом.

MRP-система

замкнутым циклом

— это

система,

основе

которой лежит определение материальных потребностей;

она

наделена дополнительными функциями планирования сбыта

операций (планирование производства, составление основного

плана производства

планирование потребности

производст-

венных мощностях). Кроме планирования

проверки плана

на

осуществимость, реализуется функция управления,

которой

относятся измерение входной

выходной мощности, составле-

ние подробных графиков

диспетчеризация,

также отчеты

прогнозируемых задержках исполнения заказов

как со

стороны

завода,

так

со

стороны поставщиков, составление графиков

выполнения заказов поставщиками

т.п.

Термин "замкнутый

цикл"

подразумевает

не

только наличие каждого

из

этих

эле-

ментов

системе

целом,

но

обеспечение (управленческой

функцией) обратной связи, которая

любой момент гарантиру-

ет правильность планирования

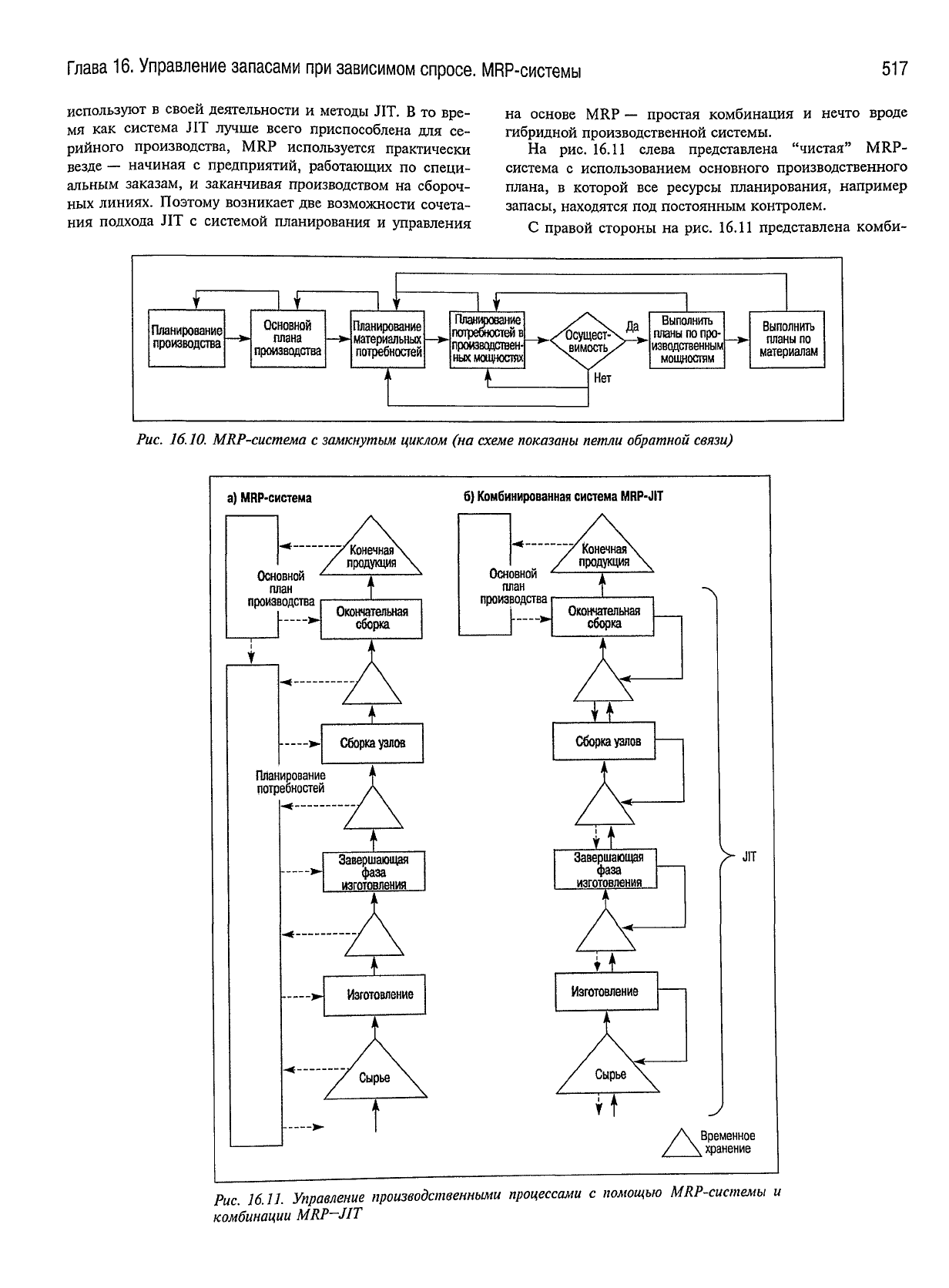
На

рис.

16.10

показана MRP-система

замкнутым

циклом.

Термин "замкнутый цикл" означает,

что

нере-

шенные

задачи

выходные данные поступают обратно

систему

для

проверки

и,

если необходимо, корректиров-

ки.

При этом, как

уже

говорилось

этой главе, источни-

ком

входных данных

для

MRP-системы является основ-

ной

план производства. MRP-программа "разворачивает"

все детали, компоненты

прочие ресурсы, необходимые

для выполнения этого плана. После этого модуль плани-

рования

потребности

производственных мощностях

проверяет результаты выполнения MRP-программы

на

достаточность мощности

для

выполнения составленного

плана.

Если

•

мощность недостаточна,

на

MRP-модуль

по

обратной связи передается информация, указывающая,

что полученный план необходимо скорректировать.

В со-

ответствии

окончательными планами, отражающими

потребности

материалах

мощности,

производствен-

ную систему выдаются заказы. Далее наступает производ-

ственный

этап,

ходе

которого выполняются заказы,

осуществляется мониторинг

сбор данных

ходе

произ-

водства

выполнении заказов,

также оцениваются

ре-

зультаты. Сведения

любых изменениях

производстве,

использовании

мощностей

материалов передаются

об-

ратно

систему.

Планирование производственных ресурсов [МНР

II]

Вполне естественным

ожидаемым развитием систе-

мы

планирования материальных потребностей было

включение

в нее

других

частей

функций производст-

венной

системы. Вначале ввели функцию закупок. Затем

более подробное отражение

до

уровня цеха получила сама

производственная система,

области управления введены

функция

диспетчеризации

составление детальных про-

изводственных графиков. Кроме того, MRP

уже

включало

ограничения

по

мощности рабочего центра, поэтому

ста-

ло очевидным,

что

название

планирование

материальных

потребностей

теперь

не

отражает возможностей расши-

ренной

системы. Кто-то, по-видимому,

это был

Олли

Уайт

(Ollie

Wight),

предложил обновленной

усовершен-

ствованной

MRP-системе название

планирование

производ-

ственных

ресурсов

(Manufacturing Resource Planning

—

MRP IF),

которое лучше отражало новое содержание сис-

темы. Вот что говорит

об

этом сам Уайт.

Надо

ли

идти

портному,

если

вам

понадобились носки?

Да, если

вы

хотите, чтобы они пришлись

вам

точно

но

note.

Renfro Corporation иодберег

вам

сам)К>

подходящею программу

для

нототения

носкоп.

THifiuif-ijJ

тормипя

л вклягс-ст проекгароиз-

шзс и нрогрлммпрампшсе иклои

кяисктоз,

оптгшшое

па

ГСЛЬСХИХ ИрСЗИОТПГ

ПИП

1ДМНКХ

гсстирсншгак тозяров

группах

• £.ОШ

J1U

ухе

СЭСЛ-1ЛН

СВЭП

Hi*

виможсы

вам

Угмлрнтъ,

v;s;e!]£•:-

НИТЬ

ВДСЯТЬ

*ХХИГС

«УШЪСМН

ПрО-

иед-уръЕ

p.tiv:caij:iiim

ыкаюв

uptr

nepxit

состояния.

iqxirmnKjMissi

пня

поставок к плягестю счетов фгк

Kpowr

mm ми

•

сятпгтмешшй

«росисо

»псль

(ихлазз,

unupum

vcraiio&izю

лгстемд

MRP

клас-

са

'Упл

nsiuriiurr

что

ИЛЗКИГМ^У-

иие нрикзвозстш, управление пра-

1СГ4ТПМИ

intAC

yiiptknirtitte

мпп-

кас осущести-

Ес.ш

BUM

НУЛЛЫ

wu гарантируем вам

высочайшего ка

CORPORATION

"Основное производственное уравнение сводится

поиску

ответов

на

следующие вопросы.

Что мы собираемся производить?

Что потребуется

для

этого?

Что

нас имеется?

Что нам нужно получить?

Отличием

MRPII

было планирование

мониторинг всех

ре-

сурсов производственной фирмы— производства, маркетинга,

финансов

проектно-конструкторских работ—

на

основе систе-

мы

замкнутым циклом

генерирование финансовых показате-

лей. Кроме того, важной особенностью концепции

MRPII

стала

возможность моделирования производственной системы"

Совместимость ИТ с МНР

Как

MRP,

так и JIT

имеет свои преимущества.

На-

сколько

успешно

эти

системы

могут

работать вместе

как

их

объединить?

Как уже

говорилось

этой главе,

большинство крупных производственных фирм исполь-

зуют

MRP. Многие

из

фирм, пользующихся MRP

и за-

нимающихся серийным производством, одновременно

Определение

из

словаря перепечатывается

разрешения

APICS, Inc., APICS

Dictionary,

8th ed., 1995.

Oliver

Wight,

The

Executive's Guide to Successful MRP II

(Williston,

VT: Oliver

Wight,

1982),

pp. 6,

17.

Глава

16. Управление запасами при зависимом

спросе.

MRP-системы

517

используют в своей деятельности и методы ЛТ. В то вре-

мя

как система ЛТ лучше всего приспособлена для се-

рийного производства, MRP используется практически

везде — начиная с предприятий, работающих по специ-

альным заказам, и заканчивая производством на сбороч-

ных линиях. Поэтому возникает две возможности сочета-

ния

подхода ЛТ с системой планирования и управления

на

основе MRP — простая комбинация и нечто вроде

гибридной производственной системы.

На

рис. 16.11 слева представлена "чистая" MRP-

система с использованием основного производственного

плана, в которой все ресурсы планирования, например

запасы, находятся под постоянным контролем.

правой стороны на рис. 16.11 представлена комби-

Планирование

производства

•

Основной

плана

производства

Планирование

материальных

потребностей

Планиювание

потребностей

производствен-

ных мощностях

/6сущестХ

Хвимость/'

Нет

Выполнить

планы

по про-

изводственным

мощностям

Выполнить

планы

по

материалам

Рис.

16.10.

MRP-система

замкнутым

циклом (на

схеме

показаны

петли

обратной

связи)

а)

MRP-система

б) Комбинированная система MRP-JIT

Основной

план

производства

Окончательная

сборка

Основной

план

производства

Сборка

узлов

Планирование

потребностей

Завершающая

фаза

изготовления

Окончательная

сборка

Сборка

узлов

Изготовление

Завершающая

фаза

изготовления

Л.

лт

Временное

хранение

Рис. 16.11.

Управление

производственными

процессами

помощью

MRP-системы

комбинации

MRP-J1T

518

Часть

IV.

Управление снабжением

нированная

MRP-JIT производственная система, где

сверху

показан основной план производства, являющий-

ся

отправным элементом для JIT-системы. Компьютер-

ный

контроль производства

ужесточен

ЛТ-системой, ко-

торая функционирует независимо от MRP и

реализует

уже рассмотренную концепцию системы "точно в срок".

Фактически MRP в такой комбинации

двух

систем ис-

пользуется только для составления основного плана

производства.

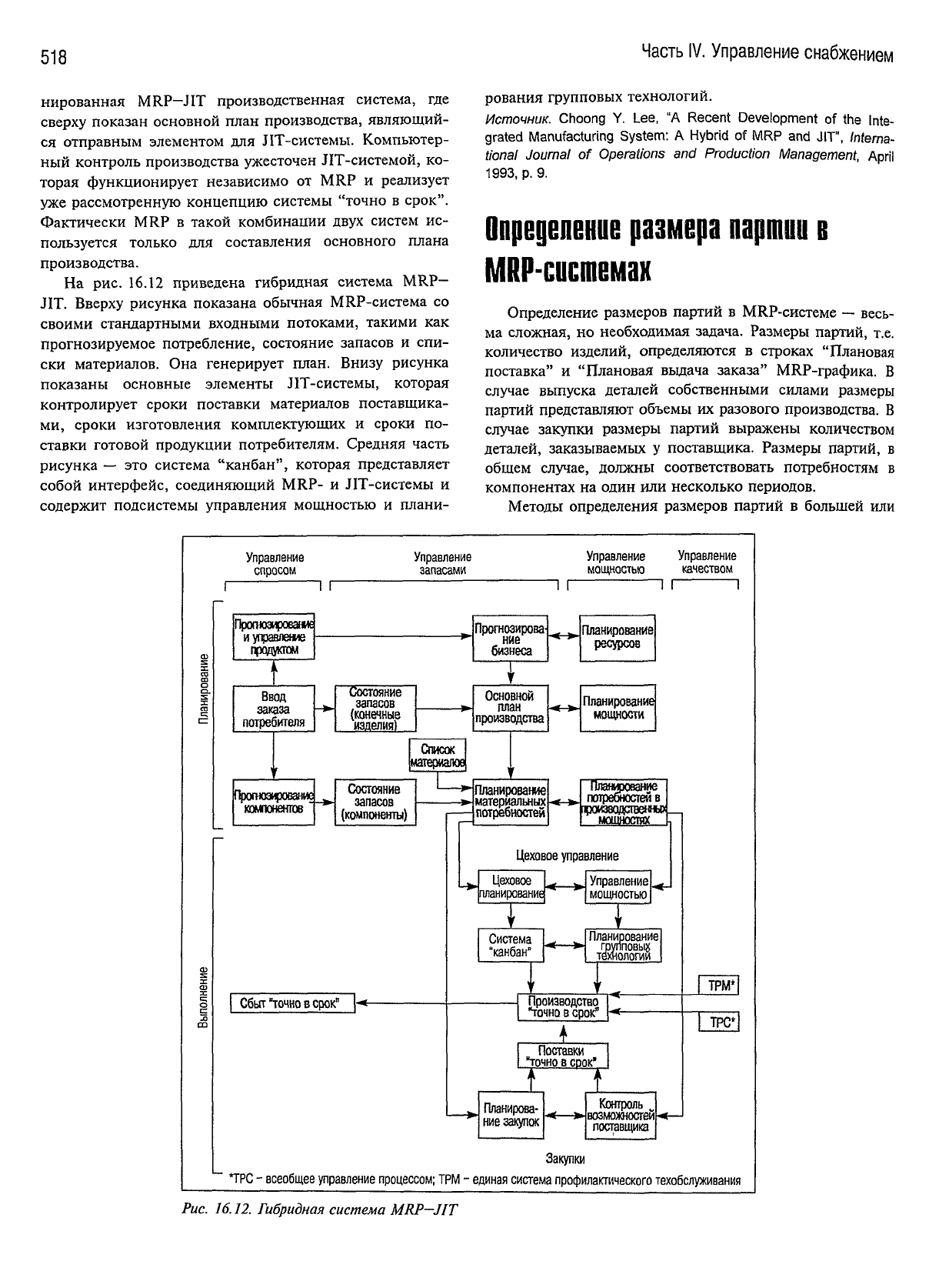
На

рис. 16.12 приведена гибридная система MRP-

ЛТ.

Вверху

рисунка показана обычная MRP-система со

своими стандартными входными потоками, такими как

прогнозируемое потребление, состояние запасов и спи-

ски

материалов. Она генерирует план. Внизу рисунка

показаны

основные элементы JIT-системы, которая

контролирует сроки поставки материалов поставщика-

ми,

сроки изготовления комплектующих и сроки по-

ставки готовой продукции потребителям. Средняя часть

рисунка — это система "канбан", которая представляет

собой интерфейс, соединяющий MRP- и ЛТ-системы и

содержит подсистемы управления мощностью и плани-

рования групповых технологий.

Источник.

Choong

Y. Lee, "A

Recent

Development

of the

Inte-

grated

Manufacturing

System:

Hybrid

of MRP and JIT",

Interna-

tional

Journal

Operations

and

Production

Management,

April

1993, p. 9.

Определение размера партии е

MRP-системах

Определение размеров партий в MRP-системе — весь-

ма сложная, но необходимая задача. Размеры партий, т.е.

количество изделий, определяются в строках "Плановая

поставка" и "Плановая выдача заказа" MRP-графика. В

случае

выпуска деталей собственными силами размеры

партий представляют объемы их разового производства. В

случае

закупки размеры партий выражены количеством

деталей, заказываемых у поставщика. Размеры партий, в

общем

случае,

должны соответствовать потребностям в

компонентах на один или несколько периодов.

Методы определения размеров партий в большей или

Планирование

эинзд

Выпол

Управление

спросом

1 1

Прогнозирование

исправление

продуктам

Ввод

заказа

потребителя

Прогнозирование

компонентов

-»•

—

Состояние

запасов

(конечные

изделия}

Состояние

запасов

(компоненты)

Сбыт

"точно в срок"

Управление Управление Управление

запасами мощностью качеством

II М 1

Список

материалов

—>-

Прогнозирова

ние

бизнеса

Основной

план

производства

Планирование

материальных

потребностей

Планирование

ресурсов

Планирование

мощности

Планирование

потребностей

роизводсгееннь

МОЩНОСТЯХ

Цеховое управление

„ Цеховое

планирование

Управление

мощностью

Система

"канбан"

Планирование

групповых

Производство

"точно в срок"

Поставки

"T04HOBCDOK*

\. ,

„ Планирова-

ние закупок

Контроль

„

•

возможностей«

поставщика

ТРМ*|

ТРС*|

Закупки

*ТРС

всеобщее управление процессом; ТРМ

единая система профилактического техобслуживания

Рис.

16.12.

Гибридная

система

MRP-JIT

Глава

16. Управление запасами при зависимом спросе. MRP-системы

519

меньшей

степени основаны на балансировании затрат на

пуско-наладочные работы или на размещение заказов и

расходов на хранение запаса. Отправной точкой опреде-

ления

размеров партий является чистая потребность в из-

делиях на каждом планируемом интервале MRP-графика.

Многие

MRP-системы позволяют вычислять размеры

партий,

основываясь на некоторых широко распростра-

ненных

методах. Однако очевидно, что определение раз-

меров партий повышает сложность процесса составления

MRP-графиков.

Ниже

мы рассмотрим четыре метода определения раз-

меров партий, воспользовавшись для этого общим приме-

ром.

Мы опишем следующие методы определения разме-

ров партий: метод "партия за партией" (Lot-For-Lot —

L4L), метод экономичного размера заказа (Economic Or-

der Quantity — EOQ), метод наименьших общих затрат

(Least Total Cost — LTC) и метод наименьших удельных

затрат (Least

Unit

Cost — LUC).

Пусть, в качестве примера, для определения размеров

партий

на плановый период, равный восьми неделям,

чистые потребности и затраты

будут

такими.

Понедельные

чистые

потребности:

3 4 5

60 70 60 95

Стоимость

одного

изделия

Затраты

на

пуско-наладочные

работы

или

размещение

заказа

Расходы

на

хранение

запаса

(за

неделю)

Метод

"партия за партиец"

"Партия

за партией" (Lot-For-Lot — L4L) — самый

распространенный

метод. Он обладает следующими свой-

ствами:

•

обеспечивает точное соответствие запланированных

заказов

чистым потребностям;

•

определяет точные потребности на каждую неделю (ни

одно изделие не переходит на последующие периоды);

•

минимизирует расходы на хранение;

$10,00

$47,00

0,5%

от

цены

•

учитывает затраты на пуско-наладочные работы и ог-

раничения

мощности.

В табл. 16.11 представлены вычисления методом

"партия

за партией". Чистые потребности заданы в столбце

2. Поскольку сама логика метода "партия за партией" пре-

дусматривает точное соответствие объема производства

(столбец 3) и требуемого количества (столбец 2), в конце

недели (столбец 4) не должно оставаться никаких запасов,

т.е. никакие запасы не переходят на

следующую

неделю и

расходы на хранение запаса (столбец 5) равны нулю. Одна-

ко

метод "партия за партией" каждую неделю

требует

за-

трат на наладку (столбец 6), которые связаны с тем, что в

течение недели рабочим центром изготавливаются различ-

ные

наименования изделий и для каждого наименования

необходима переналадка оборудования, соответствующая

производимому изделию. Затраты на наладку были бы од-

нократными,

если бы на рабочем центре изготавливался

лишь

один тип изделий и рабочий центр простаивал бы в

ожидании

следующей недели. Поэтому метод "партия за

партией"

вызывает высокие затраты на пуско-наладочные

работы или на размещение заказов.

Метод

экономичного размера заказа

В главе 15 мы уже обсуждали модель EOQ, которая

минимизирует затраты на пуско-наладочные работы и

расходы на хранение. В модели EOQ должен либо обеспе-

чиваться постоянный спрос, либо создаваться резервный

запас,

компенсирующий изменение спроса. Модель EOQ

использует оценку общей годовой потребности, затраты

на

пуско-наладочные работы или затраты на размещение

заказа,

а также годовые расходы на хранение. Модель

EOQ не предназначена для системы с дискретными вре-

менными

периодами, что характерно для MRP-системы.

Методы определения размеров партий, используемые в

MRP,

исходят из того, что потребности в изделиях удов-

летворяются в начале периода. В этом

случае

расходы на

хранение должны относиться только к конечному запасу

этого периода, а не к среднему запасу, как в

случае

моде-

ли

EOQ, которая предполагает, что детали используются

непрерывно

на протяжении всего периода. Размеры пар-

тий,

определяемые моделью EOQ, не всегда охватывают

Таблица 16.

Неделя

11. Вычисления размеров партий

Чистая

потреб-

Объем

произ-

ность

водства

(2)

(3)

методом

"партия

Остающийся

за-

пас

(4)

за

партией"

Расходы

на хра-

нение

(в

долл.)

(5)

Затраты

на налад-

ку (в долл.)

(6)

Общие

затраты

(в долл.)

(7)

0,00

47,00

94,00

141,00

188,00

235,00

282,00

329,00

376,00

520

целое число периодов, например, партия может обеспе-

чить потребности на 4,6 периода.

Воспользовавшись теми же данными, что и в примере

для метода "партия за партией", вычислим экономичный

размер заказа.

Годовая потребность на основе 8 недель составит

D =

525/8

х 52 =

3412,5

изделий.

Годовые расходы на хранение одного изделия:

Н=

0,5% х $10 х 52 недели =

$2,60

на одно изделие.

Затраты на пуско-наладочные работы заданы и состав-

ляют S = $47.

Таким

образом, экономичный размер партии составит

EOQ =

351 изделие.

В табл. 16.12 показан MRP-план, в котором размер

партии равен EOQ, т.е. 351 изделие. Размер партии EOQ

на

1-й неделе достаточен для удовлетворения потребно-

стей с 1-й по 5-ю недели и части 6-й недели. В таком

случае

на 6-ю неделю планируется еще одна партия EOQ,

которая удовлетворяет потребности с 6-й по 8-ю недели.

Обратите внимание, что при методе EOQ остается

неко-

торый запас в конце 8-й недели, который переносится на

9-ю неделю.

Метод наименьших оОщик затрат

Метод наименьших общих затрат (Least Total Cost —

LTC) — многошаговый метод, при котором размер пар-

тии определяется по

результатам

сравнения расходов на

хранение и затрат на пуско-наладочные работы (или за-

трат

на размещение заказа) при различных размерах пар-

тии,

а затем выбирается партия, для которой эти затраты

примерно равны.

В верхней части табл. 16.13 представлены

результаты

расчета размера первой партии по наименьшим общим за-

тратам. Процедура вычисления размеров партии этим ме-

тодом сводится к сопоставлению затрат на наладку и расхо-

дов на хранение при различных количествах недель, пере-

крываемых размером партии. Например, сравниваются

затраты на производство в течение 1-й недели для

удовле-

творения потребностей 1-й недели; производство в течение

Часть IV. Управление снабжением

1-й недели для удовлетворения потребностей 1-й и 2-й н

дели; производство в течение 1-й недели для удовлетворе"'

ния

потребностей 1-й, 2-й и 3-й недели и т.д. Правильным

выбором

будет

размер партии, при котором затраты на на

ладку и расходы на хранение примерно равны, fi

табл. 16.13 оптимальный размер партии равен 335

скольку расходы на хранение, составляющие $38, и затрат"

на

наладку, составляющие $47, оказываются ближе,

чем

$56,25

и $47 ($9 против $9,25). Этот размер партии отвечает

потребностям недель с 1-й по 5-ю. Таким образом, это ме-

тод в принципе аналогичен

методу

EOQ, но в отличие от

него,

размер партии в этом

случае

охватывает

только целые

количества периодов.

Приняв

решение на 1-й неделе разместить заказ

обеспечивающий потребности первых пяти недель, на 6-й

неделе нужно вновь определить, сколько недель в

буду-

щем мы можем обеспечить очередной партией. Из

табл. 16.13 видно, что величины расходов на хранение и

затрат на наладку оказываются самыми близкими, когда

они

охватывают

потребности для недель с 6-й по 8-ю

Обратите внимание, что расходы на хранение и затраты

на

наладку в этом

случае

весьма различаются. Это связано

с тем, что наш пример заканчивается лишь на 8-й неделе.

Если бы "горизонт планирования" был шире, размер пар-

тии,

запланированный на 6-ю неделю, наверное, охваты-

вал бы большее количество недель в

будущем

(во всяком

случае, дело не ограничивалось бы 8-й неделей). В этом

проявляется одно из ограничений как метода LTC, так

LUC

(это ограничение мы обсудим ниже). На оба эти ме-

тода

оказывает влияние широта "горизонта планирова-

ния".

В нижней части табл. 16.13 показаны окончатель-

ные размеры партий и общие затраты.

Метод наименьших

удельных

затрат

Метод наименьших

удельных

затрат (Least

Unit

Cost

LUC)

— многошаговый метод определения размера партии,

при

котором суммарные затраты, определяемые по перио-

дам аналогично предыдущему

методу,

делят на общее чис-

ло изделий за рассматриваемое количество периодов. По-

лученная величина представляет собой удельные затраты,

по

минимуму которых определяется размер партии.

Таблица

16.12.

Вычисление

размеров

партий

методом

экономичного

размера

заказа

Неделя

Чистая

Объем

Остающийся

Расходы

на хра-

Затраты

на

на-

Общие

затраты

потребность

производства

запас нение (в долл.) ладку (в долл.) (в долл.)

351

301

241

171

111

292

232

177

15,05

12,05

8,55

5,55

0,80

14,60

11,60

8,85

47,00

0,00

47,00

0,00

62,05

74,10

82,65

88,20

89,00

150,60

162,20

171,05