Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Дополнение

главе

17.

Моделирование

571

Моделирование превратилось

стандартный инстру-

мент бизнеса.

производственной сфере моделирование

используется

для

составления графиков производства,

оп-

ределения уровней запасов

процедур технического

об-

служивания,

для

планирования производственных

мощ-

ностей, планирования потребностей

ресурсах

плани-

рования

процессов,

также для многого

другого.

сфере

обслуживания моделирование широко используется

для

анализа очередей

планирования операций. Нередко,

когда

ту или

иную проблему

не

удается

решить

помо-

щью аналитических методов,

мы

обращаемся

моделиро-

ванию как

последнему

средству

решения.

Определение моделирования

Несмотря

на то, что

термин

моделирование

(Simulation)

имеет различные значения

зависимости

от

конкретного

применения,

сфере бизнеса

он

обычно означает исполь-

зование компьютера

для

выполнения экспериментов

с мо-

делью

той

или

иной реальной системы

. Эти эксперименты

можно выполнять

еще до

создания реальной системы,

что

должно помочь

ее

проектированию, показать,

как эта

сис-

тема

будет

реагировать

на

изменения правил

ее

функцио-

нирования,

оценить реакцию системы

на

изменения

в ее

структуре.

Моделирование особенно удобно выполнять

ситуациях, когда масштабы

сложность соответствующей

проблемы затрудняют или вообще

не

позволяют использо-

вать методы оптимизации. Таким образом,

помощью

мо-

делирования

удалось

достаточно широко изучить предпри-

ятия,

работающие

по

специальным заказам

характери-

зуемые сложными проблемами

очередями.

помощью

моделирования

удалось

также изучить определенные типы

проблем, связанных

управлением запасами, организацией

работ

техническим обслуживанием. Впрочем,

мы

упомя-

нули лишь

малую

часть проблем, которые решают

помо-

щью моделирования. Моделирование можно также исполь-

зовать

сочетании

традиционными методами статистики

и науки управления.

Кроме

того, моделирование полезно при обучении

ме-

неджеров

работников принципам функционирования

реальных систем,

при

демонстрации влияния изменений

системных переменных,

при

управлении

реальном

вре-

мени

и при

выработке новых идей, касающихся ведения

бизнеса.

Методология моделирования

На

рис.

17.1

представлена блок-схема важнейших

фаз

проведения исследования

на

основе моделирования.

настоящем разделе

мы

опишем

каждую

из

этих фаз, давая

ссылки

на

ключевые факторы, перечисленные

правой

части блок-схемы.

'Примерами

других

типов моделирования являются авиацион-

ные имитаторы, видеоигры и анимация виртуальной реальности.

Формулирование

задачи

Формулирование задачи применительно

моделирова-

нию

несколько отличается

от

определения задачи

для лю-

бого

другого

инструмента анализа.

сущности,

оно

связа-

но

указанием целей

идентификацией соответствующих

управляемых

неуправляемых переменных изучаемой сис-

темы. Рассмотрим пример рыбной лавки. Цель владельца

такой лавки заключается

максимизации прибыли

от

про-

дажи рыбы. Соответствующей управляемой переменной

(т.е. переменной,

на

которую может оказывать влияние ли-

цо,

принимающее решения) является правило формирова-

ния

заказов; соответствующими неуправляемыми перемен-

ными

являются уровни суточной потребности

рыбе

и ко-

личество проданной рыбы. Можно указать

другие

цели,

например максимизацию прибыли

от

продажи крабов

или

максимизацию

доходов

от

продаж.

Построение

имитационной

модели

Особенностью моделирования, которая отличает

ее от

таких методов, как линейное программирование

или об-

служивание очередей, является то,

что

имитационную

мо-

дель нужно "настраивать"

на

каждую

конкретную

ситуа-

цию.

противоположность имитационной модели,

при

использовании

различных ситуациях модели линейного

программирования нужно только переопределять

целевую

функцию

уравнения ограничений. Более того, уникаль-

ная

природа каждой имитационной модели проявляется

том,

что

процедуры построения

"прогона" модели,

которых

мы

поговорим несколько позже, представляют

собой синтез различных подходов

моделированию;

это

скорее рекомендации,

не жесткие правила.

Определение

переменных и параметров. С

самого начала

построения имитационной модели нужно определить,

ка-

кие

свойства реальной системы должны быть зафиксиро-

ваны

виде

параметров, а

какие

могут

изменяться

ходе

моделирования,

т.е.

служить

переменными.

Если вернуться

нашему примеру

рыбной лавкой,

то

переменными

бу-

дут заказанное количество рыбы, потребность

объем

продажи,

параметрами

—

стоимость рыбы

продажная

цена

рыбы. При моделировании основное внимание,

как

правило, уделяется состоянию переменных

различные

моменты времени, например, ежедневная потребность

рыбе, выраженная

тоннах,

ежедневное количество

проданной рыбы (также

тоннах).

Определение

правил принятия решений.

Совокупности

условий, при которых изучается поведение модели,

— это

есть

правила принятия решений

или, иначе, операцион-

ные правила.

Эти

правила, прямо

или

косвенно, стано-

вятся объектом большинства исследований

моделирова-

нии.

Во

многих моделях правилами принятия решений

выступают правила формирования приоритетов, напри-

мер,

какого потребителя обслужить первым, какую

работу

выполнять первой

и т.п. В

определенных ситуациях

они

имеют немаловажное значение, учитывая большое коли-

чество переменных

системе. Например, правило

фор-

мирования

заказов

на

товарно-материальные запасы

можно сформулировать

так,

чтобы объем заказа зависел

572

Часть

IV.

Управление

снабжением

Ключевые

факторы

Сформулировать задачу

[Построить имитационную модель

Определить значения

переменных и параметров

Цели

исследуемой системы

Переменные, которые влияют на достижение целей

Определение переменных и параметров

Формулирование правил принятия решений

Определение распределений вероятности

Выбор способа наращивания времени

Определение

начальных

условий

Определение продолжительности моделирования

Выполнить моделирование

Оценить результаты

Определить статистические тесты

Сравнение с

другой

информацией

Принятие результатов

моделирования

вовго

исследования

Рис. 17.1.

Важнейшие

фазы

моделирования

от общей величины запаса, от количества изделий, уже

заказанных, но не полученных, от количества изделий,

заказанных из-за неполучения изделий по

предыдущим

заказам, и величины

желательного

резервного запаса.

Определение распределений вероятностей. Для имита-

ционного моделирования можно использовать две катего-

рии распределений — эмпирические плотности распреде-

ления вероятностей и стандартные математические рас-

пределения. Эмпирическая (фактическая) плотность

распределения выводится из наблюдения относительной

частоты

того

или иного события (например, поступления

очередь

или спроса на определенный продукт). Иными

словами, это "узкоспециализированное" распределение,

относящееся лишь к конкретной ситуации (пример пока-

зан на рис.

17.2,А).

Такие распределения должны опреде-

ляться непосредственным наблюдением или подробным

анализом записей. (Как это

делается,

мы покажем на

примере моделирования

очереди

в этой

главе.)

Но зачас-

тую, например спрос, можно довольно точно аппрокси-

мировать тем или иным стандартным математическим

распределением, нормальным или пуассоновским. Такой

подход

существенно

упрощает

сбор данных и

последую-

щую реализацию модели на компьютере.

Пример

17д.1.

Сопоставление

случайных

чисел

со

стандартным

распределением

Чтобы проиллюстрировать, как случайные числа сопостав-

ляются со стандартным распределением, допустим, что днев-

ной

спрос на газеты, продаваемые через автомат розничной

продажи

газет, имеет нормальное распределение (среднее зна-

чение —

55,

стандартное отклонение —

10).

Это распределение

показано

на рис. 17.2Д Сделав такое предположение, для оп-

ределения дневного спроса можно использовать таблицу слу-

чайно распределенных нормальных чисел (или отклонений) в

сочетании со статистической формулой D

= x

+ Z

a (о членах

этой

формулы мы поговорим ниже), полученной из Z-

преобразования,

используемого для входа в стандартную таб-

лицу нормальных чисел . Для сопоставления случайных чисел

со

стандартным распределением используется указанная ниже

последовательность действий.

Решение

Извлеките пяти- или шестизначное число из табл.

17.1.

Вхо-

дами в эту таблицу являются случайные значения отклоне-

ний,

принадлежащие нормальному распределению со сред-

ним

значением, равным нулю, и стандартным отклонением,

равным

Термин

отклонение

от

среднего

значения

обозна-

чает число стандартных отклонений некоторой величины от

ее среднего значения и — в данном случае — представляет

собой

число стандартных отклонений спроса в тот или иной

день от среднего спроса. В приведенной выше формуле для

О„ этим отклонением будет значение для Z в л-й день. Если

мы моделируем первый день и используем первый ввод в

табл.

17.1,

то Zj = 1,23481. Отрицательное значение отклоне-

ния в этой таблице означает лишь то, что соответствующий

уровень спроса (который мы хотим найти с помощью этой ве-

личины) будет меньше, чем среднее значение, а вовсе не то,

что

спрос

будет отрицательной величиной.

2. Подставим указанное значение

Z<,

а также заданные значе-

ния х и

ст

в формулу:

= x

+ Z

где

— дневной спрос в л-й день;

Базовая

формула

имеет

такой

вид: Z =

~^ .

Если

эту

форму-

лу

преобразовать

относительно

х, она

примет

вид:

= /х +

Zo .

Затем,

чтобы

нагляднее

связать

этот

метод

зада-

чей,

рассматриваемой

данном

примере,

мы

подставляем

вместо

х и х

вместо

ц.

Дополнение

главе

17.

Моделирование

573

А.

0.30-

(спрос)

0.20

0.10

"У

• 1

(спрос)

55 65

Дневной

спрос

Рис.

17.2.

Фактическое

и нормальное распределение спроса с одним

Таблица

17.1.

Случайные нормально распределенные числа

В.

0.50

0.25

55 65 75

Дневной

спрос

тем же средним значением

1,23481

1,54221

0,19126

-0,54929

1,14463

-0,63248

-0,29988

-0,32855

0,35331

0,72576

0,04406

-1,66161

0,02629

1,18250

-0,87214

-0,23153

-0,04776

0,31052

-0,93166

0,56176

1,49673

1,22318

1,00826

-2,75470

1,11241

-0,55806

-0,49094

-0,04187

-0,98726

-0,26990

0,52304

0,24826

-1,19941

1,08497

0,04496

-0,00926

-0,94171

0,82752

-0,23812

0,18124

-1,35882

-1,45402

-0,28185

1,16515

-0,28278

1,64410

0,32468

0,34506

0,20790

0,70691

0.16760

-0,17022

2,24938

-0,95339

-0,96893

0,36915

Xav—средний спрос (в данном

примере

—

55);

—

значение стандартного отклонения

(в

данном приме-

ре—10),

—

число стандартных отклонений

от

среднего значения

л-й день.

Таким

образом,

0„ = 55 +

(1,23481

10).

Решаем относительно

12,3481,

67,3481.

Используя различные числа из таблицы, повторяем пп.

1-3

до

тех

пор, пока

не

промоделируем требуемое количество

дней.

Выбор способа наращивания времени (Time Incremen-

ting). В имитационной модели время можно наращивать

фиксированными

или переменными приращениями

(порциями)

времени. При использовании фиксированных

приращений

времени устанавливаются одинаковые при-

ращения

таймера (например, минуты, часы, дни) и про-

цесс моделирования продвигается через фиксированные

интервалы времени — от одного периода времени к сле-

дующему.

В каждый момент, отсчитываемый таймером,

проводится сканирование системы, чтобы выяснить, не

произошли ли за это время какие-либо события. Если

произошли,

то события фиксируются и выполняется на-

ращивание времени; если же никаких событий не было,

то только выполняется

следующее

наращивание времени

на

одну единицу.

При

использовании переменных приращений время,

имитируемое таймером, наращивается на величину, кото-

рая

требуется для инициирования очередного события.

Какому из способов

следует

отдать предпочтение?

Опыт показывает, что использование фиксированных

приращений

времени оказывается предпочтительным в

том случае, когда интересующие нас события происходят

достаточно регулярно или когда количество событий ве-

лико

(как правило, за один и тот же период времени про-

исходит несколько событий). Вообще говоря, использо-

вать способ переменных приращений времени предпочти-

тельнее в тех

случаях,

когда приходится моделировать

относительно небольшое количество событий, происхо-

дящих на протяжении значительного промежутка време-

ни,

поскольку при использовании этого метода требуется

меньшее время работы компьютера

Инышшцш

шальных

значено! переменных н параметров

Значение

переменной по определению меняется в

ходе

моделирования; однако для любой переменной нужно за-

дать

начальное значение. Значение параметра, напомним,

остается постоянным; однако оно также может изменять-

ся,

если в ряде "прогонов" одной и той же модели изуча-

ются несколько вариантов.

Этот способ пропускает интервалы времени,

течение которых

ничего

не

происходит,

сразу

же

переходит

следующему

мо-

менту, когда наступает то или иное событие (события).

574

Часть IV. Управление снабжением

Определение начальных условий. Определение начальных

условий для переменных является одним из важнейших

тактических решений, которые приходится принимать при

моделировании.

Это связано с тем, что совокупность на-

чальных значений "смещает" модель в ту или иную сторо-

ну от интересующей области исследований, в том числе

модель может попасть в область неустойчивого состояния.

Чтобы очистить результаты от ненужных данных и сокра-

тить время вычислений, аналитики используют:

a) исключение данных, генерируемых на начальных

стадиях "прогона" модели,

b) выбор начальных условий путем пробных прогонов

модели в разных областях,

c) выбор начальных условий у подножия склона анали-

зируемой области.

Однако,

чтобы воспользоваться каким-либо из этих

подходов, аналитик должен иметь определенное представ-

ление об ожидаемом диапазоне выходных данных. Таким

образом, аналитик может смещать результаты в желаемую

сторону и, кроме того, привносить собственное суждение

проектирование модели и анализ результатов моделиро-

вания.

Поэтому, если у аналитика есть какая-то

инфор-

мация,

которая имеет определенное отношение к решае-

мой

проблеме, ее необходимо ввести в модель.

Определение продолжительности "прогона". Продолжи-

тельность процесса моделирования, или время "прогона",

зависит от цели моделирования. Возможно, шире

других

распространен подход, когда процесс моделирования про-

должается до тех пор, пока не достигнуто состояние рав-

новесия

с фактическими данными. В нашем примере с

рыбной

лавкой это означало бы, что моделируемые про-

дажи рыбы соответствуют своим обычным относительным

объемам. Другой подход заключается в том, чтобы выпол-

нить

моделирование для заданного периода времени

(например,

месяца, года или десятилетия), а затем по-

смотреть, приемлемы ли условия, создавшиеся в конце

этого периода. Третий подход состоит в том, чтобы

уста-

новить

такую продолжительность "прогона", которая по-

зволяла бы набрать выборку, достаточно большую для

проверки

статистических гипотез. Этот подход рассматри-

вается в следующем разделе.

Оценка

результатов

Выводы, которые можно извлечь из процесса модели-

рования,

зависят не только от степени соответствия моде-

ли

реальной системе, но и от конструкции самой модели

(в

статистическом смысле). В действительности многие

аналитики

рассматривают моделирование как разновид-

ность

проверки гипотез, когда каждый "прогон" модели

позволяет получить один или несколько фрагментов вы-

борки,

подлежащих формальному анализу с помощью

статистических методов

Статистические процедуры, которые широко используются при

оценивании

результатов моделирования, включают дисперсион-

ный

анализ, регрессионный анализ и t-тесты.

В большинстве случаев аналитик располагает опреде-

ленной

информацией, с помощью которой он может

сравнить результаты моделирования: данные о предыду-

щем функционировании реальной системы, данные о

функционировании

подобных систем и собственное ин-

туитивное понимание аналитиком функционирования ре-

альной

системы. Правда, информации, полученной из

этих источников, как правило, часто недостаточно, чтобы

подтвердить выводы, сделанные на основе результатов

моделирования.

Поэтому единственной подлинной про-

веркой

результатов моделирования является качество

функционирования

реальной системы после применения

ней результатов моделирования.

Принятие результатов моделирования

В данном контексте понятием

принятие

результатов

моделирования

(Validation) обозначается этап, на котором

окончательно убеждаются, что моделирование выполнено

правильно

и результаты соответствуют действительности

или,

иначе, что соответствующая компьютерная интер-

претация

является правильным отображением модели,

построенной

на основе блок-схемы, и что данная модель

адекватно отражает функционирование реальной систе-

мы.

Принять результаты моделирования можно, убедив-

шись,

что в программе

отсутствуют

ошибки программи-

рования

и логические ошибки в самой программе. Ошиб-

ки

программирования выявить сравнительно несложно,

так

как в этом

случае

компьютерная программа просто не

будет

выполняться. Однако ошибки в логике программы

найти

гораздо сложнее, поскольку в таких случаях про-

грамма выполняется, выдавая неправильные результаты, и

однозначно

утверждать, что результаты неверны, без до-

полнительной

проверки нельзя.

Для того чтобы согласиться с результатами моделиро-

вания,

у аналитика есть три варианта действий.

1. Распечатать все вычисления и проверить эти вычисле-

ния

отдельно (может быть, вручную).

2. В модель ввести такие исходные данные, для которых

уже есть фактические результаты, и сопоставить полу-

ченные

результаты моделирования с фактическими.

3. Выбрать определенную точку в процессе моделирования

и,

подобрав для нее соответствующую математическую

модель, рассчитать выходные данные и сравнить резуль-

таты расчета и моделирования для этой точки.

Несмотря

на то, что первых два варианта имеют оче-

видные недостатки, применяются они гораздо чаще, чем

третий вариант, поскольку, если бы действительно суще-

ствовала "соответствующая математическая модель", то,

наверное,

можно было бы решить данную

задачу,

не при-

бегая к моделированию.

Проведение новых исследование

Основываясь

на полученных

результатах

моделирова-

ния,

аналитик может принять решение о проведении еше

одного исследования. При этом можно изменить множе-

ство факторов: параметров, переменных, правил принятия

решений,

начальных условий и продолжительности

Дополнение к главе 17. Моделирование

575

"прогона"

модели.

Что

касается параметров,

то у

анали-

тика

может возникнуть желание повторить моделирова-

ние

несколькими вариантами затрат или

цен

продукта

посмотреть,

как эти

изменения повлияют

на

результаты

моделирования.

Проверка различных правил принятия

решений,

очевидно, заинтересует аналитика, если исход-

ный

вариант правил принес

ему

неудовлетворительные

результаты

или

если первый "прогон" модели заставил

его взглянуть

на

проблему по-новому. Попутно

следует

отметить,

что

процедура использования

при

моделирова-

нии

одного

того

же

потока случайных чисел выступает,

вообще говоря, прекрасным средством

для

выявления

различий

между

проверяемыми вариантами

и к

тому

же

позволяет сократить продолжительность "прогона" моде-

ли.

Кроме того, значения, взятые

из

предыдущего иссле-

дования,

могут

оказаться удачными начальными условия-

ми

для

последующих экспериментов.

Новое

исследование модели отличается

от

простого

повторения

тем, что

существенно меняются параметры,

исходные условия

другие

факторы, приводящие

появ-

лению

на

выходе

новых событий. Может случиться,

на-

пример,

так, что

система имеет

не

один,

несколько

ус-

тойчивых уровней функционирования,

и что

достижение

второго уровня является лишь вопросом времени,

т.е.

продолжительности "прогона" модели. Таким образом,

то время

как

первая серия "прогонов"

из,

скажем,

100

периодов,

обнаружила наличие определенной стабильной

области, удвоение продолжительности серии может

вы-

явить

новые

существенно отличные

от

предыдущих

—

хотя

и не

менее стабильные

—

области.

этом

случае

выполнение

моделирования

продолжительностью,

рав-

ной

200

временным периодам, может рассматриваться

как

новое

исследование модели.

Компьютеризация

Используя

ту

ИЛИ

иную

компьютерную модель, мы сво-

дим

исследуемую

систему

некоторому

ее

символиче-

скому представлению

компьютере. Несмотря

на то, что

авторы этой книги

не

собираются вдаваться

техниче-

ские

аспекты компьютерного моделирования, некоторые

из

них все же

непосредственно относятся

проблеме

изу-

чения

систем

помощью имитационных моделей.

част-

ности

назовем только следующие.

1. Выбор компьютерного языка.

2. Представление процессов

виде блок-схем.

3. Кодирование.

4. Генерация данных.

5. Выходные отчеты.

6. Подтверждение.

В конце этого Дополнения

мы

поговорим более

под-

робно

программах

языках моделирования.

Выходные отчеты. Использование универсальных

язы-

ков

программирования позволяет аналитику указать

лю-

бой

требуемый

тип

выходного отчета (или данных)

— при

условии,

что

аналитик готов затратить определенные

уси-

лия

на

программирование.

специализированных языках

предусмотрены стандартные подпрограммы, которые

можно

активизировать

помощью

одного-двух

операто-

ров этих языков программирования

благодаря которым

можно

распечатать, например, такие данные,

как

средние

значения,

дисперсии

стандартные отклонения. Однако

каким

бы ни был

язык

программирования, опыт свиде-

тельствует,

что

слишком большой объем данных, полу-

ченных

результате

моделирования, может оказаться

столь

же

непродуктивным

для

решения проблемы,

как и

слишком

малый

их

объем,

— и в том, и в

другом

случае

весьма затруднительно выявить действительно важную

значимую информацию

об

исследуемой системе.

Моделирование

очередей

Очереди, которые бывают последовательными

и па-

раллельными, например, очереди

на

сборочных линиях

на

предприятиях, выполняющих специальные заказы,

как

правило,

невозможно описать

помощью математических

моделей. Однако очереди хорошо поддаются имитацион-

ному моделированию

на

компьютере,

качестве примера

такого моделирования

мы

выбрали

двухэтапную

сбороч-

ную линию.

Пример. Двухэшапиая сборочная пиния

Рассмотрим

сборочную линию,

на

которой проводится

сборка крупногабаритного изделия, такого

как

холодиль-

ник,

микроволновая печь, автомобиль, лодка, телевизор

или

мебель.

На рис. 17.3

показаны

две

рабочие станции

на

такой сборочной линии.

Физические

размеры продукта очень важны

при ана-

лизе функционирования

проектировании сборочной

линии,

поскольку количество продуктов, которые

могут

находиться

на

каждой рабочей станции, влияет

на

произ-

водительность рабочего. Если продукт крупногабаритный,

рабочие станции зависят

друг

от

друга.

На рис. 17.3, на-

пример,

показаны

две

рабочие станции

(7 и 2), на

кото-

рых работают

Боб и

Рэй.

Эти

рабочие станции представ-

ляют

двухэтапную

сборочную линию. Продукция

со

стан-

ции

поступает

на

станцию

Если

эти две

рабочие

станции

расположены рядом

так, что

между

ними

нет

места

для

хранения изделий,

то

медленная работа Боба

будет

тормозить Рэя

— он

будет

простаивать.

наоборот,

если

Боб

работает быстро (или если

Рэя

на

выполнение

операций

уходит

больше времени,

чем у

Боба),

будет

про-

стаивать Боб.

Допустим,

что Боб

(первый рабочий

на

сборочной

ли-

нии)

может брать

на

обработку новое изделие

любой

момент, когда

оно ему

понадобится. Предметом нашего

анализа

будет

взаимодействие

между

Бобом

Рэем.

Цель

исследования. В

результате

этого исследования

мы

должны ответить

на ряд

вопросов, касающихся функцио-

нирования

сборочной

линии.

Вот лишь некоторые

из

них.

• Каково среднее время выполнения каждым

из

работ-

ников

своих операций?

• Какова пропускная способность этой сборочной линии?

576

Часть IV. Управление снабжением

Рис.

17.3.

Две

рабочие

станции

на

сборочной

линии

•

Сколько Бобу приходится ждать Рэя?

•

Сколько Рэю приходится ждать Боба?

•

Если можно было

бы

увеличить расстояние

между

станциями,

чтобы

на

освободившемся месте хранить

продукцию

обеспечить таким образом работникам

определенную независимость

друг

от

друга,

как бы это

повлияло

на

пропускную способность сборочной

ли-

нии,

время ожидания и т.п.?

Сбор

данных.

Чтобы промоделировать

эту

систему,

нужны сведения

производительности Боба

Рэя.

Од-

ним

из

способов получить эти данные является деление

определенного, достаточно большого, промежутка време-

ни

на ряд

одинаковых интервалов

наблюдение

за вы-

полнением

операций каждым

из

рабочих. Затраченное

время

на

выполнение каждой операции измеряется

и от-

мечается

соответствующем интервале значений. По ко-

личеству отметок

каждом интервале строится гисто-

грамма данных.

В табл.

17д.2

представлена форма сбора данных,

ис-

пользовавшаяся для наблюдения

за

работой Боба

Рэя.

Чтобы упростить процедуру сбора, время работы поделено

на

10-секундные интервалы. Наблюдение

за

работой Боба

выполнялось

течение

100

повторений

его

операции,

наблюдение

за

работой Рэя —

течение

повторений

его операции. Количество наблюдений необязательно

должно быть одинаковым

для

каждого рабочего, однако

чем

их

больше

чем меньший размер имеют временные

интервалы,

тем

точнее

будет

исследование. Впрочем,

"платой"

за

большое количество наблюдений

малый

размер интервалов времени

будет

большая продолжитель-

ность наблюдений

необходимость использовать для них

больше людей

(не

говоря

уж

том,

что на

составление

программы

выполнение моделирования

этом

случае

также

уйдет

больше времени).

В табл. 17д.З представлены назначенные интервалы

случайных чисел, соответствующие данным фактических

наблюдений.

Для

упрощения представления

дальней-

ших расчетов временные интервалы заменены

на их

средние значения

и к

ним

относятся соответствующие

фактические

частоты появления случаев.

Например,

Бо-

ба было четыре 10-секундных случая

из

общего

их

числа,

равного 100. Для первого 10-секундного интервала можно

было

бы

назначить любые

числа

из 100,

например под

номерами

42,

18, 12 и

93. Однако специально заниматься

выбором таких чисел

для

образования статистического

ряда

не

имеет смысла, достаточно назначать числа,

сле-

дующие подряд, например 00, 01,

02 и

03.

Для Рэя выполнено всего

наблюдений. Существует

два способа назначения случайных чисел

для Рэя. Во-

первых,

мы

могли

бы

использовать именно

чисел

(например,

00—49)

игнорировать числа,

не

входящие

Таблица

17д.2.

Секунды

5-14,99

15-24,99

25-34,99

35-44,99

45-54,99

55-64,99

65-74,99

75-84,99

Форма

для сбора

данных

при

наблюдении

за трудом рабочего

Боб

Наблюдения

НИ

Illll

Hill Mill

Illll Illll Illll Illll

Hill Illll Hill Illll Illll Illll Illll Illll

Illll Illll

Illll

Illl

Всего

ИТОГО

100

Illl

Illll

lilll

Illll

III

Illll

Illl

Всего

Рэй

ИТОГО

Дополнение

главе

17.

Моделирование

Таблица 17д.З

Интервалы

случайных

чисел для Боба и Рэя

577

Секунды

Инте

валыс

^^хчисел

Временные

частоты

для Рэя

Интервалы

случайных

чисел

(операция

Всего

100

00-03

04-09

10-19

20-39

40-79

80-90

91-95

96-99

Всего

= 50

00-07

08-17

18-29

30-43

44-63

64-79

80-91

92-99

этот диапазон. Однако при этом необоснованно пришлось

бы отбрасывать 50% всех чисел из их общего списка. Дру-

гой подход заключается в том, чтобы удвоить число наблю-

дений

при сохранении частот событий. Например, вместо

того чтобы назначать, скажем, числа 00-03, которые учи-

тывали бы 4 наблюдения из 50, относящихся к интервалу

первых 10 секунд, можно назначить числа

00—07,

которые

представляли бы 8 наблюдений из 100 (удвоенное количе-

ство наблюдений, но при той же частоте).

Принимая

во внимание быстродействие современных

компьютеров, потеря времени на прогон модели при та-

ком

удвоении количества наблюдений представляется

весьма незначительной, но зато оба рабочих оказываются

привязанными

к одному и тому же ряду наблюдений.

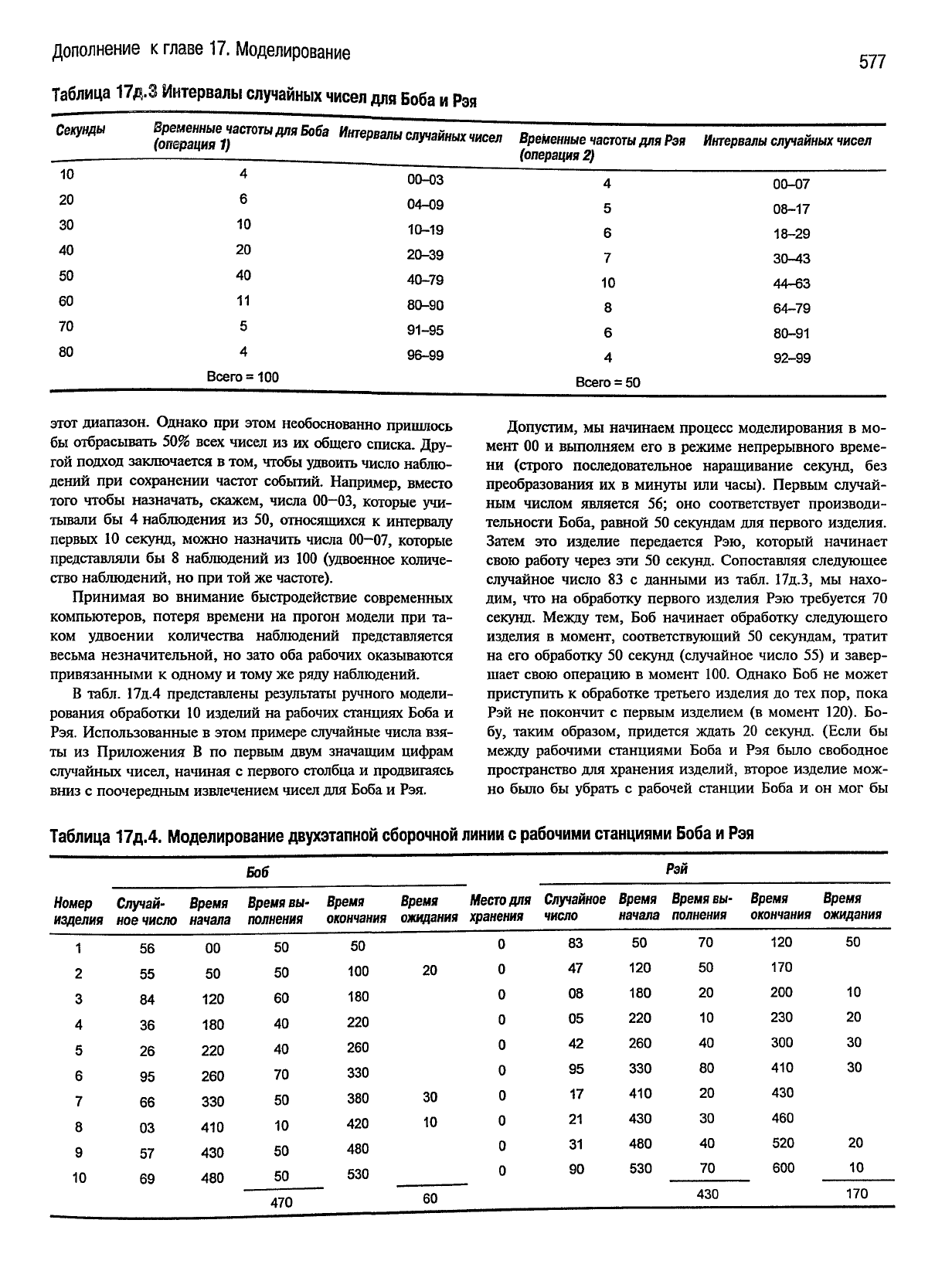
В табл. 17д.4 представлены результаты ручного модели-

рования

обработки 10 изделий на рабочих станциях Боба и

Рэя.

Использованные в этом примере случайные числа взя-

ты из Приложения В по первым

двум

значащим цифрам

случайных чисел, начиная с первого столбца и продвигаясь

вниз

с поочередным извлечением чисел для Боба и Рэя.

Допустим, мы начинаем процесс моделирования в мо-

мент 00 и выполняем его в режиме непрерывного време-

ни

(строго последовательное наращивание секунд, без

преобразования

их в минуты или часы). Первым случай-

ным

числом является 56; оно соответствует производи-

тельности Боба, равной 50 секундам для первого изделия.

Затем это изделие передается Рэю, который начинает

свою работу через эти 50 секунд. Сопоставляя следующее

случайное число 83 с данными из табл. 17д.З, мы нахо-

дим, что на обработку первого изделия Рэю требуется 70

секунд. Между тем, Боб начинает обработку следующего

изделия в момент, соответствующий 50 секундам, тратит

на

его обработку 50 секунд (случайное число 55) и завер-

шает свою операцию в момент 100. Однако Боб не может

приступить к обработке третьего изделия до тех пор, пока

Рэй

не покончит с первым изделием (в момент 120). Бо-

бу, таким образом, придется ждать 20 секунд. (Если бы

между

рабочими станциями Боба и Рэя было свободное

пространство для хранения изделий, второе изделие мож-

но

было бы убрать с рабочей станции Боба и он мог бы

Таблица

17д.4.

Моделирование двухэтапной сборочной линии с рабочими станциями Боба и Рэя

Номер

изделия

Случай-

ное

число

Время

начала

120

180

220

260

330

410

430

480

Боб

Время вы-

полнения

470

Время

окончания

100

180

220

260

330

380

420

480

530

время

ожидания

Место

для

хранения

Случайное

число

Время

начала

120

180

220

260

330

410

430

480

530

Рэй

Время вы-

полнения

430

Время

окончания

120

170

200

230

300

410

430

460

520

600

Время

ожидания

170

578

Часть

IV.

Управление

снабжением

приступить к обработке

третьего

изделия в момент 100.)

Остальная часть этой таблицы вычислена по

тому

же

принципу:

получение случайного числа, нахождение со-

ответствующего

времени обработки, фиксация времени

ожидания (если таковое имеется) и вычисление момента

завершения. Обратите внимание, что при отсутствии ме-

жду рабочими станциями Боба и Рэя свободного про-

странства для хранения изделий простаивать (и довольно

долго)

приходится обоим работникам.

Теперь мы можем ответить на некоторые вопросы, ка-

сающиеся данной линии.

Пропускная

способность системы составляет в сред-

нем 60 секунд на одно изделие (полное время 600 секунд

для Рэя, поделенное на 10 изделий).

Коэффициент

использования времени Боба равняется

470/530

88,7%.

Коэффициент

использования времени Рэя равняется

430/550

= 78,2% (без

учета

начального времени ожидания

первого изделия — 50 секунд).

Среднее время выполнения операции у Боба равняется

470/10

= 47 секунд.

Среднее время выполнения операции у Рэя равняется

430/10

= 43 секунды.

Мы

продемонстрировали, как решить данную

задачу

помощью простого "ручного" моделирования. Тем не ме-

нее,

выборка из 10 изделий слишком мала, чтобы отно-

ситься к ней с большим доверием, поэтому

такую

задачу

лучше

решать на компьютере, задав несколько тысяч из-

делий. Еще один вариант этой задачи мы рассмотрим в

следующем

разделе настоящего Дополнения.

Помимо

этого, крайне важно рассмотреть влияние

пространства для хранения изделий

между

рабочими

станциями.

Сначала можно посмотреть, какими

будут

пропускная способность сборочной линии и

коэффици-

енты использования работников при отсутствии свобод-

ного пространства для хранения изделий

между

рабочими

станциями.

При втором "прогоне" это пространство

можно увеличить с нуля до единицы и зафиксировать со-

ответствующие изменения в поведении модели. Повторе-

ние

"прогонов" для

двух,

трех,

четырех

и т.д. единиц

дает

руководству

предприятия возможность сравнить дополни-

тельные затраты на организацию свободного пространства

эффект от повышения коэффициентов использования

работников. Создание свободного пространства

между

ра-

бочими станциями может потребовать более вместитель-

ного здания, большего количества материалов и деталей в

системе, оборудования для транспортировки материалов,

не

говоря уж о дополнительном отоплении, освещении,

техническом обслуживании помещения и т.п.

Результаты моделирования предоставляют в распоря-

жение руководства немало полезной информации, с по-

мощью которой они

могут,

например, выяснить, какие

изменения

произойдут в системе, если автоматизировать

одно из рабочих мест. Сборочную линию можно промо-

делировать с помощью данных о таком автоматизирован-

ном

процессе и выяснить, оправданно ли подобное изме-

нение

с экономической точки зрения.

Моделирование

шшощью

электронных

таблиц

Как

мы уже не раз подчеркивали в этой книге, такие

электронные таблицы, как Microsoft

Excel,

оказывают

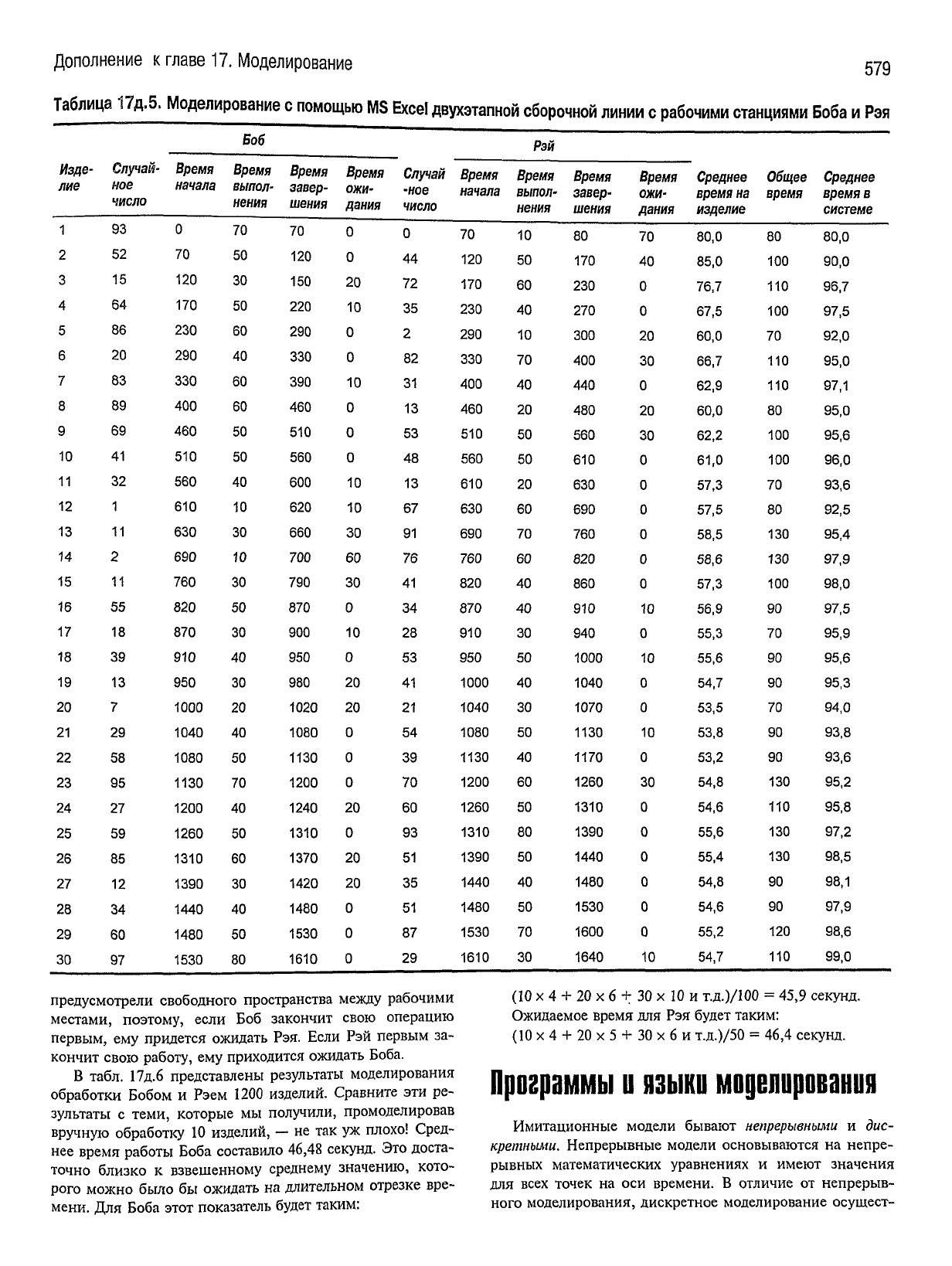
большую пользу при решении многих задач. В табл. 17д.5

показаны

результаты

моделирования с помощью Microsoft

Excel

двухэтапной сборочной линии с рабочими станция-

ми

Боба и Рэя. В соответствующей процедуре реализована

та же логика, которая использовалась нами при ручном

моделировании (см. табл.

17д.4).

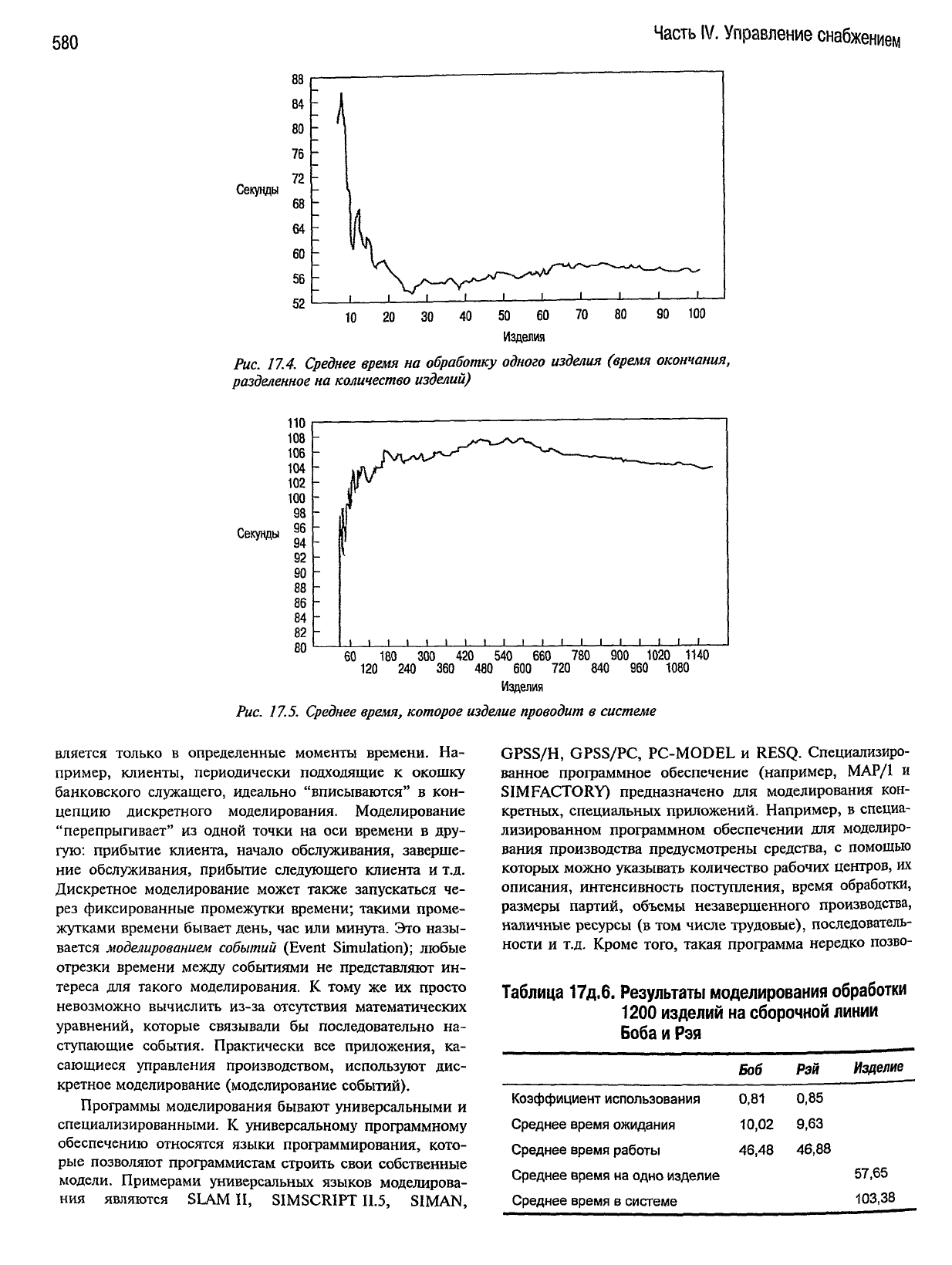
В целом процесс моделирования в

Excel

охватил 1200

итераций, что отражено на рис. 17.5 и в табл.

17д.6,

т.е. Рэй

обработал 1200 изделий. Имитационное моделирование

являясь

аналитическим инструментом, имеет преимущест-

во над количественными методами в том, что моделирова-

ние

отражает динамику,

тогда

как аналитические методы

фиксируют показатели, усредненные на длительном отрез-

ке времени. Как видно из рис. 17.4 и 17.5, в данном

случае

совершенно отчетлива переходная фаза. Может

даже

воз-

никнуть ряд вопросов в связи с долгосрочным функциони-

рованием такой сборочной линии, поскольку не заметно,

чтобы она в конце концов перешла в какое-либо устойчи-

вое состояние —

даже

после 1200 итераций (обработанных

изделий).

На рис. 17.4 показан

результат

прохождения че-

рез эту

двухэтапную

сборочную линию 100 изделий. Обра-

тите внимание на широкий разброс времени при обработке

первых изделий. Эти величины представляют собой сред-

нее время, которое

уходит

на обработку изделий. Речь в

данном

случае

идет о среднем по "нарастающему

итогу":

обработка первого изделия занимает время, выраженное

случайными числами; для

двух

изделий определяется сред-

нее время обработки изделия по

сумме

времени обработки

первого и второго изделий, разделенной на 2; для

трех

из-

делий — среднее время по

сумме

времени обработки пер-

вых

трех

изделий и т.д. Форма кривой в начале процесса

зависит только от потока случайных чисел и может отли-

чаться от показанной на рис. 17.4. Уверенным можно быть

лишь в том, что среднее время обработки в течение какого-

то периода времени

будет

значительно колебаться и, затем,

по

мере обработки изделий, эти колебания постепенно бу-

дут сглаживаться и установится относительно стабильное

среднее значение.

На

рис. 17.5 показано среднее время, проводимое из-

делиями в системе. В самом начале кривая отображает

нарастание количества времени, проводимого в системе.

Это можно было предвидеть, поскольку работа системы

начиналась "с нуля", и при передаче изделий от Боба к

Рэю

не возникает никаких задержек. Затем некоторым

изделиям, поступающим в систему, приходится ожидать

при

передаче с одной стадии обработки на

другую,

что

увеличивает "незавершенное производство". Задержки

последующих изделий приводят к постепенному накопле-

нию

времени ожидания. Однако через определенное вре-

мя

наступает фаза стабильности (если только производи-

тельность второй стадии не окажется меньше производи-

тельности первой стадии). В данном

случае

мы не

Дополнение

Таблица

17д.5.

Изде-

лие

Случай-

ное

число

главе 1

Моде;

Моделирование

Время

начала

120

170

230

290

330

400

460

510

560

610

630

690

760

820

870

910

950

1000

1040

1080

1130

1200

1260

1310

1390

1440

1480

1530

Боб

Время

выпол-

нения

|ирование

помощью

Время

завер-

шения

120

150

220

290

330

390

460

510

560

600

620

660

700

790

870

900

950

980

1020

1080

1130

1200

1240

1310

1370

1420

1480

1530

1610

Время

ожи-

дания

Excel

двухэтапной

сборочной

линии

рабочими

станциями

Случай

•ное

число

Время

начала

120

170

230

290

330

400

460

510

560

610

630

690

760

820

870

910

950

1000

1040

1080

1130

1200

1260

1310

1390

1440

1480

1530

1610

Рэй

Время

выпол-

нения

Время

завер-

шения

170

230

270

300

400

440

480

560

610

630

690

760

820

860

910

940

1000

1040

1070

1130

1170

1260

1310

1390

1440

1480

1530

1600

1640

Время

ожи-

дания

Среднее

время

на

изделие

80,0

85,0

76,7

67,5

60,0

66,7

62,9

60,0

62,2

61,0

57,3

57,5

58,5

58,6

57,3

56,9

55,3

55,6

54,7

53,5

53,8

53,2

54,8

54,6

55,6

55,4

54,8

54,6

55,2

54,7

Общее

время

100

110

100

110

100

130

100

130

110

130

120

110

579

Боба

и Рэя

Среднее

время

системе

80,0

90,0

96,7

97,5

92,0

95,0

97,1

95,0

95,6

96,0

93,6

92,5

95,4

97,9

98,0

97,5

95,9

95,6

95,3

94,0

93,8

93,6

95,2

95,8

97,2

98,5

98,1

97,9

98,6

99,0

предусмотрели свободного пространства

между

рабочими

местами, поэтому, если Боб закончит свою операцию

первым,

ему придется ожидать Рэя. Если Рэй первым за-

кончит

свою работу, ему приходится ожидать Боба.

В табл. 17д.6 представлены результаты моделирования

обработки Бобом и Рэем 1200 изделий. Сравните эти ре-

зультаты с теми, которые мы получили, промоделировав

вручную обработку 10 изделий, — не так уж плохо! Сред-

нее время работы Боба составило

46,48

секунд. Это доста-

точно близко к взвешенному среднему значению, кото-

рого можно было бы ожидать на длительном отрезке вре-

мени.

Для Боба этот показатель

будет

таким:

(10 х 4 + 20 х 6 + 30 х 10 и

т.д.)/100

= 45,9 секунд.

Ожидаемое время для Рэя

будет

таким:

(10х4 +

20х5

30х6и

т.д.)/50

= 46,4 секунд.

Программы

и языки моделирования

Имитационные

модели бывают

непрерывными

и дис-

кретными.

Непрерывные модели основываются на непре-

рывных математических уравнениях и имеют значения

для всех точек на оси времени. В отличие от непрерыв-

ного моделирования, дискретное моделирование осущест-

580

Часть

IV. Управление снабжением

Секунды

20 30 40

Изделия

Рис.

17.4.

Среднее

время на обработку

одного

изделия (время окончания,

разделенное

на количество изделий)

Секунды

1 1 1 1 1 Г

1 1 1

180 300 420 540 660 780 900 1020 1140

120

240 360 480 600 720 840 960 1080

Изделия

Рис.

17.5.

Среднее

время, которое изделие проводит в системе

вляется только

определенные моменты времени.

На-

пример,

клиенты, периодически подходящие

окошку

банковского служащего, идеально "вписываются"

кон-

цепцию

дискретного моделирования. Моделирование

"перепрыгивает"

из

одной точки

на оси

времени

в дру-

гую: прибытие клиента, начало обслуживания, заверше-

ние

обслуживания, прибытие

следующего

клиента

и т.д.

Дискретное моделирование может также запускаться

че-

рез фиксированные промежутки времени; такими проме-

жутками времени бывает день, час или минута. Это назы-

вается

моделированием

событий

(Event Simulation); любые

отрезки времени

между

событиями

не

представляют

ин-

тереса

для

такого моделирования.

тому

же их

просто

невозможно вычислить из-за отсутствия математических

уравнений, которые связывали

бы

последовательно

на-

ступающие события. Практически

все

приложения,

ка-

сающиеся управления производством, используют

дис-

кретное моделирование (моделирование событий).

Программы моделирования бывают универсальными

специализированными.

универсальному программному

обеспечению относятся языки программирования, кото-

рые позволяют программистам строить свои собственные

модели. Примерами универсальных языков моделирова-

ния

являются

SLAM

И, SIMSCRIPT 11.5, S1MAN,

GPSS/H,

GPSS/PC, PC-MODEL

RESQ. Специализиро-

ванное

программное обеспечение (например, МАР/1

SIMFACTORY) предназначено

для

моделирования

кон-

кретных, специальных приложений. Например,

специа-

лизированном

программном обеспечении

для

моделиро-

вания

производства предусмотрены

средства,

помощью

которых можно указывать количество рабочих центров, их

описания,

интенсивность поступления, время обработки,

размеры партий, объемы незавершенного производства,

наличные ресурсы (в том числе трудовые), последователь-

ности

и т.д.

Кроме того, такая программа нередко позво-

Таблица

17д.6.

Результаты моделирования обработки

1200 изделий на сборочной линии

Боба и Рэя

Коэффициент

использования

Среднее

время ожидания

Среднее

время работы

Среднее

время на одно изделие

Среднее

время

системе

Боб

0,81

10,02

46,48

Рэй

0,85

9,63

46,88

Изделие

57,65

103,38