Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Дополнение к главе 17. Моделирование

581

ляет аналитику наблюдать производственный процесс

анимационном

представлении

следить

по

ходу

модели-

рования

за

количественными показателями

потоками

системе. Данные собираются, анализируются

представ-

ляются

форме, наиболее подходящей

для

приложения

соответствующего типа.

Существует немало компьютерных программ модели-

рования,

предназначенных

для

выполнения

на

компьюте-

рах различных типов—

от

микрокомпьютеров

до

"мэйнфреймов"

(больших ЭВМ). Как

же из

столь внуши-

тельного перечня выбрать самую подходящую программу?

Прежде всего нужно понимать,

что

существуют

раз-

личные типы моделирования. Затем, внимательно изучив

программы, которые предлагает рынок, нужно найти

та-

кую, которая соответствует вашим конкретным потребно-

стям.

Пример успешного применения одной

из

коммер-

ческих программ приведен

во

врезке "Причины перепол-

нения

больниц удалось установить

ходе

модели-

рования".

Если

же

подходящей программы

не

удается

найти,

иногда

не так уж

сложно создать собственную

специализированную программу моделирования.

Тем бо-

лее,

что

такая программа

будет

полностью соответствовать

вашим

потребностям

и с ее

использованием

у вас

навер-

няка

не

возникнет проблем.

Systems Modeling Corporation проектирует программы модели-

рования

для

различных систем,

начиная

производственных

предприятий

заканчивая ресторанами быстрого питания.

Мо-

дели, разработанные

помощью

их

продуктов

—

SIMAN/Cinema

и Arena,

—

можно использовать для помощи инженерам

ме-

неджерам, пытающимся отыскать "узкие места"

другие

про-

блемы

уже существующих системах или рассчитать мощности

производственных потоков предлагаемых систем

(например,

завода, показанного на этом рисунке),

http://www.sm.com

последнее замечание, касающееся программ моде-

лирования:

хорошим средством моделирования являются

электронные

таблицы. Как

вы уже

заметили, двухэтапную

систему Боба

Рэя

мы

моделировали

предыдущем

раз-

деле

помощью электронных таблиц. Электронные

таб-

лицы

становятся

все

более "дружественными"

по

отно-

шению

пользователю,

в них

появляются

все

новые

воз-

можности (например, возможность генерирования

слу-

чайных чисел

возможность ставить вопросы типа

"а

что,

если..."). Простота применения электронных

таб-

лиц

для

моделирования может

лихвой компенсировать

любую

потребность

упрощении задачи, вызванную

же-

ланием

воспользоваться электронными таблицами.

Для расширения возможностей электронных таблиц

можно использовать программный продукт

@RISK,

рабо-

тающий

Microsoft Excel.

Эта

программа добавляет

электронным

таблицам множество полезных функций,

связанных

моделированием. Использование

@RISK

по-

зволяет автоматизировать извлечение случайных значений

из

любой указанной функции распределения, автомати-

зировать пересчет электронной таблицы

на

основе новых

случайных значений; кроме того,

эта

программа отобра-

жает выходные значения

статистику.

@RISK

упрощает

процесс построения

"прогона" имитационных моделей,

созданных

на

основе электронных таблиц

Желательные

характеристики моделирующих программ

Чтобы научиться работать

программами моделирова-

ния,

требуется определенное время. После того

как

поль-

зователь освоит какую-либо

из

этих программ,

он, как

правило,

очень неохотно переходит

работе

другой

программой. Поэтому

проблеме первого выбора нужно

подходить

со

всей ответственностью. Программа модели-

рования

должна отвечать следующим требованиям.

Она

должна предусматривать возможность использова-

ния

как

интерактивном режиме,

так и в

режиме авто-

матического выполнения,

т.е. от

начала

до

конца

без

вмешательства человека.

Она

должна быть "дружественной"

по

отношению

пользователю,

а ее

освоение

не

должно быть связано

чрезмерными усилиями.

Она

должна обеспечивать возможность создания

моду-

лей

последующего

их

объединения.

таком

случае

модули можно разрабатывать

по

отдельности,

не

затра-

гивая при этом

всю

остальную систему.

Она

должна давать возможность пользователям самим

писать

подключать собственные подпрограммы

— ни-

какая

программа моделирования

не в

состоянии обес-

печить все потребности пользователей.

Она

должна включать "строительные блоки"

со

встро-

енными

командами (например, статистический анализ

или

правила принятия решений относительно того,

куда

переходить дальше).

В ней

должно быть предусмотрено средство написания

макрокоманд,

например средство проектирования обра-

батывающих ячеек (Machining Cells).

7. В ней должно быть предусмотрено средство описания

ма-

териальных потоков. Производство связано

перемеще-

нием

материалов

людей;

программе должна быть пре-

дусмотрена возможность моделирования вагонеток, теле-

жек, грузоподъемных кранов, конвейеров

и т.д.

См.

работу

Wayne

Winston,

Simulation

Modeling Using

@RISK

(Belmont,

CA:

Wadsworth Publishing Company, 1996). Продукт

@RISK разработан компанией

(http://www.palisade.com).

Palisade

Corporation

582

Часть

IV. Управление снабжением

НОВАЦИЯ

Причины переполнения

вольниц

удалось установишь в коде моделироваш

Благодаря увеличению продолжительности жизни,

достигнутому

за

счет

улучшения качества медицинского

обслуживания

сочетании

переменами

демографи-

ческой

структуре

населения, больницы повсеместно

оказываются переполненными. Ограниченные

бюджеты

здравоохранения заставляют руководство больниц

ис-

кать нестандартные решения этой неожиданно возник-

шей проблемы. Однако особенностью

любых

нестан-

дартных решений является высокий риск, связанный

попытками

их

внедрения, поэтому эффективность

та-

ких решений желательно оценить

еще на

стадии проек-

тирования.

точки зрения затрат,

чем

раньше

будет

сделана оценка эффективности предлагаемого решения

(и

соответственно,

чем

раньше

это

решение

будет

при-

нято

или отвергнуто), тем лучше.

Лаборатория

Outpatient

Laboratory

при медицинском центре

Bay

Medical

Center,

как и

многие

другие

медицинские учреждения, испытывала серьезные трудности

обеспеченностью "производственными

мощностями".

дополнение

этим трудностям, руководство лаборатории затеяло реконструкцию. Впро-

чем,

эта

реконструкция, призванная повысить эффективность лаборатории, лишь добавила

им

проблем.

Одной

из

этих проблем стало переполнение.

начале

1992

года

Дейв Нэлл, главный инженер

(Management Engineer)

Bay

Medical

Center,

решил провести исследование, чтобы оценить несколько вари-

антов

сформулировать рекомендации

для

устранения "узких мест"

повышения пропускной способ-

ности

Outpatient

Laboratory.

Задача этого исследования заключалась

разработке

оценке разных спосо-

бов борьбы

переполнением

Outpatient

Laboratory.

Решение

Основной технологией, которой воспользовался Дейв

при

проведении этого исследования, было

ком-

пьютерное моделирование. Дейв

раньше неоднократно использовал

своей работе компьютерное

мо-

делирование

пришел

вьшоду,

что это

весьма эффективный способ разобраться

проблеме

оценить

возможные варианты

ее

решения.

На

основе дискуссий

менеджерами, отвечающими

за

работу

Outpatient

Laboratory,

Дейв построил

се-

тевую

модель,

которой отразил характеристики потока пациентов через лабораторию

в его

нынешнем

виде. Затем были собраны данные

времени, которое

требуется

пациентам

для

получения

тех или

иных

медицинских

услуг,

также

времени, которое

требуется

пациентам

для

перемещения

из

одной комна-

ты,

где им

оказывались соответствующие

услуги,

другую.

На

основании этой информации Дейв

по-

строил

базовую

компьютерную модель лаборатории.

Затем Дейв несколько видоизменил

эту

компьютерную модель

воспользовался

ею для

исследования

вопросов, касающихся

трех

способов решения проблемы переполнения

Outpatient

Laboratory.

a) изменение штатного расписания, которое должно было коснуться

не

только медицинского персона-

ла,

но и

административных работников;

b) использование

другой

клиники

качестве "шлюза", открывающегося

при

возникновении перепол-

нения;

c) возможная реконструкция "производственных мощностей" самой лаборатории.

Дополнение к главе 17. Моделирование

583

Что касается изменения штатного расписания, то компьютерное моделирование позволило устано-

вить, что существовавший на тот момент штат медицинских работников был близок к оптимальному. Что

же касается административного персонала, то Дейв лришел к

выводу,

что его вполне можно сократить

без

ущерба

для обслуживания пациентов. Однако проблемы с персоналом не представлялись самыми

главными. Учитывая возможность использования (при переполнении) "производственных мощностей"

другой

лаборатории, можно было рассчитывать на значительное повышение пропускной способности

Outpatient

Laboratory

— правда, для этого еще требовалось уговорить пациентов воспользоваться

услугами

другой

лаборатории. Несмотря на то, что моделирование ничего не говорило о том, как

следует

уговари-

вать пациентов, оно позволило Дейву выполнить количественную оценку преимуществ, связанных с по-

вышением

коэффициента использования такой альтернативной лаборатории на 5%, 10% и т.д. Что же

касается варианта реконструкции

действующих

"производственных мощностей"

Outpatient

Laboratory,

то

Дейв пришел к

выводу,

что

даже

случае

относительно небольшой их реконструкции и внесения опре-

деленных процедурных изменений можно добиться значительного повышения пропускной способности

Outpatient

Laboratory.

Повышение пропускной способности, конечно же, подразумевало и повышение ка-

чества обслуживания пациентов.

Преимущества

Разумеется, никто заранее не мог бы точно предсказать

результаты

тех или иных способов решения

проблемы переполнения лаборатории

Outpatient

Laboratory

при медицинском центре Bay

Medical

Center,

опираясь

лишь на собственную интуицию. Результаты анализа моделирования и сделанные из этого вы-

воды помогли Дейву оценить относительные достоинства и недостатки каждого из альтернативных вари-

антов,

а также предсказать их влияние на эффективность работы лаборатории. Сделав незначительные

капиталовложения в виде рабочего времени, затраченного Дейвом на моделирование, руководство Bay

Medical

Center

смогло принять обоснованные решения с

учетом

возможных затрат и потенциальных вы-

год. Принятые решения оказались правильными и своевременными. Они позволили сэкономить немало

денег и повысить качество обслуживания пациентов.

Источник.

Micro

Analysis

and Design Simulation Software, Inc., Boulder,

CO.

8. В ней должна быть предусмотрена возможность вывода

стандартной статистики, например длительности цикла,

коэффициента

использования и времени ожидания.

9. Она должна допускать множество вариантов анализа

данных (как для

входных,

так и для выходных данных).

10. В ней должна быть предусмотрена возможность анима-

ции,

позволяющая отображать в графическом виде по-

ток

продукции через систему.

11.

В ней должна быть предусмотрена возможность инте-

рактивной

отладки модели, в

ходе

которой пользователь

мог бы отслеживать потоки в модели и легко отыски-

вать ошибки

Преимущества и недостатки

имитационного

моделирования

Ниже

приводится перечень доводов в пользу примене-

ния

имитационного моделирования, а также случаев, ко-

Wali

Haider and Jerry Banks, "Simulation Software Products for

Analyzing

Manufacturing Systems",

Industrial

Engineering,

July 1986,

98-103.

гда его применение противопоказано (хотя мы сразу же

должны отметить, что этот перечень ни в коем

случае

нельзя

считать исчерпывающим — скорее мы перечисля-

ем общеизвестные преимущества и недостатки имитаци-

онного

моделирования).

Преимущества

1. Разработка имитационной модели системы

зачастую

по-

зволяет

лучше

понять реальную систему.

2. В

ходе

моделирования возможно "сжатие" времени: годы

практической

эксплуатации реальной системы можно

промоделировать в течение нескольких секунд или минут.

3. Моделирование не

требует

прерывания текущей дея-

тельности реальной системы.

4. Имитационные модели носят намного более общий ха-

рактер,

чем математические модели; их можно исполь-

зовать в тех

случаях,

когда для проведения стандартного

математического анализа нет надлежащих условий.

5. Моделирование можно использовать в качестве средства

обучения персонала работе с реальной системой.

6. Моделирование обеспечивает более реалистичное вос-

произведение системы, чем математический анализ.

7. Моделирование можно использовать для анализа пере-

ходных

процессов,

тогда

как математические модели для

этой

цели не подходят.

584

Часть

IV. Управление

снабжением

8. В настоящее время разработано множество стандартизо-

ванных моделей, охватывающих широкий спектр объек-

тов реального мира.

9. Имитационное моделирование

отвечает

на вопросы ти-

па

"а что, если...".

Недостатки

1. Несмотря на то, что на разработку имитационной моде-

ли

системы может уйти довольно много времени и тру-

да, нет никакой гарантии, что модель позволит получить

ответы на интересующие нас вопросы.

2. Нет никакого способа доказать, что работа модели пол-

ностью

соответствует

работе реальной системы. Моде-

лирование

связано с многочисленными повторениями

последовательностей, которые основываются на генера-

ции

случайных чисел, имитирующих наступление тех

или

иных событий. Явно стабильная система может —

при

неблагоприятном сочетании событий — "пойти

вразнос"

(хотя это и весьма маловероятно).

3. В зависимости от системы, которую мы хотим модели-

ровать, построение модели может занять от одного часа

до 100 человеко-лет. Моделирование сложных систем

может оказаться весьма дорогостоящей затеей и занять

немало времени.

4. Моделирование может быть менее точным, чем матема-

тический

анализ, поскольку — подчеркнем еще раз — в

его основу положена генерация случайных чисел. Если

реальную систему можно представить математической

моделью, предпочтение

следует

отдать

именно такому

способу моделирования.

5. Для "прогона" сложных моделей

требуется

довольно

значительное компьютерное время.

6. Для метода имитационного моделирования по-

прежнему характерно недостаточное использование

стандартизованных

подходов

(хотя некоторый прогресс

преодолении этого недостатка уже намечается). В ре-

зультате

модели одной и той же реальной системы, по-

строенные разными аналитиками,

могут

иметь мало

общего

между

собой.

Резюме

Можно

утверждать,

что все, что поддается математиче-

скому анализу, можно описать с помощью имитационных

моделей. Однако моделирование далеко не

всегда

являет-

ся

идеальным решением проблемы. Если интересующую

нас

проблему можно решить математическими методами,

предпочтение

следует

отдать

именно им, поскольку это

займет меньше времени и обойдется дешевле. Кроме то-

го,

очевидным достоинством математического анализа яв-

ляется доказуемость, и вопрос заключается лишь в том,

действительно ли данная математическая модель адекват-

но

отображает реальную систему.

В то же время о моделировании нельзя сказать ничего

определенного: для построения моделей и выдвижения

допущений относительно моделируемой системы практи-

чески

нет никаких границ. Повышение возможностей

17 457

03 704

56 970

55 503

47 019

84 828

36 458

05 752

компьютеров (быстродействие и объем памяти)

сущест-

венно

расширяет спектр объектов реального мира, кото-

рые можно описывать имитационными моделями.

Появ-

ление все новых и более совершенных языков и программ

моделирования — как универсальных (SIMAN, SLAM),

так

и специализированных программ (МАР/1,

SIMFACTORY, Optima!) — позволяет надеяться на суще-

ственное облегчение всего процесса создания имитацион-

ных моделей.

Задачи с решениями

Задача

Воспользовавшись хорошо известным статистическим

примером

имитационного моделирования, разработать

имитационную модель процесса вытаскивания шаров из

урны, если в урне находится 100 шаров, 10% из которых

зеленые, 40% — красные, а 50% — пятнистые. Каждый

раз,

когда из урны вытаскивается шар и фиксируется его

цвет, он заменяется. При желании можно воспользовать-

ся

приведенными ниже случайными числами.

Промоделируйте вытаскивание 10 шаров из урны. По-

кажите, какие числа

БЫ

использовали.

26 768

954 83125 08

021

613

95 457

95 276

Решение

Назначьте шарам случайные числа, которые

будут

со-

ответствовать процентному соотношению шаров в урне.

Случайное

число

зеленых

шаров 00-09

красных шаров

10-49

пятнистых шаров 50—99

Существует

много возможных ответов, которые зави-

сят от того, как присваивались случайные числа и какие

именно

числа из прилагаемого списка использованы.

Если

последовательность случайных чисел соответст-

вует

той, которая указана выше, и если использовать две

первые цифры из каждого числа, мы получим:

Цвет

шара

Красный

Зеленый

Пятнистый

Среди вытащенных 10 шаров оказался 1 зеленый, 3

красных и 6 пятнистых шаров — неплохая оценка, если

учесть

незначительную величину выборки (10).

Случайное

число

Цвет

шара

Красный

Пятнистый

Случай

число

Дополнение

главе 17. Моделирование

585

Клиника

в маленьком городке

каждую

неделю получа-

ет партию свежей плазмы из центрального банка крови.

Конкретная

поставка зависит от спроса со стороны

других

клиник

и больниц в данном регионе, однако колеблется

от

четырех

до девяти пинт крови наиболее широко ис-

пользуемого типа — типа 0. Число пациентов в неделю,

которым

требуется

эта кровь, колеблется от нуля до четы-

рех, причем каждому пациенту может потребоваться от

одной

до

четырех

пинт. Каким может оказаться избыток

или

нехватка крови (выраженные в пинтах) на протяже-

нии

шестинедельного периода при указанных ниже объе-

мах поставок, распределении пациентов и потребности в

крови

на одного пациента? Для получения ответа вос-

пользуйтесь моделированием. Рассмотрите случай, когда

плазму можно хранить в течение длительного времени, но

данный момент запас плазмы полностью

отсутствует.

Объемы

поставок

Пинт

неделю

Вероят-

ность

0,15

0,20

0,25

0,15

0,10

Распределение

пациентов

Пациентов

неделю,

которым

требуется

кровь

Вероят-

ность

0,25

0,30

0,15

0,05

Потребность

расчете

на

одного пациента

Пинты Вероят-

ность

1 0,40

0,30

0,20

0,10

Решение

Прежде всего выбираем последовательность случайных

чисел, затем выполняем моделирование.

Пинты

Кровь

Поставки

Вероятность

0,15

0,20

0,25

0,15

0,10

Количество пациентов

Вероятность

0,25

0,30

0,15

0,05

Случайное число

00-14

15-34

35-59

60-74

75-89

90-99

Случайное число

00-24

25-49

50-79

80-94

95-99

Потребность

расчете

на

одного пациента

Пинты

Вероятность

0,40

0,30

0,20

0,10

Случайное число

00-39

40-69

70-89

90-99

(Далее см. таблицу на следующей странице).

В конце шести недель в клинике остается 14 пинт

крови.

Вопросы

для контроля о обсуждения

1. Почему моделирование иногда называют "последним

средством"?

2. Какую роль в моделировании играет испытание стати-

стических гипотез?

3. Что

служит

признаком того, что имитационная модель

верна?

4. Обязательно ли использовать компьютер, чтобы в ре-

зультате

моделирования получить достоверную

инфор-

мацию? Поясните свой

ответ.

5. Какие методы используются для наращивания времени

модели? Поясните принцип их действия.

6. Каковы "за" и "против" начала моделирования с

"пустой" системы? А с системой в состоянии равновесия?

7. Поясните разницу

между

известными математическими

распределениями и эмпирическими распределениями.

Какая

информация потребуется для выполнения моде-

лирования,

если воспользоваться одним из известных

математических распределений?

8. Какую роль в моделировании играет длительность

"прогона"? Можно ли сказать, что "прогон", включаю-

щий

100 наблюдений, в два раза достовернее "прогона"

из

50 наблюдений? Поясните свой

ответ.

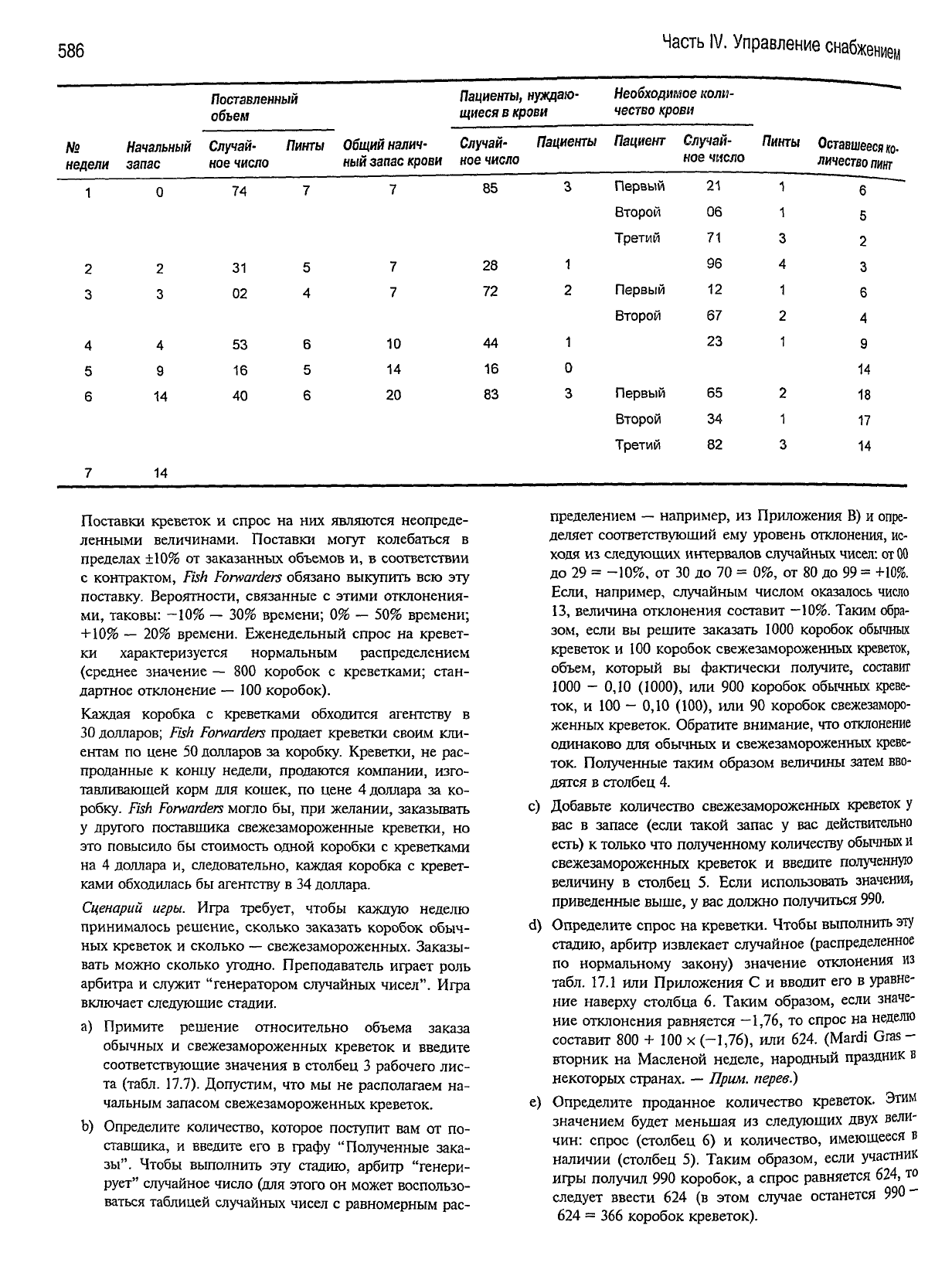
Задачи

Моделирование

аудитории:

рыбное

экспедиционное

агентство

Это — игровое упражнение, позволяющее проверить

умение участников устанавливать правила формирования

заказов

для пополнения материальных запасов на протя-

жении

10-недельного периода планирования. Макси-

мальную прибыль в конце определяет победитель.

Рыбное

экспедиционное агентство

(Fish

Forwarders)

по-

ставляет свежие креветки различным потребителям в

районе

Нового Орлеана. В начале каждой недели агент-

ство размещает заказы на поставку коробок с креветка-

ми

у представителей рыболовецких флотилий, чтобы

удовлетворить спрос своих клиентов на этот продукт,

начиная

с середины той же недели. Креветки поставля-

ются сначала

агентству

Fish

Forwarders,

а затем — в кон-

це недели — потребителям.

586

Часть

IV. Управление снабжением

№

недели

Начальный

запас

Поставленный

объем

Случай-

ное число

Пинты

Общий налич-

ный запас крови

Пациенты, нуждаю-

щиеся

крови

Случай-

ное число

Пациенты

Необходимое коли-

чество крови

Пациент

Первый

Второй

Третий

Первый

Второй

Первый

Второй

Третий

Случай-

ное число

Пинты

Оставшееся

ко-

личество

пинт

Поставки

креветок

спрос

на них

являются неопреде-

ленными

величинами. Поставки

могут

колебаться

пределах

±10%

от

заказанных объемов

и, в

соответствии

контрактом,

Fish

Forwarders

обязано выкупить

всю эту

поставку. Вероятности, связанные

этими отклонения-

ми,

таковы: —10%

— 30%

времени;

0% — 50%

времени;

+10%

— 20%

времени. Еженедельный спрос

на

кревет-

ки

характеризуется нормальным распределением

(среднее значение

— 800

коробок

креветками; стан-

дартное отклонение

— 100

коробок).

Каждая коробка

креветками обходится агентству

30 долларов;

Fish

Forwarders

продает креветки своим

кли-

ентам

по

цене

долларов

за

коробку. Креветки,

не рас-

проданные

концу недели, продаются компании, изго-

тавливающей корм

для

кошек,

по

цене

доллара

за ко-

робку.

Fish

Forwarders

могло

бы, при

желании, заказывать

другого

поставщика свежезамороженные креветки,

но

это

повысило

бы

стоимость одной коробки

креветками

на

доллара

и,

следовательно, каждая коробка

кревет-

ками

обходилась

бы

агентству

в 34

доллара.

Сценарий

игры.

Игра

требует,

чтобы каждую неделю

принималось

решение, сколько заказать коробок обыч-

ных креветок

сколько

—

свежезамороженных. Заказы-

вать можно сколько угодно. Преподаватель играет роль

арбитра

служит "генератором случайных чисел". Игра

включает следующие стадии.

a) Примите решение относительно объема заказа

обычных

свежезамороженных креветок

введите

соответствующие значения

столбец

рабочего лис-

та (табл. 17.7). Допустим,

что мы не

располагаем

на-

чальным запасом свежезамороженных креветок.

b) Определите количество, которое поступит

вам от по-

ставщика,

введите

его в

графу "Полученные зака-

зы".

Чтобы выполнить

эту

стадию, арбитр "генери-

рует"

случайное число (для этого

он

может воспользо-

ваться таблицей случайных чисел

равномерным

рас-

пределением

—

например,

из

Приложения

В) и

опре-

деляет соответствующий

ему

уровень отклонения, ис-

ходя

из

следующих интервалов случайных чисел:

от 00

до

29 = -10%, от 30 до 70 = 0%, от 80 до

99 =

+10%.

Если,

например, случайным числом оказалось число

13,

величина отклонения составит —10%. Таким обра-

зом,

если

вы

решите заказать

1000

коробок обычных

креветок

и 100

коробок свежезамороженных креветок,

объем, который

вы

фактически получите, составит

1000

- 0,10

(1000),

или 900

коробок обычных креве-

ток,

и 100 - 0,10

(100),

или 90

коробок свежезаморо-

женных креветок. Обратите внимание,

что

отклонение

одинаково

для

обычных

свежезамороженных креве-

ток.

Полученные таким образом величины затем вво-

дятся

столбец

c) Добавьте количество свежезамороженных креветок

вас

запасе (если такой запас

у вас

действительно

есть)

только

что

полученному количеству обычных

свежезамороженных креветок

введите полученную

величину

столбец

Если использовать значения,

приведенные выше,

вас должно получиться

990.

d) Определите спрос

на

креветки. Чтобы выполнить эту

стадию, арбитр извлекает случайное (распределенное

по

нормальному закону) значение отклонения

из

табл.

17.1 или

Приложения

С и

вводит

его в

уравне-

ние

наверху столбца

Таким образом, если значе-

ние

отклонения равняется

-1,76,

то

спрос

на

неделю

составит

800 + 100 х

(-1,76),

или 624.

(Mardi Gras

вторник

на

Масленой неделе, народный праздник

некоторых странах.

—

Прим.

перев.)

e) Определите проданное количество креветок. Этим

значением

будет

меньшая

из

следующих

двух

вели-

чин:

спрос (столбец

6) и

количество, имеющееся

наличии

(столбец

5).

Таким образом, если участник

игры получил

990

коробок,

спрос равняется

624, то

следует

ввести

624 (в

этом

случае

останется

990 -

624

= 366

коробок креветок).

Дополнение

главе

17.

Моделирование

587

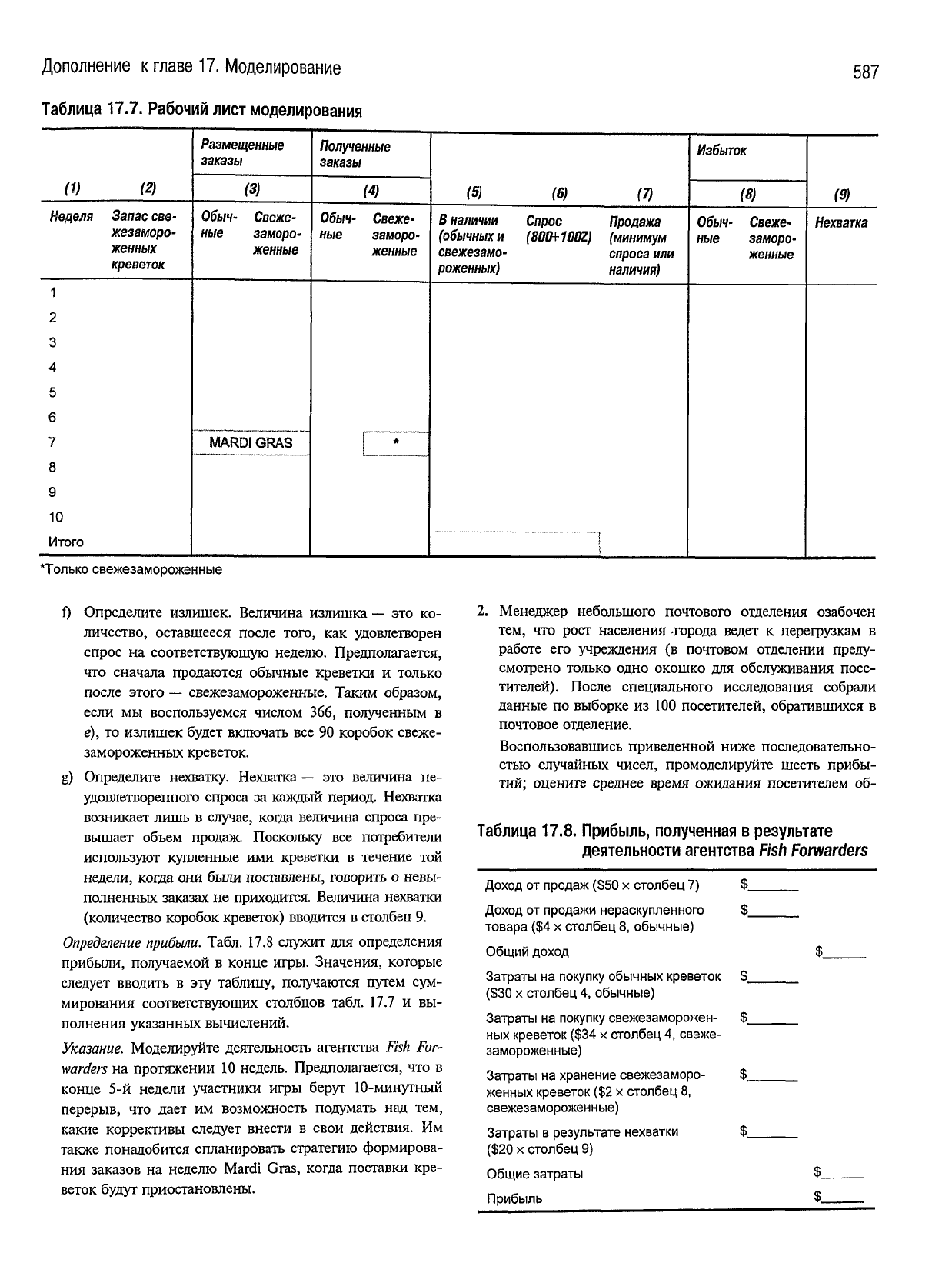
Таблица

17.7.

Рабочий лист моделирования

(1)

Неделя

Итого

(2)

Запас

све-

жезаморо-

женных

креветок

Размещенные

заказы

(3)

Обыч-

Свеже-

ные заморо-

женные

MARDIGRAS

Полученные

заказы

(4)

Обыч-

Свеже-

ные заморо-

женные

(5)

В наличии

(обычных

свежезамо-

роженных)

(6)

Спрос

(80IH100Z)

(7)

Продажа

(минимум

спроса

или

наличия)

Избыток

(8)

Обыч-

Свеже-

ные заморо-

женные

(9)

Нехватка

Только

свежезамороженные

f) Определите излишек. Величина излишка — это ко-

личество, оставшееся после того, как удовлетворен

спрос на соответствующую неделю. Предполагается,

что сначала продаются обычные креветки и только

после этого — свежезамороженные. Таким образом,

если мы воспользуемся числом 366, полученным в

е),

то излишек

будет

включать все 90 коробок свеже-

замороженных креветок.

g) Определите нехватку. Нехватка — это величина не-

удовлетворенного спроса за каждый период. Нехватка

возникает

лишь в случае, когда величина спроса пре-

вышает объем продаж. Поскольку все потребители

используют купленные ими креветки в течение той

недели, когда они были поставлены, говорить о невы-

полненных

заказах не приходится. Величина нехватки

(количество коробок креветок) вводится в столбец 9.

Определение

прибыли.

Табл. 17.8 служит для определения

прибыли,

получаемой в конце игры. Значения, которые

следует

вводить в эту таблицу, получаются путем сум-

мирования

соответствующих столбцов табл. 17.7 и вы-

полнения

указанных вычислений.

Указание.

Моделируйте деятельность агентства

Fish

For-

warders

на протяжении 10 недель. Предполагается, что в

конце

5-й недели участники игры

берут

10-минутный

перерыв,

что

дает

им возможность подумать над тем,

какие

коррективы

следует

внести в свои действия. Им

также понадобится спланировать стратегию формирова-

ния

заказов на неделю Mardi Gras, когда поставки кре-

веток

будут

приостановлены.

2. Менеджер небольшого почтового отделения озабочен

тем, что рост населения -города

ведет

к перегрузкам в

работе его учреждения (в почтовом отделении преду-

смотрено только одно окошко для обслуживания посе-

тителей). После специального исследования собрали

данные по выборке из 100 посетителей, обратившихся в

почтовое отделение.

Воспользовавшись приведенной ниже последовательно-

стью случайных чисел, промоделируйте шесть прибы-

тий;

оцените среднее время ожидания посетителем об-

Таблица

17.8.

Прибыль,

полученная

результате

деятельности агентства

Fish

Forwarders

Доход

от

продаж ($50

столбец

Доход

от

продажи нераскупленного

товара ($4

столбец

обычные)

Общий доход

Затраты

на

покупку

обычных

креветок

($30

столбец

обычные)

Затраты

на

покупку свежезаморожен-

ных креветок ($34

столбец

свеже-

замороженные)

Затраты

на

хранение свежезаморо-

женных креветок ($2

столбец

свежезамороженные)

Затраты

результате нехватки

($20

столбец

Общие затраты

Прибыль

588

Часть

IV. Управление снабжением

Время между

прибытием

посетителей

(минуты)

Частота

Итого:

100

Время обслуживания

(минуты)

Частота

1,0

1,5

2,0

2,5

3,0

3,5

Итого:

100

служивания и среднее время простоя служащих почто-

вого отделения.

Случайные числа: 08, 74, 24, 34, 45, 86, 31, 32, 45, 21, 10,

67, 60, 17, 60, 87, 74, 96.

3. К Томасу Магнусу, частному детективу, обратился по-

тенциальный

клиент из города Камало (остров Моло-

каи).

Клиент обратился вовремя, поскольку Магнус ока-

зался "на мели" с последними 10 долларами в кармане.

Подписание

договора, однако, обусловлено прибытием

Магнуса к клиенту в Камало в течение ближайших

восьми часов. Магнус в настоящее время находится в

городе Кипахулу (остров Мауи) и в его распоряжении

есть три способа добраться до Камало:

a) добраться на машине до деревушки Хонокахуа, а за-

тем на шлюпке перебраться в Камало;

b) добраться до Хонокахуа, а затем, преодолев вплавь

10 миль пролива Паилоло, оказаться в Камало;

c) добраться на машине до городка Хана и попросить

своего

друга

Т.С. перебросить его вертолетом в Ка-

мало.

Если

выбрать вариант а), то время поездки на машине

до Хонокахуа приведено в "Распределении 1". Оказав-

шись

в Хонокахуа, Магнусу придется договариваться с

местными жителями. Переговоры придется вести с не-

сколькими

людьми, и, если Магнус приступит к ним,

перебираться через пролив вплавь

будет

уже поздно.

Суть переговоров заключается в том, сколько Магнус

должен уплатить каждому из

трех

фебцов на шлюпке

Время проведения переговоров, оплата

услуг

команды

шлюпки

и время шлюпки в пути отображены в

"Распределении 3", "Распределении 4" и "Распреде-

лении

5" соответственно. Можно допустить, что каждо-

му члену команды шлюпки

будет

выплачена одна и та

же сумма. Если общая сумма оплаты

услуг

команды

шлюпки

превысит 10 долларов, можно считать, что

Магнусу не повезло — время поездки в таком

случае

стремится к бесконечности.

Время поездки на машине до Хонокахуа и время пре-

одоления

вплавь пролива Паилоло для варианта

Ь)

при-

ведены в "Распределении 1" и "Распределении 6".

Время поездки на машине до городка Хана для вариан-

та с) приведено в "Распределении 2". Однако Т.С. нахо-

дится в аэропорту лишь 10% времени. Если Т.С. нет в

аэропорту, Магнусу придется ждать, пока он появится

там. Время ожидания Магнусом своего приятеля Т.С.

задано "Распределением 8". Т.С, несмотря на свои са-

мые теплые

чувства

к Магнусу, может отказаться лететь

Камало за имеющиеся у Магнуса 10 долларов; вероят-

ность такого отказа, по прикидкам Магнуса, составляет

30%. Время ведения переговоров с Т.С. можно считать

равным

нулю. Если Т.С. отказывается, Магнус добира-

ется на машине до Хонокахуа через Кипахулу, а затем

вплавь перебирается через пролив Паилоло. Время вер-

толета в пути задано "Распределением 7".

Промоделируйте

дважды

каждый из

трех

способов доб-

раться до Камало и, основываясь на

результатах

моде-

лирования,

вычислите среднее время в пути для каждого

из

этих вариантов. Воспользуйтесь приведенной ниже

последовательностью случайных чисел (именно в том

порядке,

в каком они указаны, и не пропуская ни од-

ного из них).

Случайные числа: 7, 3, 0, 4, 0, 5, 3, 5, 6, 1, 6, 6, 4,

8,4,9,

0, 7, 7, 1, 7, 0, 6, 8, 8, 7, 9, 0, 1, 2, 9, 7, 3, 2, 3, 8, 6, 0, 6,

0, 5, 9, 7, 9, 6, 4, 7, 2, 8, 7, 8, 1, 7, 0, 5

Распределение

Время поездки

на

автомобиле от

Кипахулу до Хонокахуа (часы)

Время

Вероятность

Случайное

число

1,5

0,2

0,6

0,2

0-1

2-7

8-9

Распределение

Время поездки на автомобиле

от

Кипахулу до городка Хана

обратно (часы)

Время

0,5

1,5

Вероятность

0,2

0,7

0,1

Случайное

число

0-1

2-8

Дополнение

главе 17. Моделирование

Распределение

Время проведения переговоров

(часы)

Вероятность

Случайное

число

1,5

2,5

0,2

0,3

0,2

0-1

2-4

5-7

8-9

Распределение

Оплата

Распределение

время

Распределение

Время

Распределение

время

1,5

Распределение

время

Оплата услуг одного члена команды

шлюпки

Вероятность

Случайное

число

0,3

0-2

0,3

3-5

0,4

6-9

Время,

чтобы

добраться

шлюпке

от Хонокахуа до Камало (часы)

Вероятность

Случайное

число

0,1

0,5

1-5

0,4

6-9

Время,

чтобы

перебраться

вплавь

от

Хонокахуа до Камало (часы)

Вероятность

Случайное

число

0,2

0-1

0,6

2-7

0,2

8-9

Время перелета от Хана до Камало

(часы)

Вероятность

Случайное

число

0,1

0,7

1-7

0,2

8-9

Время ожидания, проведенное Маг-

нусом в аэропорту(часы)

Вероятность

Случайное

число

0,1

0,2

0,4

0,3

1-2

3-6

7-9

589

4. Станки на предприятии периодически

выходят

из строя в

соответствии с приведенным ниже распределением вре-

мени

между

поломками. Время, которое

требуется

одно-

му рабочему-ремонтнику на полное обслуживание одного

станка, задается распределением времени обслуживания.

Время между поломками

Р(Х)

Случайное

число

(часы)

0,5

1,0

1,5

2,0

3,0

4,0

время

обслуживания

(часы)

0,5

1,0

2,0

3,0

4,0

5,0

0,30

0,22

0,16

0,10

0,14

0,08

Итого:

1,00

0,25

0,20

0,25

0,15

0,10

0,05

Итого:

1,00

0-29

30-51

52-67

68-77

78-91

92-99

Случайное

число

0-24

25-44

45-69

70-84

85-94

95-99

Промоделируйте поломки этих пяти станков. Вычисли-

те среднее время ремонта станка при наличии

двух

ра-

бочих-ремонтников и приведенной ниже последова-

тельности случайных чисел. (Оба рабочих-ремонтника

не

могут

чинить одновременно один и тот же станок.)

Случайные числа: 30, 81, 02, 91, 51, 08, 28, 44, 86, 84, 29,

08, 37, 34, 99

5. Дженнифер Джоунз — хозяйка небольшого кондитер-

ского магазина; она же единственная там работает. Был

проведен хронометраж времени

между

появлениями по-

купателей в магазине и временем, которое

требуется

г-

же Джоунз на обслуживание каждого покупателя. Вы-

борка из 100 покупателей

дала

следующие

результаты.

время между

прибытиями

(минуты)

Количество

наблюдений

590

Часть

IV.

Управление снабжением

Время обслуживания

(минуты)

Количество

наблюдений

Промоделируйте эту систему (т.е. все прибытия и об-

служивание) в

случае

последовательного прибытия и

обслуживания 10 покупателей.

Сколько

времени в среднем проводит покупатель в этой

системе? Для получения случайных чисел воспользуй-

тесь Приложением В.

6. В распоряжении профессионального тренера по амери-

канскому

футболу есть шесть атакующих защитников

(Running Backs). Тренер

хотел

бы оценить влияние воз-

можных травм игроков на имеющийся у него резерв

защитников.

Незначительная травма заставляет игрока

выйти из игры и пропустить лишь следующий матч.

Серьезная

травма заставляет игрока пропустить все мат-

чи

до конца сезона. Вероятность получения игроком в

ходе

матча серьезной травмы равняется 0,05. За игру

случается не больше одной серьезной травмы. Распре-

деление вероятностей незначительных травм в течение

одной

игры приведено в следующей таблице.

Количество

травм

Вероятность

0,2

0,5

0,22

0,05

0,025

0,005

Итого:

1,000

Сложилось впечатление, что игроки получают травмы со-

вершенно

случайно и в их распределении на протяжении

сезона

не наблюдается какой-либо отчетливо выраженной

закономерности.

В течение сезона проводится 10 матчей.

Воспользовавшись приведенной ниже последовательно-

стью случайных чисел, промоделируйте флуктуации ре-

зерва атакующих защитников, который есть в распоря-

жении

тренера, на весь сезон. Предполагается, что на

протяжении

сезона тренер не может включать в состав

команды

дополнительных атакующих защитников.

Случайные числа: 044, 392, 898, 615, 986, 959, 558, 353,

577, 866, 305, 813, 024, 189, 878, 023, 285, 442, 862, 848,

060, 131, 963, 874, 805, 105, 452.

7. На предприятии

Tucson

Mills

часто случаются незначи-

тельные поломки станков. Возникновение поломок и

время обслуживания, связанное с ремонтом станков

имеют случайное распределение. Руководство предпри-

ятия

пытается минимизировать затраты, связанные с

поломками

станков. Стоимость одного часа простоя

станков

составляет 40 долларов. Заработная плата рабо-

чих-ремонтников равна 12 долларов в час. Предвари-

тельное исследование позволило получить следующие

данные о промежутках времени

между

последователь-

ными

поломками и соответствующим временем обслу-

живания.

Относительная

частота

поломок

станков

Время

меаду

4 5 6 7 8 9

поломками

(в

минутах)

Относительная

частота

0,10

0,30 0,25 0,20 0,10 0,05

Относительная

частота

времени обслуживания

Время

обслужива-

4 5 6 7 8

ния

(в

минутах)

Относительная

частота

0,10

0,40 0,20 0,15 0,10 0,05

Выполните моделирование 30 поломок при

двух

усло-

виях — при наличии одного рабочего-ремонтника, при

наличии

двух

рабочих-ремонтников.

Чтобы определить время

между

поломками, воспользуй-

тесь приведенной ниже последовательностью случайных

чисел.

Случайные числа: 85, 16, 65, 76, 93, 99, 65, 70, 58, 44, 02,

85,

01, 97, 63, 52, 53, 11, 62, 28, 84, 82, 27, 20, 39, 70, 26,

21,41,81.

Чтобы определить время обслуживания, воспользуйтесь

приведенной

ниже последовательностью случайных чи-

сел.

Случайные числа: 68, 26, 85, 11, 16, 26, 95, 67, 97, 73, 75,

64, 26, 45, 01, 87, 20, 01, 19, 36, 69, 89, 81, 81, 02, 05, 10,

51,

24, 36.

a) Воспользовавшись результатами моделирования, вы-

числите

(1) суммарное время простоя рабочих-ремонтников

при

каждом из заданных условий;

(2) суммарную задержку, вызванную ожиданием ра-

бочего-ремонтника, который должен приступить

устранению поломки.

b) Укажите подход, обеспечивающий наименьшие за-

траты.

8. Сервисная станция

Jethro

располагает только одной за-

правочной

колонкой. Поскольку все автомобилисты ок-

руга

Корнфилд водят большие автомобили, на станции

есть место лишь для

трех

таких автомобилей (в том чис-

ле и автомобиля у заправочной

колонки).

Автомобили-

сты, подъезжающие к станции в тот момент, когда там