Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Приложение

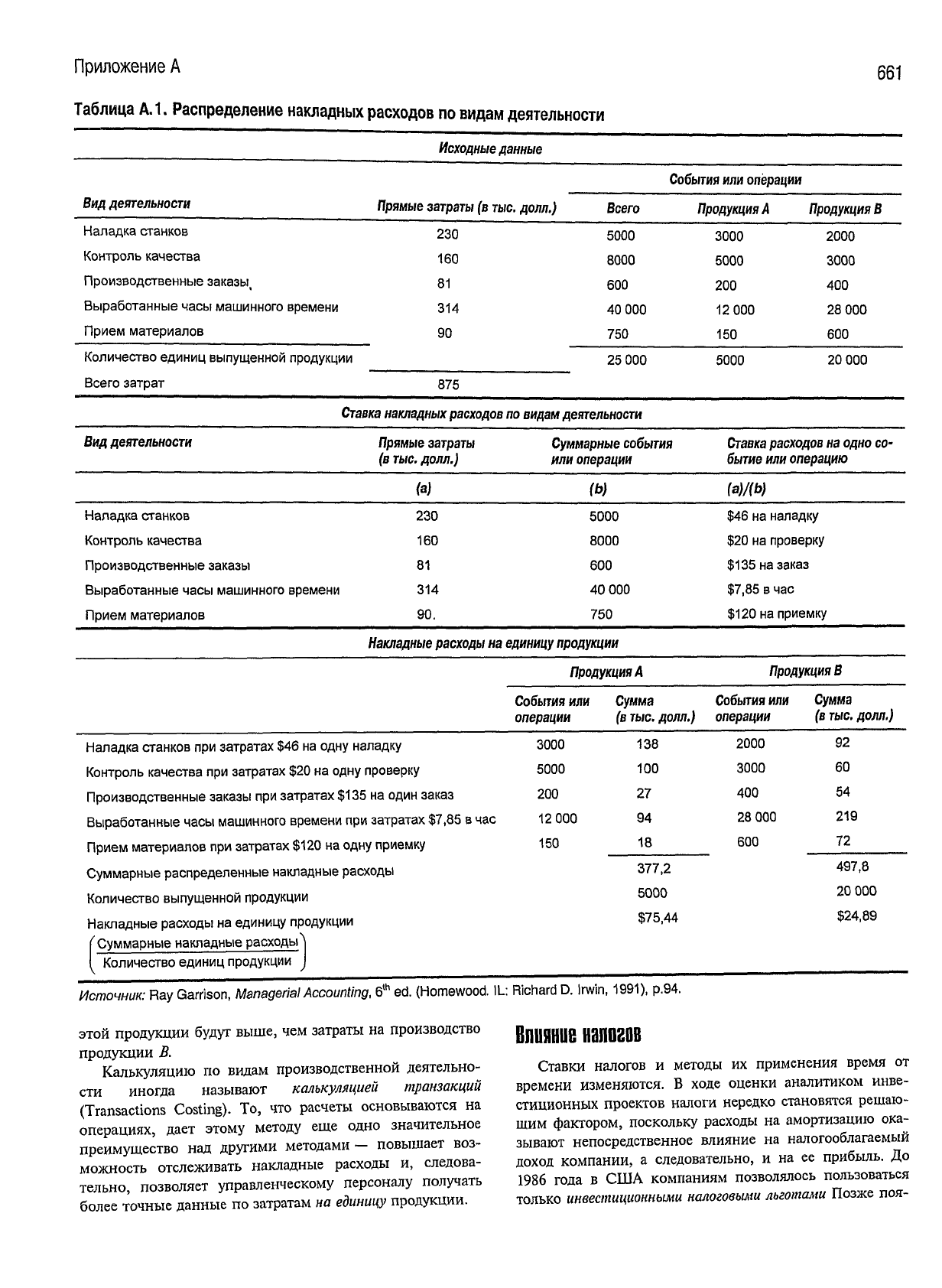
Таблица

А.1.

Распределение

накладных

расходов

по

видам

деятельности

661

Исходные

данные

События

или

операции

Вид

деятельности

Наладка

станков

Контроль качества

Производственные заказы.

Выработанные

часы

машинного времени

Прием материалов

Количество единиц выпущенной продукции

Прямые

затраты (в тыс. допл.)

230

160

314

Всего

5000

8000

600

40 000

750

25 000

Продукция

3000

5000

200

000

150

5000

Продукция

2000

3000

400

28 000

600

20 000

Всего

затрат

875

Ставка

накладных

расходов по видам

деятельности

Вид

деятельности

Прямые

затраты

(в тыс. долл.)

Суммарные

события

или операции

Ставка

расходов на одно со-

бытие

или операцию

(а)

(Ь)

Наладка

станков

Контроль качества

Производственные заказы

Выработанные

часы

машинного времени

Прием материалов

230

160

314

90,

5000

8000

600

40 000

750

$46

на

наладку

$20

на

проверку

$135 на заказ

$7,85 в

час

$120

на

приемку

Накладные

расходы на

единицу продукции

Продукция А

Продукция

События

или

операции

Сумма

(в тыс. долл.)

События

или

операции

Сумма

(в тыс. долл.)

Наладка

станков при затратах $46

на

одну наладку 3000

Контроль качества при затратах $20

на

одну проверку 5000

Производственные заказы при затратах

$135

на

один заказ

200

Выработанные

часы

машинного времени при затратах $7,85 в час 12 000

Прием материалов при затратах $120 на одну приемку

150

Суммарные распределенные накладные расходы

Количество выпущенной продукции

Накладные

расходы

на

единицу продукции

Суммарные накладные расходы^

Количество единиц продукции

138

100

377,2

5000

$75,44

2000

3000

400

28 000

600

219

497,8

20 000

$24,89

Источник:

Ray

Garrison,

Managerial

Accounting,

ed.

(Homewood.

IL:

Richard D. Irwin, 1991),

p.94.

этой

продукции

будут

выше, чем затраты на производство

продукции В.

Калькуляцию по видам производственной деятельно-

сти иногда называют калькуляцией

транзакций

(Transactions Costing). To, что расчеты основываются на

операциях,

дает

этому методу еще одно значительное

преимущество над другими методами — повышает воз-

можность отслеживать накладные расходы и, следова-

тельно, позволяет управленческому персоналу получать

более точные данные по затратам на

единицу

продукции.

Влияние

налогов

Ставки

налогов и методы их применения время от

времени изменяются. В

ходе

оценки аналитиком инве-

стиционных

проектов налоги нередко становятся решаю-

щим

фактором, поскольку расходы на амортизацию ока-

зывают непосредственное влияние на налогооблагаемый

доход

компании, а следовательно, и на ее прибыль. До

1986 года в США компаниям позволялось пользоваться

только

инвестиционными

налоговыми

льготами

Позже поя-

662

Приложения

Традиционная калькуляция

затрат

Калькуляция по видам деятельности

Суммарные

накладные

расходы

Суммарные

накладные

расходы

Распределение на основе

затрат

труда,

выраженных

часах

Затраты на

конечную продукцию

Объединение видов деятельности

Совокупные затраты

Распределение

по источникам затрат

Затраты на

конечную продукцию

Рис.

А.2. Сравнение

традиционного

метода

калькуляции

затрат

калькуляцией

по

видам

производственной

деятельности

вившаяся возможность списывать

большую

долю

аморти-

зации

ранние

годы

срока

службы

активов обеспечивает

фирмам дополнительный источник

средств

для

инвести-

ций.

Учитывая,

что

налоговое законодательство непре-

рывно изменяется, очень важно предельно внимательно

следить

за

законами

уметь

предвидеть любые измене-

ния

них, которые

могут

повлиять

на

инвестиционные

бухгалтерские

процедуры.

Выбор

инвестиционного проекта

последнее время процедура принятия инвестицион-

ных решений стала очень рациональной,

о чем

свидетель-

ствует

огромное разнообразие методов

инструментов,

используемых

для

этих целей.

отличие

от

маркетинго-

вых решений

решений, связанных

ценообразованием,

решения относительно капиталовложений

зачастую

име-

ют более высокую степень достоверности, поскольку

пе-

ременные, влияющие

на них,

относительно хорошо

из-

вестны

и их

можно определить

достаточно высокой

сте-

пенью точности.

Инвестиционные

решения можно объединить

шесть

основных групп.

1. Решения

приобретении нового оборудования и/или

производственных мощностей.

2. Решения

замене

существующего

оборудования и/или

производственных мощностей.

3. Решения типа "производить или покупать".

4. Решения типа "арендовать или покупать".

5. Решения

временной приостановке деятельности

или

закрытии предприятия.

6. Решения

добавлении новой

или

прекращении работы

существующей

производственной линии.

Инвестиционные

решения принимаются

учетом

наи-

более

низкой

приемлемой

ставки

дохода

по

инвестициям.

Изначально такая ставка может рассматриваться

как

стоимость инвестиционного капитала, необходимого

для

покрытия

всех

затрат. Само собой разумеется, никто

не

возьмется

за

реализацию инвестиционного проекта, если

нет надежды вернуть как минимум стоимость вложенного

в него капитала.

Как

правило, инвестиционные проекты оцениваются

на

основе

дохода,

который

они

приносят

сверх

стоимости

инвестируемого

в них

капитала.

этом

случае

компании

с ограниченными инвестиционными фондами

могут

вы-

брать инвестиционные альтернативы, обещающие наибо-

лее высокую

чистую

прибыль.

(Чистая

прибыль

— это

до-

ход

от

инвестированного капитала после вычитания

из

суммы валового

дохода

стоимости капитала, использован-

ного

на

финансирование инвестиций.) Инвестиционный

проект,

как

правило,

не

принимают, если денежный

до-

ход

от

него

не

превышает

предельных

издержек

по

инве-

стиционному капиталу.

(Предельные

издержки

представ-

ляют собой приростные издержки, связанные

каждым

случаем

приобретения

средств

из

внешних источников.)

Вычисление стоимости капитала

СТОИМОСТЬ

капитала

(Cost

Capital) вычисляется

на

основе взвешенного среднего значения издержек

по дол-

говым обязательствам

акционерному капиталу. Это зна-

чение может варьироваться

зависимости

от

выбранной

компанией

стратегии финансирования

. Наиболее

рас-

пространенными источниками финансирования являются

краткосрочная

долгосрочная задолженности

акции.

Примером краткосрочной задолженности может

служить

банковский

заем; продажа облигаций обычно считается

долгосрочной задолженностью,

наиболее широко

при-

меняемой формой акционерного финансирования являет-

ся

выпуск

продажа акций.

вашему вниманию

представлены примеры каждой

из

этих форм финансиро-

вания,

затем показано,

как их

объединить

для

опреде-

ления

средней взвешенной стоимости капитала.

Ставка

краткосрочной

задолженности

(Short-Term Debt)

зависит

от

процентной ставки

по

займу

и от

того,

дис-

Исследования последних

лет

показали,

что

средняя учетная

ставка

по

постоянному долларовому денежному потоку состав-

ляет 12,2%. Это выше,

чем

ставка, получаемая

результате стан-

дартного анализа стоимости капитала. См. статью James

Poterba

and Lawrence

Summers,

CEO

Survey

U.S.

Companies' Time Hori-

zons

and

Hurdle

Rates",

Sloan

Management

Review,

Fall 1995,

43-53.

Приложение А

663

контируется данный заем или нет:

Сумма выплачиваемого

Ставка краткосрочной процента

задолженности Полученные

доходы

Как

мы помним,

доходы

по процентам являются на-

логооблагаемыми потоками компании. Если банк дискон-

тирует

заем, процентная ставка вычитается из номиналь-

ной

стоимости займа, в

результате

чего вычисляется сум-

ма полученного

дохода.

Если банк

требует

наличия

компенсационного остатка на депозитном счете (т.е. в ка-

честве гарантии банк удерживает определенный процент

номинальной

стоимости займа),

доход

также сокращается.

В любом

случае

фактическая или реальная процентная

ставка по займу

будет

выше номинальной процентной

ставки из-за того, что

доход,

полученный по займу, всегда

меньше суммы (номинальной стоимости) этого займа.

Пример

краткосрочной

задолженности

Предположим, некая компания взяла в банке заем на

сумму

150 тысяч долларов сроком на один год под 13%

годовых. Данный заем дисконтируется, и банк

требует

наличия

компенсационного остатка в размере 10%. Фак-

тическая процентная ставка по данному займу вычисляет-

ся

следующим образом:

13%х$150

000

$115 500 "

89%

Доход, полученный компанией, составляет:

Номинальная

стоимость займа $150 000

За

вычетом процентов (19 500)

Компенсационный

остаток

(15 000)

(10%

$150 000)

Доход

$115

500

Обратите внимание, что фактическая процентная

ставка значительно превышает номинальную.

Долгосрочная

задолженность

(Long-Term Debt), как

правило, является результатом продажи корпорационных

облигаций. Реальную стоимость облигаций определяют

расчетом

двух

типов

доходов

— простого (номинального)

дохода

дохода,

получаемого до срока погашения

(фактическая процентная ставка). Первый показатель

проще прогнозировать, но второй более точен. Номи-

нальная процентная ставка равняется номинальному вы-

плаченному проценту (стоимость на момент погашения)

по

облигации и всегда заявляется на годовой основе. Об-

лигации, как правило, выпускаются номиналом 1000 дол-

ларов и продаются по стоимости выше номинальной

(сверх паритета) либо ниже номинальной (Original

Issue

Discount — OID), т.е. со скидкой с номинальной цены

ценной

бумаги на момент ее выпуска. Облигации прода-

ются со скидкой, если процентная ставка по ним ниже

текущей рыночной ставки. В этом

случае

доход

будет

вы-

ше номинальной процентной ставки. Если облигации вы-

пускаются по стоимости выше номинала,

доход

будет

ни-

же номинальной процентной ставки.

Курс выпуска облигаций представляет собой номи-

нальную стоимость, умноженную на

сумму

надбавки (или

скидки):

Простой

доход

= Номинальная процентная ставка

Курс выпуска облигации

Г Доход, получаемый до срока

[ погашения задолженности

(

Номинальная

^ Скидка (надбавка)

[ сумма процентов

Количество лет

Курс облигаций

Стоимость на

момент погашения

Пример

долгосрочной

задолженности

Предположим, некая компания выпустила 12%-ные

облигации на

сумму

400 тысяч долларов, со сроком пога-

шения

10 лет по номинальной стоимости 97%. Вычисле-

ние

дохода

выполняется следующим образом:

Номинальный

ежегодный

12%

$400

000

$48 000

платеж

Поступления

от

продажи

97%

$400

000

$388

000

облигации

Скидка

против

номинала

$400

000

$12 000

Простой

доход

Доход

до

срока

погашения

12%х$400

000

97%х$400

000

$48 000+

$12 000

$388

000+$400 000

= 12,5%

Обратите внимание, поскольку облигации продаются

со скидкой,

доход

превышает номинальную процентную

ставку 12%. Процент по облигационным займам является

налогооблагаемым показателем.

Ставка

резервных

акций

(Cost Of Equity Securities) высту-

пает в форме дивидендов, налог по которым не взимается:

Ставка резервных акций =

(

Дивиденд в ^

[ расчете на акцию

['Темпы роста"|,

(

Стоимость "| I дивидендов J

[одной

акцииJ

где стоимость одной акции равна разнице рыночного курса

акции

и стоимости выпуска новых акций (т.е. затрат, связан-

ных с выпуском ценных

бумаг,

например, на оплату комис-

сионных брокеру, затраты на печать и т.д.).

Следует

отме-

тить, что такая оценка не учитывает ожидание инвестором

повышения

рыночного курса. Это ожидание основано на

прогнозируемых темпах роста

дохода

в расчете на одну ак-

цию и на соответствующей степени риска, принимаемого

при

приобретении данных акций. Для того чтобы

учесть

оба

этих фактора, используется модель ценообразования основ-

ного капитала (Capital

Asset

Pricing Model — САРМ)

Описание модели САРМ можно найти во многих учебниках по

финансам.

См., например, Zvi Bodie,

Alex

Kane

and Alan

Marcus,

In-

vestment,

ed.

(Burr

Ridge,

IL:

Richard

Invin,

1996),

236-265.

664

Приложения

Пример

определения

ставки

резервных

акций

Компания

платит дивиденды в размере 10 долларов,

чистая стоимость на одну акцию — 70 долларов, темп

роста дивидендов 5%. Тогда

Стоимость акций

%£•

0,05 = 19,3%.

$70

Для того чтобы вычислить

взвешенную

среднюю

стои-

мость

капитала

(Weighted

Average

Cost Of Capital), берется

процент

совокупного капитала по каждой имеющейся

финансовой

альтернативе. Затем вычисляется стоимость

каждой такой альтернативы после уплаты налогов. И на-

конец,

определяется весовой коэффициент каждой стои-

мости пропорционально степени их использования.

Пример

вычисления

взвешенной

средней

стоимости

ка-

питала

Рассмотрим пример компании, в финансовой отчетно-

сти которой приведены следующие показатели:

Краткосрочный банковский

заем (13%)

Облигации

оплате

(16%)

Обыкновенные

акции (10%)

1 миллион

долларов

миллиона долларов

5 миллионов долларов

В нашем примере мы

будем

исходить из предположе-

ния,

что каждый приведенный выше процентный показа-

тель отображает стоимость источника капитала. Кроме

этих данных нам

следует

учесть

ставку налога компании,

поскольку проценты, выплачиваемые по облигациям и

краткосрочному займу,

будут

налогооблагаемыми. Пред-

положим, что корпоративная налоговая ставка компании

составляет 40%.

Краткосроч-

ный банков-

ский

заем

Облигации

оплате

Обыкновен-

ные акции

Итого

Про-

цент

10%

40%

50%

100%

Стоимость

после

уплаты

налогов

13%х60%

= 7,8%

16%х60%

= 9,6%

10%

Взвешенная

сред-

няя

стоимость

0,78%

3,84%

9,62%

Следует

помнить, что все вычисления, приведенные в

данном

разделе, проводились на основе множества допу-

щений.

При использовании описанных выше концепций

конкретной компании эти допущения

могут

очень

сильно

меняться, однако основные понятия останутся не-

изменными.

Не забывайте, что главная цель заключается

в определении стоимости капитала, используемого ком-

панией,

после выплаты налогов. В нашем примере мы

использовали показатель совокупного капитала фирмы,

но

во многих

случаях

вычисления выполняются только

относительно капитала, занятого в конкретном проекте.

Влияние процентной ставки

Существует

два основных метода расчета эффекта на-

копления

процентов. Один из них заключается в вычис-

лении

общей суммы, получаемой в течение определен-

ного временного периода на конкретный момент в

буду-

щем,

т.е. в определении

будущей

стоимости.

Второй

наоборот, предусматривает приведение

будущих

денеж-

ных потоков и соответствующих процентов к настоящему

времени,

т.е. определяется

нынешняя

стоимость.

Будущая стоимость Единичной суммы

Сегодня нередко приходится слышать высказывание

Альберта

Эйнштейна, который назвал сложные проценты

восьмым

чудом

света. Возможно, что, ознакомившись с

содержанием данного раздела, в котором говорится о

внушительном эффекте роста процента в течение дли-

тельного периода времени, вы предложите новый

госу-

дарственный закон: при рождении ребенка родители бу-

дут обязаны открыть пенсионный счет в размере 1000

долларов, которым он сможет воспользоваться, достигнув

65-летнего возраста. Это могло бы снизить давление на

социальную

службу

другие

государственные и феде-

ральные планы пенсионного обеспечения. Конечно, ин-

фляция

значительно понизит стоимость вклада, но все

равно большая часть останется. При 14%-ном

доходе

на

инвестированный

капитал (а в наши дни многие

финан-

совые учреждения предлагают долгосрочные проценты

под более чем 14%) наши 1000 долларов

дадут

за 65 лет

сумму

500 тысяч долларов (это после вычитания

инфля-

ционных

4,5 миллионов долларов). Таким образом,

даже

учетом

инфляции

будет

500-кратное увеличение.

Подобные вычисления без

труда

можно выполнить с

помощью электронных таблиц и калькулятора. Во врезке

"Использование

электронных таблиц Excel" описаны не-

которые наиболее употребительные финансовые функции

Excel. Однако многие и сегодня предпочитают пользо-

ваться таблицами сложных процентов. Так, например,

воспользовавшись табл. G.1, приведенной в Приложе-

нии

G, мы можем определить, что стоимость 1 доллара

при

10%-ной ставке через три

года

составит 1,331 долла-

ров.

Умножив эту цифру на 10 долларов, мы получим

сумму

13,31 долларов.

Аннуитет

Аннуитетом

называют ежегодное поступление одина-

ковых сумм на протяжении определенного количества

лет. Обычно выплата по аннуитету поступает на конец

периода (года) и процент за истекший период не начис-

ляется.

Таким образом, аннуитет в размере 10 долларов на

три

года

принесет 10 долларов на конец первого

года

(при

этом данная сумма приносит определенное процентное

поступление за оставшиеся два года), 10 долларов на ко-

нец

второго

года

с процентами за оставшийся один год и

10 долларов на конец третьего

года

(времени на начисле-

ние

процента не остается). Если поступления по аннуите-

ту в 10 долларов были помещены на сберегательный

Приложение

665

Применение

электронных таблиц Excel

Описанные

выше расчеты должны освоить все студенты, работая на компьютере с использованием элек-

тронных таблиц. Однако, несмотря на то, что соответствующее программное обеспечение значительно уп-

рощает процедуру вычислений, очень важно понимать, что же на самом

деле

делает компьютер. Кроме того,

следует

уметь проверять расчеты без использования компьютерной техники, чтобы убедиться, что в элек-

тронных таблицах использовались правильные формулы. Рассказывают немало страшных историй об ужас-

ных последствиях неправильных решений из-за ошибок при использовании электронных таблиц.

В этой врезке вашему вниманию представлено краткое описание наиболее употребительных

финансо-

вых функций. Они взяты из справочного материала по Microsoft Excel.

PV(rate,

nper,

pint). Данная функция определяет (возвращает) нынешнюю стоимость инвестиций. Ны-

нешняя

стоимость - это общая сумма ряда

будущих

платежей, приведенная к настоящему времени. Так,

например,

когда мы одалживаем деньги, сумма займа

будет

для кредитора нынешней стоимостью.

Rate

(ставка) — это процентная ставка за определенный период. Например, если вы получили заем на приоб-

ретение автомобиля под 10% годовых и проводите платежи ежемесячно, процентная ставка в месяц

будет

10%/12

= 0,83%. Таким образом, в качестве ставки в формулу

следует

ввести

10%/12,

0,83% или

0,0083.

Nper

— это общее количество периодов платежей по аннуитету. Например, если вы получили четырехго-

дичный

заем на приобретение машины и проводите платежи ежемесячно, то ваш заем распределен на

4 х 12 (или 48) периодов. Следовательно, в качестве показателя

nper

вводим в расчет число 48.

Pint—

это

сумма платежа в каждый период, которая должна быть неизменной и одинаковой на протяжении всего

срока

аннуитета. Как правило, она состоит из основной суммы и суммы процентных платежей и не

включает никаких

других

сборов и налоговых платежей. Так, например, ежемесячный платеж по четы-

рехлетнему займу в размере 10 тысяч долларов, взятому под 12%, составляет

263,33

доллара. Это значение

вводится в расчет как показатель pmt.

(rate,

nper,

pmt). Данная функция служит для расчета

будущей

стоимости инвестиций, предусмат-

ривающих периодические одинаковые платежи и постоянную процентную ставку.

Rate

— это показатель

процентной

ставки за один период,

nper

— общее количество периодов аннуитета, a pmt — платеж, про-

водимый в каждый период, который остается неизменным на протяжении всего срока аннуитета. Этот

показатель обычно включает основную

сумму

выплат процентного платежа и не содержит ка-

ких-либо

других

сборов или налоговых платежей.

NPV

(rate,

valuel,

value2,

...). Данная функция определяет чистую нынешнюю стоимость инвестиций,

основанную на ряде периодических денежных потоков и конкретной учетной ставке. Чистая нынешняя

стоимость инвестиций — это стоимость ряда

будущих

платежей (отрицательные значения) и прибылей

(положительные значения) на сегодня.

Rate

— это учетная ставка за один период. Значения

valuel,value2,

...

должны быть равномерно распределены во времени и приходятся на конец каждого периода.

JRR

(values). Эта функция определяет внутреннюю ставку доходности последовательности денежных

потоков,

представленных определенным количеством значений. Предполагается, что в этом

случае

де-

нежные потоки не одинаковы, как при аннуитете. Внутренняя ставка доходности - это процентная став-

ка

по инвестициям, определяемая по платежам (отрицательные значения) и прибылям (положительные

значения),

учитываемым с определенной периодичностью.

Values

- это ряд данных или ссылок на ячей-

ки,

содержащий числа, для которых вы хотели бы вычислить внутреннюю ставку доходности. Для таких

вычислений

values

должны включать как минимум одно положительное и одно отрицательное значения.

При

вычислении внутренней ставки доходности порядок ввода значений должен соответствовать порядку

поступления и выбытия денежных потоков, поэтому

будьте

внимательны и вводите значения платежей и

прибылей в нужной последовательности.

Источник.

Microsoft Excel,

Version

7, справочные материалы по использованию финансовых

функций.

666

банковский

счет под 5% годовых сроком на три

года,

об-

щая

будущая

стоимость данной суммы

будет

следующей:

Год

Поступление

на

конец

года

(в

долл.)

10,00

Коэффициент

сложных

про-

центов

(1+0"

(1+0.05)

(1+0,50)°

Стоимость

на

конец

третьего

года (в долл.)

11,02

10,50

10,00

$31,52

Общая формула для вычисления

будущей

стоимости

аннуитета имеет следующий вид:

Rf(l+ i)n-l+(l+

0n-2+...(J+

i)l+lj,

где S

—

будущая

стоимость аннуитета;

— периодические поступления в долларах;

п — продолжительность аннуитета в

годах.

Применив

эту формулу к описанному выше примеру,

получаем:

= R[(l+i)2+(l+i) + 1] =

$10[(1+0,05)2+(1+0,05)+1]

$31,52.

В табл. G.2 в Приложении G находим, что

коэффици-

ент

будущей

стоимости суммы в

доллар при 5%-ной став-

ке

и трехгодичном аннуитете равен

3,152.

Умножив этот

показатель на 10 долларов, получаем значение 31,52 долл.

Способом,

аналогичным описанному в предыдущем

примере,

рассмотрим преимущества ежегодного инвести-

рования

2000

долларов в пенсионный фонд, начиная с 21-

летнего возраста. Предположим, вы можете приобретать

облигации высшего класса по рейтингу агентства

Standard&Poor,

приносящие

9%-ную

прибыль. Воспользо-

вавшись табл. G.2 в Приложении G, находим, что по ис-

течении 30 лет (т.е. когда вы достигнете 51

года)

сумма

ваших накоплений составит 136,3 х

2000

долларов, т.е.

272 600 долларов. Спустя еще 14 лет (когда вам исполнит-

ся

65 лет) сумма накоплений увеличится до 963 044 дол-

ларов. (Эта сумма определена на карманном калькулято-

ре,

поскольку в табл. G.2 приведены значения только для

тридцатилетнего периода. Кроме того, эта сумма

будет

получена вами только при условии, что, начиная с 21-

летнего возраста, на конец каждого

года

вы

будете

откла-

дывать на счет

2000

долларов.) Таким образом, без особых

усилий вы к пенсионному возрасту становитесь миллио-

нером!

Но кто задумывается о пенсии в 21 год?!

Нынешняя стоимость Оудущего единичного платежа

Концепция

будущей

СТОИМОСТИ

используется для оп-

ределения размеров

будущих

платежей по истечении оп-

ределенного периода времени. Процедура определения

нынешней

стоимости (Present

Value

— PV) является об-

ратной.

Ее используют для определения стоимости на

данный

момент потока поступлений, которые ожидаются

будущем.

Большинство методов принятия инвестици-

онных

решений основано не на

будущей

стоимости, а

Приложения

именно

на концепции нынешней стоимости. Посколь

решения,

влияющие на

будущее,

принимаются инвесто-

рами сегодня, целесообразнее преобразовать

будущие

по-

ступления в показатели их нынешней стоимости на мо

мент принятия решения. В этом случае, на основе ны-

нешних

долларовых показателей, можно более точно

оценить

инвестиционные альтернативы.

Эта идея

будет

понятнее, если объяснить ее на кон-

кретном примере. Представьте, что богатый дядюшка

предложил вам в подарок 100 долларов сегодня или 250

долларов через десять лет. Какой вариант вы выбрали бы?

Вам необходимо определить,

будут

ли 250 долларов спустя

десятилетие стоить больше, чем сегодня стоят 100 долла-

ров.

Предположим, что ваше решение основано на кон-

кретном уровне инфляции в экономике вашей страны и

вы считаете, что средний уровень инфляции

будет

10% в

год. Дефлировав

сумму

в 250 долларов, вы сможете срав-

нить

ее покупательную способность с покупательной спо-

собностью суммы в 100 долларов на сегодня. В соответст-

вии

с принятой процедурой эта операция выполняется

решением уравнения приведения

будущей

стоимости, ис-

ходя из формулы:

К=

Р(\ + /)«,

где

—

будущая

стоимость (250 долларов) по истечении

10-летнего периода при 10%-ной инфляции.

Разделив обе части уравнения на (1 +

/)",

получаем:

250

0,10)"

$96,39.

Таким

образом, мы видим, что при 10%-ной

инфля-

ции

сумма 250 долларов через 10 лет

будет

соответство-

вать сумме

96,39

долларов на сегодня. Следовательно, це-

лесообразнее принять от дяди 100 долларов сегодня.

При

решении задач, связанных с определением теку-

щей

стоимости, также часто пользуются специальными

таблицами. Так, воспользовавшись табл. G.3 в Приложе-

нии

G, мы легко можем определить, что коэффициент

нынешней

стоимости 1 доллара, полученного по истече-

нии

10-летнего периода,

будет

0,386.

Умножив этот ко-

эффициент

на 250 долларов, получаем примерно тот же

результат

—

96,50

долларов.

Нынешняя стоимость аннуитета

Нынешняя

СТОИМОСТЬ

аннуитета — это стоимость

ежегодных одинаковых поступлений в течение опреде-

ленного периода, выраженная в сегодняшних показателях.

Чтобы определить стоимость трехгодичного аннуитета в

100 долларов при 10%-ной ставке, находим в табл. G3

Приложения

G коэффициенты приведения нынешней

стоимости для 10%-ной ставки в

каждый

год из

трехлет-

него периода, в течение которого поступают платежи по

аннуитету, и умножаем каждое поступление на соответст-

вующие коэффициенты. После этого суммируем полу-

ченные значения. Помните, что аннуитетные платежи

обычно поступают на конец каждого периода.

Приложение

667

Год Сумма,

полу-

ценная

на ко-

нец

года

(в долл.)

Коэффициент

приведения

стоимости

при 10%

Нынешняя

стоимость

(в

долл.)

100

300

0,909

0,826

0,751

90,90

82,60

75,10

248,60

Общая

сумма

поступлений

** -

Суммарная

нынешняя

стоимость

Общая формула для расчета нынешней стоимости ан-

нуитета имеет следующий вид:

+ ... + •

[ + /)"

где А„ — нынешняя стоимость аннуитета сроком на п лет;

R — периодические поступления по аннуитету;

п — продолжительность аннуитета в

годах.

Применив

данную формулу к описанному выше при-

меру, получаем:

=$100

1 1

$248,70.

(1 +

0,10) Ц

0,10)

"•

(1 +

0Д0)

В табл. G.4 в Приложении G приведены

коэффициен-

ты нынешней стоимости аннуитета с разными сроками

платежа. Как мы видим, коэффициент нынешней стои-

мости для трехгодичного аннуитета на 1 доллар при 10%-

ной

ставке равен

2,487

(табл. G.4, Приложение G). Учи-

тывая, что в условиях нашей задачи указана сумма не 1, а

100 долларов, умножаем этот коэффициент на 100 долла-

ров и получаем значение

248,70

долларов.

Если же поток

будущих

поступлений неравномерен,

необходимо отдельно вычислять нынешнюю стоимость

каждого ежегодного поступления. После этого значения

нынешних стоимостей поступлений за все годы сумми-

руются, в

результате

получаем суммарную нынешнюю

стоимость. Эта процедура иногда бывает трудоемкой и

длительной, но обойтись без нее невозможно.

Дисконтированный

денежный

поток

Термин дисконтированный денежный поток (Discounted

Cash Flow) применяется для определения стоимости в на-

стоящий момент общего потока платежей, которые

будут

результатом использования активов в

будущем.

Дискон-

тирование денежного потока — это не что иное, как при-

ведение к нынешней стоимости всех потоков: единичных

платежей, аннуитетов и т.д.

Методы

сравнения инвестиционных проектов

Чистая

текущая

стоимость

В бизнесе для сравнения инвестиционных проектов

обычно используется показатель чистой нынешней стои-

мости. Применение его, как правило, основывается на

определении превышения нынешней стоимости прогно-

зируемого потока прибыли над стоимостью инвестиций.

Предположим, фирма рассматривает инвестиционные

альтернативы. Первая оценивается в 30 тысяч долларов, а

вторая — в 50 тысяч долларов. Ожидаемые ежегодные по-

токи прибыли указаны в приведенной ниже таблице.

Входящий

денежный

поток

(тыс.

долл.)

Год

Альтернатива

Для того чтобы выбрать наиболее выгодную из этих

двух

альтернатив, необходимо определить, какая из них

имеет более высокую чистую текущую стоимость. Пред-

положим, что ставка стоимости капитала составляет 8%.

Альтернатива

3,993

(коэффициент

PV)

х $10 000 = $39 930

Минус

стоимость

инвестиций

$30 000

Чистая

текущая

стоимость

$9930

Альтернатива

3,993

(коэффициент

PV)

х $15 000 = $59 895

Минус

стоимость

инвестиций

$50

000

Чистая

текущая

стоимость

$9895

Таким

образом, как мы видим, альтернатива А более

выгодна. Ее чистая текущая стоимость превышает данный

показатель альтернативы В на 35 долларов ($9 930 -

$9 895 = $35).

Период окупаемости

Период окупаемости (Payback Method) служит для

сравнения

инвестиций по времени, необходимому для

того, чтобы инвестиции принесли прибыль, равную их

стоимости. Идея в данном

случае

заключается в том, что,

чем быстрее вы сможете возвратить инвестированный ка-

питал, тем быстрее его можно

будет

вновь вложить в но-

вый прибыльный проект. Таким образом, фирма получит

большую прибыль от имеющихся в ее распоряжении ин-

вестиционных средств.

Сравним два инвестиционных проекта, для реализа-

ции

которых необходимо 1000 долларов. Первый проект

обещает приносить прибыль 200 долларов ежегодно на

протяжении последующих шести лет, а второй — по 300

долларов первые три года и по 100 долларов в год в по-

следних три года.

Если выбрана первая альтернатива, исходная инвестиро-

ванная

сумма 1000 долларов

будет

возвращена по истечении

пятого года; прибыль же, полученная при выборе второй

альтернативы, достигнет суммы 1000 долларов уже на конец

четвертого года. Следовательно, при второй альтернативе вы

сможете реинвестировать средства в размере 1000 долларов в

новый

приносящий прибыль проект на год раньше, чем при

выборе первого варианта вложения средств.

668

Приложения

Несмотря

на

то,

что в

последнее время оценка инве-

стиций

на

основе периода окупаемости

виде самостоя-

тельного аргумента для принятия инвестиционного реше-

ния

применяется все реже,

ее

по-прежнему часто исполь-

зуют

комбинации

другими методами для определения

временных затрат вложенных средств. Основные пробле-

мы данного метода заключаются

том, что не учитывает-

ся

прибыль, получаемая вне пределов периода окупаемо-

сти,

также

то, что при его

применении игнорируется

обесценивание денег.

Следует

всегда помнить,

что

реше-

ния,

принимаемые

использованием любого метода,

не

учитывающего изменения стоимости денег

во

времени,

необходимо подкреплять какими-либо другими способа-

ми

процедурами.

Внутренняя

ставка доходности

Внутреннюю ставку

ДОХОДНОСТИ

(Internal Rate

Return)

можно определить

как

процентную ставку, уравниваю-

щую нынешнюю стоимость потока прибыли

со

стоимо-

стью инвестиций. Процедуры или формулы

для

прямого

вычисления внутренней ставки доходности не

существует.

Этот показатель получают путем интерполяции либо

ре-

зультате

итерационных вычислений.

Предположим, мы хотим вычислить внутреннюю став-

ку доходности инвестиций стоимостью 12 тысяч долларов,

при

которых ожидается ежегодный входящий денежный

поток

размере

тысячи долларов

на

протяжении четы-

рех лет. Коэффициент нынешней стоимости вычисляется

следующим образом:

Далее нам необходимо найти процентную ставку,

при

которой

течение четырехлетнего периода

будет

получен

данный

коэффициент. Поскольку коэффициент

3,000

на-

ходится

диапазоне

2,914—3,037

(см.

четвертую

строку

табл. G.4 Приложения

G),

эта

процентная ставка должна

быть

диапазоне

между

12 и

14%. Линейная интерполя-

ция

этих значений

дает

результат:

В итоге

мы

получаем достаточно точный показатель

фактической

внутренней ставки доходности.

Дисконтировав входящий денежный поток

на

12,6%,

мы получаем нынешнюю стоимость, наиболее близкую

стоимости инвестированных средств. Следовательно,

внутренняя ставка доходности

по

данной инвестиции

равна

12,6%.

После этого можно сравнить стоимость

ка-

питала

этим показателем

определить чистую ставку

доходности

по

этой инвестиции. Например,

при

ставке

стоимости капитала

чистая ставка доходности

от

ин-

вестиций была бы 4,6%.

В основе методов оценки инвестиций

по

чистой теку-

щей

стоимости

внутренней ставке доходности лежат,

сущности, одинаковые процедуры. Они отличаются

тем,

что при использовании метода чистой нынешней стоимо-

сти инвестиционные альтернативы сравниваются

на ос-

нове долларовой суммы превышения стоимости инвести-

рованных средств,

в то

время как метод внутренней став-

ки

доходности позволяет сравнивать ставки

дохода

альтернативных инвестиций.

Следует

отметить,

что при

применении

второго метода часто приходится сталкивать-

ся

вычислительными проблемами, поскольку этот метод

основан

на многоитерационных операциях.

Сравнение проектов с разными

продолжительно

cm я

ми

ЕСЛИ

инвестиционные проекты имеют одинаковую

продолжительность,

их

сравнение

использованием опи-

санных выше методов

дает

довольно точную картину со-

отношения

их

стоимостей. Если же сроки разные, возни-

кает

ряд

вопросов.

Как

сравнивать такие инвестиции?

Следует

ли

рассматривать замещаемое оборудование

так

же, как

первоначальное? Как учитывать разную произ-

водительность оборудования

инвестиционных альтерна-

тивах?

Каким образом

следует

оценивать стоимость вво-

димой единицы оборудования?

В таких случаях никакие предварительные оценки ин-

вестиций,

по

которым принимаются решения,

не

могут

дать высокой степени точности. Поэтому при сравнении

разных инвестиционных альтернатив необходимо учиты-

вать все принимаемые допущения.

Примеры

задач:

инвестиционные

решения

Пример

А.1.

Решение

расширении

предприятия

Компания

William

Wilson Ceramic

Products,

Inc. арендует

предприятие

по

производству

огнеупорного

кирпича.

Поскольку

последнее

время наблюдается устойчивый

рост

спроса

на дан-

ную

продукцию,

определили,

что фирма

может

увеличить объемы

продаж,

инвестировав средства

новое

оборудование

и тем са-

мым

увеличив объем выпуска

кирпичей.

Продажная цена

состав-

ляет 10 долларов за единицу

продукции,

планируется,

что по-

сле

увеличения объемов выпуска и

продаж

она не

изменится.

На

основе

заводской

проектной

оценки

эксплуатационных

расходов

оценки

издержек

производства

бухгалтерия предоставила

руко-

водству

смету.

По

данной

смете

планируется

увеличение

ежегод-

ного

объема

производства

на

100

тысяч

кирпичей.

Стоимость

нового

оборудования

ожи- 500 тыс.

долл.

даемым

сроком

службы пять лет

Затраты

на

установку

нового

оборудования

тыс.

долл.

Ожидаемая

ликвидационная

стоимость

Доля

новых

операций

в затратах на опла- 40

тыс.

долл.

ту

аренды

(в год)

Повышение

затрат на оплату

коммуналь-

тыс.

долл.

ных

услуг (в год)

Повышение

затрат на оплату труда (в

год) 160 тыс.

долл.

Дополнительные

затраты на сырье (в год) 400

тыс.

долл.

Для

начисления амортизации планируется использовать

метод

суммы целого числа лет

службы,

налоговая ставка 40%.

Политика

компании предусматривает вложение инвестиций

только

проекты

прогнозируемой

ставкой дохода

не

менее

20%.

Следует ли фирме

реализовать

данный проект?

Приложение А

Решение

Вначале

вычисляем сумму инвестиций:

Затраты на приобретение нового 500 тыс

долл

оборудования

Затраты на установку нового 20

тыс.

долл

оборудования

Общая

стоимость проекта 520

тыс.

долл.

Затем определяем ежегодные денежные потоки на протяже-

нии

всего проекта.

Затраты на оплату аренды являются невозмещаемыми из-

держками.

Это означает, что компания будет

нести

их независимо

от

того,

будет она реализовывать данный проект или нет. Следо-

вательно, эти затраты не зависят от принятого решения, и их

можно

опустить.

Учитывать

следует такие ежегодные производ-

ственные

издержки,

как затраты на оплату коммунальных услуг,

труда и

сырья,

что в

сумме

дает

600

тысяч

долларов в год.

Ежегодный валовой доход от продаж составит $10 х 100 000

единиц

продукции, т.е.

миллион долларов. Таким образом,

ежегодная прибыль перед амортизационными отчислениями и

налоговыми выплатами будет равна разнице валового дохода

миллион долларов) и суммы

учитываемых

издержек (600 ты-

сяч долларов), т.е. 400

тысяч

долларов.

Далее определяем сумму амортизационных отчислений, ко-

торые будут взиматься с суммы прибыли (400

тысяч

долларов),

методом суммы целого числа лет службы (эта сумма равна

1 +2 + 3 + 4 + 5 = 15).

Год

Взимаемая доля

амортизации

от сум-

мы 500 тыс. долл.

5/15

4/15

3/15

2/15

1/15

Накопленная амортизация

х 500 000

500

000

500

000

500

000

500

000

Амортизацион-

ные

отчисления

(в долл.)

= 166

667

= 133

333

= 100

000

66 667

33 333

500 000

Теперь нужно вычислить ежегодный денежный поток при

налоговой ставке 40%. Для примера покажем, как он рассчиты-

вается для первого года:

Прибыль

до

уплаты

налогов и

амортизационных отчислений

Вычесть:

Налог

40%

(40% х 400 000)

Минус выигрыш на налогах вслед-

ствие отчислений на амортизацию

(40%

166

667)

Денежный поток первого года

400

тыс.

долл.

160

тыс.

долл.

66 667

долл.

333

долл.

306

667

долл.

После этого определяем нынешнюю стоимость денежного

потока.

Поскольку компания

Wilson

принимает в работу только

проекты,

в которых ставка дохода по инвестициям не менее

20%,

умножаем показатели потоков наличности на 20%-ный ко-

эффициент нынешней стоимости в каждый год. В данном слу-

чае, поскольку денежные потоки не являются аннуитетными,

669

для каждого года необходимо использовать свой конкретный

коэффициент.

Год

Коэффициент

ны-

нешней

стоимости

0,833

0,694

0,579

0,482

0,402

Денежный

поток

306 667

293

333

280

000

266 667

253

334

Общая

нынешняя

стоимость

денежного

потока

(дисконтированного по ставке 20%)

Нынешняя

сто-

имость

[в

долл.)

255

454

203

573

162

120

128

533

101

840

851 520

Далее следует выяснить,

является

чистая нынешняя

стои-

мость

положительным или отрицательным значением:

Суммарная нынешняя стоимость

$851

520

денежных потоков

Общая

стоимость инвестиций 520 000

Чистая нынешняя стоимость $331 520

Как

мы видим, чистая нынешняя стоимость при 20%-ном

дисконтировании

будет положительной. Компания получит при-

быль

в размере 20% от суммы инвестиций. Следовательно,

данный проект стоит реализовать.

Пример А. 2.

Решение

замене

оборудования

Компания

Bennie's

Bewery использует в своем технологиче-

ском

процессе станок для наклейки этикеток на бутылки. Этот

станок

был приобретен по цене 4 тысячи долларов и на протя-

жении 10 лет проводились амортизационные отчисления мето-

дом

равномерного начисления амортизации, в результате чего

по

истечении данного периода ликвидационная стоимость стан-

ка

достигла 0 долларов. В настоящее время можно продать

станок

за 2 тысячи долларов. Компания может приобрести но-

вый станок за 6

тысяч

долларов, срок полезной службы которо-

го

пять лет, а затраты на оплату рабочей силы при его эксплуа-

тации сокращаются на 1200 долларов в

год.

В последующие не-

сколько

лет старый станок потребует капитального ремонта,

приблизительная стоимость которого составляет 300 долларов.

При покупке нового станка амортизация будет начисляться на

протяжении пяти лет методом равномерного начисления. Лик-

видационная стоимость нового станка составит 500 долларов.

Компания инвестирует средства в проекты только при условии,

что планируемая прибыль составляет не менее 12% от стоимо-

сти

вложенного капитала. Ставка налога 40%.

Следует

ли

Bennie's

Bewery

инвестировать средства в данный проект?

Решение

Вначале

вычисляем сумму инвестиций в

долларах:

Цена нового станка 6000

За

вычетом:

Стоимости продажи старого станка 2000

Издержек

на капитальный ремонт 300 2300

Реальная

сумма инвестиций 3700

Затем вычислим сумму увеличения денежного потока при

условии инвестирования средств в новый станок:

670

Приложения

Ежегодная экономия затрат составляет

1200 долл.

Разница амортизационных отчислений

Ежегодная амортизация старого станка:

(Ликвидационная^

Стоимость-

[

стоимость j _

Ожидаемый

срок

службы

4000-0

= 400 долл.

Ежегодная амортизация нового станка:

('Ликвидационная^

Стоимость-

стоимость

Ожидаемый срок службы

6000-500

„

пп

= 1100 долл.

Разница амортизационных отчислений:

1100-400 = 700 долл.

Чистое увеличение входящего денежно-

го

потока (в год):

Экономия затрат 1200

За

вычетом: налоги в размере 40% 480

Плюс: выигрыш вследствие увеличения 280 200

амортизационных отчислений (0,4 х 700)

Увеличение

денежного потока (в год) 1000

Определяем суммарную нынешнюю

стоимость

инвестиций:

Пятилетний денежный поток в размере

1000 долл.

является

аннуитетным:

Нынешняя

стоимость капитала при

12%-ном

дисконтировании:

3,605 х 1000 = 3605 долл.

Нынешняя

стоимость нового станка при

условии его продажи по ликвидационной

стоимости

500 долл. на конец пятого года:

0,567 х 500 = 284 долл.

Суммарная нынешняя стоимость

ожидаемых потоков наличности:

3605 + 284 = 3889 долл.

Теперь определим,

является

ли чистая нынешняя стоимость

положительным или отрицательным значением:

Суммарная нынешняя стоимость потоков 3889

Стоимость инвестиций 3700

Чистая нынешняя стоимость 189

Таким образом, мы видим, что компании Bennie's Bewery

следует приобрести новый станок, поскольку

полученная

в ре-

зультате

прибыль будет несколько выше стоимости инвестиро-

ванного капитала.

Примечание. Данный пример наглядно продемонстрировал

значение

амортизации.

Нынешняя

стоимость

годового

денежно-

го

потока от операций:

(Экономия

затрат - Налоги) х (Коэффициент нынешней стоимости)

(1200

- 480) х 3,605 = 2596 долл.

Данная цифра на 1104

доллара

меньше стоимости инвести-

ций

(3700 долларов). Следовательно, реализация этого проекта

может

быть

оправдана только очень значительными выгодами в

результате начисления амортизации. Суммарная нынешняя

стоимость

этой

выгоды составляет 1009 долларов:

(Ставка налога х Разность сумм амортизации при условии ин-

вестирования и при отказе от них) х (Коэффициент нынешней

стоимости)

(0,4

х 700) х 3,605 =1009 долл. .

Пример А.З. Решение

типа

"производить

или

покупать"

Компания Triple X специализируется на производстве и про-

даже холодильников. Одни комплектующие для холодильников

она выпускает, а другие приобретает у поставщиков. Специали-

сты

конструкторско-технологического

отдела считают, что ком-

пания,

по всей вероятности, сможет сократить свои затраты,

если самостоятельно будет производить одну из деталей, кото-

рая на данный момент закупается по цене 8,25

доллара

за еди-

ницу. Ежегодно производством используется 100

тысяч

таких

комплектующих. На основании предварительных

данных

этого

отдела бухгалтерия предоставила следующую смету:

Постоянные издержки повысятся на 50

тысяч

долларов.

Затраты на оплату труда

увеличатся

на 125

тысяч

долларов.

Накладные

заводские расходы (которые на текущий момент

составляют 500

тысяч

долларов в год) могут повыситься на

12%.

Сырье

для производства новой комплектующей будет сто-

ить 600

тысяч

долларов.

На основе приведенной выше предварительной оценки от-

ветьте, следует ли компании Triple X реализовать этот проект?

Решение

Определяем суммарные

издержки,

которые понесет компа-

ния,

решив реализовать данный проект:

Дополнительные постоянные издержки

Дополнительные затраты на оплату труда

Затраты на приобретение сырья

тыс. долл.

125 тыс. долл.

600 тыс. долл.

60 тыс.

долл.

Дополнительные накладные расходы

(0,12

х 500)

Суммарные производственные издержки 835 тыс. долл.

Теперь вычисляем стоимость выпуска единицы продукции:

835 000 „

пг

8,35 долл. на единицу.

Таким образом, наши вычисления показывают, что компа-

нии

Triple X следует продолжать закупать эту

деталь,

поскольку

производственные издержки на ее выпуск больше стоимости

закупки

на 0,1

доллара

на единицу продукции.