Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

302 THE HOMOGENEOUS MODEL CHAPTER 11

11.8 LINEAR TRANSFORMATIONS: MOTIONS

AND MORE

We have made ﬂats by explicit construction using points and directions, and incidence

operations among them. Once made, they can of course be moved around by transfor-

mations of the base space. If that space is Euclidean, we need to know how to perform the

Euclidean operations of translation and rotation to the ﬂats. In fact, it is often a conve-

nient way to construct an offset ﬂat by deﬁnining it ﬁrst at the origin and then rotating

and moving it to the proper location. That is, for instance, how we will interpret cam-

era images in Section 12.2, ﬁrst observing them in the camera fr ame, and then placing

the camera in its actual location to interpret the consequences in the world. Therefore we

need to know how to move ﬂats around, both in direct and in dual form.

We can also perform linear transformations on the homogeneous representation space

n+1

and inter pret the result they have on the elements in the base space R

. T his is a

representational trick, taking the representation space perhaps somewhat more seriously

than we should have. Still, we ﬁnd that in this way we can easily generate afﬁne and pro-

jective transformations of the base space, and since we get them virtually for free in this

manner, we may as well make use of that.

All this is an extension of common practice in the point-based homogeneous coordinates

approach. As before, the algebra dictates how to extend the deﬁnitions from points to

ﬂats as outermorphisms, and gives the general structural framework for these kinds of

transformations on general ﬂats.

11.8.1 LINEAR TRANSFORMATIONS ON BLADES

We repeat from Chapter 4 that linear t ransformations on blades can be extended as out-

ermorphisms, and therefore they follow simply from specifying what they do to a vector.

If x → f[x] foravectorx,thenforabladeX we have

X → f[X].

This makes transformations of offset subspaces very simple, at least when we have them

in their direct representation. If the offset subspaces are characterized as duals, the trans-

formation law is somewhat more involved, and we have derived that in Section 4.3.5. If

x → f[x] foravectorx, then a blade X

∗

(dually representing a subspace blade X) trans-

forms by the transformation f

∗

deﬁned as

∗

→ f

∗

] ≡ det (f)

−1

∗

]. (11.12)

We remind you that for an orthogonal transformation, f

∗

= det(f)f= ±f (see Sec-

tion 4.3.4).

SECTION 11.8 LINEAR TRANSFORMATIONS: MOTIONS AND MORE 303

11.8.2 TRANSLATIONS

Translations act on locations, not on directions. The vector space model had no clear

way to distinguish those except by giving them separate data structures, and that makes

translations in that model clumsy. A vector used as a position vector p translates to

p + t, whereas a vector used as direction translates to a. A line or plane could be char-

acterizedbyasupportvectord, which is yet another type of vector. This t ype should

translate only along itself to remain the support vector of the translated result: d trans-

lates to d + (t · d)/d. So in the vector space model, there are three ty pes of vectors, each

with their own translation law. The homogeneous model cleans all this up and makes the

translations of ﬂats automatic and universal.

The translation of a ﬂat X = p ∧ A should of course simply move it to (p + t) ∧ A, a ﬂat

with the same orientation but passing through the translated point p + t rather than p.

Since that adds t ∧ A to the original ﬂat X, we need to retrieve the direction A from X.

This is achieved as A = e

−1

X, and the translation formula becomes

translation : X →

[X] = X + t ∧ (e

−1

X).

(11.13)

This is clearly a linear transformation of X, since it consists of linear operations. Structural

exercise 15 has you prove that its determinant equals 1. This implies that translations do

not affect areas and volumes in the homogeneous representation space

n+1

, and since

they also do not affect normalization (for e

−1

X = e

−1

T

[X]), they preserve areas and

volumes in the base space

as well.

Note that (11.13) works on ﬂats of any grade, even for points with their scalar directions.

And it is consistent with our general representation: when we have made a ﬂat at the origin

with direction A (represented by the blade e

A), then we can get the general form of an

offset ﬂat by translating it over p to the point p:

A] = e

A + p ∧ A = p ∧ A.

Equation (11.13) is deﬁned for all blades, even though it was designed with ﬁnite sub-

spaces in mind. When we apply it to an improper subspace represented by the base space

blade X, we ﬁnd:

[X] = X,

so that directions are translation-invariant.

We also need to know the consequence of a translation on a dually represented offset ﬂat.

As we mentioned above, this is not the same as applying the original linear mapping

We denote the dual translation by

∗

, and compute it explicitly, by undualization of its

304 THE HOMOGENEOUS MODEL CHAPTER 11

argument, translation, and then redualization to get back to the dual representation. That

gives the dual translation formula:

∗

] ≡ (T

[X])

∗



X + t ∧ (e

−1

X)



∗

= X

∗

+ t(e

−1

∧ X

∗

)

= X

∗

− e

−1

∧ (tX

∗

(11.14)

You may verify that

∗

= T

−1

, in accordance with (11.12) for general linear transforma-

tions, since det(

) = 1.

We emphasize that the translation formulas apply to any blade (or dual blade), whatever

the grade. So there is no need for a separate translation operation for vectors, planes, and

so on. Yet there is a distinction between direct and dual representations, for

and T

∗

are

different functions of their arguments.

11.8.3 ROTATION AROUND THE ORIGIN

A Euclidean rotation around an axis through the origin characterized by a versor R should

affect the Euclidean positional and direction elements in the usual way: both should turn.

You might expect that we therefore need to decompose the ﬂat into these components,

do the rotation, and recompose. However, there is a nice surpr ise: since R commutes with

, we can make it act on the whole blade using the outermorphism property:

X = (e

+ p) ∧ A →

R[X] = (e

+ R p R

−1

) ∧ (R A R

−1

)

= (R (e

+ p) R

−1

) ∧ (R A R

−1

)

= R ((e

+ p) ∧ A) R

−1

= RXR

−1

This is a ver y convenient form, much nicer than the translation formula (11.13).

Dual representations of ﬂats can also be rotated. We can apply the procedure of undual-

ization of the argument, rotation, and redualization, but this results in the same rotation

formula, since the even versor R commutes with I

n+1

∗

→ (R (X

∗

n+1

) R

−1

) I

−1

n+1

= (R (X

∗

) R

−1

) I

n+1

−1

n+1

= R (X

∗

) R

−1

(Alternatively, you could have realized that for the orthogonal transformation

R, (11.12)

gives that

∗

= det(R)

−1

= R.) So a dually represented ﬂat can be rotated using the

same formula as for a directly represented ﬂat.

Here we see an advantage of oper ations that can be represented by even versors: they

transform elements universally, whether they are direct or dual. We will get back to this

issue; it is going to be an important feature of the conformal model.

SECTION 11.8 LINEAR TRANSFORMATIONS: MOTIONS AND MORE 305

11.8.4 GENERAL ROTATION

A general rotation around an axis at location t can be constructed in the usual manner by

translation over −t, rotating by R, and then putting the result back to t. This gives, after

some algebraic simpliﬁcation,

X → RXR

−1

+ (t − R t R

−1

) ∧



−1

(RXR

−1

)



It is clear that only the component of t in the rotation plane contributes, since t−R t R

−1

2(tR)R

−1

. You could see this formula as the translation of the rotation operator R, and

in that light, rotors transform differently from either blades or dual blades.

If X is a dual representative, the general rotation formula is different:

∗

→ RX

∗

−1

− e

−1

∧



(t − R t R

−1

)(RX

∗

−1

)



This difference is caused by the asymmetry of the translation operator.

11.8.5 RIGID BODY MOTION

Finally, the most common way of characterizing a rigid motion is as a rotation R around

the origin, followed by a translation over t. On a direct blade this obviously leads to

X → RXR

−1

+ t ∧



−1

(RXR

−1

)



and on a dual blade to

∗

→ RX

∗

−1

− e

−1

∧



t(RX

∗

−1

)



Those are all the formulas you will need for rigid body motions on general objects.

As you apply them to the speciﬁc factors, you will see that the purely Euclidean direc-

tions A are translation-invariant:

A → R A R

−1

+ t ∧



−1

(R A R

−1

)



= R A R

−1

This is consistent with their interpretation as improper ﬂats at inﬁnity: they cannot be

translated to the ﬁnite part of space.

11.8.6 CONSTRUCTING ELEMENTS THROUGH MOTIONS

If in an application you need a speciﬁc ﬂat and its representation, it is often convenient

to construct it ﬁrst at the origin, and then orient it and move it to the proper location.

For instance, to make a line through p, we start with some standard line in the direction

through the origin. This is represented by the blade e

∧ e

. Now apply a rotor R to

orient the line to the desired orientation u. Since Re



R = e

and R e



R = u, the result on

306 THE HOMOGENEOUS MODEL CHAPTER 11

∧ e

is e

∧ u: only the direction has changed. Now apply a translation T

to bring the

line to the proper location so that

] = p. The translation does not affect the direction

element, so that the result is the line p ∧u. Following these steps in terms of the operators

we just deﬁned shows that the general form of a line is indeed e

∧ u + p ∧ u. The same

reasoning to move a ﬂat at the origin with the correct orientation A to a desired location

gives e

∧ A + p ∧ A as its general form.

In this way of looking at the ﬂats, you see that the ﬁrst operation of orienting the ﬂat

correctly acts only on the direction element, and is therefore actually deﬁned in the vector

space model. The second step, translation, is the only one invoking the homogeneous

model, and it attaches itself only to the locational element e

, the point at the origin. In

this sense, the homogeneous model splits nicely:

[R[e

∧ A]] = T

] ∧ R[A],

and this clearly shows the backward compatibility of the attitudinal elements with the

vector space model. We have not lost any of our capabilities to compute with directions,

and added the locational aspects, in a neat algebraic extension.

11.8.7 RIGID BODY MOTION OUTERMORPHISMS AS MATRICES

The linearit y of the rigid body motions in the homogeneous model permits their repre-

sentation as matrices. The form of the matrices differs for the various elements they act

on, because the basis on which the points, lines, and planes are represented vary widely.

We will give these matrices explicitly for the 3-D case, in terms of the speciﬁc homoge-

neous coordinates of the points, lines, and planes, in Section 12.1.

11.8.8 AFFINE TRANSFORMATIONS

An afﬁne transformation is a special transformation of the points in the base space. It has

the property that it preserves colinearity of points on a line and the ratios of their distances

along that line. Any linear transformation of the vector space

has this property, and so

do translations.

That is the deﬁnition of afﬁne transformations in

, and we need to ﬁnd out what it

implies for their representation as mappings of

n+1

. As we have shown in Section 11.7.3,

the demand on meaningful ratios of distances of points along the same line implies that

their e

-coefﬁcient is preserved under afﬁne transformations. In formula, this means that

a point x transforms such that e

−1

· x is the same before the afﬁne transformation A as

after. Therefore,

−1

· x = e

−1

· A[x] =

A[e

−1

] · x.

Since this should hold for any vector x, an afﬁne transformation must satisfy

A[e

−1

] = e

−1

SECTION 11.8 LINEAR TRANSFORMATIONS: MOTIONS AND MORE 307

You may also read this as

A[e

] = e

, (11.15)

because e

−1

and e

only differ by a constant after you have chosen the metric.

It is easy to show that this implies that A preserves the

-subspace as being the part of

n+1

that is per pendicular to e

. We denote the pseudoscalar of R

as I

so that we can

wr ite the statement that no part of

has an e

component as

0 = e

−1

I

NowweapplyA to this statement and use the transformation property of the contraction

(4.13) to obtain

0 = A[e

−1

I

] =

−1

] A[I

] = e

−1

A[I

so that the transformed pseudoscalar indeed satisﬁes the same condition. Therefore the

afﬁnely transformed elements are still in

. In geometrical terms, the preservation of R

means that an afﬁne mapping changes directions into directions. More poetically, since the

directions are the elements at inﬁnity, afﬁne mappings preserve the heavenly sphere (not

point by point, but as a set).

We need to ﬁnd a standard form for the most general linear transformation A onavector

x of

n+1

whose adjoint preserves e

. It uses the most general linear transformation f in

the subspace

, and it can add an arbitrary vector t to translate the result. On a unit

vector x it should therefore have the effect A[x] = e

+ f[x] + t.Ifweextendf to R

n+1

by deﬁning f[e

] = e

, we can write this as A[x] = f[x] + t, but this is not yet a linear

transformation since it is not linear in the scale of x. The proper form must be

A[x] = f[x] + t ∧ (e

−1

· x),

where the factor on the t is the weight of the point x. When you try to extend this to

arbitrary blades as an outermorphism, you ﬁnd that this is awkward (some mixed terms

appear), until you realize that e

−1

· x = e

−1

·f[x] (do you realize why?). Then the afﬁne

transformation of a general multivector is

A[X] = f[X] + t ∧ (e

−1

f[X]).

(11.16)

Clearly the Euclidean motions are afﬁne transformations (rotations only have the f-part,

for translations that is the identity). But more transformations can be deﬁned; just tak-

ing out the translation component leaves the linear t ransformations in

, which can be

decomposed as rotations, translation, and nonuniform scaling.

The afﬁne combination of points in (11.2) is now clearly an afﬁne covariant, in the sense

that the afﬁne combination of transformed points equals the transform of the afﬁne com-

bination, as long as we use an afﬁne transformation. Afﬁne combinations of points can

308 THE HOMOGENEOUS MODEL CHAPTER 11

be combined using the construction operations such as outer product, meet, and join

to produce other afﬁnely covariant constructions. This is the algebraic and geometrical

basis of curve interpolation methods such as de Casteljau’s algorithm.

11.8.9 PROJECTIVE TRANSFORMATIONS

Projective transformations are the general linear transformations in the space R

n+1

interpreted in the space

. Such general transformations can transform ﬁnite points to

inﬁnite points (e.g., the rotation in

n+1

that turns e

into e

is among them).

Within the homogeneous model of geometric algebra, the projective transformations can

be extended as outermorphisms to act on all blades of

n+1

. In the base space R

, this

implies that we can not only transform points, but also offset subspaces such as lines and

planes. Therefore the point conic classically deﬁned through as the locus of all points x

satisfying the equation

x · A[x] = 0,

can easily be extended to a general conic

X A[X] = 0.

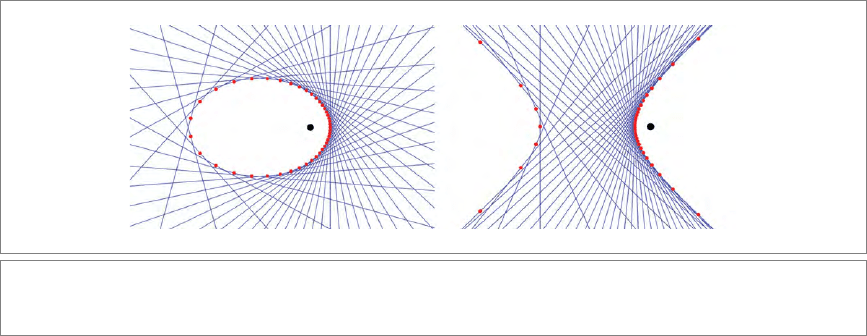
Figure 11.10 shows a line conic associated with a point conic in this manner.

Beyond this extended capability and its consequences, the geometric algebra of the homo-

geneous model so far has added little to the classical treatment of projective geometry.

Moreover, these capabilities are already present in the weaker Grassmann-Cayley algebra,

which is quite sufﬁcient to do nonmetric projective geometry in practice (as [21] shows).

Geometric algebra makes the incorporation of Euclidean measures in those techniques

somewhat easier, but that is about the extent of its contribution to date.

Figure 11.10: In the homogeneous model, the equation XA[X] = 0 can be solved for ﬂats of different grades. For points,

the solutions determine the familiar conics (in red); for lines, they give line conics (in blue).

SECTION 11.9 COORDINATE-FREE PARAMETERIZED CONSTRUCTIONS 309

On the other hand, geometric algebra changes our perspective on some aspects of

projective geometry. The principle of duality between points and lines in the plane, which

is classically presented as a unique feature of projective geometry, i s just a special case of

our usual dualization operation of division by the pseudoscalar. Not only is it applicable in

n-dimensions to elements of arbitrary grade, but it is a quantitative computational prin-

ciple rather than the merely qualitative substitutional symmetry of geometrical theorems

it often is in the classical t reatments. The full quantitative use of this principle is admit-

tedly a bit confused in the homogeneous model (as we show in Section 11.10), and that

has per haps led to an underestimation of its metric qualities. But dualization will come

into its own in the conformal model of Euclidean geometry. In that model, we will also

see how regular points in Euclidean geometry are actually point pairs (w ith one member

residing at inﬁnity), and that the identiﬁcation of opposite points in a spherical model of

projective geometry is again not uniquely projective, just a general fundamental principle

applied in a slightly different context (see Section 16.7.2).

Related to these issues is the suggestion that the homogeneous model may not be the

most natural representation of projective geometry. A geometric algebra representation

may be found in which conics can be represented as blades, and in which projective trans-

formations are rotors. Such a projective model would then be the natural way to embed

projective geometry within geometric algebra. It would be powerful: one should be able

to intersect two conics X and Y by their

meet Y

∗

X, for instance. The practical desir-

ability of similar computational techniques will be made apparent by our treatment of

the conformal model that provides this structure for Euclidean transformations. Having

such different geometries expressed in similar algebras will convey the common nature of

their fundamental structure.

To return to the homogeneous model, within the context of projective transformations

an afﬁne transformation amounts to choosing a particular pseudoscalar subspace I

and

demanding that it be an eigenblade that transforms to become a multiple of itself; the

complement e

is then preserved by the adjoint of the transformation. So afﬁne geometry

is projective geometry in a selected invariant base space of the homogeneous representa-

tion space.

11.9 COORDINATE-FREE PARAMETERIZED

CONSTRUCTIONS

The extension to blades and their operators that we achieved by considering the geometric

algebra of the homogeneous model can effectively be used in your programming. With

a bit of practice, you can design coordinate-free expressions for elements parameterized

by other elements. For instance, in 3-D you might have a line L and a point p not on it,

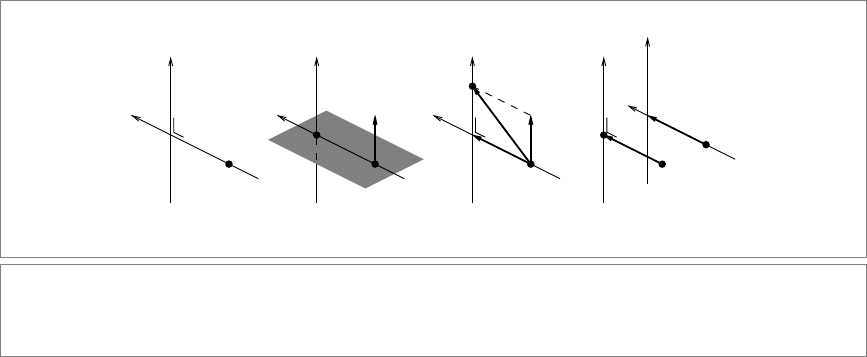
and wish to ﬁnd the line M through p that intersects L perpendicularly, as illustrated in

Figure 11.11(a).

310 THE HOMOGENEOUS MODEL CHAPTER 11

L⬘

(d)

(c)

(b)

(a)

Figure 11.11: (a) The problem: to ﬁnd the line M through a point p perpendicular to another line L . (b) A solution involving

the plane through p orthogonal to L to ﬁnd the support point c. (c) A solution using the rejection of the connection vector from

p to an arbitrary point q on the line. (d) Translating the situation back to the origin and solving it as a standard problem.

There are various routes to ﬁnding solution for such problems, some easier than others.

In the end you usually ﬁnd an expression that you could have written down immediately

had you looked at the problem in a better way from the start. Practice helps, and these

are clearly skills that you should develop if you have to use the homogeneous model a

lot. However, we will soon replace the homogeneous model by the conformal model as

an operational model of Euclidean geometry, which requires similar skills within a richer

set of metrical tools, so check Chapter 13 ﬁrst to see whether that model might not serve

your needs better.

Back to the problem of ﬁnding the line through p perpendicular to L. Let us denote the

direction of L by u (it can be found as u = e

−1

L), and the moment of L by U (it is

U = e

−1

(e

∧ L) ).

1. A number of thoughts arise about the relative geometrical situation of p, L, and

M, and it is interesting how they immediately invoke algebraic expressions in the

homogeneous model.

•

If we can ﬁnd the unit point c on L that is closest to p, then M = p ∧ c.

•

Whatever M is, it has to be perpendicular to L, and therefore it should be in

the plane Π though p that is perpendicular to L; that plane is, dually, Π

∗

p(u ∧ e

−1

) = −u + (p · u) e

, using (11.6).

•

Having the plane Π, the point c is its meet with L,soc =Π

∗

L.

The combination of these observations provides the solution for the closest point

c as c =



− u + (p · u) e

−1





u + U



= e

− uU + (p · u) u.ItgivesM as

p ∧ c. Done.

SECTION 11.9 COORDINATE-FREE PARAMETERIZED CONSTRUCTIONS 311

But we can learn from rewriting things. First, p ∧c can be rewritten as p ∧ (c −p) =

p∧(c−p), and now c−p can be simpliﬁed to c−p = −uU−(p∧u) u = (U−p∧u) u.

You should begin to recognize that ﬁnal expression. The moment U of L can be

constructed from a general point q on it as q ∧ u, and the 2-direction of M can

then apparently be written as ((q − p) ∧u) u, which is proportional to the rejection

((q−p)∧u)/u of the difference vector of any point on L with p, by the direction of L.

That is of course the support vector from p to L; now that we see it we recognize it

in the problem (see Figure 11.11(c)).

2. So in hindsight, our solution might have been: compute the support vector between

the unit point p and

and ar bitrary unit point q of L as the

rejection ((q − p) ∧u)/u,

and take the outer product with p to produce M. This is illustrated in

Figure 11.11(b). Using the original points q and p here saves extracting their

Euclidean parts, and makes it easier to express the result purely in terms of p and L.

We just use L = q ∧ u, and with u = e

−1

L obtain

M = p ∧

L − p ∧ (e

−1

L)

−1

L

Our computation in this way is even properly normalized: since p is a unit point,

M is weighted by the directed distance from p to L.Ifp is not a unit point, the

computation of the direction is incorrect, so a more robust expression would replace

p with p/( e

−1

· p) (at least in the direction part). Note that the normalization of L

cancels out, so L need not be nor malized.

3. Another way to ﬁnd the location c intersection point c is to realize that c ∧ u = L

since it lies on L, and that it lies on the same plane with normal u as p does, so that

c · u = p · u (alternatively, you could remark that c − p should be perpendicular

to u, giving the same equation). Then we add those to obtain c u = L + p · u, and

right division by u produces the result c =



L + (p · u)



/u. The line M is then

M = p ∧c = p ∧ (c −p) = p ∧



L −(p ∧u)



/u, giving the same result as above. Note

that this computation involves the geometric product in a direct algebraic manner

rather than invoking the

meet. It is the purest solution, algebraically speaking.

4. We may suddenly realize that the original question was merely to ask for the line

along the support vector of L when seen from p. So we should get the answer if we

translate L and p back to the origin (by a translation over −p), compute the support

of that translated line L



(which is a standard formula from Table 11.3), and translate

back to p, as illustrated in Figure 11.11(d).

Translating L over −p means adding −p∧u to it so that the moment of the translated

line is U − p ∧ u, with U the moment of L. The support vector of L



is then is

d = (U − p ∧ u)/u, which is the direction of M with proper sign and weight, so

M = p ∧ d. Or, to ﬁnish the computation properly, we must translate the support

line e

∧ d of L



back to the point p; then e

becomes p and the base space element

d is translation-invariant, so it remains d.