Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

332 APPLICATIONS OF THE HOMOGENEOUS MODEL CHAPTER 12

The dual representation of such a line is

∗

= L I

−1

= aI

+ m e

−1

, (12.6)

so it has the coefﬁcients {±m

, ± m

, a

} on the bivector basis, the

± sig ns are again determined by the metric chosen. Such a dual line is not in the

usual Pl

ucker coordinate tables, though we will soon see that it is convenient to have.

It should be clear that a mere coefﬁcient-based representation is dangerous and needs

to be accompanied by some bookkeeping, at the very least by maintaining separate data

structures (and this is presumably what the brackets are intended to remind us of). We

would be in favor of letting that bookkeeping be done by the algebraic tags on the coef-

ﬁcients; it is unambiguous, nonarbitrary, and computational. It is not necessarily more

expensive, for the multiplications of the basis blades used as tags are essentially Boolean

operations. We will expand on this in Chapter 19 for general geometric algebras.

12.1.3 COMBINING ELEMENTS

In interactions of elements, the explicit basis speciﬁcation takes care of the computational

rules for the Pl

ucker formula table. We g ive some examples to explain entries in the table,

and some that go beyond it, to show how the algebra empowers you to extend it if your

application so requires.

1. Plane through Point and Line. The formula for augmenting a point p by a line L

to make a plane is of course simply the outer product of point and the direct line

representation. Rewriting the result in terms of a 3-D cross product, we get

p ∧ L = (e

+ p) ∧ (a e

+ mI

) = e

∧ (mI

+ p ∧ a) + p ∧ (mI

)

= −(m + p × a) e

+ (p · m) I

So this is indeed the plane [a × p − m : m · p] listed in Table 12.1. That this should

be the natural extension of the construction of a line from two points is hard to

guess from the Pl

ucker table—yet it is a straightforward computation when one

remembers their embedding in the full algebra.

2. Point and Plane. To compute the

meet of a hyperplane Π and a point p in general

position, we need to compute by (5.8)

Π ∩ p = −p ∩ Π=−Π

∗

p = (n − δe

−1

)(e

+ p) = n · p − δ.

We recognize a scalar outcome, of which the geometry is the oriented distance

between point and hyperplane. This imbues scalars (grade 0 blades) with a geomet-

rical meaning: they are distances, and distances are apparently legitimate outcomes

of a coincidence operation.

This is of course the standard formula in the homogeneous model (calling this a

ucker coordinate formula is overdoing it), but is nice to see it as a standard

meet

rather than a special (albeit trivial) construct.

SECTION 12.1 HOMOGENEOUS PL

UCKER COORDINATES IN 3-D 333

3. Line and Plane.Themeet of a plane dually represented as Π

∗

= −n + δe

−1

and a

line L, in general position, is computed as

−Π ∩ L = −L ∩ Π=−Π

∗

L = (n − δe

−1

)(ae

+ mI

)

= (n · a)e

+ n(mI

) + δa + 0 = (n · a)e

+ (n ∧ m)I

+ δa

= (n · a)e

+ (m × n + δa)

Note how the orthogonality relationships between the basis elements automatically

kill the potential term involving δ and m.

This is the correct result, representing a point at the location (m × n + δa)/ (n · a)

in its homogeneous coordinates. It corresponds to the result in Table 12.1.

4. Skew Lines.The

meet of two lines L

and L

in general position (skew) is a measure

of their signed distance. We have seen this in algebraic form in (11.9). Here we redo

the computation compactly using the speciﬁc Pl

ucker coordinates with their alge-

braic tags:

∩ L

= L

∗

L

= (a

+ m

−1

)(a

+ m

) = −m

· a

− m

· a

Note that we used the dual line representation for one of the lines to derive this

compact expression quickly. Again, the basis orthogonality relationships have pre-

vented terms containing m

· m

or a

· a

from appearing (as they should!). If you

had any problems evaluating the expression (a

)(m

), use duality (twice) and

the commutation of the outer product of a vector and a bivector: (a

)(m

) =

((a

) ∧ m

= (m

∧ (a

))I

= (m

a

= −m

· a

The scalar result above retrieves the well-known compact Pl

ucker-based method

of determining how lines pass each other in space; three tests on the signs of such

quantities representing the edges of a triangle determine efﬁciently whether a ray

hits the inside of the triangle.

5. Intersecting Lines. When the parameters of the two lines L

= p

∧ a

and L

∧ a

satisfy a

∧ a

= 0 but (p

∧ a

) ∧ (p

∧ a

) = 0, then lines are not skew but

intersect (the latter condition implies (p

− p

) ∧ a

∧ a

= 0). The resulting meet

was given in (11.20); this is easily translated into Pl

ucker format as

∩ L

= a

× a



+ a

· (a

× a

) + a

· (a

× a

)

· m

− a

· m

)(a

× a

This outcome is immediately interpretable as a point; it is not one of the formulas

one usually ﬁnds in the Pl

ucker tables.

The other relationships of the table can be derived in a similar manner. If you need one

that is not in the table, you can now derive it yourself.

334 APPLICATIONS OF THE HOMOGENEOUS MODEL CHAPTER 12

12.1.4 MATRICES OF MOTIONS IN PL

UCKER COORDINATES

An afﬁne transformation A transforms a vector x to

A[x] = f[x] + t,

and it has to satisfy

A[e

] = e

to be afﬁne. We found in (11.16) that a gener al afﬁne

transformation of the base space

transforms a blade in the representation space

n+1

A[X] = f[X] + t ∧ (e

−1

f[X]),

where we conveniently deﬁne f[e

] = e

so that f can be extended to any blade.

We can now spell out the effects on the different elements of their Pl

ucker bases and write

the result again on that basis. If we then represent the elements by Pl

ucker coordinates,

the afﬁne transformation is representable as a matrix. By this transference principle, we

can easily compute the afﬁne matrices of some common transformations. We explain the

derivations, which you can relate to the result given in Table 12.2.

The point transformation is familiar, and a direct consequence of the deﬁnition. You can

compute its columns simply:

A[e

] = f[e

] + t = e

+ t, and A[e

] = f[e

The line transformation follows from the transformation of the elements of the line basis,

and is more involved:

A[e

∧ e

] = A[e

] ∧ A[e

] = f[e

] ∧ (e

+ t)

= f[e

∧ e

] − t ∧ f[e

]

= f[e

∧ e

] − (t × f[e

]) I

which in its matrix form involves the cross product matrix [[ t

]] . The other part of the

line transformation follows from results such as

A[e

] = f[e

I

] = f

−1

]f[I

] = det (f) f

−1

]I

The transformations for a dual line have not been speciﬁed in the table, but they are easily

made. Comparing (12.4) and (12.6), line dualization is achieved by the matrix



[[0]] ±[[1]]

[[1]] [[0]]



the sign choice again depending on the metric of the representation space. Using this

dualization matrix, any matrix for an operation on a dual line can be obtained from

SECTION 12.1 HOMOGENEOUS PL

UCKER COORDINATES IN 3-D 335

Table 12.2: Transformation of the ﬂats in the homogeneous model through matrices

constructed from the outermorphisms acting on their Pl

ucker coordinates. The same alge-

braic formula leads to quite different matrices. [[ t

]] is the matrix of a cross product, deﬁned

through [[ t

]] [[ x]] = [[ t × x]] . [[1]] is an identity matrix of appropriate size, [[0]] a zero matrix.

Element Point Line Plane

Basis (e

, e

)

, e

)

, e

, − e

)

Afﬁne



[[f]] [[ t]]

[[0]]





[[f]] [[0]]

−[[ t

]] [[f]] det(f)[[f]]

−T

 

det(f)[[f]]

−T

[[0]]

−[t]

det(f)[f]

−T

det(f)



Translation t



[[

1]] [[ t]]

[[0]]





[[

1]] [[0]]

−[[ t

]] [[ 1]]





[[

1]] [[0]]

−[[ t]]



Rotation R



[[

R]] [[0]]

[[0]]





[[

R]] [[ 0]]

[[

0]] [[ R]]





[[

R]] [[0]]

[[0]]



the operation A on a direct line by undualization, performing A, and dualization. This

transforms a matrix from acting on a direct line to acting on a dual line, according to



[[ A

]] [[ A

]]

[[ A

]] [[ A

]]



→



±[[ A

]] [[ A

]]

[[ A

]] ±[[ A

]]



In the plane transformation matrix acting on elements of the form [n, − δ], you may

recognize the 3 × 3 upper left submatrix as the tr ansformation of the normal vector from

(4.15). This also occurs in the direct representation of the plane, for the resulting coordi-

nates should undergo the same transformation whether they represent a direct plane or

a dual plane. You may derive it in the same manner as in its occurrence for line transfor-

mations, above.

336 APPLICATIONS OF THE HOMOGENEOUS MODEL CHAPTER 12

12.1.5 SPARSE USAGE OF THE 2

DIMENSIONS

The Pl

ucker coordinate representation and its associated matrices begin to show how an

implementation of geometric algebra can make use of the sparseness of the geometrically

signiﬁcant structures. In principle, the Clifford algebra of the 4-D representation space has

= 16 dimensions, and arbitrary linear transformations on this algebra would therefore

require 16×16 matrices, to be applied to a 16×1 vector, for some 2×16

= 512 operations

per transformation.

We have seen how the basic elements of 4-D geometry form subspaces of speciﬁc grades

1, 4, 6, 4, and 1. A linear transformation of the representation vector space (which is

4-D) leads to smaller matrices on each of those. This is already a reduction from 4, 096

operations to 1

= 346, saving a factor of 12. Of course, one invokes only

the transformation for the element at hand rather than transforming the whole ladder of

subspaces the worst case among these are the middle gr ades, which require some 216

operations for a general linear transformation.

Even among those linear transformations on the representational spaces, not all are equal,

for the extra dimension and the base space

have different semantics. Therefore, the

useful tr ansformations on the base space often have a special for m. In the afﬁne matrices

above, this is reﬂected by their sparseness; one block is always zero. This leads to some

additional reduction of the computational load.

We will go into the implementational issues in detail in Part III, after we have a more com-

plete view of how geometric algebra performs its Euclidean computations. The matrices

above will be found to play a role in fast implementations, and the consistent structure of

geometric algebra permits them to be constructed implicitly by an automatic code gen-

erator rather than having to be coded by hand.

12.2 IMAGING BY MULTIPLE CAMERAS

When you have multiple cameras observing the geometry of the world, the same points

or lines may be visible from several of them. If you know the relative positions and ori-

entations of the cameras, this allows a reconstruction of the 3-D event; alternatively, the

observed consistency can be used to estimate the camera parameters.

This geometr ical situation is well suited to analysis by the homogeneous model, since

it involves general points, lines, and planes. We do so in this section, retrieving classical

results in a coordinate-free and highly geometrical manner. (Some indices on symbols are

unavoidable, but they refer to the different cameras rather than to coordinates.)

As is usual when treating these issues, we simplify the situation geometrically by consid-

ering only ideal pinhole cameras, which p erform an ideal central projection.

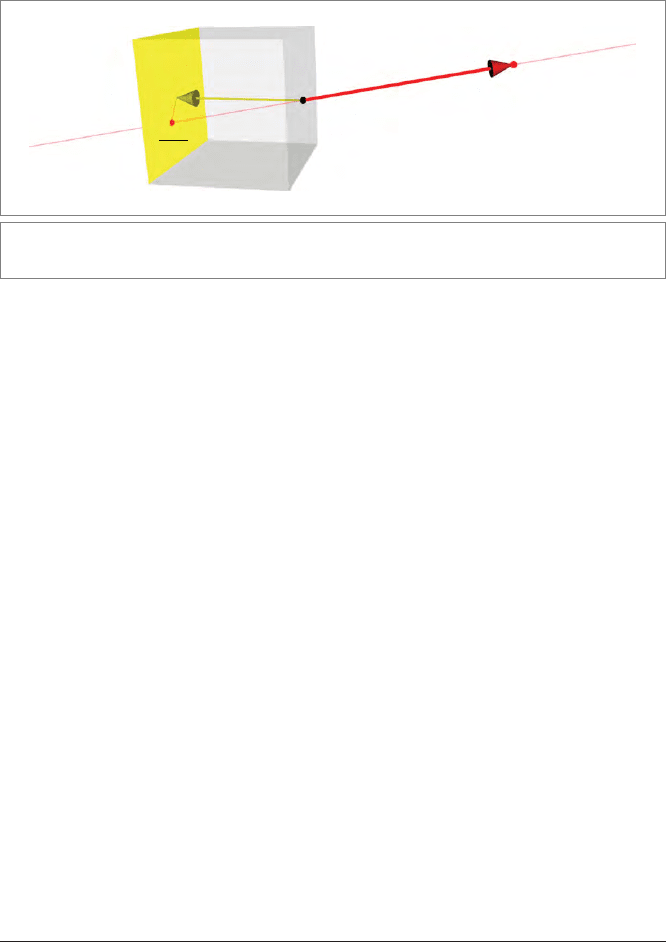
SECTION 12.2 IMAGING BY MULTIPLE CAMERAS 337

−

1 .

Figure 12.2: A pinhole camera.

12.2.1 THE PINHOLE CAMERA

Let us derive the formulas for the projection in a pinhole camera model using the

homogeneous model. We choose to denote the vectors from the pinhole, so the pinhole

itself is e

, the point at the origin.

The imaging plane of the pinhole is in a direction e, at a distance f. We can merge these

parameters f and e by saying that the support vector of the imaging plane is the vector f =

f e . The imaging plane Π itself is then dually denoted by Π

∗

≡ π = e

−1

− f

−1

. Verify this:

the equation x · π = 0 for a probe point x = e

+ x should lead to the Euclidean equation

x · f = f · f, showing that the f-component of the vector x has the correct magnitude to be

in the image plane.

If we now take an arbitrary unit point x in 3-D, the light ray from the pinhole to that

point is

L = e

∧ x = e

∧ x.

(12.7)

This deﬁnes x fully as the Euclidean coordinate of x relative to x, since the equation can

be solved as x = e

−1

∧ x). (This solution holds even when x has been given in homo-

geneous coordinates relative to a different origin; see structural exercise 2.) This shows

clearly that the point at x plays the role of the Euclidean direction x of the ray line. To

ﬁnd the projection formula of the vector x, we need to intersect this line with the imaging

plane. This is an instance of the

meet formula, and since we have the plane given dually,

it is easiest to use the inner product form of the

meet:

Π ∩ L = L ∩ Π=Π

∗

L = πL = (e

−1

− f

−1

)(e

∧ x) = e

−1

· x) + x.

(12.8)

1 The usual texts on imaging prevent awkward signs by imagining the imaging plane to be in front of the pinhole,

at a distance

f in the direction denoted by a unit vector e. We do not need to do so in our formulas, since the

intrinsic treatment of oriented elements in geometric algebra takes care of the signs automatically. You can take

f positive or negative, and the formulas still work to produce the projection onto the corresponding image plane.

338 APPLICATIONS OF THE HOMOGENEOUS MODEL CHAPTER 12

This is a point at the 3-D location



≡ P[x] =

−1

· x

, (12.9)

that is precisely the rescaling of x you would expect: the magnitude guarantees that



· f = f · f, so that x



indeed ends on the imaging plane. An interesting way of rewriting

this is explored in structural exercise 3.

The mapping that we have produced is nonlinear—already, the test of the linear scaling

property (which requires that αx should be mapped onto αx



) fails. However, if we stay

within the homogeneous domain and do not do the rescaling, the mapping is linear:

x → e

−1

· x) + x.

To get the mapping in terms of points rather than vectors, we substitute x = e

−1

∧ x),

and obtain

x → e



−1

− e

−1

) · x



+ x.

(12.10)

Alternatively, you can derive this by using L = e

∧ x instead of L = e

∧ x in (12.8). The

matrix of this linear transformation on the basis {e

, e

} is obtained by determining

the action on each of the basis vectors. For instance, e

→ e

−e

= 0; and e

→ e

−1

) + e

, so that the e

coordinate of the image of e

is f

−1

· e

. The other components are

similar, and the full mat rix becomes



[[1]] [[0]]

[[ f

−1

]]



familiar from the classical treatment (although that usually gives the matrix multiplied by

f, with e

as axis direction). In implementations, this is what you would use to act on

the homogeneous vectors, but the explicit algebraic form is more convenient for symbolic

simpliﬁcations.

In the classical way of using homogeneous coordinates, the linearity of the mapping is

already an advantage, certainly combined with the representation of rigid body motions

as linear transformations in the homogeneous coordinate representation. But the geo-

metric algebra treatment goes beyond this: not only is the transformation linear, it is also

an outermorphism. Therefore, combinations of the original objects using outer products

transform nicely (i.e., covariantly). In particular, spanning behaves well under the cen-

tral projection. The general projection of a homogeneously represented object X to the

imaging plane is simply always the meet of e

∧ X with the image plane Π:

X → (e

−1

− f

−1

)(e

∧ X) = e

∧



−1

− e

−1

) X



+ X.

You can show, by analogy to the above, that this results in a ﬂat with direction

D = e

−1

(e

∧ (f

−1

X )) and support point (e

−1

e

∧ X)/D.

SECTION 12.2 IMAGING BY MULTIPLE CAMERAS 339

Lines can now be projected immediately. On the Pl

ucker line basis of (12.5), the projection

is represented by the matrix



[[0]] [[f

−1

]]

[[0]] [[1]]



(12.11)

which is derived by techniques similar to our derivation of the matrices in Table 12.2. The

projection of a general plane is not very interesting, since all planes project to the image

plane by the matrix



[[0]] −[[ f

−1

]]

[[0]]

[[1]]



Of course, in the homogeneous model of geometric algebra, we also have the rigid body

motions present as linear transformations and their outermorphisms, so the whole frame-

work now contains everything of interest in a consistent manner.

12.2.2 HOMOGENEOUS COORDINATES AS IMAGING

Two points spanning a line in the world generate a projected line in the image plane

spanned by two projected points. It is an amusing (but rather confusing) property of

the homogeneous model that homogeneous coordinates can be introduced in the image

plane using the support vector f as the extra homogeneous embedding dimension. Let

us consider a camera or focal length equal to 1, and focal vector f. We will denote points

in the image plane relative to the optical center (the location f) by an underscore. Then

a point at image location x

is seen from the pinhole as f + x.Itgeneratesarayofpos-

sible real-world positions e

∧ (f + x). The line spanned by two image points could be

constructed in two ways, which are indeed consistent:

•

The two rays e

∧(f+x) and e

∧(f+y) together span a world plane e

∧(f+x)∧(f+y),

and this plane cuts the image plane in the world line

−1

− f

−1

)(e

∧ (f + x) ∧ (f + y)) =

= e

∧ (y − x) + (f + x ) ∧ (f + y)

= (e

+ f + x

) ∧ (y − x).

We see from the ﬁnal form (compare (11.3)) that this is a line in the direction (y

−x)

passing through the point f+x

of the world (which is the point x on the image plane).

This is of course what we would expect.

•

Directly taking the outer product of the two points in the image plane gives

(f + x

) ∧ (f + y) = (f + x) ∧ (y − x).

If we are to interpret this as the line through the image points at x

and y, then clearly

f plays the role of the homogeneous coordinate in (11.3).

340 APPLICATIONS OF THE HOMOGENEOUS MODEL CHAPTER 12

The similarity of the two approaches is apparent and generalizes to higher dimensions.

Taking a slightly philosophical excursion, working in homogeneous coordinates is like

viewing the 3-D world through a pinhole in a 4-D camera. Homogeneous coordinates

are a useful version of Plato’s cave metaphor, where the 3-D shadows of a 4-D higher

reality are what we experience, but in which there is a clear mathematical advantage to

use the 4-D “ideal world” as our spatial representation. With homogeneous coordinates,

this metaphor can be taken literally as a projection from 4-D to 3-D.

12.2.3 CAMERAS AND STEREO VISION

When working with cameras, one often measures positions in the local coordinate system

of the camer a. In that case, the use of coordinates is essential for the conversions to objec-

tive world coordinates for comparison with other camera measurements. So even though

geometric algebra is coordinate-free in a way that linear algebra is not, we still need coor-

dinate transformations for common geometrical tasks.

Let us look at a single camera. Its position and orientation can be characterized rela-

tive to a standard p osition and orientation, at the origin e

looking in the fe

-direction

(where f is the focal length). Any general rigid body transformation can be performed as

a pure rotation around the origin, followed by a translation. Let us denote the composite

transformation by A[·]. In the homogeneous coordinate representation, it is linear and an

outermorphism.

To be speciﬁc, consider a camera oriented by R

(so that R

[fe

] = f) and its pinhole at

the point a = e

+ a. This deﬁnes A as

X → A[X] = R

[X] + a ∧ (e

−1

R

[X]).

(12.12)

If we measure a point in the image of camera A at location x

(which for now we take to

be converted to millimeters on the image plane after processing using the internal camera

parameters), then this is a vector having the direction x = fe

+ x in the local coordinate

system. Also in that system, it determines the line e

∧ x emanating from the pinhole. This

line can be converted to world coordinates by applying A, which you may either see as a

coordinate transformation or as moving the camera to its actual conﬁguration:

A[e

∧ x] = A[e

] ∧ A[x] = (e

+ a) ∧ R

[x].

Here we applied the outermorphism A to each of the factors in the outer product. We

wrote the result on e

as a translation characterized by the position vector a and its

effect on the purely directional element x as a rotation R

. Both are easy consequences

of (12.12).

Introducing a second camera B, we have a similar equation generating a line B[e

∧ x

]

from the observation x

(or x

) and the rigid body motion B. If those two cameras are

looking at the same point x and we know their relative positions and attitudes, then the

SECTION 12.2 IMAGING BY MULTIPLE CAMERAS 341

measurements x

and x

(or rather x

and x

) are not geometrically independent. There

is a linear constraint relating them, known as the epipolar constraint, which arises from

the fact that the two 3-D lines we have constructed should intersect in the point x.

For this to happen, the

meet of the two lines should be degenerate, which happens when

their na

ïve join (computed as an outer product) is zero:

0 = A[e

∧ x

] ∧ B[e

∧ x

Because A and B are outermorphisms, we can manipulate this equation to a more familiar

form. First distribute the mappings over the outer products:

0 = A[e

] ∧ A[x

] ∧ B[e

] ∧ B[x

] = (e

+ a) ∧ R

] ∧ (e

+ b) ∧ R

Taking the inner product of this equation with e

−1

, and noting that the second and fourth

factor are purely Euclidean (so that they do not contribute), we get

0 = R

] ∧ (e

+ b) ∧ R

] + (e

+ a) ∧ R

] ∧ R

]

= R

] ∧ (b − a) ∧ R

The meaning of the resulting equation is sketched in Figure 12.3: the observed vectors and

the relative camera position are in one plane. (If in the derivation the idea of taking the

inner product with e

−1

strikes you as unnatural, you can also write out the above equation

in its Euclidean and non-Euclidean components, and focus on the non-Euclidean part

being zero—that is, the same. The Euclidean part is then automatically zero, so we have

not lost generality.)

The equation above is often rewritten in terms of the relative rotation of B relative to A,

which is R

≡ R

−1

. This gives, applying R

−1

to the whole blade equation:

0 = x

∧ R

−1

[b − a] ∧ R

We recognize in R

−1

[b − a] the position of the pinhole of B measured in the A-frame.

Denoting that as the translation vector t

,weget

0 = x

∧ t

∧ R

(12.13)

This is the epipolar constraint on the point x

given the point x

(in B coordinates) and

the relative poses of the cameras.

Note that this equation states that the measured x

should lie on the 2-blade t

∧ R

]

parameterized by x

. In the image plane, this implies that the point x

lies on the line

∧ R

+ x

]—note now e

plays the role of a homogeneous model dimension for

the image plane, just as we showed before.