Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

312 THE HOMOGENEOUS MODEL CHAPTER 11

Whenever you solve a problem that is important to a computation, try to derive and inter-

pret the result in several ways. Some of those may integrate better with other aspects

of the larger problem and allow for a more efﬁcient combined total solution. Make

sure you use the opportunities that the homogeneous model offers to give your results

quantitative properties with useful signs and weights; related to that, check that the for-

mulas you derive are robust to normalization assumptions.

11.10 METRIC PRODUCTS IN THE HOMOGENEOUS

MODEL

You may have noticed that we have been rather careful in our choice of algebr aic

operations. In fact, there is hardly more than the outer product, duality, the

meet, and

outermorphisms involved on the elements of the representation space

n+1

.Whenyou

realize that mathematicians can introduce duality in a nonmetric way (by employing

k-forms), you see that these are all nonmetric operations. The

meet is simply the dual

of the outer product of duals, and we have seen in Chapter 5 that its outcome does not

depend on a metric.

When we did use the purely metric products of contraction or the geometric product, it

was either on the subspace

or on elements with the same ﬂat in R

n+1

,suchaswhen

computing the cross ratio. (The probing of a dual representation by the inner product

with a point can also be written nonmetrically using a 1-form, so it does not count as

metric usage).

Our nonmetrical use of the homogeneous model

n+1

is in fact most clearly demon-

strated by our refusal to even choose its metric: we purposely left the option of choosing

= 1 or e

= −1. That did not return to haunt us in our results so far, which must

therefore have b een nonmetrical.

The main problem with using the metric of

n+1

is that you cannot use it directly to do

Euclidean geometry, for it has no clear Euclidean interpretation. We address this funda-

mental shortcoming because it helps reﬁne what the properties of a model of a geometry

should be. That understanding prepares us for the conformal model that ﬁxes the awk-

wardness of the homogeneous model in this respect.

11.10.1 NON-EUCLIDEAN RESULTS

We would demand of a representation for Euclidean geometry that it is structure-

preserving under translations (i.e., tr anslation-covariant). This means that a result that

holds in one location can be translated to another location and still hold. (We also demand

rotation covariance, but the homogeneous model inherits that property from the vector

space model, so we need not discuss it.) Translation covariance should imply that we can

take another point e



= e

+ t as our new origin instead of e

, and all geometrical results

SECTION 11.10 METRIC PRODUCTS IN THE HOMOGENEOUS MODEL 313

relative to this new origin should be similar. Yet this change of origin from e

to e



changes

the metric of

n+1

, for



)

= e

+ t

and whether we choose e

=+1 or e

= −1, the square of e



is going to be different.

This deﬁciency also shows itself in the geometric product, and propagates to versors.

Things get structurally awkward with inverses, for the inverse of the representation is not

the representation of the inverse. This statement is

−1

= (e

+ x)

−1

+ x

= e

+ x/x

= e

+ x

−1

and you see how different the results are. (An element that does frequently occur when

computing with inverses is e

−1

− x

−1

. It has the property (e

−1

− x

−1

) · (e

+ x) = 0

and is therefore some standard perpendicular direction to the vector x, useful in duality

computations.)

The lack of well-behaved inverses haunts the use of the geometric product in versor con-

structions. For instance, the reﬂection of one point into another seems proper enough at

the origin:

−1

= e

+ p) e

−1

= e

− p.

That is a reasonable geometric outcome, a point reﬂection has clearly taken place. But

when we use another point as reﬂector, something strange happens. Let us study that

around the origin as well:

−1

= (e

+ q) e

+ q)/(e

+ q

)



− q

) + 2 e



/(e

+ q

This is a weighted point at location

− q

Not only is this strangely nonlinear, but it depends on the metric of the representation

space since it contains e

. We saw above that this metric depends on where the origin

is. This well-deﬁned reﬂection construction in

n+1

may be useful for something (it is

related to stereographic projection), but it is not meaningful for the Euclidean geometry

These insights are not new. In the classical use of homogeneous coordinates, you should

have learned to be careful with the inner product. The inner product of two vector repre-

sentatives x and y is

x · y = e

+ x · y,

and only the second term has objective meaning for the computation of angles and lengths

in the Euclidean space you are modeling. But that quantity might as well have been com-

puted using only the vector space model. On the other hand, the inner product does have

314 THE HOMOGENEOUS MODEL CHAPTER 11

a sensible meaning when deﬁning a plane in a dual manner by π = n − e

−1

δ,aswe

have seen:

x · π = 0 ⇐⇒ x · n = δ.

This is essentially a nonmetric use of the inner product, since it is done between a direct

element and a dual element: 0 = x · π = x · Π

∗

= (x ∧ Π)

∗

. It is all a bit confusing

and less tidy than you might have hoped from geometric algebra. We emphasize that the

problem is not geometric algebra itself, but the homogeneous model and our desire to

use it for Euclidean geometry. It will be replaced by a much better model for that purpose

in Chapter 13.

11.10.2 NONMETRIC ORTHOGONAL PROJECTION

Despite its metr ic shortcomings, we can learn interesting geometry from the structure we

have in the homogeneous model. As an example, let us look at orthogonal projection. In

Part I we derived that the projection of a blade X onto a blade A is represented as

[X] = (XA)A

−1

The result is in A in a manner that in a Euclidean space is “orthogonally below X.” You

would expect this to be a metric construction.

The algebraic operation can be performed in the homogeneous model as well, for inverses

are well-deﬁned. What can this orthogonal projection mean in a space

n+1

without

a clear metric? The homogeneous projection of a p oint x onto a line L is depicted in

Figure 11.12. The result is a point on the line L with an unexpected relationship to its

dual: the line x ∧ P

[x] intersects the dual line L

−∗

It turns out that we can rewrite the projection as a

meet, not only in the homogeneous

model, but in general. Leaving out the inverse of A to show the structure of the derivation

more clearly, and assuming X and A in general position, we simply rewrite:

A ∩ (X ∧ A

−∗

) = (X ∧ A

−∗

)

∗

A = (XA)A.

(11.17)

The orthogonal projection is therefore less metric than we might have assumed, though

it does involve an (inverse) dual.

To explain Figure 11.12, the projection in 3-D of a point x on a unit line L is obtained by

making the dual L

−∗

. This is also a line, and writing L as L = (e

+d) u = e

u+M,weﬁnd

−∗

= −e

−1

夹

− u

夹

). This has 1/d as its support vector, and runs perpendicular to

the plane through L and the origin; both properties are of course very much dependent on

the location of the origin. Then the projection is the point of L obtained by intersection

with the plane x ∧ L

−∗

. That also implies that the line through x and its projection cuts

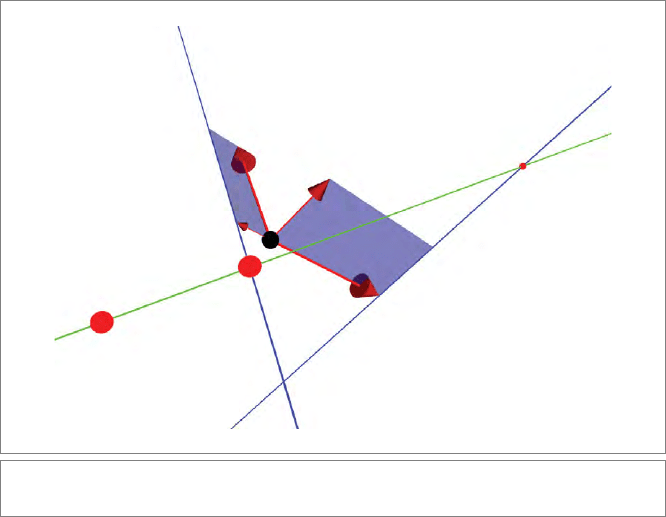
SECTION 11.11 FURTHER READING 315

⎦

L)/L

−

Figure 11.12: The orthogonal projection in the homogeneous model (see text).

−∗

. T his situation is depicted in Figure 11.12. Euclidean geometry it ain’t, but it could

be useful in projective geometry.

11.11 FURTHER READING

A good reference for getting an intuition for oriented subspaces in the homogeneous

model is Stolﬁ’s classical book [60]. His hand-drawn visualizations are justly famous, and

they give several ways of looking at this “raylike” representation of points in one more

dimension.

He uses a kind of Grassmann algebra to encode the basic operations between ﬂats, but

grounded in

meet and join rather than the outer product and the contraction. That is

more limiting for use in Euclidean situations, so that his treatment is mostly nonmetric,

not even reverting to the vector space model where this would have been possible. This

is typical of most uses of the homogeneous model in projective imaging as well. Some

references for that ﬁeld are given at the end of the next chapter.

316 THE HOMOGENEOUS MODEL CHAPTER 11

11.12 EXERCISES

11.12.1 DRILLS

Compute the 2-blades corresponding to the lines given by the data below. Which of the

lines are the same, considered as weighted oriented elements of geometry, and which are

the same as offset subspaces?

1. Two points at locations e

and e

2. A point at location e

and a direction (e

− e

3. A point at location e

and a direction (e

− e

4. Two points with locations 2(e

− e

) and 3(e

− e

5. A point at location e

and a direction 2(e

− e

6. A unit point at location e

and a point with weight 2 at location e

11.12.2 STRUCTURAL EXERCISES

1. Let an orthonormal coordinate system {e

}

i=1

be given in 3-D Euclidean space.

Compute the support vector of the line with direction u = e

+ 2e

− e

, through

the point p = e

− 3e

. What is the distance of the line to the origin?

2. Convert the line of the previous exercise into a parametric equation x = p + λ u;

express λ as a function of x forapointx on the line. Interpret geometrically.

3. Show that the support vector d of a k-ﬂat is the rejection of the position vector of

an arbitrary point p on it by the k-direction A.

4. Show that the weight of the plane p ∧ q ∧ r is twice the area of the triangle

spanned by the normalized points p, q, and r. Give the corresponding statement for

a general (k − 1)-dimensional ﬂat constructed from k normalized points (see also

Section 2.8.3).

5. Three points a, b, c form a plane, and these points can be used to address any other

point x in that plane as a linear combination:

x = α a + β b + γc.

Using normalized points, one can do this with an afﬁne combination. The resulting

scalars α, β, γ are called barycentric coordinates (literally, “weight-based”). Compute

α, β, γ in terms of the points a, b, c, and express the result using the relative vectors

a = a

− c, b = b − c and x = x − c.

This

should give you:

α =

x ∧ b

a ∧ b

, β =

x ∧ a

b ∧ a

, γ = 1 −

x ∧ (b − a)

a ∧ b

. (11.18)

Interpret the result geometrically in terms of areas in the plane (most easily seen

when x is inside the triangle formed by a, b, and c). What are the barycentric coor-

dinates of the center of gravity?

SECTION11.12 EXERCISES 317

These bar ycentric coordinates can be used to interpolate any scalar property ␾ given

at each of the vertices of a triangle to an intermediate ␾

value at x, through:

␾

= α ␾

+ β ␾

+ γ ␾

(11.19)

This equation will be used in the ray tracer of Chapter 23.

6. The inverse of the support vector of a plane spanned by three points at locations p,

q, and r is equal to the sum of the reciprocal vectors corresponding to these three

vectors in their own frame {p,q,r}. Show this using (11.4) and (3.31).

7. In the paramet ric equation for an offset ﬂat (11.5), the vector x determines the val-

ues of the λ

uniquely. Compute a formula for λ

. (Hint: Eliminate the other λ

, with

j = i, by suitably chosen outer products with a

vectors. Alternatively, use the idea

of a reciprocal basis from Section 3.8.)

8. The base space

is a subspace of R

n+1

, and it has a subalgebra of the geometric

algebra of that full space. Hestenes [27] has devised the projective split relativetoa

ﬁxed element to express a subalgebra of a space in standard form. Using e

and e

−1

(the elements of R

n+1

that are not also in R

), a direct blade of R

n+1

can be split by

his method. This leads to a natural factorization of the blade. The following does

this, and results in the familiar parts that we recognize as support and direction (see

also Table 11.3).

X = e

−1

= e

∧ (e

−1

X) + e

(e

−1

∧ X)

= e

−1

X) +

−1

(e

∧ X)

−1

X

−1

X)ife

−1

X = 0



−1

(e

∧ X)

−1

X



−1

X)ife

−1

X = 0

Perform a similar split for the dual blade to derive the corresponding column of

Table 11.3.

9. Construct the dual representation of the midplane between two points p and q.

10. We suggested in Section 11.7 that the

meet of two points p and q on a line L = d u

is proportional to their distance. Explore precisely how, so give p ∩q quantitatively.

11. The

meet of two skew lines p ∧ u and q ∧ v can be computed as M

∗

L. Verify the

steps in the following derivation of (11.9) using this formula.

(p ∧ u) ∩ (q ∧ v) =



(q ∧ v)(I

−1

∧ e

−1

)



(p ∧ u)



q(vI

−1

∧ e

−1

)



(p ∧ u)



q(vI

−1

) ∧ e

−1

+ (vI

−1

)



(p ∧ u)



q(vI

−1

)



u + (v I

−1

)(p ∧ u)

318 THE HOMOGENEOUS MODEL CHAPTER 11

= u



q(vI

−1

)



+ (p ∧ u)(vI

−1

)

= (u ∧ q ∧ v)I

−1

+ (p ∧ u ∧ v)I

−1



(p − q) ∧ u ∧ v



I

−1

12. Take two lines L

= p

∧a

and L

= p

∧a

that satisfy a

∧a

= 0 but (p

∧a

) ∧

∧ a

) = 0. These lines are not skew, but intersect in some plane in space. Their

join is now proportional to the common plane a

∧ p

∧ a

= p

∧ a

. Let the

unit blade representing this be I. Show that their

meet is now:

J = I (proportional to p

∧ a

)

(11.20)

M = e

∧ a

)



+ a

∧ a

)



− a

∧ a

)



((p

+ p

) ∧ a

∧ a

)/I

with duality relative to I

, the unit blade of a

∧ a

(i.e., as XI

−1

whether or not

X is in I

). Interpret the result, and show its geometric meaning by relating it to

the special case of (11.8) (where the common plane passed through the origin). In

that case, the inner products could be replaced by geometric products, and you may

recognize Cramer’s rule (since the ratios of areas in the same plane are ratios of 2-D

determinants). This {a

}-basis is a natural coordinate system for this problem in

the Euclidean plane. In 3-D, this is extended by the last term, which is perpendicular

to the common plane (for it is in fact a rejection).

The proportionality factor α = (a

∧ a

)



of e

in the expression for M is the weig ht

of the point at d. It indicates the numerical stability of the intersection, and may be

used as a measure of the signiﬁcance of the interpretation as an intersection point.

13. In Section 11.7.2, we stated, “In a plane with counterclockwise orientation, the pos-

itive side of the line is on your left when you look along its direction.” Convince

yourself that this statement gives the same positive side independent of whether you

look at the plane from above or below, so that it is a truly geometrically invariant

deﬁnition. That is good, for it would be useless otherwise.

14. Translate the representational space e

, both in its direct representation and in its

dual representation. Do the algebraic results match your geometric expectation?

15. Show explicitly that the determinants of the translation formulas (11.13) and

(11.14) for a ﬂat and for a dual ﬂat both equal 1.

16. Showexplicitlythattranslationisan outermorphism; thatis,

[X]∧T

[Y] = T

[X ∧Y].

(Hint: You will ﬁnd that this holds because of the sign changes in the dist ributive

formula for the contraction (3.10).)

17. There is a way to patch up the homogeneous model so that translation becomes

representable in a versor-like form, and you may ﬁnd this used in the somewhat

older literature (such as [4]). It uses a different metric in which e

· e

= 0, and

represents a point at location x as x = 1 + xI

,whereI

= e

is the pseudoscalar

of the homogeneous representation space. Show that in this approach, the element

T = (1 + tI

/2) acts more or less as a translation versor on points, in the sense that

T x T is the translated point (note the absence of the reversion!).

SECTION11.12 EXERCISES 319

However, the representation of the higher-grade objects (such as lines and planes)

in such a model is ad hoc, in that various objects are not related to each other by an

outer product-like spanning operation, or a meet-like product for intersection.

Work out some cases and show that the versor form of the translation is not

perfect: some objects should be translated as TX



T, others as TXT, whereas one

would have hoped that such fundamental operations would be independent of

their argument.

Since the invention of the conformal model of Chapter 13 (which ﬁxes all these

defects by using null vectors in a different manner), this motor algebra has fallen

into disuse, and we mention it here only for completeness.

18. Setting the cross ratio deﬁned in (11.11) to λ, show that by permutations of the

points p, q, r, s you can obtain any of λ, 1/λ, (1 − λ), (1 − 1/λ), 1/(1 − λ) or

1/(1 − 1/λ)). These are permutation symmetries that you should take into account

when checking the similar situation of four unlabeled points (or lines) before and

after projective transformations. You can make a symmetrical function of them all

as a test for equality of situations: (λ

− λ + 1)

/(λ(λ − 1))

; see [55].

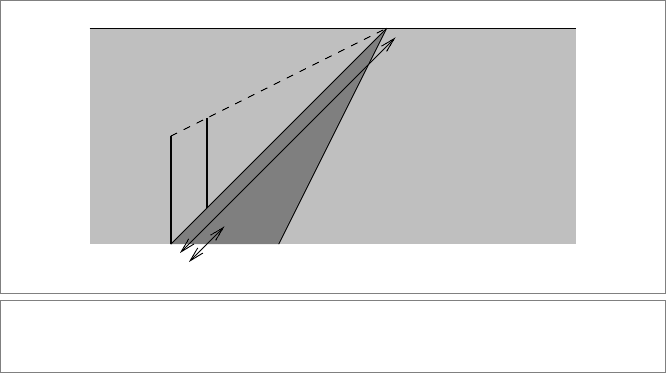
19. You are to draw a sequence of equidistant telegraph poles along a st raight road in

a picture showing the landscape seen in a bird’s eye view, with the horizon 6 cm

from the ﬁrst pole and the separation between ﬁrst and second pole 1 cm (see

Figure 11.13). Compute where the third pole should be. Extend this to comput-

ing the location of the kth pole. (Hint: Compute the cross ratio of the ﬁrst two poles

to the point at inﬁnity in a “straight” photograph. Then realize that the cross ratio

is a projective invariant.)

20. In the homogeneous coordinate approach, an afﬁne transfor mation A is repre-

sented by a matrix acting on the homogeneous coordinate representation of a vector

6 cm

1 cm

Figure 11.13: The beginning of a line of equidistant telegraph poles. Structural exercise

19 asks you to draw the rest.

320 THE HOMOGENEOUS MODEL CHAPTER 11

[[ x

,1]]

. Interpret the deﬁning condition A[e

] = e

of (11.15) in terms of a

property of such an afﬁne matrix. Conﬁrm your answer in Table 12.2.

21. Redo some of the orthogonal projection examples in the vector space model of a

3-D Euclidean space using the

meet interpretation of (11.17).

11.13 PROGRAMMING EXAMPLES AND EXERCISES

In the GA sandbox source code package, the implementation of the homogeneous model

of 3-D Euclidean space is called

h3ga. The basis vectors are e1, e2, e3, and e0. The metric

is Euclidean (i.e., e

· e

= e

· e

= e

· e

= e

· e

= 1). Various specialized multi-

vector types of blades are available, as dictated by our interpretation of the algebra (see

Table 11.4).

Note in this table that

bivector and lineAtInfinity are basically the same ty pes; only

their names differ.

Gaigen 2 has no problem with this.

An outermorphism class (

om) is also available. The specialized outermorphism class

omPoint can be applied to points only; it is the equivalent of a classic 4 × 4 homoge-

neous matrix. This is demonstrated in Section 12.5.1.

11.13.1 WORKING WITH POINTS

Our ﬁrst foray into programming with the homogeneous model is an experiment with

drawing and translating points. Two types of points are provided in

h3ga: the point class

and the

normalizedPoint class. The e0 coordinate of a normalizedPoint is always 1,so

only normalized points can be stored in it.

normalizedPoint variables do not store their

Table 11.4: Specialized multivector types in the h3ga.

Name Sum of Basis Blades

vector e1, e2, e3

point e1, e2, e3, e0

normalizedPoint e1, e2, e3, e0=1

line e1∧e2, e2∧e3, e3∧e1, e1∧e0, e2∧e0, e3∧e0

lineAtInfinity e1∧e2, e2∧e3, e3∧e1

bivector e1∧e2, e2∧e3, e3∧e1

plane e1∧e2∧e3, e1∧e2∧e0, e2∧e3∧e0, e3∧e1∧e0

planeAtInfinity e1∧e2∧e3

rotor scalar, e1∧e2, e2∧e3, e3∧e1

SECTION11.13 PROGRAMMING EXAMPLES AND EXERCISES 321

e0 coordinate; this saves one coordinate and is also more efﬁcient during computations.

So a

point has 4 coordinates, a normalizedPoint only 3.

Since OpenGL is internally based on homogeneous coordinates, the homogeneous model

is in many aspects a perfect match for it. Accordingly, both types of points can easily be

used as vertices in OpenGL, as shown below.

The example code draws two triangles. You can manipulate the vertices of the triangles

with the mouse. One triangle is made up from

points, the other from normalized-

Points

. The code to draw the t riangles with points is

glBegin(GL_LINE_LOOP);

for (int i = 0; i < NB_POINTS; i++) {

const point &P = g_points[i];

glVertex4fv(P.getC(point_e1_e2_e3_e0));

// or:

// glVertex4f(P.e1(), P.e2(), P.e3(), P.e0());

}

glEnd();

Note that we use glVertex4fv() to pass an arr ay containing all 4 coordinates in OpenGL.

These are the e

, e

, and e

coordinates, or—in OpenGL terminology—the x, y, z,

and w coordinates. Alternatively, we could use

glVertex4f() and pass each coordinate

separately, as shown in the line that is commented out.

To l o a d

normalizedPoints in OpenGL, glVertex3fv() is used:

glBegin(GL_LINE_LOOP);

for (int i = 0; i < NB_NORMALIZED_POINTS; i++) {

const normalizedPoint &P = g_normalizedPoints[i];

glVertex3fv(P.getC(normalizedPoint_e1_e2_e3_e0f1_0));

//note e0 ’fixed’ at 1.0

// or:

// glVertex3f(P.e1(), P.e2(), P.e3());

}

glEnd();

Since both the normalizedPoint type and OpenGL assume that the e

coordinate is 1,

this works as expected.

Translation of the points is implemented using the generic translation formula of (11.13).

g_points[idx] = _point(g_points[idx] + (T ^ (e0 << g_points[idx])));

where T is the translation vector. The possible weight of the points is taken into

account automatically. In the case of

normalizedPoints, the left contraction (e0 <<

points[g dragPoint]) is evaluated at compile time, and has no run-time cost. That

is, the following code

g_normalizedPoints[idx] =

_normalizedPoint(g_normalizedPoints[idx] +

(T ^ (e0 << g_normalizedPoints[idx])));