Джумадильдаев А.С. Элементы дискретной математики (часть 1)
Подождите немного. Документ загружается.


• Z
• Z
• Q
• Q
• Q \{0}
• R ◦ a ◦ b = a + b +2.
• R \{−1}
◦ a ◦b = a + b + ab.
•
S
3
.
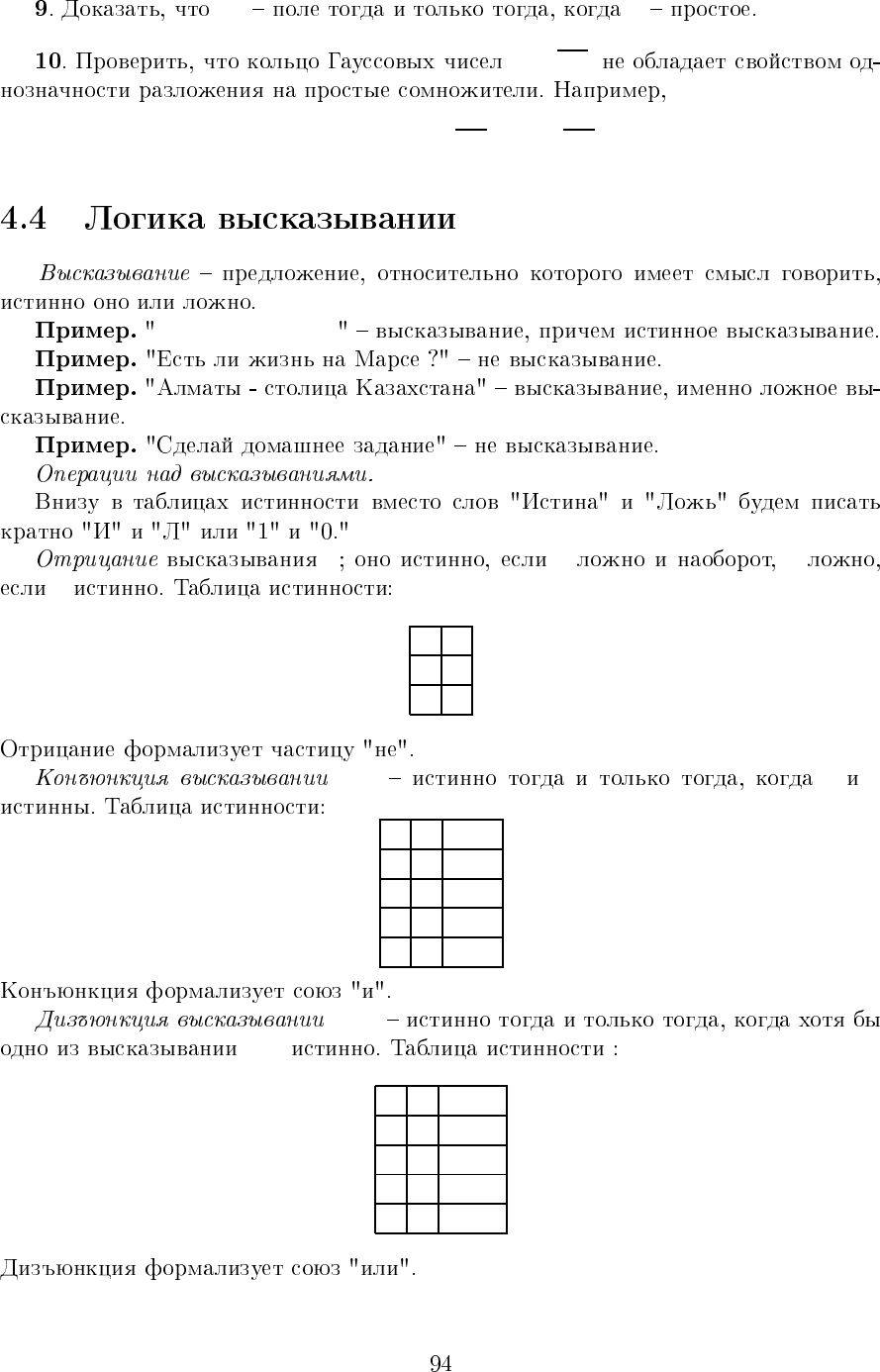
G = R\{0, −1}. f
i
: G → G, i =1, 2, 3, 4, 5, 6,
f
1
(x)=x, f
2
(x)=1− x, f
3
(x)=
1
x
,
f
4
(x)=
1
1 − x
,f
5
(x)=1−
1
x
,f
6
(x)=
x
x − 1
.
G
S
3
.
a
2
= e
Z
∗
n
= {i ∈ Z|0 <i<n, (i, n)=1}
Z
∗
30
.

12345
24153
1234567
7624153
12345
24153
12345
53421
Z[i]={a + bi|a, b ∈ Z}
Z[i]
{±1, ±i, ±j, ±k}, i
2
= j
2
= k
2
= −1,ij= k = −ji, jk = i = −kj, ki = j = −ik.
a, b
a
4
= e, b
2
= a
2
,bab
−1
= a
−1
.
G
01
−10
01
10
Q
D
n
n
01
10
η 0
0 η
−1
η = e
2πi
n
n
• (x
1
+ x
2
)(x
3
+ x
4
)
• (x
1
− x
2
)(x
3
−x
4
)
• (x
1
− x
2
)
2
+(x
2
− x
3
)
2
+(x
3
− x
4
)
2
+(x
4
− x
5
)
2
.
a, b
a
3
= b
2
= e, ab = ba
2
.
G Z(G)={a ∈ G|ab = ba, ∀b ∈ G}
Z(G) G.
S
4

• A
4
•
{
1234
1234
,
1234
2143
,
1234
3412
,
1234
4321
}
• K
•
+
• 0
• f : K → K
• ◦
(K, +, ◦, 0,f) K
• (K, +, 0,f)
• a ◦ (b + c)=a ◦ b + a ◦ c
• (a + b) ◦ c = a ◦ c + b ◦ c
f(a)
+ −a.
a ◦ (b ◦ c)=(a ◦ b) ◦ c, ∀a, b, c ∈ K,
a ◦ e = e ◦ a = a, ∀a ∈ K,
a ◦ b = b ◦ a, ∀a, b ∈ K,
(Z, +, ·, 0, 1)

(Mat
n
, +, ◦, 0, 1)
X ◦ Y 0 1
(K, +, ·, 0, 1)
K 0
1
∀a ∈ G ∃b ∈ G, a · b =1.
(Q, +, ·, 0, 1), (R, +, ·, 0, 1), (C, +, ·, 0, 1).
Z
2
= {0, 1}
Q[
√
2] = {a + b
√
2|a, b ∈ Q}
P (X) X. (P (X), ⊕, ∩)
⊕ ∩
⊕ ∩ X = {a, b, c}.
f : P (X) → Z
2
,f(∅)=
¯
0,f(X)=
¯
1,
|X| =1.
f : Z
24
→ Z
4
,f(x(mod 24)) = x(mod 4),
Z
2
× Z
3
∼
=
Z
6
(R, +, ·) ⊕ ◦ R
r ⊕ s = r + s +1,r◦ s = r ·s + r + s.
•
(R, ⊕, ◦)
• (R, ⊕, ◦).
•
(R, ⊕, ◦) (R, +, ·)
x
3
+2x
2
+ x +2 x
2
+2 Z
3
[x].
x
4
+ x
3
+3x −9 2x
3
−x
2
+
6x − 3
Q[x].
−
9
4
x
2
−
27
4
.
Z
n
n
Q[
√
−3]
4=2· 2=(1+
√
−3)(1 −
√
−3).
sin
2
x + cos
2
x =1
¯p p ¯p
p
p ¯p
0 1
1 0
p&q p q
p q p&q
1 1 1
1 0 0
0 1 0
0 0 0
p ∨q
p, q
p q p ∨ q
1 1 1
0 1 1
1 0 1
0 0 0

p → q
q p
p q p → q
1 1 1
0 1 1
1 0 0
0 0 1
p → q
• q → p p → q
• ¯p → ¯q
p → q
• ¯q → ¯r
p → q
p q
p
q
p → q
0 1.
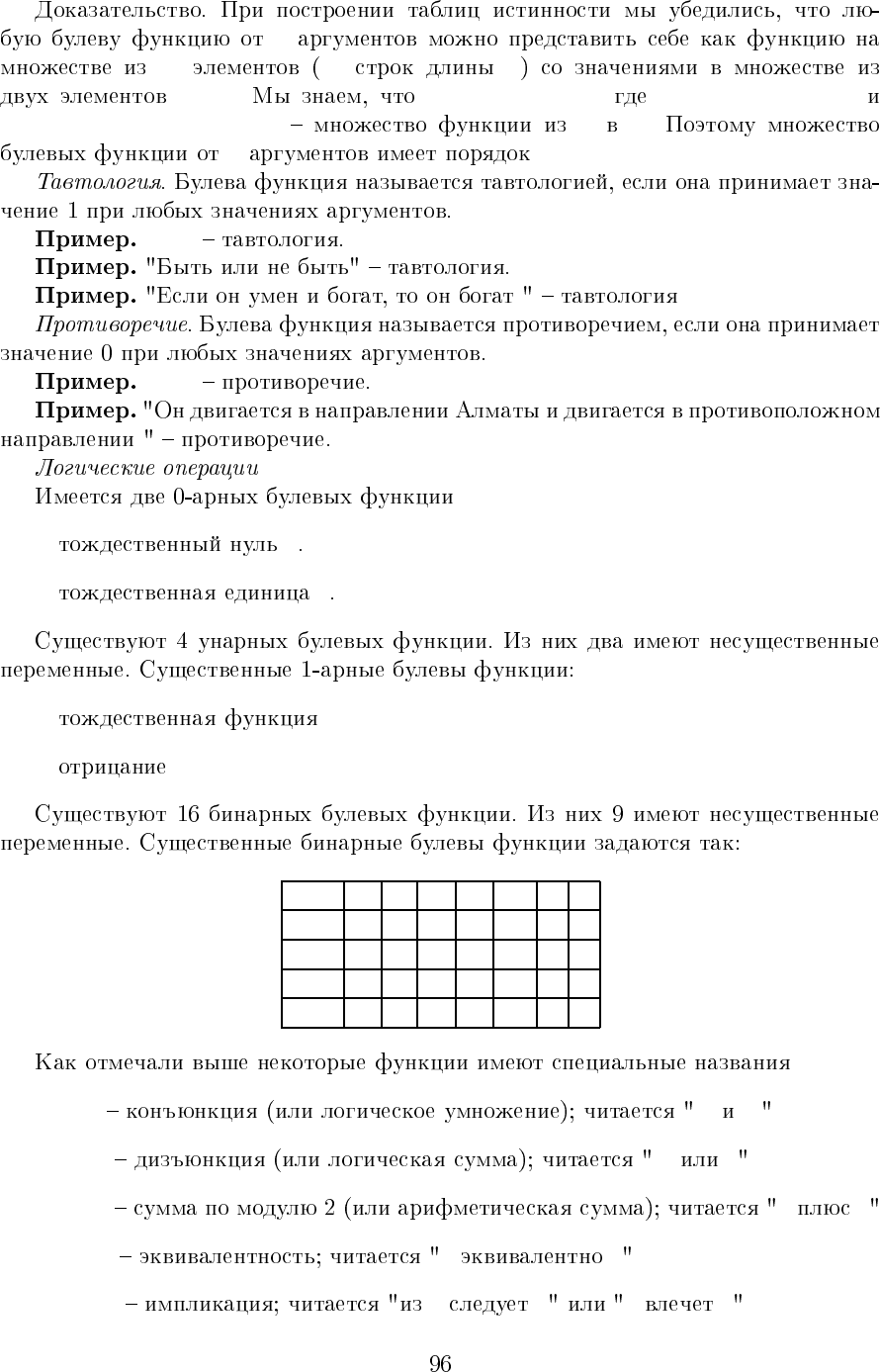
f(p
1
,...,p
k
) k
p
1
p
2
... p
k−1
p
k
f(p
1
,...,p
k
)
00··· 00f(0, 0,...,0, 0)
00··· 01f(0, 0,...,0, 1)
00··· 10f(0, 0,...,1, 0)
··· ··· ··· ··· ··· ···
11··· 11f(1, 1,...,1, 1)
0 1 2
k
f(p
1
,...,p
k
)
2
2
n
n
n
2
n
2
n
n
{0, 1}. |F(A, B)| = m
n
, |A| = n, |B| = m,
F(A, B)={f : A → B} A B.
n 2
2
n
.
p ∨ ¯p
p ∧ ¯p
• 0
• 1
• p
•
¯p
pq& ∨ ⊕ ≡ → ↑ ↓
00 0 0 0 1 1 1 1
01 0 1 1 0 1 1 0
10 0 1 1 0 0 1 0
11 1 1 0 1 1 0 0
• p&q p q
• p ∨ q p q
• p ⊕q p q
• p ≡ q p q
• p → q p q p q
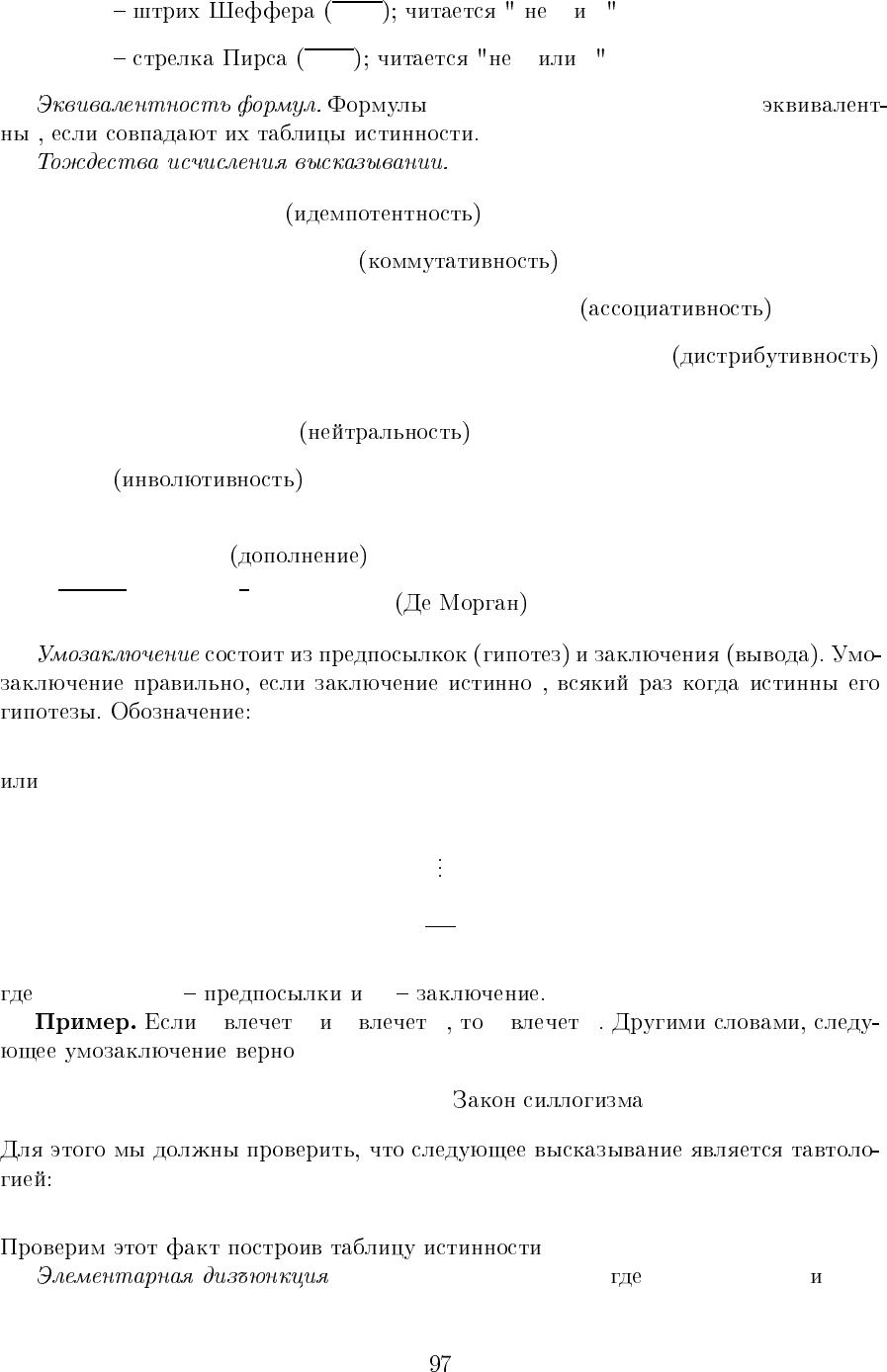
• p ↑ q p ∧ q p q
• p ↓ q p ∨ q p q
f(p
1
,p
2
,...,p
k
),g(p
1
,p
2
,...,p
k
)
• p ∨ p ≡ p, p ∧ p ≡ p
• p ∨ q ≡ q ∨ p, p ∧ q ≡ q ∧ p
• (p ∨ q) ∨ r ≡ p ∨ (q ∨ r), (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
• (p ∨q) ∧r ≡ (p ∧r) ∨(q ∧r), (p ∧q) ∨r ≡ (p ∨r) ∧(q ∨r)
• p ∨ F ≡ p, p ∧ F ≡ F,
p ∨ T ≡ T, p ∧ T ≡ p
•
¯
¯p ≡ p
• p ∨ ¯p ≡ T, p ∧ ¯p ≡ F
¯
T ≡ F,
¯
F ≡ T
• (p ∨ q) ≡ ¯p ∧ ¯q, (p ∧ q) ≡ ¯p ∨ ¯q
P
1
,P
2
, ···,P
k
Q
P
1
P
2
P
k
Q
P
1
,P
2
,...,P
k
Q
p q q r p r
p → q, q → r p → r .
(p → q) ∧(q → r) →)p → r)
x
δ
= x
δ
1
∨ x
δ
2
∨···∨x
δ
k
k
, δ
1
,...δ
k
=0, 1 x
1
i
=
x
i
,x
0
i
=¯x.

x
δ
= x
δ
1
∧ x
δ
2
∧···∧x
δ
k
k
, δ
1
,...δ
k
=0, 1 x
1
i
=
x
i
,x
0
i
=¯x.
(p ∧ ¯q) ∨ (p ∧ ¯q ∧ r)
(¯p ∨ q) ∧ (¯p ∨ ¯q) ∧ (¯p ∨ ¯r)
(p
1
,p
2
,...,p
n
)
p
i
(p
1
,p
2
,...,p
n
) p
i
¯p
i
.
(p
1
∧ ¯p
2
∧ p
3
) ∨ (¯p
1
∧ p
2
∧ p
3
)
(p
1
∧ ¯p
2
∧ p
3
) ∨ (¯p
1
∧ p
2
∧ p
3
) ∨ (p
1
¯p
2
∧p
3
)
(p
1
,p
2
,...,p
n
) p
i
(p
1
,p
2
,...,p
n
) p
i
¯p
i
.
(p
1
∨ p
2
∨ ¯p
3
) ∧ (¯p
1
∨ p
2
∨ p
3
) ∧ (p
1
∨ p
2
∨ ¯p
3
)
(p
1
∨ p
2
∨ ¯p
3
) ∧ (¯p
1
∨ p
2
∨ p
3
) ∧ (p
1
∨ p
2
)
f(p
1
,...,p
n
)
f(p
1
,...,p
k
,p
k+1
,...,p
n
)=∨
δ
&
k
i=1
p
δ
i
i
&f(δ
1
,...,δ
k
,p
k+1
,...,p
n
),
δ
i
=0, 1; i =1, 2,...,k,
p
δ
i
i
= {
p
i
δ
i
=1,
¯p
i
δ
i
=0
.
δ =(δ
1
,...,δ
k
).
n = k
f(p
1
,p
2
,...,p
n
)
f(p
1
,p
2
,...,p
n
)=∨
δ
&
k
i=1
p
δ
i
i
.
δ =(δ
1
,δ
2
,...,δ
n
),
f(δ
1
,δ
2
,...,δ
n
)=1.
f(p
1
,...,p
n
)
f(p
1
,...,p
k
,p
k+1
,...,p
n
)=∧
δ
(∨
k
i=1
p
¯
δ
i
i
∨ f(δ
1
,...,δ
k
,p
k+1
,...,p
n
)),

δ
i
=0, 1; i =1, 2,...,k,
p
δ
i
i
= {
p
i
δ
i
=1,
¯p
i
δ
i
=0
.
δ =(δ
1
,...,δ
k
).
n = k
f(p
1
,p
2
,...,p
n
)
f(p
1
,p
2
,...,p
k
)=∧
δ
(∨
k
i=1
p
¯
δ
i
i
).
δ =(δ
1
,δ
2
,...,δ
n
),
f(δ
1
,δ
2
,...,δ
n
)=0.
•
•
• p q,
• p
q,
• p,
q,
• p
q.
p q
• ¯p
• p ∧ q
• p ∨ q
• q ∨ ¯p
