Джумадильдаев А.С. Элементы дискретной математики (часть 1)

3S[a, b, c] S[d, e]+3S[b, c, d] S[e, a]+3S[c, d, e] S[a, b]

+3S[d, e, a] S[b, c]+3S[e, a, b] S[c, d]

−S[a, b, d] S[c, e] − S[b, c, e] S[d, a] − S[c, d, a] S[e, b]

−S[d, e, b] S[a, c] −S[e, a, c] S[b, d]

=10S[a, b, c, d, e],

S[a, b, c, d, e]=(a − b)(b − c)(c − d)(d − e)(e − a).

A F

k

(A, A)

k A ×···×A → A.

F

k

(A, A) ×F

l

(A, A) →F

k+l

(A, A)

ψφ(a

1

,...,a

k+l

)=



σ∈Sym

k,l−1

sgn σ ψ(a

σ(1)

,...,a

σ(k)

)φ(a

σ(k+1)

,...,a

σ(k+l−1)

,a

k+l

),

Sym

k,l

= {σ ∈ Sym

k+l

|σ(1) <...<σ(k),σ(k +1)< ···<σ(k + l)}.

s

k

(a

1

,...,a

k

)=(a

1

−a

2

)(a

2

−a

3

) ···(a

k−1

−a

k

)(a

k

− a

1

).

s

2i

s

l

=2



[l/2] + i − 1

i



s

2i+l

,

s

2i+1

s

l

=0, ∀0 <i,1 <l.

2k+1



i=1

(−1)

i

s

2k

(a

1

,..., ˆa

i

,...,a

2k+1

)=−2(a

1

− a

2

)(a

2

− a

3

) ···(a

2k

− a

2k+1

),

2k+1



i=1

(−1)

i

a

i

s

2k

(a

1

,..., ˆa

i

,...,a

2k+1

)=−(a

1

−a

2

)(a

2

− a

3

) ···(a

2k

− a

2k+1

)(a

2k+1

+ a

1

),

2k+1



i=1

(−1)

i

a

2

i

s

2k

(a

1

,..., ˆa

i

,...,a

2k+1

)=−2a

1

a

2k+1

(a

1

− a

2

) ···(a

2k

−a

2k+1

).

2k+1



i=1

(−1)

i

a

r

i

s

2k

(a

1

,..., ˆa

i

,...,a

2k+1

)

(a

1

− a

2

) ···(a

2k

− a

2k+1

)

r.

2k



i=1

(−1)

i

s

2k− 1

(a

1

,..., ˆa

i

,...,a

2k

)=0,

2k



i=1

(−1)

i

a

i

s

2k− 1

(a

1

,..., ˆa

i

,...,a

2k

)=0,

2k



i=1

(−1)

i

a

2

i

s

2k− 1

(a

1

,..., ˆa

i

,...,a

2k+1

)=0,

2k



i=1

(−1)

i

a

3

i

s

2k− 1

(a

1

,..., ˆa

i

,...,a

2k+1

)=(

2k− 1



i=1

(−1)

i

a

i

a

i+1

+ a

2k

a

1

)s

2k

(a

1

,...,a

2k

).

2k



i=1

(−1)

i

a

r

i

s

2k− 1

(a

1

,..., ˆa

i

,...,a

2k

)

s

2k

(a

1

,...,a

2k

)

r.

4



i=1

(−1)

i

a

3

i

s

3

(a

1

,..., ˆa

i

,...,a

4

)=



1≤i<j≤4

(a

i

−a

j

),

4



i=1

(−1)

i

a

4

i

s

3

(a

1

,..., ˆa

i

,...,a

4

)=(

4



i=1

a

i

)



1≤i<j≤4

(a

i

−a

j

),

4



i=1

(−1)

i

a

5

i

s

3

(a

1

,..., ˆa

i

,...,a

4

)=(



1≤i<j≤4

a

i

a

j

)



1≤i<j≤4

(a

i

−a

j

).

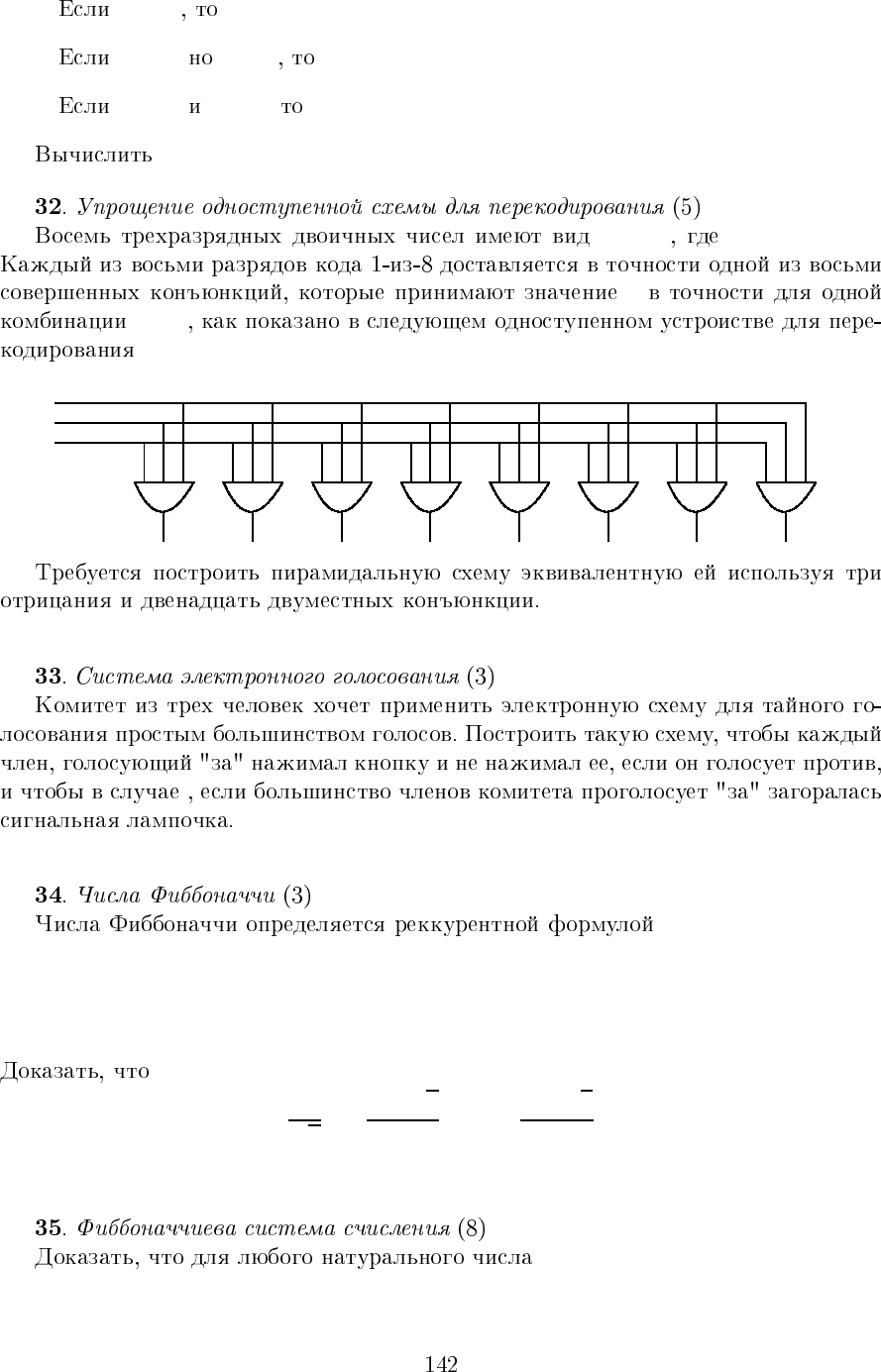
• m =0 A(m, n)=n +1.

•

m =0 n =0 A(m, n)=A(m − 1, 1)

•

m =0 n =0, A(m, n)=A(m − 1,A(m, n − 1)).

A(1, 3).

(a, b, c) a, b, c ∈{0, 1}.

1

a, b, c

a

b

c

r

rrrrrrrrrrrr

F

0

=0,F

1

=1,

F

n

= F

n−1

+ F

n−2

,n>1.

F

n

=

1

√

5



1+

√

5

2



n

−



1 −

√

5

2



n



.

a ∈ N

•

a = λ

1

F

n

+λ

2

F

n−1

+···+λ

n−1

F

2

λ

1

,λ

2

,...,λ

n−1

0, 1 λ

i

λ

i+1

=0, i ≥ 1.

•

λ

1

,λ

2

,...,λ

n−1

a λ(a)=λ

1

λ

1

···λ

n−1

a λ(19) = 101001

19 = F

7

+ F

5

+ F

2

.

•

N,

f

N

f

3

0

1

,

1

3

,

1

2

,

2

3

,

1

.

•

f

N

N>1

•

a

b

c

d

f

N

. ad − bc =1.

•

1

b

c

d

a+c

b+d

a+b

c+d

• f

N



N

i=1

φ(i)+ 1.

•

a

b

≤ α ≤

c

d

,

a

b

c

d

f

N

.

|α −

a

b

| <

1

√

5b

2

, |α −

c

d

| <

1

√

5d

2

, |α −

a + c

b + d

| <

1

√

5(b + d)

2

.

p

∂ =

∂

∂x

C[x].

f = f(x) ∈ C[x]

∂

p−2

(f

p−1

)+(f∂)

p−2

(f) ≡ 0(mod p).

p. p =3.

∂(f

2

)=2f∂(f) ⇒ ∂(f

2

)+f∂(f )=3f∂(f) ≡ 0(mod3)

p =5.

∂

3

(f

4

)=∂

2

(4f

3

∂(f)) = ∂(12f

2

(∂(f))

2

+4f

3

∂

2

(f))

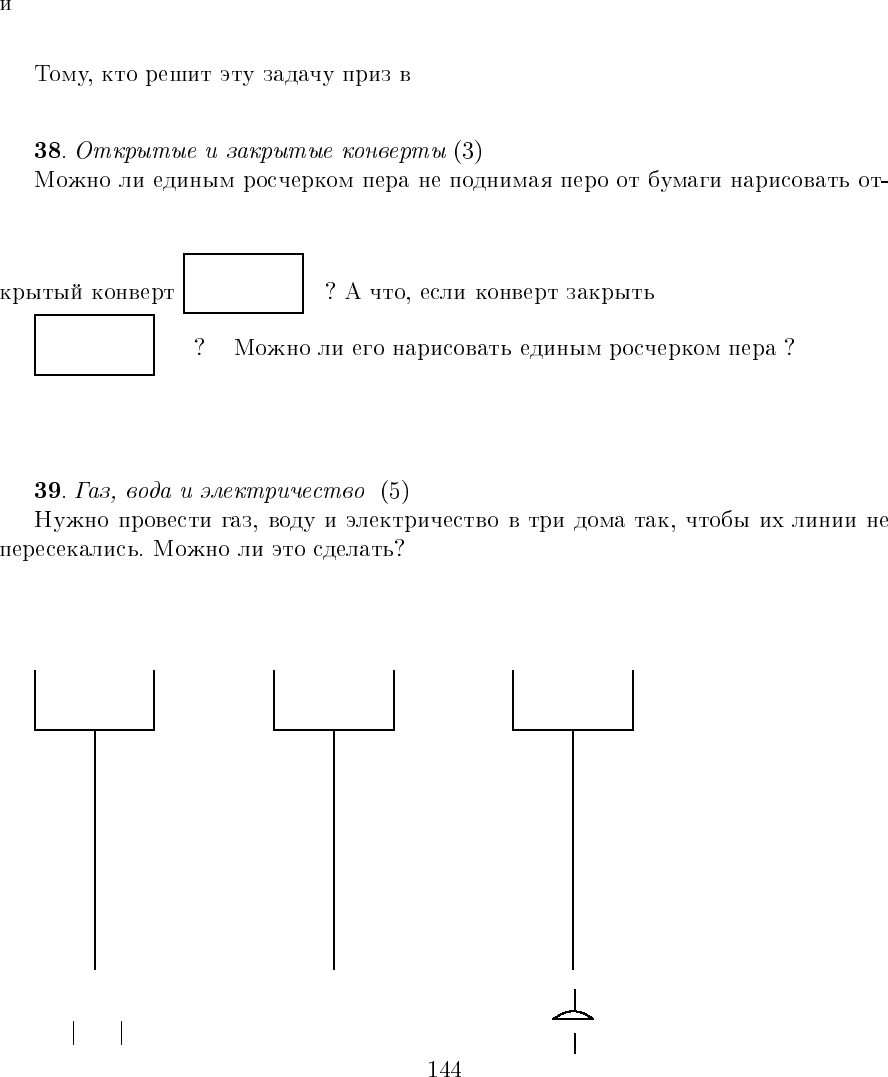
=24f(∂(f ))

3

+24f

2

∂(f)∂

2

(f)+12f

2

∂(f)∂

2

(f)+4f

3

∂

3

(f)

=24f(∂(f ))

3

+36f

2

∂(f)∂

2

(f)+4f

3

∂

3

(f)

(f∂)

3

(f)=(f∂)

2

(f∂(f )) = f∂(f

2

∂

2

(f)+f(∂(f))

2

)=2f

2

∂(f)∂

2

(f)+f

3

∂

3

(f)

+f(∂(f ))

3

+2f

2

∂(f)∂

2

(f)

= f(∂(f ))

3

+4f

2

∂(f)∂

2

(f)+f

3

∂

3

(f)

∂

3

(f

4

)+(f∂)

3

(f)=25f(∂(f))

3

+40f

2

∂(f)∂

2

(f)+5f

3

∂

3

(f) ≡ 0(mod5).

300$



H



@

H





@





@





@



@

H



@





&%

'$

&%

'$

&%

'$



(((((((

===

)





%



 Q

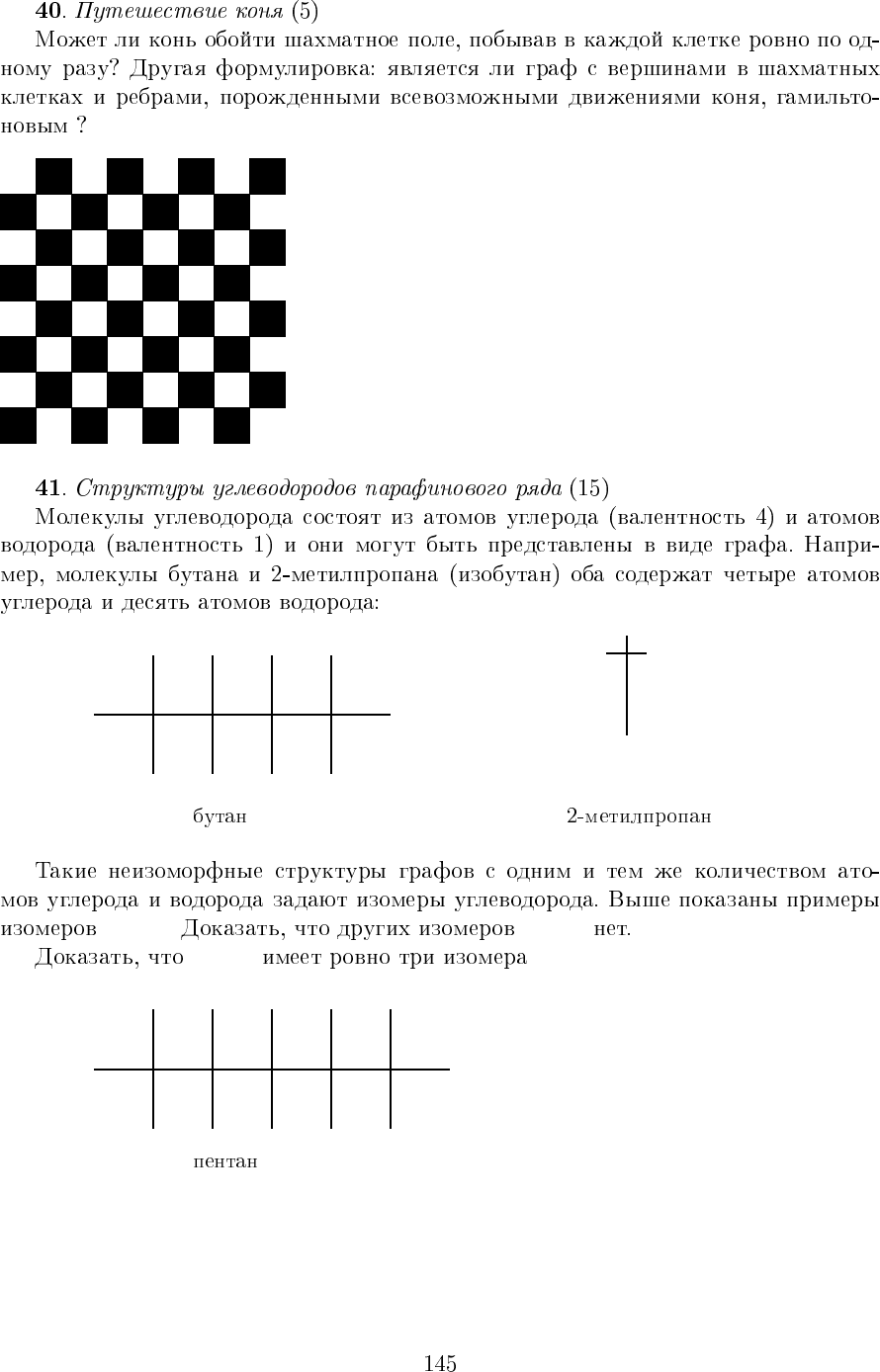
rrrrrr

rrrr

r

rr

rr rr

rr



@

@



C

4

H

10

. C

4

H

10

C

5

H

12

rrrrrr

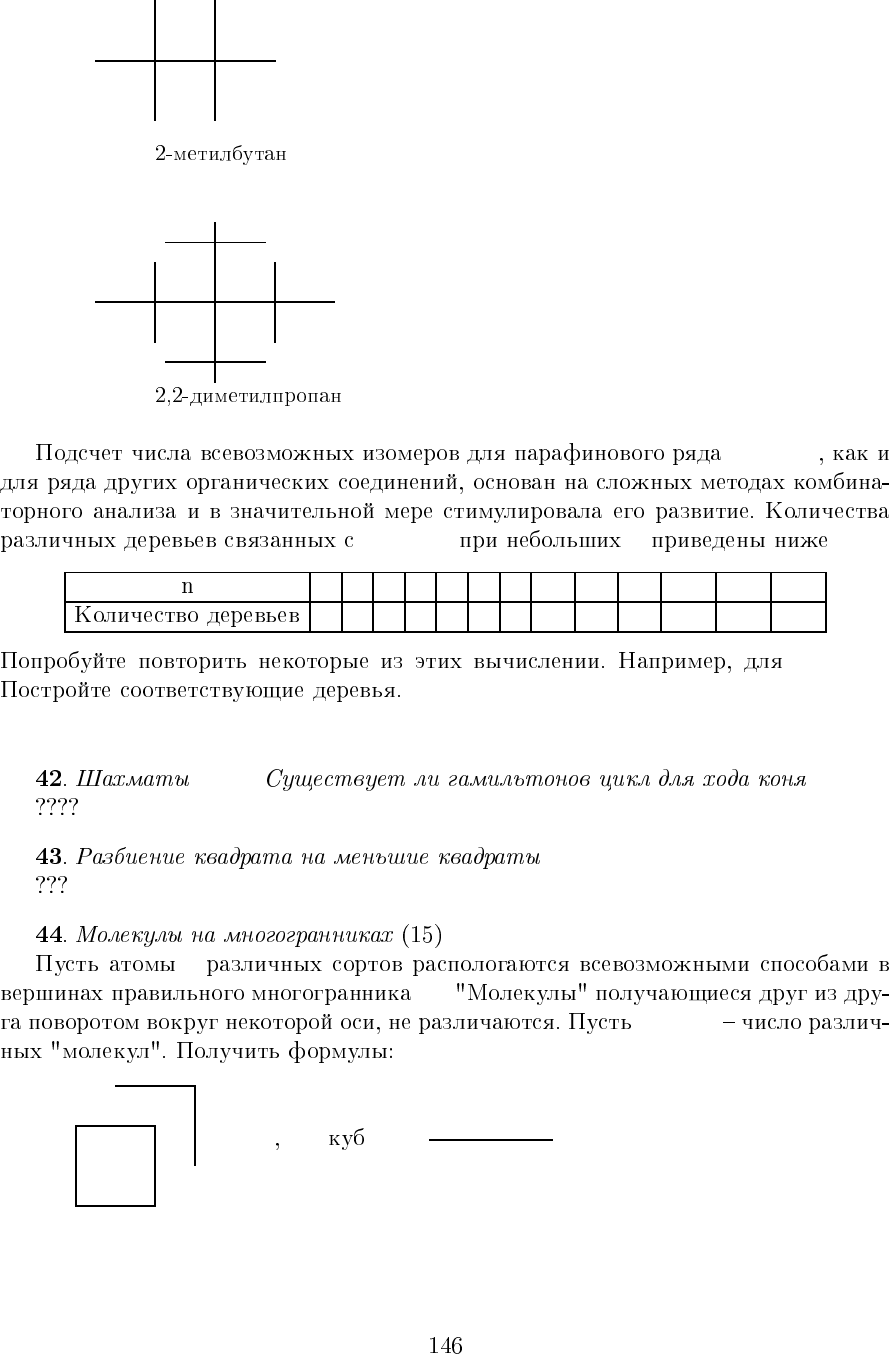
rrrr

r

rrrr

rr

r

@



rr

r

r@

@



rrrrr

r

rr

C

n

H

2n+2

C

n

H

2n+2

n

1 2 3 4 5 6 7 8 9 10 11 12 13

1 1 1 2 3 5 9 18 35 75 159 357 799

n =6, 7.

5 × 5.

q

M.

f(M,q)

M =

rr

p

pppppppppp

p



f( ,q)=

q

2

(q

6

+17q

2

+16)

24

,

M =

H



@

@



rr

r

pppppppppppppppp

,f( ,q)=

q

2

(q

2

+11)

12

,

M =

r

X



p

pp

p



Z

Z



@

%

B

p

,f( ,q)=

q

2

(q

4

+3q

2

+12q+8)

24

CH

3

H



@

@



CH

3

H OH

Br



@

@



Br



@

@



Br



@

@



Br



@

@



Br



@

@



Br



@

@



Br

Br Br



@

@



Br



@

@



Br

Br Br



@

@



Br



@

@



G G M

α : G × M → M

α(g ◦h, m)=α(g, α(h, m)), ∀g, h ∈ G, ∀m ∈ M,

α(e, m)=m, ∀m ∈ M.

α(g, m) g(m).

Fixg = {m ∈ M|gm = m}

g ∈ G. M

mRn m = g(n) g ∈ G. R

N =

1

|G|



g∈G

|Fixg|.

Джумадильдаев А.С. Элементы дискретной математики (часть 1)

Подождите немного. Документ загружается.