Джумадильдаев А.С. Элементы дискретной математики (часть 1)
Подождите немного. Документ загружается.


p q
r
•
•
•
¯p ∧ q
p ∨ p ∧ q
p ∧ q ¯p ∨ ¯q
•
•
•
•
•
• p → q, ¯p ¯q
• p → q, ¯q ¯p
• p → ¯q, r → q, r → ¯p
•
•

(((p ∧ q) → r) ∧ (p → q)) → (p → r)
((p ∧ q) → r) → (p → (q → r))
• p → q, q → r p → r
• p → (q → r) q → (p → r)
• p → (q → r) (p ∧q) → r
• p → q (p ∧ r) → (q ∧ r)
• p → q (p ∨ r) → (q ∨ r)
• ¯p p → r
• (p ∨ q) → (p ∧ q)
• ((p → q) → q) → p
• ((p → q) → q) → q
•
p ∨ ¯p → (p ∨ ¯p)
• p →
p → ¯p
• (p → q) → (q → p)
M
n
(r) r
M
n
(r)=
n
r
n−r
k=0
(−1)
k
n − r
k
2
2
n−r−k
,r=0, 1,...,n− 1.
A
i
f(x
1
,...,x
n
)
x
i
. A
i
1
∩···A
i
k
2
n−k
|A
i
1
∩···∩A
i
k
| =2
2
n−k
.
r
n
r

A
(a, b) → a + b, (a, b) → a · b,
a → ¯a 0, 1.
x + y = y + x, x · y = y · x
x +(y + z)=(x + y)+z, x · (y · z)=(x · y) · z
x · (x + y)=x, x +(x · y)=x
x +(y · z)=(x + y) · (x + z),x· (y + z)=x · y + x · z
x · 0=0,x+0=x, x · 1=x, x +1=1
x · ¯x =0,x+¯x =1
A
x + x = x, x ·x = x
y = x · x
x(x + x · x)=x,
x + x · x = x.
x · x = x.
x + x = x
x · y =¯x +¯y, x + y =¯x · ¯y
¯x = x
· ¯a
·
P (A) A P (A)
∨, ∧ 0
∅ 1 A (P (A), ∨, ∧,¯, 0, 1)
D(n) n.

N
a ≺ b ⇔ a|b.
D
m
m D
m
a + b = a ∨ b = (a, b),a b = a ∧ b = (a, b)
≺, ! "
2 8; 18 24; 9 3; 5 15.
N {24, 2, 6};
{3, 15, 5}; N; {2, 8, 32, 4}; {7}; {15, 5, 30}
A = {1, 2, 3, 4, 5}
@
@
@
@
4
2
5
1
3
•
≺, ! " 15; 23;
41; 34
•
A. A
• L(A)
A
L(A).
D
m
m D
m
a + b = (a, b),ab= (a, b),
m D
m
.
p∧q
p q.
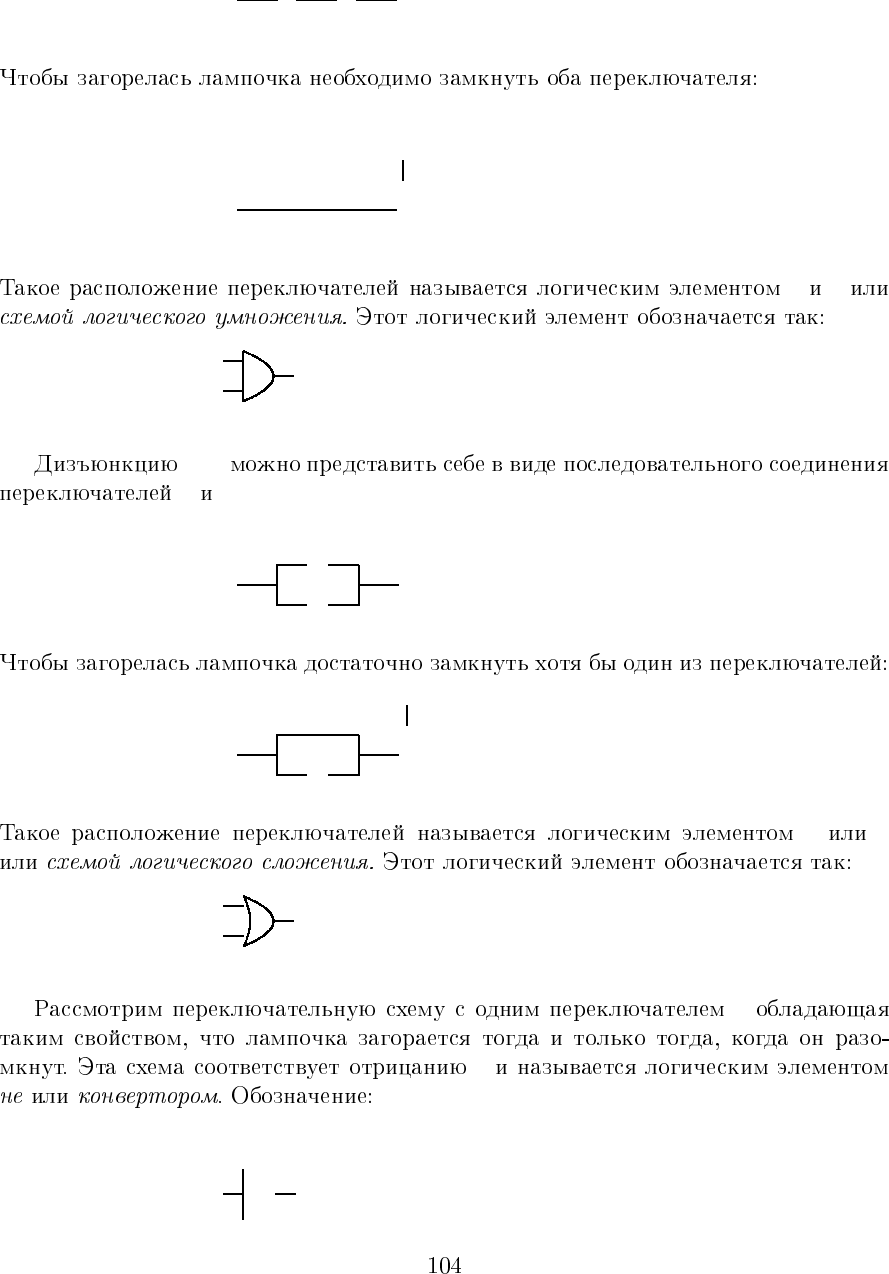
=|⊃
xy
=|⊃
xy
@
p q
-
-
-
p∧q
p q.
=|⊃
x
y
=|⊃
@
x
y
p q
-
-
-
p
¯p
@
@
c
--

p ∧ q ∧ ¯r
@
@
c
--
-
-
-
-
p
q
r
p ∧ q ∧ ¯r
x
y
-
-
-
x ∧ y
x
y
-
x ∨ y
-
-
x
@
@
c
-
¯x
-
pqr + p¯q¯r +¯pq¯r +¯p¯qr

G V = V (G)
E = E(G) E ⊆ V × V. e =(u, v) u v
e.
u v u v e
e u v e = uv.
e =
−→
uv
r
r
u v e.
v
0
e
0
v
1
e
1
...v
s−1
e
s−1
v
s
e
i
=(v
i−1
,v
i
) v
i−1
v
i
.
v
0
e
0
v
1
e
1
...v
s−1
e
s−1
v
s
v
0
v
1
...v
s−1
v
s
.
(a
i,j
) n×m, n = |V | m = |E|.
V
E.
a
i,j
=
1
v
i
e
j
0
(b
i,j
) n × n, n = |V |.
V.
b
i,j
=
s
v
i
v
j
s
0

G
b
i,j
=
1???
v
i
v
j
0
G =(V,E) W =(w
i,j
)
w
i,j
=
1,
v
i
v
j
0,
1+1 = 1 1+1 = 0
W
∗
W
1
= W
W
1
W
2
.
W
2
W
2
W
3
n W
n
.
W
∗
G.
W
∗
n
W
i
= W
i+1
= ···. W
∗
= W
i
.
W
∗
W
∗
=(w
∗
i,j
) w
∗
i,j
=1,
v
i
v
j
. w
∗
i,j
=0,
-
6 6@
@
@
@R
-
W =
01010
00100
10001
00100
00000
W
0
= W =
01010
00100
10001
00100
00000

W
1
=
01010
00100
11011
00100
00000
W
2
=
01110
00100
11111
00100
00000
W
3
=
11111
11111
11111
11111
00000
W
i
= W
3
,
i>3.
W
∗
= W
3
=
11111
11111
11111
11111
00000
•
•
•

•
•
G =(V, E) ν(G)=|E|−|V | +1
G =(V,E) |V |−1
ν(G)
r
r
rr
r
12
A
B
C
D
e =7 v =4
1, 2, 3; 3, 6, 7; 1, 2, 4, 6, 7.
r
r
rr
r
12
A
B
C
D
pppppppp`
`
`
`
`
`
p
p
p
p
p
p
pppppppp
pppppppppppppppppppppppp
•
±i
k
=0.
