Джумадильдаев А.С. Элементы дискретной математики (часть 1)
Подождите немного. Документ загружается.


A
a, b ∈ A A,
ab a b.
A × A → A, (a, b) → ab.
a
1
,a
2
,...,a
k
α
n
n
α
1
=1.
α
2
=1,α
3
=2,α
4
=5.
n =2, (a
1
a
2
),
n =3, (a
1
a
2
)a
3
,a
1
(a
2
a
3
),
n =4, ((a
1
a
2
)a
3
)a
4
, (a
1
(a
2
a
3
))a
4
, (a
1
a
2
)(a
3
a
4
),a
1
((a
2
a
3
)a
4
),a
1
(a
2
(a
3
a
4
)).
α
n+1
=
1
n +1
2n
n
,n≥ 0.
α
k
k =1, 2,...,n− 1.
{a
1
,...,a
k
} α
k
{a
k+1
,...,a
n
} α
n−k
α
k
α
n−k
k
1, 2,...,n− 1,
α
n
=
n−1
i=1
α
i
α
n−i
,n>1.
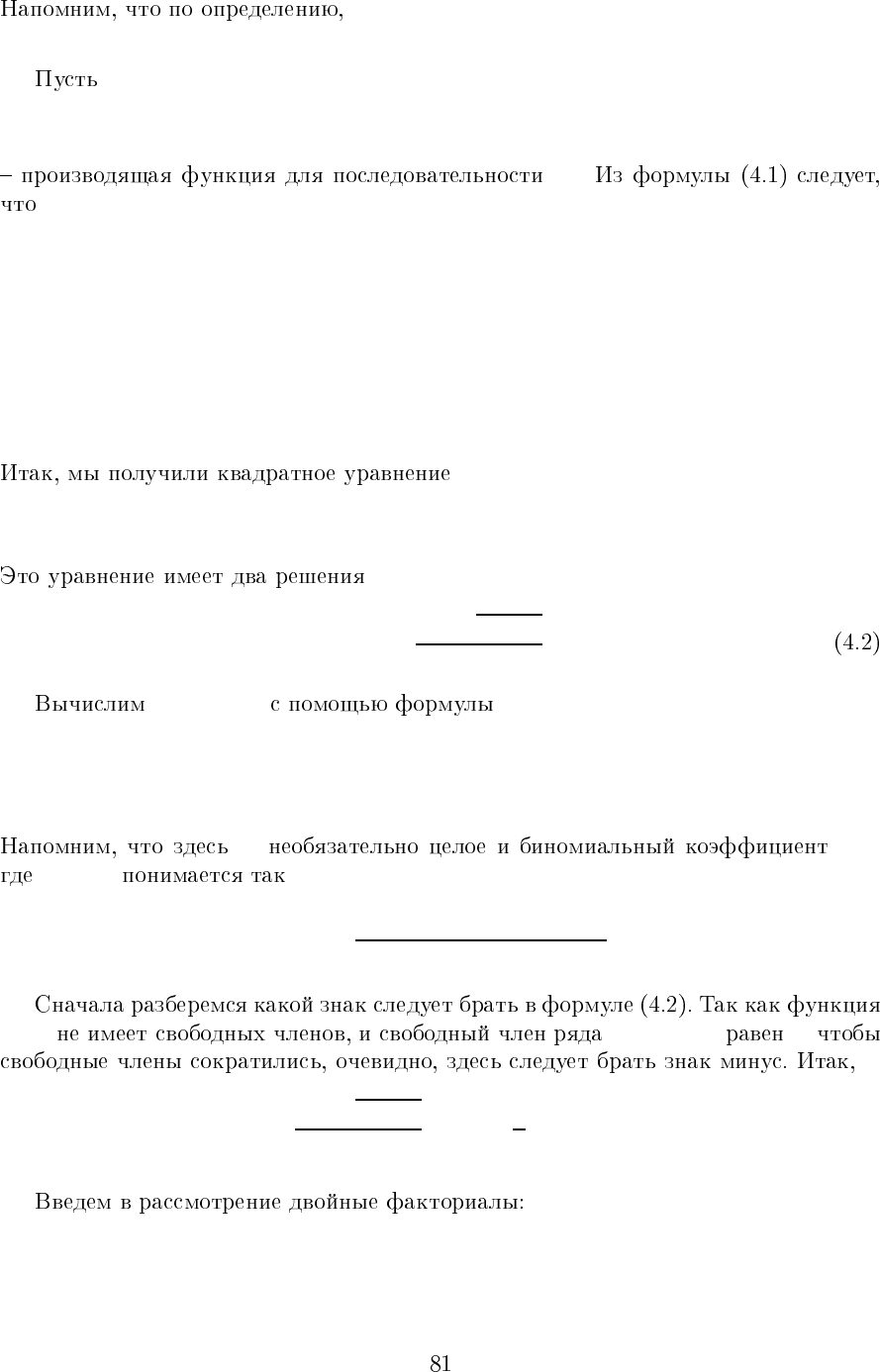
α
1
=1.
G(α)=
i≥1
α
i
x
i
α
n
.
G(α)G(α)=
(
i≥1
α
i
x
i
)(
j≥1
α
j
x
j
)=
i,j≥1
α
i
α
j
x
i+j
=
n≥2
(
n−1
i=1
α
i
α
n−i
)x
n
=
n≥2
α
n
x
n
=
n≥1
α
n
x
n
− α
1
x =
G(α) − x.
G(α)
2
− G(α)+x =0.
G(α)=
1 ±
√
1 − 4x
2
.
(1 − 4x)
1/2
(1 + t)
m
=
i≥1
m
i
t
i
.
m
m
i
,
i ∈ Z
+
,
m
i
=
m(m − 1) ···(m − i +1)
i!
.
G(x) (1 −4x)
1/2
1,
G(α)=
1 −
√
1 − 4x
2
=
i≥1
−
1
2
1/2
i
(−4x)
i
.
(2i − 1)!! = 1 · 3 · 5 ···(2i − 1)
(2i)!! = 2 · 4 ···(2i)

2i −1
2 2i.
(−1)
i+1
1/2
i
4
i
2
=(−1)
i+1
1/2(1/2 − 1) ···(1/2 − i +1))
i!
4
i
2
=
(−1)
i+1
1 · (1 − 2)(1 − 4) ···(1 − 2(i − 1))
2
i
4
i
2 · i!
=
1 · 3 ···(2i − 3)2
i−1
i!
=
1 · 3 ···(2i − 3)2
i−1
(i − 1)!
(i − 1)!i!
=
(2i − 1)!!(2(i − 1))!!
(i − 1)!i!
=
1
i
2(i − 1)
i − 1
.
G(α)=
n≥1
1
n
2(n − 1)
n − 1
x
n
.
α
n
=
1
n
2(n − 1)
n − 1
,n≥ 1,
• G
•
◦
• e

• f : G → G, a → f(a)
G
G
(G, ◦,e,f) G
a ◦ (b ◦ c)=(a ◦ b) ◦ c, ∀a, b, c ∈ G
a ◦ e = e ◦ a = a, ∀a ∈ G
a ◦ f(a)=e, ∀a ∈ A.
∀a ∈ G ∃b ∈ G, a ◦ b = e.
f(a) a
−1
−a.
a ◦ b = b ◦ a a, b ∈ G.
G = Z,a◦ b = a + b, e =0. (Z, +, 0) Z
Z a · b (Z, ·, 1)
GL
n
= {X ∈ Mat
n
|det X =0}
E =(δ
i,j
)
X F(X, X)
X. id ∈F(X, X)
id(x)=x, ∀x ∈ X.
f · g
f · g(x)=f(g(x)),f,g∈F(X, X).
A = F(X, X)
•
• e = id
•
1 n.
G = S
n
a ◦ b
e =
12··· n
12··· n

H ⊆ G G,
a ◦ b ∈ H a, b ∈ H. H ≤ G.
H ≤ G a ◦ h ◦ a
−1
inH
a ∈ G h ∈ H. H G.
G F ◦ α : G → F
α(a ◦ b)=α(a) α(b), ∀a, b ∈ G.
Ker α = {a ∈ G|α(a)=e}.
e F.
G H α : G → F
Ker α G.
a, b ∈ Ker α ⇒ α(a)=e, α(b)=e ⇒
α(a ◦ b)=α(a) α(b)=ee= e ⇒ a ◦ b ∈ KerG.
Ker α G.
a ∈ Ker α,b ∈ G ⇒ α(a)=e ⇒ α(b ◦ a ◦ b
−1
)=α(b) α(a) α(b)
−1
=
α(b) eα(b)
−1
= α(b) α(b)
−1
= e ⇒ b ◦ a ◦ b
−1
∈ KerG.
Ker α G.
G n G → S
n
.
a ∈ G L
a
: G → G
L
a
(b)=a ◦ b.
L
a◦b
(c)=(a ◦ b) ◦ c = a ◦ (b ◦ c)=a ◦ L
b
(c)=L
a
(L
b
(c)).
L
a◦b
= L
a
· L
b
,
·
L
a
= id ⇒ L
a
(b)=b, ∀b ∈ G ⇒ a ◦b = b ⇒ a = e.
G →F(G, G),a→ L
a
G F(G, G).

a ∈ G m a
m
= e, a
m−1
= e.
(a ◦ b)
−1
= b
−1
◦ a
−1
.
(a ◦ b) ◦ (b
−1
◦ a
−1
)=(a ◦ (b ◦ b
−1
)) ◦a
−1
=(a ◦e) ◦ a
−1
= a ◦ a
−1
= e.
H ≤ G
G a ◦ H = {a ◦ h|h ∈ H}
H ≤ G
G H ◦a = {h ◦ a |h ∈ h}.
H G
S
3
=
e =
123
123
,a
1
=
123
132
,a
2
=
123
321
,
a
3
=
123
213
,a
4
=
123
231
,a
5
=
123
312
S
3
H = {e, a
1
}.
e ◦ H = {e, a
1
} H ◦e = {e, a
1
}
a
2
◦ H = {a
2
,a
5
} H ◦ a
2
= {a
2
,a
4
}
a
3
◦ H = {a
3
,a
4
} H ◦ a
3
= {a
3
,a
5
}
H
S
3
.
S
4
H =
e =
1234
1234
,b
1
=
1234
2143
,b
2
=
1234
3412
,b
3
=
1234
4321
.
H
H S
4
.
G H ≤ G
|H| |G|.
R G aRb, a ◦
b
−1
∈ H. R
aRa, a ◦ a
−1
= e ∈ H

aRb ⇒ a ◦ b
−1
∈ H ⇒ (a ◦ b
−1
)
−1
∈ H ⇒ b ◦ a
−1
∈ H ⇒ bRa
aRb, bRc ⇒ a ◦ b
−1
∈ H, b ◦ c
−1
∈ H ⇒ a ◦ c
−1
=(a ◦ b
−1
) ◦ (b ◦ c
−1
) ∈ H ⇒ aRc
H ◦ g
1
,...,H ◦
g
k
G
G = ∪
k
i=1
H ◦ g
i
.
|H ◦g| = |H|,
g ∈ G.
h ◦ g = h
1
◦g, h, h
1
∈ H ⇒ h =(h
1
◦ g) ◦ g
−1
= h
1
.
|G| =
k
i=1
|H ◦ g
i
| = |H|k,
|G|/|H|∈Z.
p, p
a ∈ G e.
a
p a = e, a
p G
G
d
G, G d.
A
4
1, 2, 3. h
1
,h
2
,h
3
1, 2, 3.
J
J
J
J
J"
"
"
"
"
b
b
b
b
b
A
1
A
3
A
2
h
1
h
3
h
2

φ
1
= ,
φ
2
= 2π/3
φ
3
= 4/pi/3,
θ
1
= h
1
,
θ
2
= h
2
,
θ
3
= h
3
.
G
G
φ
2
◦ θ
1
= θ
2
.
φ
2
◦ θ
1
(A
1
)=φ
2
(θ
1
(A
1
)) = φ
2
(A
1
)=A
3
,
φ
2
◦ θ
1
(A
2
)=φ
2
(θ
1
(A
2
)) = φ
2
(A
3
)=A
2
,
φ
2
◦ θ
1
(A
3
)=φ
2
(θ
1
(A
3
)) = φ
2
(A
2
)=A
1
,
θ
2
(A
1
)=A
3
,
θ
2
(A
2
)=A
2
,
θ
2
(A
3
)=A
1
,
φ
2
◦θ
1
= θ
2
.
G.
G e = φ
1
◦ φ
1
φ
2
φ
3
θ
1
θ
2
θ
3
φ
1
φ
1
φ
2
φ
3
θ
1
θ
2
θ
3
φ
2
φ
2
φ
3
φ
1
θ
2
θ
3
θ
1
φ
3
φ
3
φ
1
φ
2
θ
3
θ
1
θ
2
θ
1
θ
1
θ
3
θ
2
φ
1
φ
3
φ
2
θ
2
θ
2
θ
1
θ
3
φ
2
φ
1
φ
3
θ
3
θ
3
θ
2
θ
1
φ
3
φ
2
φ
1

n
D
n
. D
n
2n
a, b
a
n
= e, b
2
= e, bab = a
n−1
.
n =4.
A
1
A
2
A
3
A
4
a
1
0
a
2
π/2
a
3
π
a
4
3π/2
b
1
B
1
B
3
b
2
A
2
A
4
b
3
B
2
B
4
b
4
A
3
A
1
@
@
@
@
@
@
A
1
A
2
A
3
A
4
B
1
B
2
B
3
B
4
a = a
1
,b = b
1
.
a
3
= a
3
.
a
4
= e, b
2
= e, b ◦ a ◦ b = a
3
.
(b ◦ a ◦ b)(A
1
)=(b ◦ a)(b(A
1
)) = (b ◦ a)(A
2
)) = b(a(A
2
)) = b(A
1
)=A
2
,
(b ◦ a ◦ b)(A
2
)=(b ◦ a)(b(A
2
)) = (b ◦ a)(A
1
)) = b(a(A
1
)) = b(A
4
)=A
3
,
(b ◦ a ◦ b)(A
3
)=(b ◦ a)(b(A
3
)) = (b ◦ a)(A
4
)) = b(a(A
4
)) = b(A
3
)=A
4
,
(b ◦ a ◦ b)(A
4
)=(b ◦ a)(b(A
4
)) = (b ◦ a)(A
3
)) = b(a(A
3
)) = b(A
2
)=A
1
.
a
3
−π/2
a
3
(A
1
)=A
2
,a
3
(A
2
)=A
3
,a
3
(A
3
)=A
4
,a
3
(A
4
)=A
1
.
b ◦ a ◦ b = a
3
.
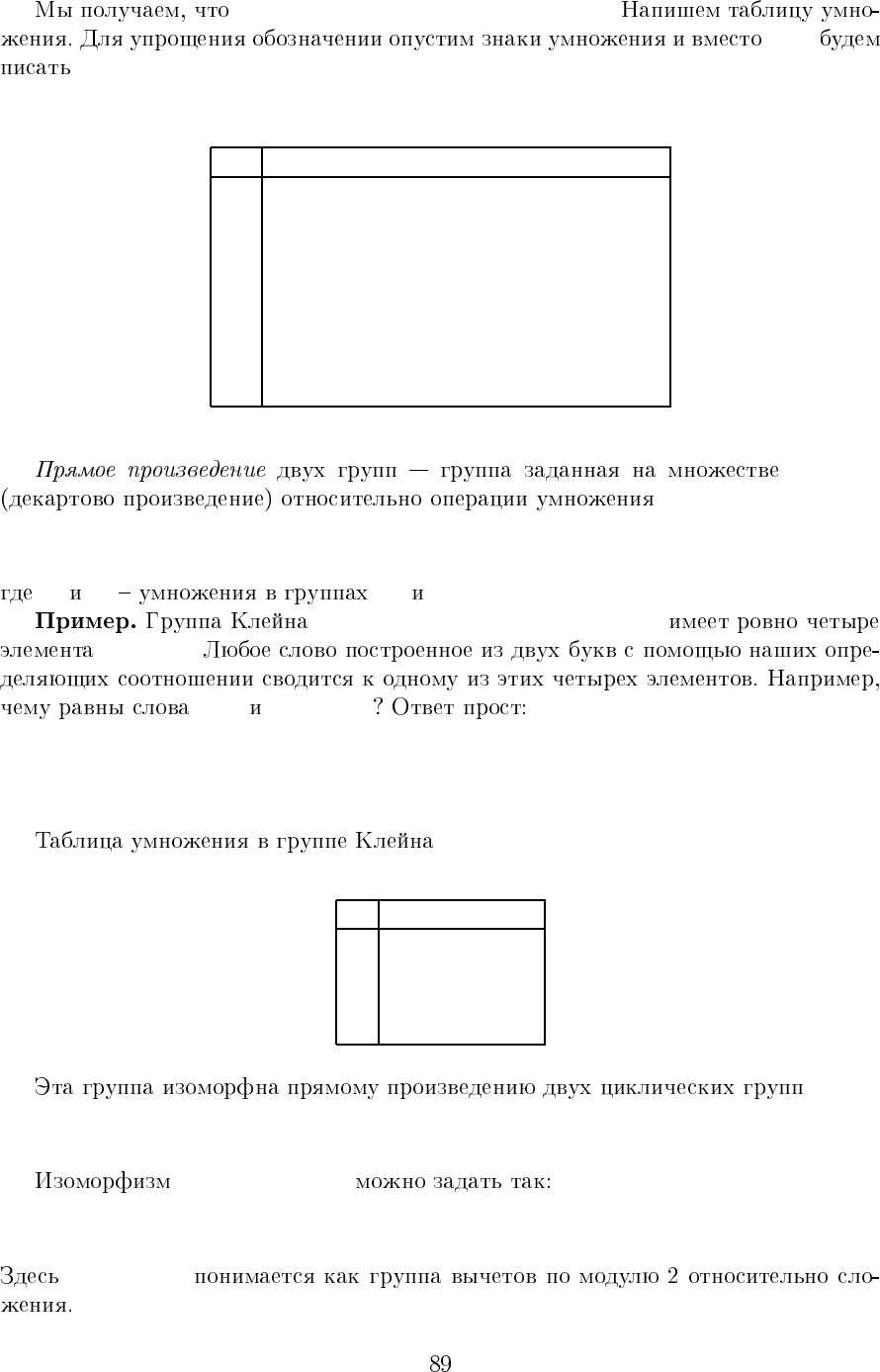
G = {e, a, a
2
,a
3
,b,a◦b, a
2
◦b, a
3
◦b}.
a
i
◦b
a
i
b.
eaa
2
a
3
baba
2
ba
3
b
e eaa
2
a
3
baba
2
ba
3
b
a aa
2
a
3
eaba
2
ba
3
bb
a
2
a
2
a
3
eaa
2
ba
3
bb ab
a
3
a
3
eaa
2
a
3
bb aba
2
b
b ba
3
ba
2
bab e a
3
a
2
a
ab ab b a
3
ba
2
ba e a
3
a
2
a
2
b a
2
bab b a
3
ba
2
aea
3
a
3
b a
3
ba
2
bab b a
3
a
2
ae
G
1
× G
2
(a
1
,a
2
) ◦ (b
1
,b
2
)=(a
1
◦
1
b
1
,a
2
◦
2
b
2
),
◦
1
◦
2
G
1
G
2
.
G = {a, b |a
2
= e, b
2
= e, ab = ba}
e, a, b, ab.
abba bababbaa
abba = aea = a
2
= e,
bababbaa = babaee = baba = baab = beb = bb = e.
eabab
e eabab
a aeabb
b babe a
ab ab b a e
G
∼
=
Z
2
× Z
2
.
f : G → Z
2
×Z
2
f(e)=(0, 0),f(a)=(0, 1),f(b)=(1, 0),f(ab)=(1, 1).
Z
2
= {0, 1}
