Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

5.2. Алгоритмы

скольжения

2-го порядка 201

Пусть

Ti —

время

i-ro

оборота. Очевидно,

что

т;-= г'+ г

•

г^

+ г^

где

для

промежутков

rj (j = 1,2,3,4)

нетрудно получить выражения

.•

к2(<'о)|

.•

к2(4)1

г;

к2(4)1

п =

Ал

+ *2

к2(П)|

^ ki-k2'

•'

ki-k2

Используя последние соотношения, нетрудно убедиться,

что

верна сле-

дующая оценка:

ki-k2

(k2(4)|

2|<T2(4)l+k2(<i)|)

ifcj

jt2

(^ +

2v;?+«)1<Г2(4)|

ii±^|o^2(OI-

Поскольку

для

времени переходного процесса верна оценка сверху

1=1

ki-k2

«=i

*l-*2

1=1

ряд Yl "'

сходится

при /с < 1, то это и

означг1ет,

что

время

Т пе-

1=0

реходного процесса ограничено. Иными словами, любая фазовая тра-

ектория "скручивается"

нуль

за

конечное время,

что и

проясняет

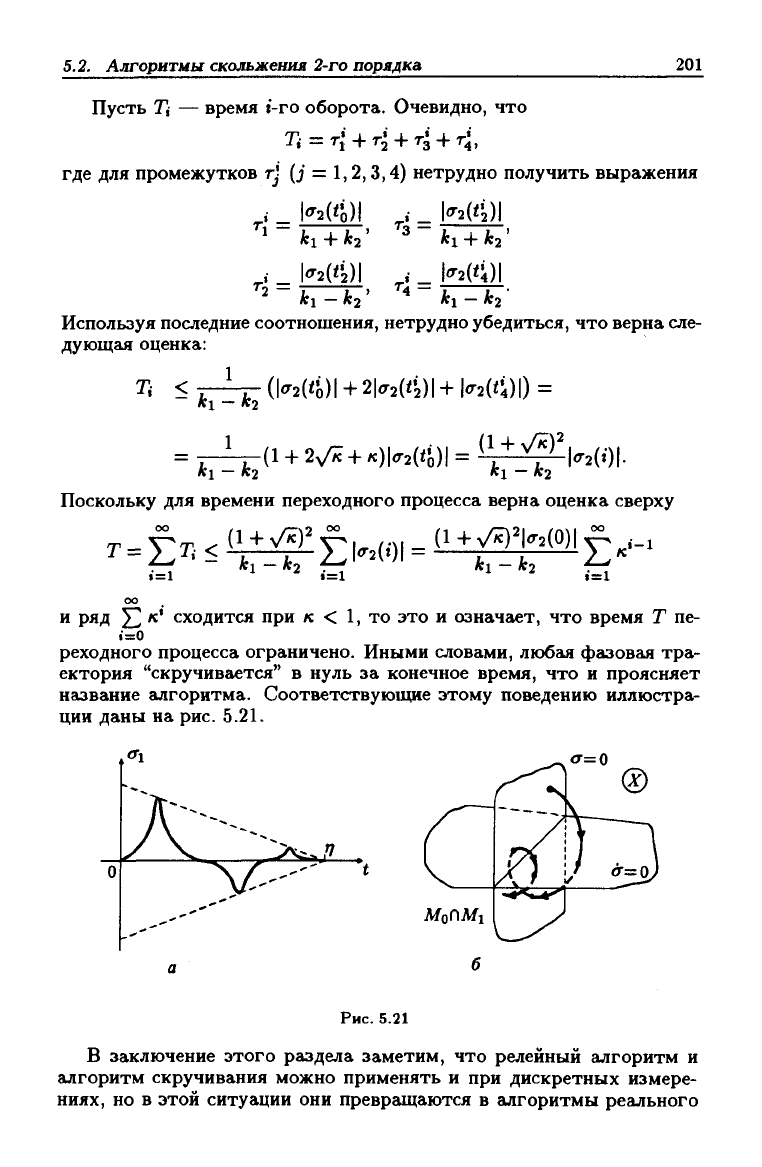
название алгоритма. Соответствующие этому поведению иллюстра-

ции даны

на

рис.

5.21.

cri

<т=0

^z:*^

М0ПМ1

Рис.

5.21

В заключение этого раздела заметим,

что

релейный алгоритм

алгоритм скручивания можно применять

и при

дискретных измере-

ниях,

но в

этой ситуации

они

превращаются

алгоритмы реального

202 Глава 5. Скользящие

режимы

высших порядков

скольжения 2-го порядка. Именно, пусть t,- — моменты измерения

функции (r(t) с постоянным шагом h = t.+i

—

t,-. Тогда релейный ал-

горитм реального скольжения 2-го порядка задается выражением

u{t) = д - кsgn[Si(Ti -g{(Ti{ti))], t е [ti,ti+i],

где

Si(Ti

= (Ti{ti)

—

<Ti{ti-i), a алгоритм дискретного скручивания, со-

ответственно, — выражением

u{t) = -kisgnai{ti) - k2Sgn[6i(ri], t G [<.,t.+i].

5.3.

Финитная стабилизация по выходу

Вновь рассмотрим задачу финитной стабилизации в нуле Е-систем1^

с уравнением выхода

(т

•= ai.

Удобно уравнения Е-системы свести к одному уравнению второго

порядка а = и. Зададимся обратной связью вида

=—kisgntr

—

r—rrjT&,

fci.fcj = const > о, (5.22)

особенность которой состоит в том, что коэффициент демпфирования

Jt2/|<^P^^

в уравнении замкнутой системы

<^+ГТГ72'^ + ''18«п<' = 0 (5-23)

неограниченно нарастает при приближении к многообразию скольже-

ния

Мо = {х\(т{х) = 0}.

Именно с этим "физическим" эффектом связаны надежды на финитно

стабилизационные возможности обратной связи (5.22).

Перейдем к анализу уравнения замкнутой системы (5.23). Прежде

всего замечаем, что при замене

<г —^ —<т

вид уравнения, а значит, и его

фг13овые траектории сохраняются, поэтому достаточно ограничиться

анализом его решений при ег > О, так как траектории в квадрантах

<т<г >

О {(Т&

< 0) подобны.

Качественно фазовые траектории исследуемого уравнения

•^

+ ПлП^ + fci sgn

от

5.3.

Фгшитная

стабилизация по выходу

203

представлены на рис. 5.22, на котором

&о

— начальное значение ско-

рости,

СГ2

— точка второго пересечения фазовой траектории с осью

<т

(т.е. второго пересечения многообразия Мо), &, = <т(<») — ми-

нимальное значение скорости на интервале движения [<i,<2]. где <i —

момент обнуления скорости & (т.е. момент максимального удаления

изображающей точки от многообразия Мо), <2 — момент попадания

на Мо. При

<т

имеем дело с уравнением

ff + —^& + ki = О,

л/cr

которое нетрудно преобразовать к виду

а затем, так как при < = О верны равенства

&(0) =

&о,

<т(0) = О, после интегрирования по-

лучаем соотношение

Рис.

5.22

+ kit +

2k2<T^^^

(ro.

(5.24)

При

из (5.24) находим (учитывая, что <T(<I) = 0)

kiti + 2/r2<Tj = &о.

Поскольку ti > О, то из последнего равенства имеем первое из необ-

ходимых нам далее неравенств, именно:

1/2 <Го

(5.25)

Подставим t = t» в (5.23). Тогда, учитывая, что

<T(t,)

= О, получим

равенство

L • 1 L 1/2 n 1/2 ^^2 .

k2a;+ki(T,' =0, или <т, =

—

—-о-,.

Но очевидно (рис. 5.22), что а» <a-i, &, <

&2,

а поэтому из последнего

равенства получаем цепочку неравенств

1/2 .^ 1/2 *2/ •

^ ^^2/ .V

из которых можно извлечь второе из требуемых соотношений, именно:

-&2 < Р-(г\'\ (5.26)

«2

204 Глава 5. Скользящие

режимы

высших порядков

После подстановки (5.25) в (5.26) получаем следующее неравенство

между скоростями двух последовательных пересечений многообразия

скольжения MQ:

&о ^ 2Jfc2-

в силу отмеченной выше симметрии уравнений замкнутой системы

аналогичное неравенство имеет место для любых двух последователь-

ных моментов пересечения многообразия MQ, т.е. справедливо нера-

венство

<!•

Отсюда получаем оценку вида |<т,| < 7'|'''о|> и если выполнено условие

7= — <1

то стабилизируемость доказана, так как при этом

|(7,|

->^ О, < -)• 00,

а из неравенств типа (5.25) следует также, что и

|<г,| -> О,

-> оо,

где at — максимумы отклонений от многообразия скольжения

•

Докажем теперь, что время переходного процесса конечно. Для

этого подставим t = t2 в уравнение (5.24). Получим равенство

и, следовательно, для промежутка времени Ti = f2

— О

между двумя

пересечениями многообразия

имеет место следующая оценка:

&0-&2 1+7

Jl — '2 — Г < О-О—, .

«1 «1

Естественно, что аналогичная оценка справедлива для каждого 1-го

интервала, т.е.

«1

Но время Т переходного процесса конечно, так как в неравенстве

1 + 7

i=l ' 1 = 1

^=Е^.<т^Е1'-1

по докгизанному ранее

|<г.|<

71^.-11,

0<7<1,

оо

и, значит, ряд Y1 \'^i\ ограничен.

«•=1

5.3.

Финитная стабилизация

по выходу

205

Таким образом, имеет место финитная стабилизация S-системы

обратной связью вида (5.22). Проведенное исследование обосновы-

вает рис. 5.23, на котором изображен финитный переходный процесс,

заканчивающийся к моменту времени

т).

Рис.

5.23

в завершение данного раздела укажем причину, по которой обрат-

ная связь

и = —ki dsgn

<r —

|^|l/2

названа обратной связью по выходу. Дело в том, что поведение ис-

следуемой выше Е-системы и нижеследующей системы, описываемой

интегродифференциальным уравнением

f t

&{t) = —ki I sgn crdr

—

k^ I \(r\^'^sgn adr + ao,

0 0

суть одно, но для реализации управления, стоящего в правой части

последнего уравнения, требуется информация только о выходе

<т.

Разумеется, все выводы сохраняются и в случае использования

обратной связи вида

и = -kisgn(T-k27-r-,

</)<!.

Наконец, заметим, что все изложенные выше результаты без суще-

ственных изъятий могут быть перенесены на произвольный порядок

скольжения. Следует, однако, отметить тот факт, что при управлении

неопределенной системой информация о переменных (Т,- (г > 1) может

отсутствовать, а их оценивание с помощью стандартных наблюдений

может оказаться невозможным. Это серьезная и пока не решенная

проблема.

Глава 6

Теория операторной обратной связи

в данной главе свойства систем стабилизации из главы 3 улучшаются

путем использования дополнительной нелинейной обратной связи опе-

раторного типа. Напомним, что "по легенде" операторная обратная

связь должна обеспечить "сближение" динамических свойств задат-

чика и системы управления с координатной и координатно-оператор-

ной обратными связями. Подобное сближение требуется осуществить

без использования какой-либо информации о факторах неопределен-

ности, а только путем установления дополнительной нелинейной связи

между переменными системы. Результатом использования такой не-

линейной связи должно быть повышение качества переходных процес-

сов и уменьшение их зависимости от факторов неопределенности.

6.1.

О назначении операторной обратной связи

В теории координатно-операторной обратной связи (глава 4) рассмо-

трены различные алгоритмы стабилизации простейшего неопределен-

ного объекта

i = 2d^ +

b(ji

+ a (6.1)

с неизвестными параметрами, принадлежащими известным множе-

ствам

а£А, ЬеВ.

Одним из наиболее эффективных и простых в реализации оказался

пропорционально-интегргшьно-релейный закон стабилизации

sgni dt, (6.2)

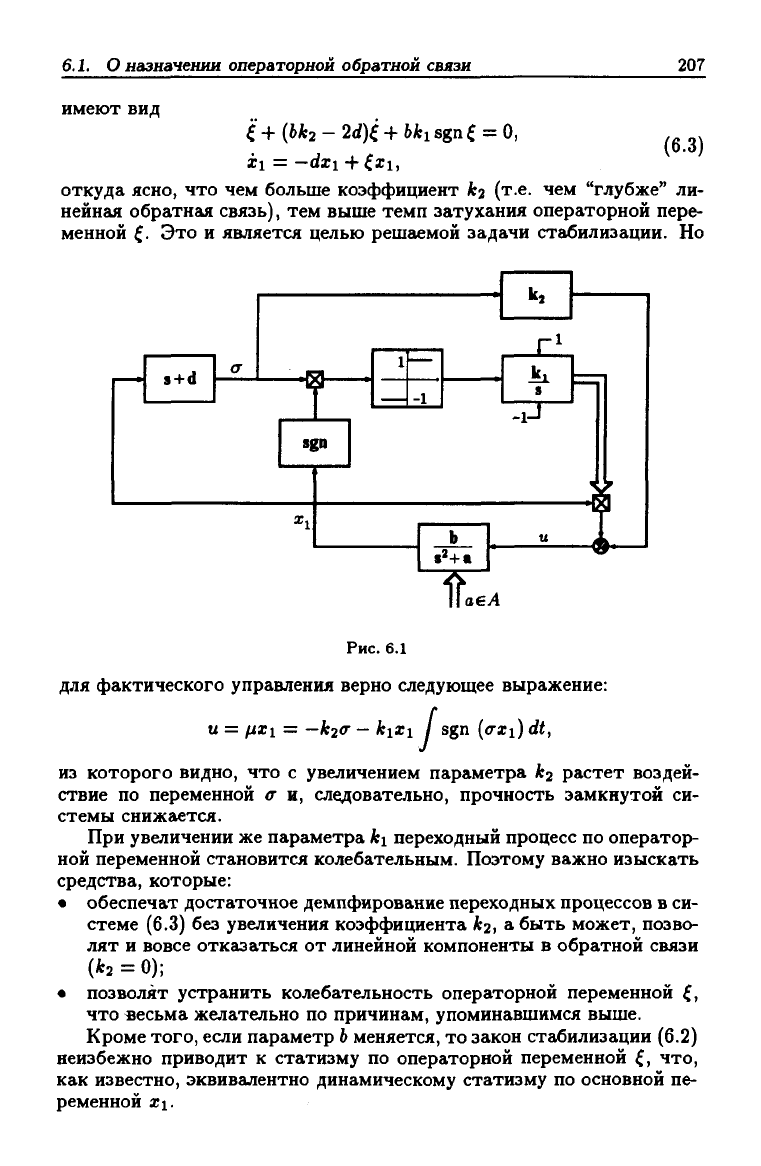
где ki,k2 — фиксированные параметры обратной связи. Структурная

схема соответствующей замкнутой системы (6.1), (6.2) приведена на

рис.

6.1 (смысл стрелок на интеграторе в законе (6.2) будет пояснен

позднее). Уравнения движения замкнутой системы в пределах линей-

ной зоны интегратора (рис. 6.1) и при постоянных параметрах а и

Ь в координатно-операторном пространстве следуют из (6.1), (6.2) и

6.1.

о назначении

операторной обратной

связи

207

(б.З)

имеют вид

^ + (6*2 - 2d)i +

6*1

sgn^ = О,

xi = —dxi +^xi,

откуда ясно, что чем больше коэффициент jfcj (т.е. чем "глубже" ли-

нейная обратная связь), тем выше темп затухания операторной пере-

менной ^. Это и является целью решаемой задачи стабилизации. Но

» + d

•V.

sgn

-1

к»

Г'

.,J

Ч«

•^

. .

аеЛ

Рис. 6.1

для фактического управления верно следующее выражение:

и = fixi =

—к2(г

- kixi / sgn

{(TXi)

dt,

из которого видно, что с увеличением параметра *2 растет воздей-

ствие по переменной <т и, следовательно, прочность замкнутой си-

стемы снижается.

При увеличении же параметра к\ переходный процесс по оператор-

ной переменной становится колебательным. Поэтому важно изыскать

средства, которые:

• обеспечат достаточное демпфирование переходных процессов в си-

стеме (6.3) без увеличения коэффициента ki, а быть может, позво-

лят и вовсе отказаться от линейной компоненты в обратной связи

(*2 = 0);

• позволят устранить колебательность операторной переменной ^,

что «есьма желательно по причинам, упоминавшимся выше.

Кроме того, если параметр 6 меняется, то закон стабилизации (6.2)

неизбежно приводит к статизму по операторной переменной ^, что,

как известно, эквивалентно динамическому статизму по основной пе-

ременной XI.

208

Глава 6. Теория

операторной

обратной связи

Отметим, без подробного комментария, что изменения параметра

а с ограниченной скоростью, т.е. когда

\а\ < const < bki,

закон (6.2) допускает. В связи с этим возникает вопрос о принци-

пиальной достижимости сформулированных выше целей упраления и

путях их достижения.

Можно, конечно, анализируя уравнение (6.1)

^ =

2d^

+ а,

попытаться угадать соответствующий алгоритм стабилизации опера-

торной переменной ^ в нуле, что, конечно, возможно. Но кажется бо-

лее предпочтительным попытаться воспользоваться рекомендациями

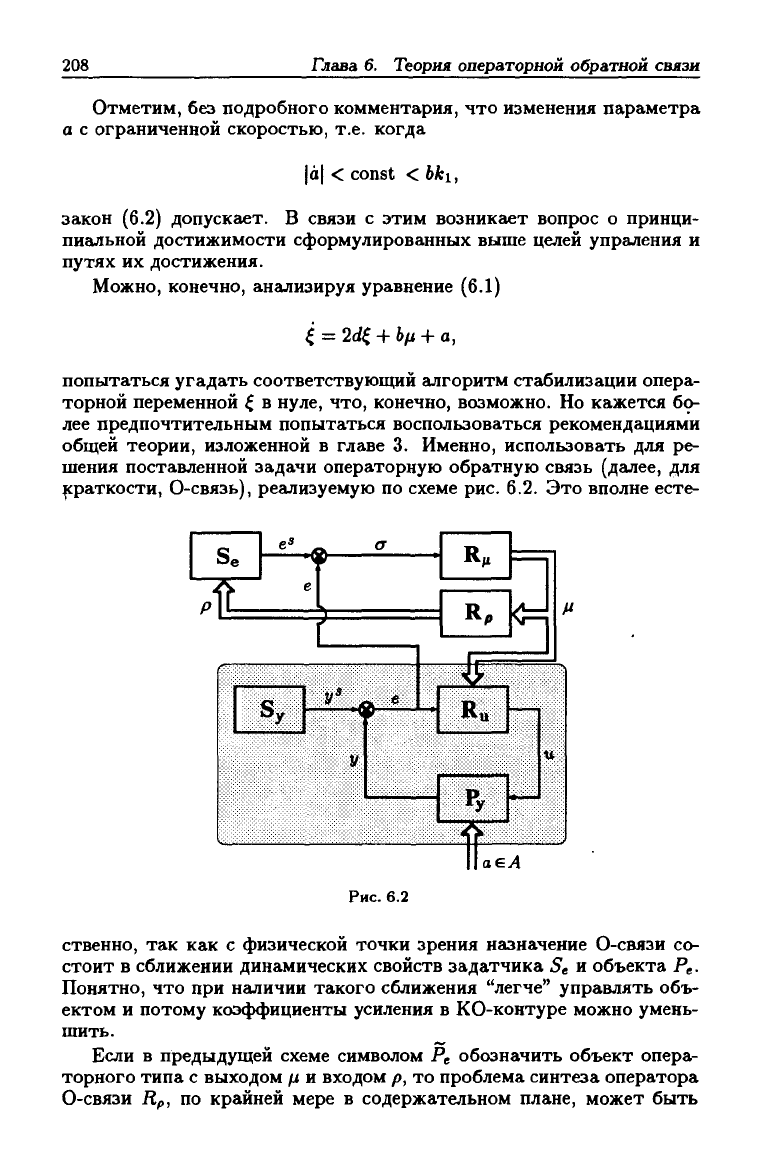
общей теории, изложенной в главе 3. Именно, использовать для ре-

шения поставленной задачи операторную обратную связь (далее, для

краткости, 0-связь), реализуемую по схеме рис. 6.2. Это вполне есте-

Рис.

6.2

ственно, так как с физической точки зрения назначение 0-связи со-

стоит в сближении динамических свойств задатчика 5е и объекта Р^.

Понятно, что при наличии такого сближения "легче" управлять объ-

ектом и потому коэффициенты усиления в КО-контуре можно умень-

шить.

Если в предыдущей схеме символом Ре обозначить объект опера-

торного типа с выходом

/л

и входом р, то проблема синтеза оператора

0-связи Rp, по крайней мере в содержательном плане, может быть

6.2.

Уравнения движения

209

сведена к стандартной проблеме синтеза обратной связи, которую ил-

люстрирует рис. 6.3. Разумеется, при этом проявятся важные особен-

.1—^

Р ^ •

Рис.

6.3

ности В управлении таким объектом, и прежде всего принципиальна

нелинейность его уравнений движения. Поэтому в первую очередь

получим уравнения движения исследуемой системы, поскольку пара-

метры d эадатчика Se в схеме на рис. 6.2 теперь переменны и зависят

от р, т.е. dp = d{p), и если р = p{t), то dp = dp{t).

6.2. Уравнения движения

в пространстве координата-оператор

Напомним, что в исходном (ri, а;2)-координатном пространстве ста-

билизируемый объект описывается следующими уравнениями:

XI = Х2, Х2 = axi + bu.

Следуя общей процедуре синтеза бинарного управления, введем

КО-ошибку

сГр

Х2

+ dpXi = xi + dpXi,

которую впредь будем помечать индексом р, отличая ее тем самым от

прежней ошибки

<г

= хз + dxi. Теперь можно определить в области

Gs = { (хьагз) I

\<г\

5\xi\,

S = const }

новую операторную переменную

^ =

сгр/х1.

(6.4)

Для перехода к описанию в координатно-операторном, далее, для

краткости, КО-пространстве («i,^) потребуется уравнение изменения

операторной переменной ^. Дифференцируя выражение (6.4) и исполь-

Zf.

- dpXi _

210 Глава 6. Теория

операторной обратной

связи

зуя равенства х^ = ахх + Ь«,

Х2

<Гр —

dpXi, имеем последовательно:

с _ ^Р "'р *1 _ iC2 + dpX2 + dpXl ^

Xl Xi Xi Xi

_ axi + bu +

dp(Tp

- rfjzi + dpXi

~ Xl

= 2rf^ + 6—+ (a-rf2)+d^_^2.

Если, как и ранее, использовать в главном контуре простейшую

бинарную операцию и = fixi и рассматривать стабилизацию в малом,

когда можно пренебречь квадратичными членами, то искомые урав-

нения можно записать в следующем виде:

xi — -dpXi+ixi,

i = 2dp( + bp + a-dj + dp. ^ • '

Эти уравнения отличаются от применявшихся ранее уравнений

xi = -dxi+^xi,

i = 2d( + bfi + a-d^

зависимостью параметра d задатчика Se от операторной переменной

р и наличием производной dp^O ъ правой части (6.5), так как теперь

dp = dp{t). Поскольку 0-закон (т.е. функцию р) можно формировать

независимо от КО-закона (т.е. функции (х), постольку член dp, по

существу, можно интерпретировать как дополнительное управление,

привлекаемое для стабилизации 0-переменной ^ в нуле.

Практически, однако, удобно синтезировать не производную dp,

а при выбранной функциональной зависимости d{p) (например, без

потери общности, в виде dp = d + р) оператор 0-связи Rp (рис.6.2) и,

в отдельных случаях, оператор КО-связи R,,.

Для дальнейшего упрощения уравнения Ре-объекта (рис. 6.3) и по-

лучения его окончательного вида будем считать, что при всех из-

менениях параметр р мал по отношению к d. Это предположение

вполне оправдано, более того, нужно стремиться к его обеспечению,

поскольку в желаемом режиме стабилизации, когда 'р = О, основная

переменная xi изменяется, согласно (6.5), в соответствии с уравне-

нием

Xl = -dpXi = -{d + p)xi.

Тогда качество переходного процесса близко к эталонному, опре-

деляемому уравнением ij = —dxi, если выполнено упомянутое выше

соотношение порядка между параметрами dn р. Но если принять это

допущение, то можно приближенно заменить

dp = (d + p)^d^ + 2dp.