Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

5.1.

Предварительные

сведения

181

в режиме скольжения (т = О, то искомый фазовый вектор должен удо-

влетворять уравнению

где V(T — градиент функции

(т{х)

в точке х. Решая последнее урав-

нение относительно параметра а, находим

(V<T, (/--/+))•

Соответствующее дифференциальное уравнение имеет вид

= и. =f--a*if--f+) =

и описывает движение по поверхностям уровня а{х) = const. Для

получения уравнения скольжения нужно дополнить его равенством

«г

О,

€ Mgi.

Уравнениям скольжения

i = fsi{x), <т(ж) = 0, а:€М,1

можно придать полезную геометрическую интерпретацию. Введем в

рассмотрение на многообразии М оператор

Р{х) = Е-

f-{x)-f+{x){V<T{x),{.))

{V<T(x),{f-(x)-f+(x))) •

Поскольку Р'^ = Р, то этот оператор является оператором локального

проектирования на многообразие с =

вдоль прямой (параллельно),

задаваемой вектором Д/ = /"

—

/+ (рис. 5.3). Поэтому уравнения

Рис. 5.3

скольжения можно записать в виде

^ = Рд/Г, Рм = Е-

А/(У<т,(-))

(V<r,A/)

182 Глава 5. Скользящие

режимы

высших порядков

Для рассматриваемого уравнения х = f + Ьи вектор

Д/ = / + Ьи~ - f-

Ьи"^

= Ь(и~ - и"*") = ЬАи,

и если Ди ф О, то векторы Д/ и 6 коллинеарны. Следовательно, верно

равенство

а так как по свойству оператора проектирования

b(Va,b)

'^•'-(-^>='-

= 0,

<V<T,6)

то уравнения скольжения можно записать в более компактном виде:

= Pbf, (7 = 0, l€Msl.

5.1.2. Об инвариантности уравнения скольжения

по отношению к возмущениям,

удовлетворяющим условию согласованности

Напомним, что внешнее возмущение

<p{t,

х) удовлетворяет условию со-

гласованности (МС-условию), если оно действует в канале управления

x = f + b{u +

(p).

(5.1)

В силу указанного выше свойства

РьЬ

= 0.

Уравнения скольжения по многообразию М для возмущенного (5.1) и

невозмущенного

= f +

Ьи

объектов совпадают и даются формулами

x = Pbf,

<г

= О, х£ Msi С М. (5.2)

Именно этот математический факт проясняет тот интерес, кото-

рый постоянно проявляется в теории управления и ее приложениях к

идее интегргшьного многообразия и ее реализации с помощью разрыв-

ной и глубокой обратных связей.

Здесь уместно заметить, что уравнения (5.2) описывают также

движение в системе с глубокой обратной связью

= f +

Ьи

= / -

кЬ(т,

к = const > О, (5.3)

и=—к<7

Т.е. при устремлении коэффициента обратной связи в бесконечность

{к -> оо), если выполнено условие

(Vff,b)>0.

5.1.

Предварительные

сведения 183

Для того чтобы убедиться в этом, можно воспользоваться при-

веденными выше геометрическими соображениями или нижеследую-

щими выкладками. В силу уравнения движения находим

& = {V<Tj)-k{V,(T,b)a, (5.4)

и при указанных выше условиях изображающая точка "мгновенно"

достигает поверхности а(х) =

и далее ее не покидает, а значит, во

время движения имеет место равенство

О-

Воспользуемся теперь

следующим эвристическим приемом: выразим из уравнения

про-

изведение

к<т,

а результат подставим в уравнение (5.3), тогда получим

уравнение

которое вместе с равенством

<т

и задает уравнение движения си-

стемы с глубокой обратной связью. Видно, что оно совпадает с полу-

ченным выше уравнением скольжения разрывной системы.

В определенной степени стандартную разрывную систему и си-

стему с глубокой обратной связью можно рассматривать как два по-

люса реализации одной и той же идеи — идеи скольжения по гладкому

многообразию. В одном случг1е это скольжение осуществляется беско-

нечно гладко, а в другом — с разрывом уже первой производной функ-

ции, задающей поверхность скольжения. Оказывается, что между

этими двумя крайними системами существует бесконечно много си-

стем, "скользящих" по той же поверхности, но обладающих различной

степенью гладкости. О некоторых таких промежуточных системах и

идет речь в данной главе.

5.1.3.

Уравнения реального скольлсения

Практически, т.е. в реальных ситуациях, переключения разрывного

элемента происходят не точно на многообразии М = {г ] <т(г) = О},

но всегда в некоторой его окрестности

0(М) ={х|Их)|<Л(Д)},

где А(А) — "амплитуда" отклонения траекторий разрывной системы

i = /^ от многообразия М (рис. 5.4). Здесь и далее Д — параметр.

Рис. 5.4

184

Глава 5. Скользящие режимы высишх порядков

характеризующий неидеальность переключении, например временную

или пространственную задержку, быструю немоделируемую динами-

ку и т.п. Подобный режим скольжения принято называть реальным

скользящим режимом. При малых амплитудах А(А) его можно также

характеризовать "частотой" переключения W(A), для которой верна

оценка

W(A)

< ^М.,

^^- 2Л(Д)'

где II/II = min(||/~||, ((/•'"II). При устранении неидеальности пере-

ключения (т.е. при Д

—>

0) "амплитуда", как правило, уменьшается

до нуля, а "чгютота" растет до бесконечности, т.е.

lim W(A) = оо,

Д-vO

lim А{А) = 0.

Д-fO ^ '

При этом реальное скольжение переходит в идеальное (рис. 5.5)

и весьма важен вопрос о порядке этого перехода по параметру Д.

о-=0

Рис. 5.5

Прежде чем точно определить то, что здесь имеется в виду, полу-

чим уравнения реального скольжения. Напомним, что при идеальном

скольжении

(а-

= 0) искомый фазовый вектор правой части уравнения

движения /eq (рис. 5.5) находится в результате решения уравнения

<r = (Vo-,/ec,) = 0.

При реальном скольжении выполнено неравенство |<т| < А{А), и

искомый вектор правой чг1сти системы реального скольжения /„ на-

ходится из неоднородного уравнения

= (V<r,/„).

В частности, если система имеет вид

x = f +

b{a

!fi),

(5.5)

то последнее уравнение можно переписать следующим образом:

(Г

(V<T,

Н-

(V<r,

Ь)и„ + (Vtr,

b)<p.

5.1.

Предварительные

сведения 185

Если {Vo-,6)^0, то

(У<г,/) &

""- {Va,b) ^ (Va,b) ^'

и после подстановки найденного значения в уравнения движения (5.5)

находим

{Va,b) (V<r,6>-

Если использовать оператор проецирования

(V<T,

то последнее уравнение принимгьет вид

^ = ^^-^ + ^(V^ ^'-'^

и вместе с ограничением

к1 < А(А) (5.7)

определяет движение в реальном скользящем режиме.

Представляет интерес исследование близости решений идеального

и реального скольжения (обозначим их Xid(t) и x(t) соответственно),

выпущенных из одной начальной точки х° £ М при одном и том же

возмущении

<p{t).

Решение идеального скольжения описывается урав-

нениями

iid = Pbfixid), cr(xid) = О,

а решение реального скольжения имеет вид

х = Рь/{х) +

-^^^-^&,

\а(х)\<А(А).

Положим для простоты и без потери общности, что вектор

П = 7= ГТ- = const ,

<Va,6)

тогда оператор Рь = const, и после вычитания первого уравнения из

второго для ошибки е = X

—

Хи получаем следующее уравнение:

£ = Рь[ f{xid +£)- f(xid)]-\-h&.

По теореме Лагранжа для некоторого вектора 0 G [a^id, ^^id + е]

имеет место равенство

f{xid+e)-f{xid) = ^{e)e,

186 Глава 5. Скользящие режимы высших порядков

поэтому впредь имеем дело с уравнением вида

Поскольку е(0) = О, то последнее дифференциальное уравнение

эквивалентно интегральному уравнению

t t t

£{t) = /Ме{т)dT + h f &dT= f ЛГе(г)dr + h(r{t).

0 0 0

Полагая, что на некотором отрезке

[О,

Т]

\т

от интегрального уравнения переходим к скалярному неравенству для

нормы ошибки

11Ф)11<^^/|Иг)||йг + ||Л||Л(Д).

После применения леммы Гронуолла-Беллмана находим на отрезке

[О,

Т] искомую оценку

Таким образом, из принадлежности траекторий реального сколь-

жения окрестности многообразия М

0{М)={х I |о-|<Л(Д)}

следует их близость на конечном интернете времени к соответствую-

щим траекториям идеального скольжения с точностью порядка А(Д),

т.е.

с точностью реешьного скольжения. Отсюда следует, что

• нужно стремиться к повышению порядка реального скольжения

по отношению к параметру Д, ибо тогда большей точности при-

ближения к идеальному скольжению можно добиться при большей

неидеальности.

Иными словами, это и есть прямой путь к повышению прочности си-

стемы управления.

Аналогичная проблема возникеъет при дискретном моделировании

разрывных систем, когда роль параметра неидеальности выполняет

шаг дискретизации временной шкалы

5.1.

Предваритедьньге сведения 187

и разрывы имеют место на множестве дискретных моментов времени

{tj}.

В этом случае окрестность 0{М) реального скольжения харак-

теризуется неравенством

W{tj)\<A(h)

и для повышения точности моделирования нужно уменьшать шаг дис-

кретизации h, но тогда растут вычислительные затраты. Выгоды от

уменьшения Л возрастают с ростом порядка малости функции Л(Л)

по Л, т.е. чем выше число г в соотношении

A{h) ~ Л^

тем более высокая точность счета достигается при заданном шаге

интегрирования h.

Проведенные рассуждения актуализируют данную проблему изы-

скания средств повышения порядка функции А{А) по малому параме-

тру Д, определяющему "точность" реального скольжения.

5.1.4. Замечание о порядке скольхсения

От чего же зависит и чем определяется порядок скольжения?

Для ответа на этот вопрос рассмотрим движение в скользящем

режиме разрывной системы

i = f^{x) = f{x) + b(x)u^{x) (5.8)

по гладкому многообразию

Мо={х\

(т{х)

= 0} . (5.9)

Из (5.8), (5.9) имеем равенства

= {V<T,/±) = (V<r,/)-KV<T,6)u±, (5.10)

и если векторные поля /*(х) трансверсальны Мо, то (Vcr, b)|^^ т^

на многообразии Мо возможен скользящий режим. При этом

«г

^^q = (V(T,/)-l-{V(T,b)Ueq = 0. (5.11)

Вычитав (5.11) из (5.10) при

<т — О

я вводя обозначения

получаем

« - Ueq,

{Va,b)uf.

<7=0

Напомним, что с такими уравнениями мы ранее уже имели дело и

анализировали их свойства при наличии неидеальности переключений.

188

Глава 5. Скользящие режимы высших порядков

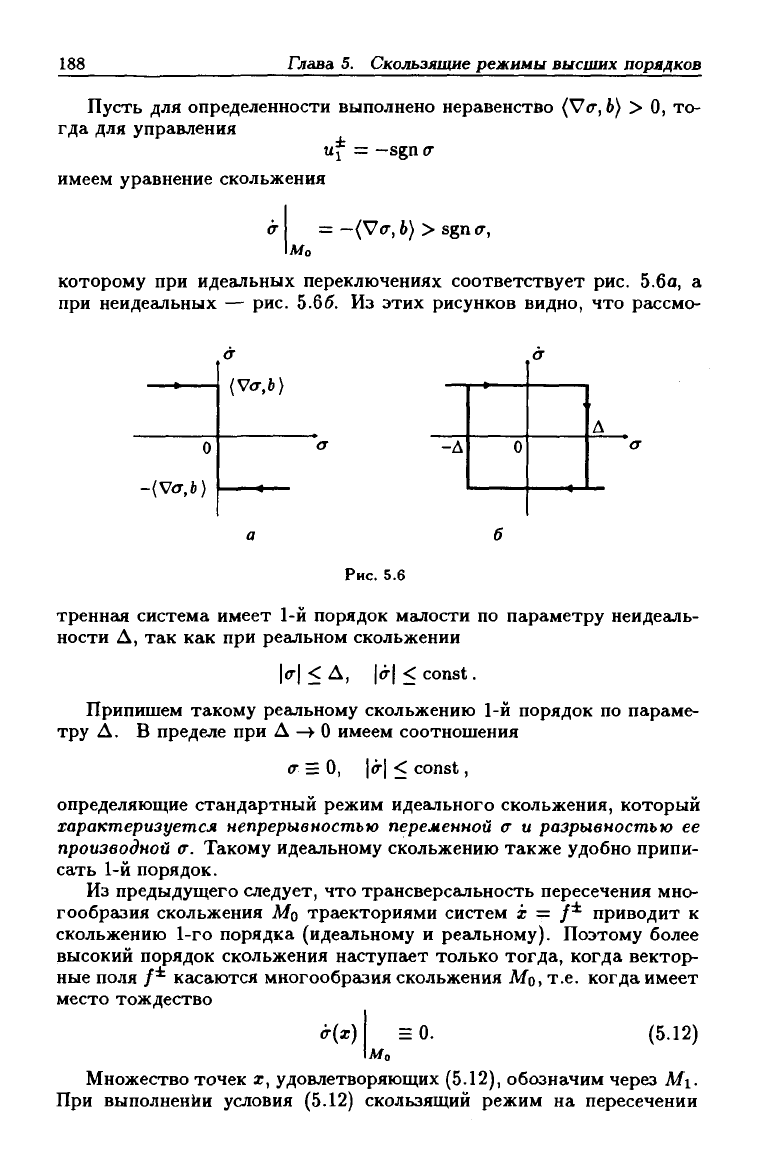
Пусть для определенности выполнено неравенство

(V(T,

6) > О, то-

гда для управления

—sgniT

имеем уравнение скольжения

= -{V<T,b) >sgn<r,

которому при идеальных переключениях соответствует рис. 5.6а, а

при неидеальных — рис. 5.65. Из этих рисунков видно, что рассмо-

-(Vo-,6)

(Va-,6)

-А

Рис.

5.6

тренная система имеет 1-й порядок малости по параметру неидеаль-

ности Д, так как при реальном скольжении

\сг\

< А,

\&\

< const.

Припишем такому реальному скольжению 1-й порядок по параме-

тру Д. В пределе при Д

—> О

имеем соотношения

<т

= О, jo"! < const,

определяющие стандартный режим идеального скольжения, который

характеризуется непрерывностью переменной

<т

и разрывностью ее

производной а. Такому идеальному скольжению также удобно припи-

сать 1-й порядок.

Из предыдущего следует, что трансверсальность пересечения мно-

гообразия скольжения MQ траекториями систем i = /* приводит к

скольжению 1-го порядка (идеальному и реальному). Поэтому более

высокий порядок скольжения наступает только тогда, когда векторь

ные поля /* ка^саются многообразия скольжения Мо, т.е. когда имеет

место тождество

сг(х)

= 0.

Мо

(5.12)

Множество точек х, удовлетворяющих (5.12), обозначим через Mi.

При выполнении условия (5.12) скользящий режим на пересечении

5.1.

Предварительные

сведения

189

Mo n Ml может возникнуть, если разрывна и знакопеременна вторая

производная

ir =

(V<7,

/±) =

(V<T,

/> + {V&, 6)u±,

т.е.

(V<T,

6) ^

на Mo n Ml.

Сказанное иллюстрируют рис. 5.7. На рис. 5.75 показан ход тра-

екторий такой системы при взгляде с торца на пересечение

Поскольку в этом случае функции а и

непрерывны, а функция ir раз-

МоПМг 2

Рис. 5.7

рывна, то в идеальном скользящем режиме имеем соотношения

<т

= 0,

(7 = О, |<г| < const. Следуя принятой выше концепции, такому режиму

скольжения нужно присвоить 2-й порядок.

Для определения порядка режима реального скольжения по пара-

метру неидеальности Д допустим, что при достаточно малом Д > О

реальный скользяш;ий режим удерживается в окрестности пересече-

ния Мо П Ml, т.е. при некоторых константах Ло(Д), Л1(Д), Лз (Д)

имеют место следующие неравенства:

\а\<Ао{А),

И<Л2(Д), А- <\&\<А+{А),

(5.13)

причем

Ит Ло(Д) = lim Л^Д) = О,

д->о д-».о

lim Л^(Д)>0.

д->о ^ ^ '

Пусть г(Д) — какой-либо интервал неопределенности а. Ясно,

что г(Д)

—> О

при Д

—>

0. Тогда по теореме Лагранжа для некоторой

точки в из этого интервсша

|t^(0)|

<2max|<r| <

2Л1(Д)

г(Д) •

(5.14)

190 Глава 5. Скользящие

режимы

высших порядков

Аналогично, для того же интервала находим для некоторого 6'

\<т{е')\

<2max|<r| <

2Ао{А)

г(Д) •

(5.15)

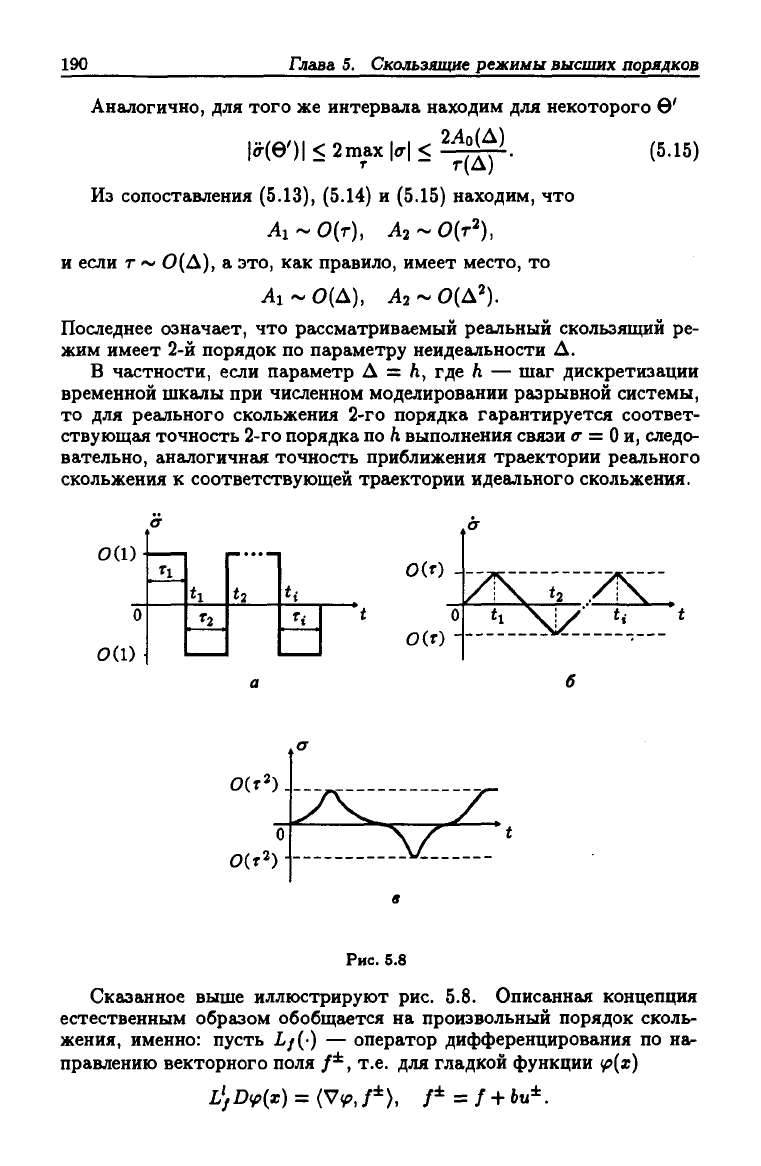
Из сопоставления (5.13), (5.14) и (5.15) находим, что

AI~0{T),

А2^0{Т^),

и если г ~ 0(A), а это, как правило, имеет место, то

Ai ~ 0(A), А2 ~ О(Д').

Последнее означает, что рассматриваемый реальный скользящий ре-

жим имеет 2-й порядок по параметру неидеальности Л.

В частности, если параметр А = h, где h — шаг дискретизации

временной шкалы при численном моделировании разрывной системы,

то для реального скольжения 2-го порядка гарантируется соответ-

ствующая точность 2-го порядка по

выполнения связи

о-

и, следо-

вательно, аналогичная точность приближения траектории реального

скольжения к соответствующей траектории идеального скольжения.

0(1)-

0(1)

Г2

«2

О(т^)

О(г')

у^"--у-^

:хг

Рис.

5.8

Сказанное выше иллюстрируют рис. 5.8. Описанная концепция

естественным образом обобщается на произвольный порядок сколь-

жения, именно: пусть Lf(-) — оператор дифференцирования по на-

правлению векторного поля /*, т.е. для гладкой функции ip(x)

L'jD<p(x) = (V<p,f'^), /± = /-h6u±.