Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

5.2.

Алгоритмы скольжения

2-го

порядка

191

При кратном применении этого оператора имеем равенство

L'f(p

= Lf {Ь'г

^(р),

I —

целое число.

Заметим, что в тех случаях, когда это имеет смысл, между произ-

водными по времени функции (х(х) и системой х = f{x) справедливо

следующее равенство:

dfc

Пусть при последовательном дифференцировании функции

<т{х)

все ее производные до порядка (г

—

1) включительно непрерывны, а

г-я производная

о-^'')

IJ(T

разрывна и знакопеременна. Тогда, если

пересечение

Mr =

Мо П

Ml П ...

Мг_1,

где

М, = {I|<T(')(X) = 0}, / =

0,1,...,Г-1.

не пусто, то оно является многообразием идеального скольжения по-

рядка г.

Если, кроме того, при реальном скольжении обеспечено выполне-

ние следующих неравенств для / = 0,1,

...,г—1:

|<г(')|<Л(Д), кМ|<Лг(Д), >lr(A)>const >0,

где А — параметр, характеризующий неидеальности переключений,

то точность реального скольжения по

(г

имеет порядок Д', так как

к(')|^0(дг-'), / =

0,1,...,г-1.

5.2.

Алгоритмы скольжения 2-го порядка

Рассмотрим некоторые алгоритмы скольжения 2-го порядка.

Прежде всего уточним математическую модель, с которой пред-

стоит иметь дело. Вновь рассмотрим гладкое многообразие

Мо = {х I

<т{х)

= 0}.

Поведение в его окрестности 0(Мо) разрывной системы

х = f +

bu"^

можно изучать по скалярному уравнению вида

«r

= (V<r,/)-KV(T,6)«±. (5.16)

Пусть Ueq — решение для х € 0{Мо) уравнения

0 = <V(T,/>-»-(V«r,6>Ueq, (5.17)

192 Глава 5. Скользящие

режимы

высших порядков

тогда, после вычитания (5.17) из (5.16), получим, что в окрестности

0{Мо) действует уравнение

Если обозначить правую часть последнего уравнения через и, то

тем самым изучение движений в окрестности 0(Мо) можно свести,

без ущерба для общности, к следующему стандартному уравнению:

& = и. (5.18)

Особенность такого уравнения при анализе скользящих режимов

2-го порядка состоит в том, что функция и непрерывна и такова,

что фазовые траектории исходной системы касаются многообразия в

точках скольжения 2-го порядка, иными словами, и обращается в нуль

на пересечении

MQDMI,

где,

как и раньше,

Mi = {x\ ff(z) = 0}.

Проблема стабилизации скалярного объекта (5.18) непрерывным

управлением сводится следующими заменами

к стандартной проблеме стабилизации в нуле объекта 2-го порядка

^' = ''" ''^ = "' (5.19)

(7 = (Ti,

обратной связью I/{(TI,(T2), которая при скольжении 2-го порядка мо-

жет быть и разрывной. Разумеется, наиболее привлекательны те

обратные связи I/(<TJ,<T2), которые финитно стабилизируют объект

(5.19) в нуле по выходу, однако не будем пренебрегать и асимпто-

тически стабилизирующими обратными связями по состоянию или по

выходу.

Описанная выше конструкция допускает естественное обобщение.

Так, проблема организации скользящего режима г-го порядка на мно-

гообразии

эквивалентна проблеме финитной стабилизации по вы-

ходу в нуле следующей системы г-го порядка:

о-,=(Г,+1,

i = 1,2, ... ,г-1,

(5.20)

(Тг = f,

<Т

= <Ti.

в самом деле, в этом случае в желаемом режиме имеем равенства

<т = 0-1 = 0-2 = ... = <Тг = О,

которые означают, что движение происходит по пересечению

МоПЛ/1 П...ЛЛ/г,

5.2. Алгоритмы

скольжения

2-го порядка 193

где,

как очевидно, множества М,- определяются следующими соотно-

шениями:

Mi = {x |<т<''){х) = 0}.

Порядок скользящего режима можйо связать с относительным по-

рядком исходного объекта по управлению, если за его выход принята

переменная

<т(х).

Проще всего и без потери в общности это можно по-

яснить на примере линейного стационарного объекта. Действительно,

пусть связь между входом и и выходом а объекта определена дробно-

рациональной передаточной функцией W{s) = p(s)/a{s) (рис. 5.9).

W(s)

Рис. 5.9

Тогда при относительном порядке единица, т.е. когда

dega(s) -deg/9{s) = 1,

производная

<т

может претерпевать разрывы, если управление и раз-

рывно и, следовательно, возможен скользящий режим 1-го порядка.

При условии, что

deg Q{S) - deg ^(s) = г,

функции ffC), I = 0,1, ... ,r

—

1 не зависят явно от управления, а

функция

ff^*"'

— зависит, и, следовательно, при разрывном управле-

нии и разрывы может претерпевать только

(т^''\

а значит, в системе

в принципе возможен скользящий режим не ниже г-го порядка. Та-

ким образом, порядок функции, задающей поверхность разрыва, по

управлению (т.е. номер первой производной Ли, явно зависящей от

управления) и определяет порядок скользящего режима, если, конечно,

последний устойчив.

Рассмотрим конкретные примеры алгоритмов скольжения 2-го по-

рядка подробнее.

5.2.1.

Асимптотические алгоритмы скольжения 2-го порядка

При решении задачи асимптотической стабилизации в нуле объекта

(Е-системы)

сначала исследуем возможности линейной обратной связи

и =-ki<Ti - к20-2. (5.21)

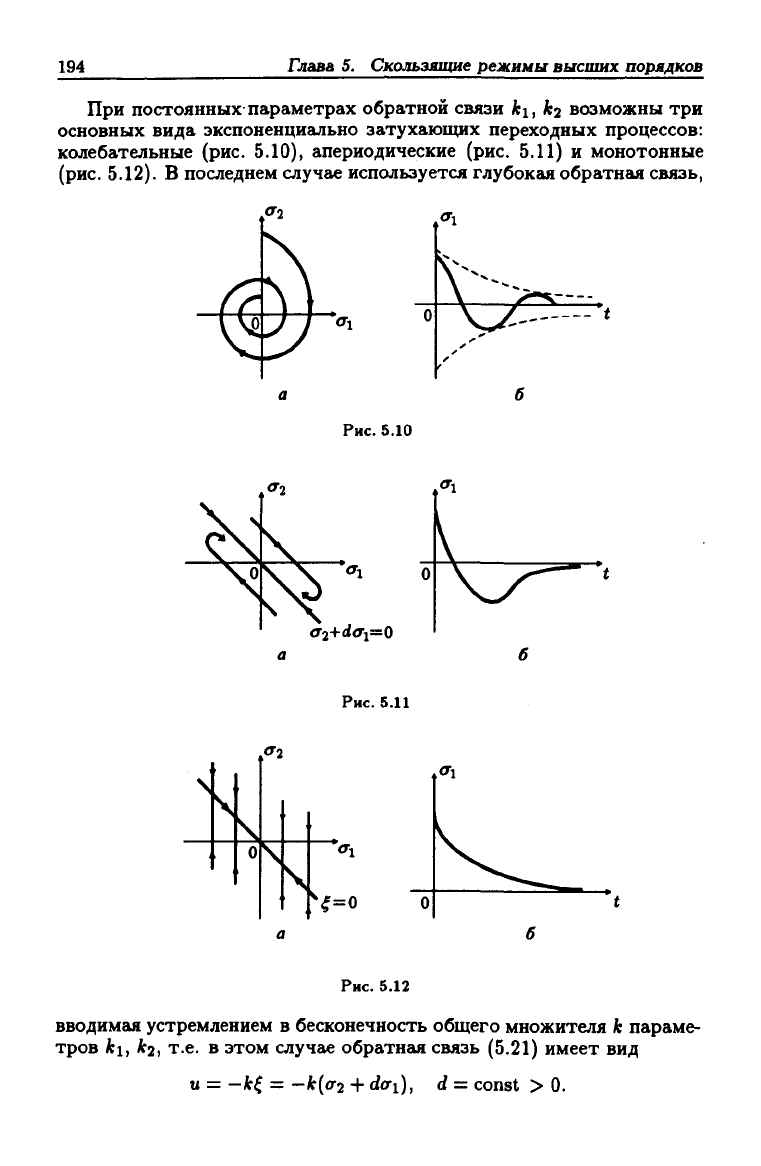
194

Глава 5. Скользящие режимы высших порядков

При постоянных параметрах обратной связи ку, ki возможны три

основных вида экспоненциально затухаюыщх переходных процессов:

колебательные (рис. 5.10), апериодические (рис. 5.11) и монотонные

(рис.

5.12). В последнем случае используется глубокая обратная связь.

Рис. 5.10

<T2+rf<Ti=0

Рис. 5.11

^=0

Рис. 5.12

вводимая устремлением в бесконечность общего множителя к параме-

тров ki, Аг2, т.е. в этом случг1е обратная связь (5.21) имеет вид

= -к^ = -к{(Г2 + dcri), d = const > 0.

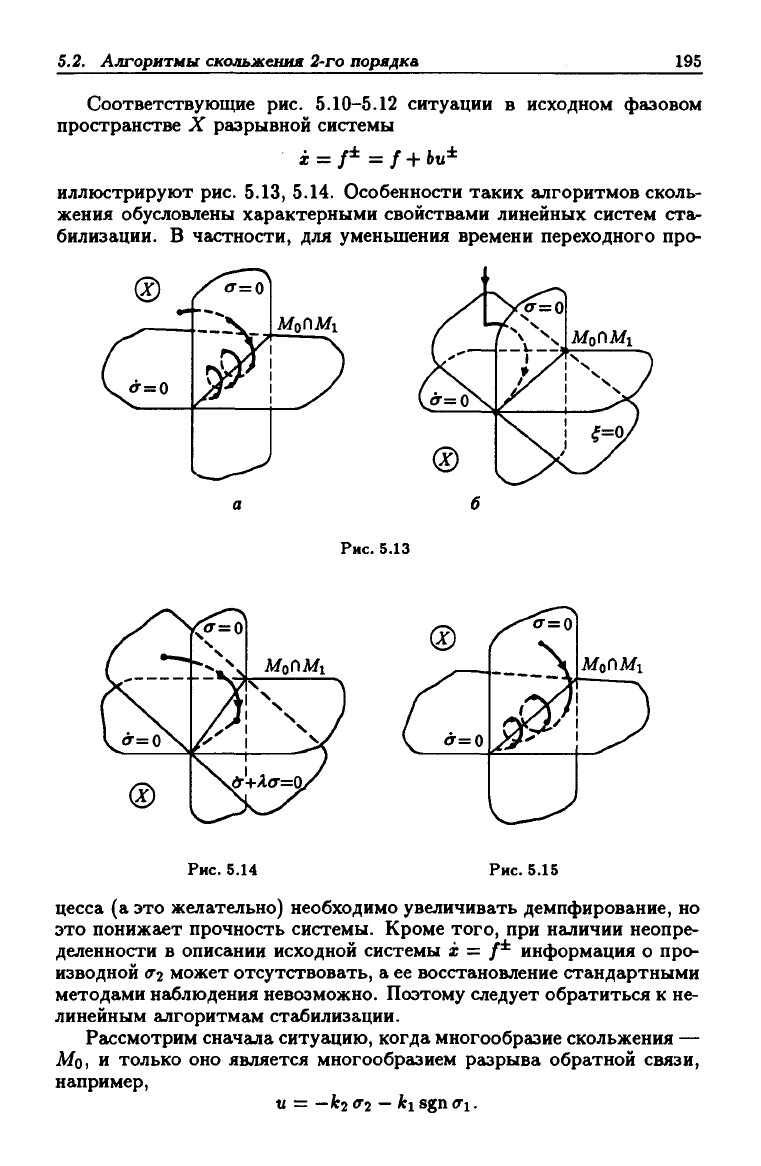
5.2. Алгоритмы скольжения 2-го порядка

195

Соответствующие рис.

5.10-5.12

ситуации в исходном фазовом

пространстве X разрывной системы

i = /± = / +

Ьи=»=

иллюстрируют рис. 5.13, 5.14. Особенности таких алгоритмов сколь-

жения обусловлены характерными свойствами линейных систем ста^

билизации. В частности, для уменьшения времени переходного про-

Рис. 5.13

Рис. 5.14 Рис. 5.15

цесса (а это желательно) необходимо увеличивать демпфирование, но

это понижает прочность системы. Кроме того, при наличии неопре-

деленности в описании исходной системы i = /* информация о про-

изводной

(72

может отсутствовать, а ее восстановление стандартными

методами наьблюдения невозможно. Поэтому следует обратиться к не-

линейным алгоритмам стабилизации.

Рассмотрим сначала ситуацию, когда многообразие скольжения —

Мо,

и только оно является многообразием разрыва обратной связи,

например,

и = -к2

<Т2 —

fci

sgn а\.

196

Глава 5. Скользящие режимы высших порядков

В ЭТОМ случае замкнутая система

= (Г2,

{Г2 — —*1

sgn

ах

- ^2 сг

асимптотически устойчива в нуле, что проверяется пробной функцией

V = kil + 2Г^^'

производная которой имеет вид

^2 2

И тождественно обращается в нуль только в начале координат. Каче-

Рис. 5.16

ственное представление о характере движения в окрестности пересе-

чения Мо П Ml в этом случае дают рис. 5.15, 5.16.

5.2.2. Разрывные асимптотические

алгоритмы скольхсения 2-го порядка

Если разрывы управления допускаются не только на многообразии

скольжения Мо, то экспоненциальную стабилизацию Е-системы в нуле

обеспечивает следующий закон СПС:

и = -fc|<Ti|sgn^,

^ =

<Г2

+ 2</(Ti, d = const > 0.

Действительно, уравнения замкнутой системы имеют вид

= <Т2,

= -A;|<ri|sgn^,

и при выполнении неравенства

k>d^

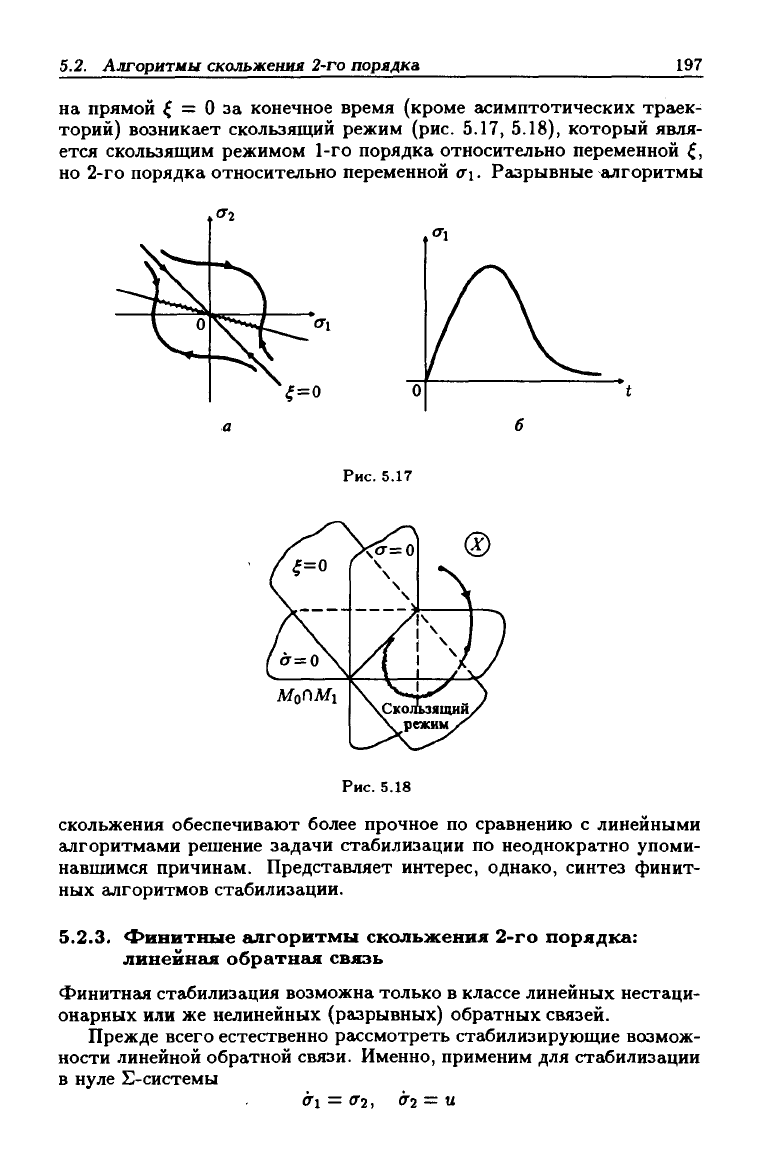
5.2. Алгоритмы

скольжения

2-го порядка

197

на прямой ^ = О за конечное время (кроме асимптотических траек-

торий) возникает скользящий режим (рис. 5.17, 5.18), который явля-

ется скользящим режимом 1-го порядка относительно переменной ^,

но 2-го порядка относительно переменной (Г\. Разрывные алгоритмы

Рис.

5.17

Рис.

5.18

скольжения обеспечивают более прочное по сравнению с линейными

алгоритмами решение задачи стабилизации по неоднократно упоми-

навшимся причинам. Представляет интерес, однако, синтез финит-

ных алгоритмов стабилизации.

5.2.3.

Финитные алгоритмы скользкения 2-го порядка:

линейная обратная связь

Финитнг^ стабилизация возможна только в классе линейных нестаци-

онарных или же нелинейных (разрывных) обратных связей.

Прежде всего естественно рассмотреть стабилизирующие возмож-

ности линейной обратной связи. Именно, применим для стабилизации

в нуле Е-системы

(Tj = (72, (72 = U

198

Глава 5.

Скользящие режимы высших

порядков

за конечное время

линейную обратную связь с переменными па-

раметрами и =

—kW

= —iti<Ti—А:2<Г2, где для удобства введены векторы

к^ = {ki,k2) и ff = («Ti,«гг); здесь ^ — знак транспонирования.

Общее решение Е-системы дается формулой Коши

W{t) = е

где матрица А и вектор 6 имеют вид

•тА

budr

л=[У.].

'=[?]

Положим

и(0 = -б"^е-'^ I,

где вектор I определяется из равенства ?(»j) = О, т.е.

(То =

!•

-'•^ ЬЬ^е-"^

l = W(0,v)l.

Поскольку Е-система управляема, то граммиан управляемости

W(0,T])

невырожден при любом »; > О, и поэтому / =

W~^(0,T))WO,

ЧТО и по-

зволяет найти управление, решающее задачу в виде "программы"

« = -6'е

т^-м^

W-\0,T,)Wo.

Для нахождения соответствующей обратной связи выразим <го из

равенства

а результат подставим в предыдущую формулу для и. Получим сле-

ду юхцую формулу:

и =

jTg-M w-^iO,r,)e

-tA

1-1^(0,0^^-40,»;) '

которая и определяет искомую обратную связь. Поскольку

W{0,t)W-\Q,r})^l

при t

—>

т;, то коэффициент обратной связи неограниченно возрастг1ет

за конечное время, т.е.

k(t) = -

-tA

l-W{0,t)W-^{0,T))

•ОС,

5.2. Алгоритмы

скольжения

2-го порядка

199

Последнее, конечно, неприемлемо в приложениях. Для явного вы-

ражения параметров Ari(t) и k2(t) через параметры Е-системы нужно

использовать следующие формулы:

6*"^ =

»'-'(».')= [б/.^ tt]- »v'-^

H,ii.

5.2.4. Финитные алгоритмы скольжения 2-го порядка:

релейная обратная связь

Рассмотрим теперь нелинейную обратную связь, которгш также обес-

печивает финитную стабилизацию, но ограничена при любых

«г.

Пусть

скалярная гладкая функция

д{<т)

такова, что д{0) = 0, д' д ограничена,

решение дифференциального уравнения а =

д(<т)

существует при лю-

бом (г(0) и это решение за конечное время попадает в нуль. Например,

такими свойствами обладает функция ^((г) = —dsgner

\(т\р,

0.5 < р <1,

d = const > 0.

Тогда обратную связь, финитно стабилизирующую Е-систему

&1 = <Т2,

<^1

— U,

можно выбрать релейной, например в виде

« = -*sgn^(<ri,<r2),

При достаточно большом коэффициенте к > О кривая (Тг =

9{<''i)

будет кривой скольжения, она достига1ется из любого начального по-

ложения за конечное время, что и гарантирует финитность времени

стабилизации

г)

(рис. 5.19).

Рис.

5.19

200

Глава 5. Скользящие

режимы

высших порядков

5.2.5. Алгоритм скручивания

Исследуем стабилизирующие свойства разрывной обратной связи вида

и = —ki Sgn

<Ti — к2 Sgn

(Т2,

где ibi > ^2 — положительные параметры. Замкнутая система при

этом описывается уравнениями

ffl = (Т2,

= -ki sgn

(Ti

sgn

ег2,

a отвечающие ей траектории, состоящие из отрезков параболы, изо-

бражены на рис. 5.20.

-iki+ki)

ki+k2 *2\ -(fci-Jkj)

Рис.

5.20

Пусть to, ti, t2, ta и t^ — последовательные моменты переключе-

ния управления, а ri = ti

—

to, Т2 = t2 — ti я т.д. — интервалы

времени между переключениями. Соотношения между последователь-

ными значениями переменных «ri,

(Тг

в моменты переключений даются,

очевидно, следую1Щ1ми выражениями: ai = ± (г\/{к\

-\-

Л2) в первом и

третьем квадрантах,

(Тх

= ^а^Ккх

—

^2) — во втором и четвертом.

Поэтому между квадратами (Т2(0) и (Т2((2) имеет место соотношение

'^2(M = ^^'-l(0) = 'e<Ti(0).

Аналогично имеем

a^{t\)

= Kal{t2) = к^а^О).

Пусть i — номер полного оборота фазового вектора вокруг нуля,

тогда последовательные значения переменной

а-2

связаны следующими

соотношениями:

к2(«)1 = «к2(« -1)1 =... = /с*к2(о)|, ,- =

1,2,...,

откуда следует сходимость переходных процессов Е-системы к нулю,

если только к < 1. Докажем, что эта сходимость финитна.