Гордин Р.К. Геометрия. Планиметрия. 7-9 классы
Подождите немного. Документ загружается.


§ 3.1 351
O
A
B
C
E
K
Рис. 522
O
A
A
1
B
B
1
Рис. 523
Отсюда находим, что x = 1. Следовательно,
S
ABND
= (AB + ND) ·
1
2
AD = 10 · 4 = 40.
3.40. Треугольники KOA и KEO (рис. 522) подобны по
двум углам (∠EOK = ∠ACE = ∠OAK). Поэтому
KE
OK
=
OK
AK
.
Отсюда следует, что OK
2
= EK ·AK. С другой стороны, по тео-
реме о касательной и секущей EK ·AK = KB
2
. Следовательно,
OK = KB.
3.41
0
. Проведем окружность через точки A, B и B
1
(рис. 523). Если A
2
— точка пересечения прямой OA с окружно-
стью, отличная от A, то OA
2
· OA = OB
1
· OB. Следовательно,
точки A
1
и A
2
совпадают.
3.42. Пусть окружности пересекаются в точках A и B.
По теореме о произведении отрезков пересекающихся хорд
LP · P N = AP · BP и MP · P K = AP · BP (рис. 524). По-
этому LP ·P N = MP ·P K. Следовательно, точки L, M, N и K
лежат на одной окружности.
3.43
0
. Предположим, что C
1
— вторая точка пересечения
прямой MC с данной окружностью (рис. 525). Из теоремы
P
A
B
K
L
M
N
Рис. 524
A
B
C
C
1
M
Рис. 525
352 9 класс
D
A
B
C
M
Рис. 526
A
B
C
D
M
P
S
S
1
Рис. 527
о касательной и секущей следует, что
MC ·MC
1
= M A · MB, или MC · (M C ± CC
1
) = MC
2
.
Поэтому точки C и C
1
совпадают.
3.44
0
. Пусть M — точка пересечения продолжения биссек-
трисы CD треугольника ABC с описанной около этого тре-
угольника окружностью (рис. 526). Тогда треугольник CBD
подобен треугольнику CMA (по двум углам). Поэтому
CD
AC
=
BC
CM
,
или
CD · (CD + DM) = AC · BC, CD
2
+ CD · DM = AC · BC.
Следовательно,
CD
2
= AC ·BC − CD · DM = AC · BC − AD · BD
(CD·DM =AD·DB по теореме об отрезках пересекающихся хорд).
3.45. Предположим, что искомая окружность S
1
построена
(рис. 527). Пусть P — точка касания двух окружностей, а M —
точка, в которой прямая AB пересекается с общей касательной
к двум окружностям, проведенной через точку P .
Проведем через точку M прямую, пересекающую окруж-
ность S в двух точках C и D. Тогда M D · MC = MP
2
=
= M A ·MB. Следовательно, точки A, B, C и D лежат на одной
окружности (см. задачу 3.41
0
).
Отсюда вытекает следующий способ построения. Пусть
центр данной окружности S не лежит на серединном перпен-
дикуляре к отрезку AB (иначе построение очевидно). Возьмем
на окружности S произвольную точку C и опишем окружность
около треугольника ABC.
§ 3.1 353
M
B
B
1
A
C
D
E
F
S
1
S
2
S
3
Рис. 528
K
M
O
A
L
P
Q
Рис. 529
Пусть D — вторая точка пересечения построенной окружно-
сти с окружностью S, M — точка пересечения прямых CD и AB.
Проведем из точки M касательные M P и MQ к окружности S
(P и Q — точки касания). Тогда описанные окружности тре-
угольников ABP и ABQ — искомые, поскольку MP
2
= M Q
2
=
= M A · MB (см. задачу 3.43
0
).
3.46
0
. Пусть окружности S
1
и S
2
пересекаются в точках A
и B (рис. 528), окружности S
1
и S
3
— в точках C и D, окруж-
ности S
2
и S
3
— в точках E и F . Если M — точка пересечения
отрезков CD и EF , то по теореме об отрезках пересекающихся
хорд CM ·MD = EM · M F . Через точки A и M проведем пря-
мую, вторично пересекающую окружность S
2
а точке B
1
. Тогда
хорды AB
1
и EF окружности S
2
пересекаются в точке M, по-
этому AM ·M B
1
= EM ·MF = CM ·M D. Значит точки A, B
1
,
C и D лежат на одной окружности, а так как через точки A, C
и D проходит единственная окружность S
1
, то точка B
1
лежит
на окружности S
1
. Таким образом, точка B
1
является общей
точкой окружностей S
1
и S
2
, отличной от точки A. Значит, точ-
ка B
1
совпадает с точкой B. Следовательно, хорда AB проходит
через точку пересечения хорд CD и EF .
3.47. В прямоугольном треугольнике APO (рис. 529) от-
резок AM — проекция катета AP на гипотенузу AO, поэто-
му AO·AM = AP
2
. С другой стороны, по теореме о касательной
и секущей AK ·AL = AP
2
. Значит, AO·AM = AK ·AL, следова-
тельно, точки L, K, M , O расположены на одной окружности.
Вписанные в эту окружность углы MKO и MLO опираются на
одну дугу, поэтому они равны.

354 9 класс
C
O
1
O
2
O
3
A
B
D
F
K
L
M
N
P
Q
Рис. 530
3.48.
2rR
R−r
.
Пусть O
1
и O
2
— центры окружностей радиу-
сов r и R соответственно, O
3
— центр третьей окружности, K —
вторая точка пересечения прямой AC с первой окружностью,
P — точка касания двух первых окружностей (рис. 530).
Поскольку эти окружности касаются, то точка P лежит
на прямой O
1
O
2
. Докажем, что точка пересечения прямых
MN и AB также лежит на прямой O
1
O
2
.
Пусть прямая MN пересекает прямую O
1
O
2
в точке C
′
. Если
Q — проекция точки O
1
на O
2
N, то треугольник O
1
MC
′
подобен
треугольнику O
2
QO
1
с коэффициентом
O
1
M
O
2
Q
=
O
1
M
O
2
N − NQ
=
O
1
M
O
2
N − O
1
M
=
r
R − r
.
Поэтому
C
′
O
1
=
r
R − r
· O
1
O
2
=
r
R − r
(R + r) =
r(R + r)
R − r
.
Пусть прямая AB пересекает прямую O
1
O
2
в точке C
′′
. По-
скольку точка A лежит на отрезке O
1
O
3
, а точка B — на O
2
O
3
,
∠O
1
KA = ∠O
1
AK = ∠O
3
AB = ∠O
3
BA = ∠O
2
BF , где F — вто-
рая точка пересечения прямой AB и окружности с центром O
2
.
Поэтому KO
1
k BO
2
. Пусть прямая, проходящая через точ-
ку O
1
параллельно AB, пересекает радиус O
2
B в точке L. Тогда
треугольник O
1
KC
′′
подобен треугольнику O
2
LO
1
с коэффици-
ентом
O
1
K
O
2
L
=
O
1
K
O
2
B − BL
=
O
1
K
O
2
B − O
1
K
=
r
R − r
.
Поэтому
C
′′
O
1
=
r
R − r
· O
1
O
2
=
r
R − r
(R + r) =
r(R + r)
R − r
.
§ 3.1 355
L
K
F
1
F
2
A
B
C
D
M
Рис. 531
A
A
1
A
2
A
3
A
4
B
C
D
E
Рис. 532
Таким образом, C
′
O
1
= C
′′
O
1
. Значит, точки C
′
и C
′′
сов-
падают. Следовательно, прямые M N и AB пересекаются на
прямой O
1
O
2
.
Теперь найдем CD. Для этого сначала заметим, что точ-
ки A, P и B на сторонах треугольника O
1
O
2
O
3
таковы, что
O
1
A = O
1
P , O
2
B = O
2
P , O
3
A = O
3
B. Значит, в этих точках
вписанная окружность треугольника O
1
O
2
O
3
касается его сто-
рон. Поскольку CP — касательная к этой окружности, CD —
касательная к окружности с центром O
3
, а CAB — общая секу-
щая этих окружностей, CD
2
= CA ·CB = CP
2
. Следовательно,
CD = CP = CO
1
+ O
1
P =
r(R + r)
R − r
+ r =
2rR
R − r
.
3.49. Пусть AB и CD — боковые стороны трапеции ABCD
(рис. 531), M — точка пересечения диагоналей AC и BD, K —
точка пересечения диагонали AC с окружностью, построенной
на боковой стороне AB как на диаметре, а L — точка пересе-
чения диагонали BD со второй окружностью. Тогда ∠BKC =
= ∠BLC = 90
◦
. Поэтому четырехугольник BKLC вписанный.
Следовательно, ∠CKL = ∠CBL = ∠ADB и
∠AKL = 180
◦
− ∠CKL = 180
◦
− ∠ADL.
Поэтому четырехугольник AKLD также вписанный.
Пусть F
1
и F
2
— точки касания первой и второй окружно-
стей с касательными, проведенными из точки M. Тогда M F
2
1
=
= MK · AM = ML · MD = MF
2
2
. Следовательно, MF
1
= MF
2
.
3.50.
ac
b
.
Пусть A
1
, A
2
, A
3
, A
4
— основания перпендику-
ляров, опущенных из точки A на прямые BC, DC, DE и BE
соответственно (рис. 532). Докажем, что треугольник AA
1
A
4
356 9 класс
подобен треугольнику AA
2
A
3
. Действительно,
∠A
1
AA
4
= 180
◦
−∠A
1
BA
4
= ∠CBE = 180
◦
−∠CDE = ∠A
2
AA
3
.
Точки A
1
и A
4
лежат на окружности с диаметром AB, а
точки A
2
и A
3
— на окружности с диаметром AD. Поэтому
∠AA
1
A
4
= ∠ABE = ∠ADE = ∠AA
2
A
3
. Из доказанного следует,
что
AA
1
AA
2
=
AA
4
AA
3
. Отсюда находим, что AA
4
= AA
1
·
AA
3
AA
2
=
ac
b
.
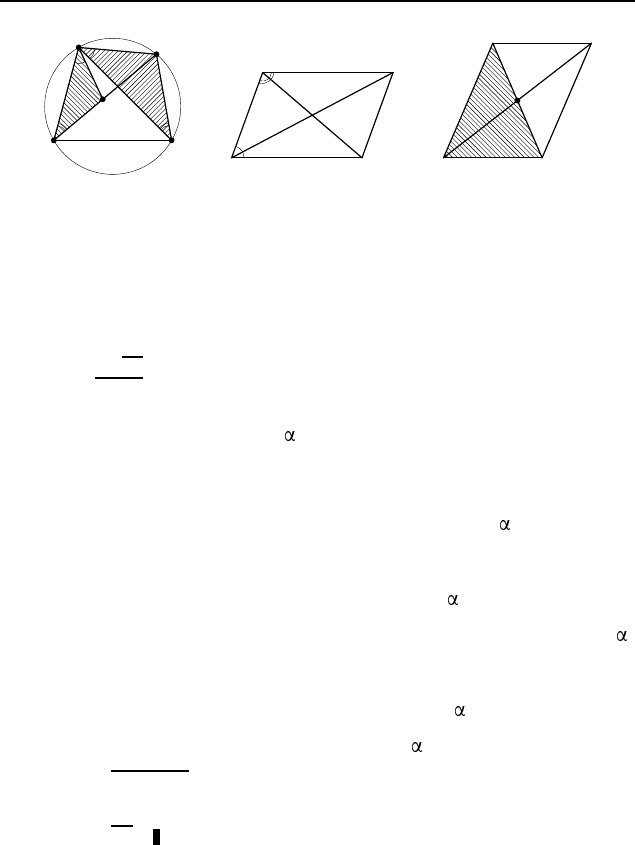
3.51. Пусть четырехугольник ABCD вписан в окружность
(рис. 533). Отложим от луча BA в полуплоскости, содержащей
точку C, луч BP так, что ∠ABP = ∠CBD (P — на AC).
Треугольники ABP и DBC подобны по двум углам. Поэто-
му
AB
AP
=
BD
CD
, или AB · CD = AP · BD. Треугольники P BC
и ABD также подобны по двум углам (∠ABD = ∠P BC,
∠BDA = ∠BCP ). Поэтому
BC
P C
=
BD
AD
, или BC ·AD = P C ·BD.
Сложив почленно доказанные равенства, получим, что
AB · CD + BC · AD = AP · BD + BD · P C =
= BD · (AP + P C) = BD · AC.
§ 3.2
3.52. Нет.
3.53. Указание. Примените теорему косинусов.
3.54.
a
√
7
3
.
3.55. Обозначим указанные стороны через a и 2a. Тогда по
теореме косинусов квадрат третьей стороны равен
a
2
+ 4a
2
− 2 · a · 2a ·
1
2
= 3a
2
.
Пусть
— угол данного треугольника, лежащий против сторо-
ны, равной 2a. Тогда по теореме косинусов
cos =
a
2
+ 3a
2
− 4a
2
2 · a · a
√
3
= 0.
Следовательно,
= 90
◦
.
3.56. 2, 4
√
3. Указание. Обозначьте стороны, образующие
угол в 30
◦
, через x и 2x
√
3 и воспользуйтесь теоремой косинусов.
3.57.
3
5
.
3.58. 2
√
19,
√
37. Указание. Рассмотрите треугольники ACD
и BCD.
§ 3.2 357
A
B
C
D
P
Рис. 533
A
B C
D
Рис. 534
M
A
B C
D
Рис. 535
3.59. 2 или 4. Указание. С помощью теоремы косинусов со-
ставьте уравнение относительно искомой стороны.
3.60. Указание. С помощью теоремы косинусов вычисли-
те BC и CD.
3.61.
a
√
13
3
. Указание. Через вершину A проведите прямую,
параллельную MN .
3.62
0
. Обозначим через
угол при вершине A параллело-
грамма ABCD (рис. 534). По теореме косинусов из треугольни-
ков ABD и ABC находим, что
BD
2
= AB
2
+ AD
2
− 2 · AB · AD ·cos
и
AC
2
= AB
2
+ BC
2
− 2 · AB · BC · cos(180
◦
− ) =
= AB
2
+ AD
2
+ 2 · AB · AD ·cos
.
Тогда
BD
2
+ AC
2
= (AB
2
+ AD
2
− 2 · AB ·AD · cos )+
+ (AB
2
+ AD
2
+ 2 · AB ·AD · cos
) = 2 · AB
2
+ 2 · AD
2
.
3.63.
√
4a
2
+ b
2
. Указание. Примените теорему Пифагора и
воспользуйтесь результатом предыдущей задачи.
3.64.
√
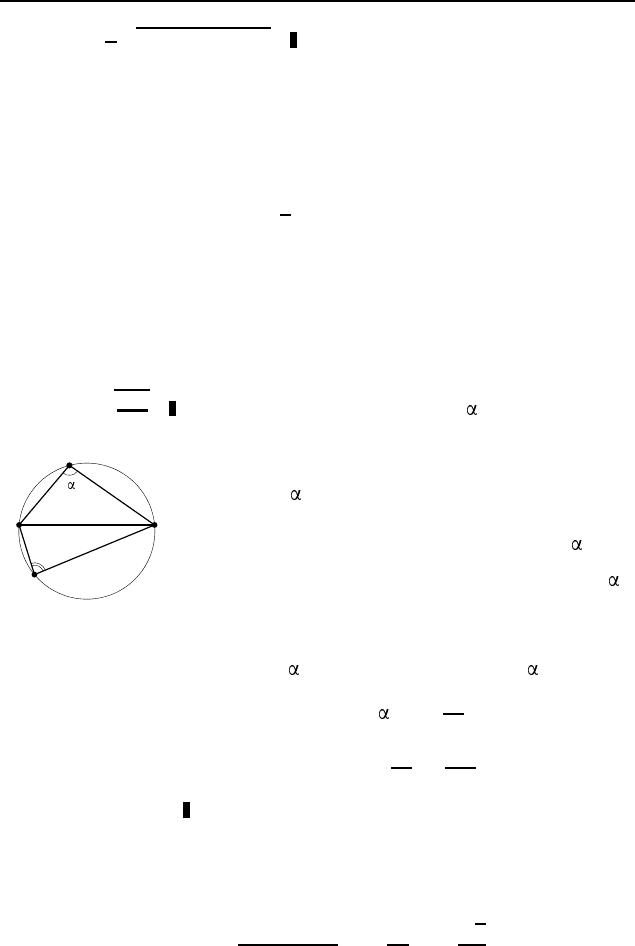
10. Обозначим через x основание BC равнобед-
ренного треугольника ABC (рис. 535). На продолжении меди-
аны BM за точку M отложим отрезок DM, равный BM. То-
гда BADC — параллелограмм. Поэтому
AC
2
+ BD
2
= 2(AB
2
+ BC
2
), или 36 + 16 = 2 · 16 + 2x
2
.
Отсюда находим, что x
2
= 10.
3.65. 6.
358 9 класс
3.66
0
.
1
2
√
2a
2
+ 2b
2
− c
2
. Пусть в треугольнике ABC из-
вестно, что AB = c, BC = a, AC = b; медиана CM = m. На
продолжении медианы CM за точку M отложим отрезок
MD, равный CM. Тогда ACBD — параллелограмм. Поэтому
CD
2
+ AB
2
= 2(AC
2
+ BC
2
), или 4m
2
+ c
2
= 2(a
2
+ b
2
).
Отсюда находим, что m
2
=
1
4
(2a
2
+ 2b
2
− c
2
).
3.67. 9,5.
3.68. 30. Указание. Воспользуйтесь результатом зада-
чи 3.66
0
.
3.69. Указание. Выразите квадрат каждой медианы по фор-
муле, полученной в задаче 3.66
0
, и сложите почленно три по-
лученных равенства.
3.70.
q
299
11
.
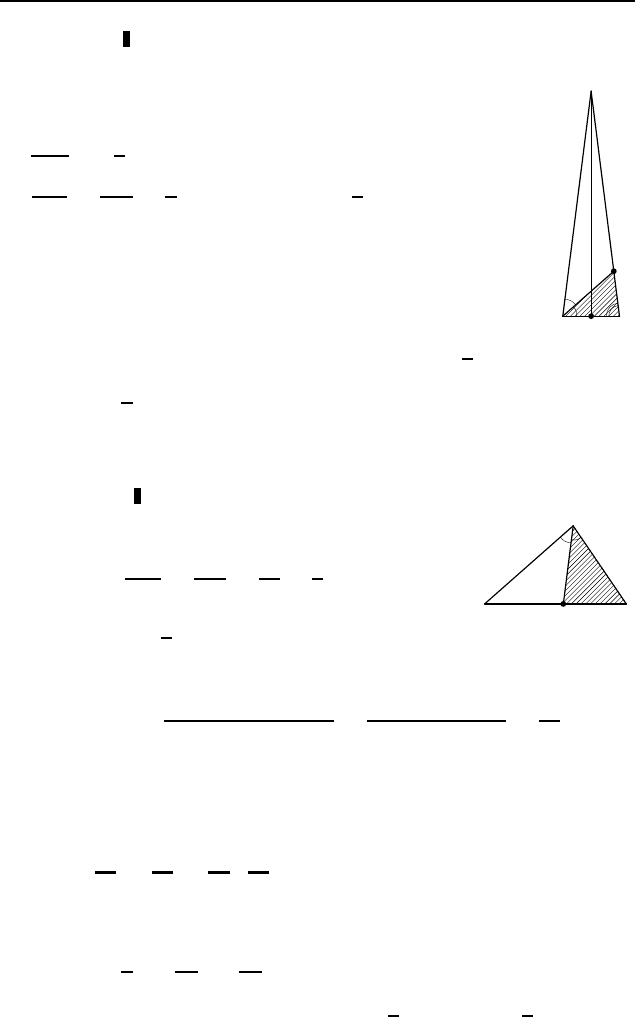
Обозначим у гол ∠ABC = (рис. 536). По-
A
B
C
D
Рис. 536
скольку около четырехугольника ABCD
можно описать окружность, то ∠ADC =
= 180
◦
−
, поэтому
AC
2
= AB
2
+ BC
2
− 2 · AB ·BC ·cos =
= AD
2
+ CD
2
− 2 · AD · CD · cos(180
◦
−
),
или
9 + 16 − 2 · 3 ·4 · cos
= 4 + 25 + 2 · 2 · 5 · cos .
Из этого уравнения находим, что cos
= −
1
11
. Следовательно,
AC
2
= 9 + 16 + 2 ·3 · 4 ·
1
11
=
299
11
.
3.71. Нельзя.
Если бы около данного четырехугольника
можно было описать окружность, то сумма его противолежа-
щих углов была бы равна 180
◦
. По теореме косинусов из тре-
угольника ABC находим, что
cos ∠B =
9 + 16 − 36
2 · 3 · 4
= −
11
24
6= −
√
3
2
.
Поэтому ∠B + ∠D 6= 180
◦
. Следовательно, около четырехуголь-
ника ABCD нельзя описать окружность.
§ 3.2 359
3.72. 6. Пусть BK — биссектриса угла при основании BC
A
B C
K
M
Рис. 537
(рис. 537) равнобедренного треугольника ABC (AB =
= AC = 20, BC = 5), M — середина BC. Из прямо-
угольного треугольника AMC находим, что cos ∠C =
=
MC
AC
=
1
8
. По свойству биссектрисы треугольни-
ка
AK
KC
=
AB
BC
=
4
1
. Поэтому KC =
1
5
AC = 4.
По теореме косинусов из треугольника BKC на-
ходим, что
BK
2
= BC
2
+ KC
2
−2 · BC ·KC · cos ∠C =
= 25 + 16 − 2 · 5 · 4 ·
1
8
= 36.
3.73. 8
√
2. Указание. По теореме косинусов из треугольни-
ка ABC найдите cos ∠B, затем а из треугольника ABM — сто-
рону AM.
3.74. 10.
Пусть AK — биссектриса тре-
A
BC K
Рис. 538
угольника ABC (рис. 538). Тогда
CK
KB
=
AC
AB
=
15
12
=
5
4
.
Поэтому BK =
4
9
BC = 8. По теореме косину-
сов из треугольника ABC находим, что
cos ∠B =
AB
2
+ BC
2
− CA
2
2 · AB · BC
=
144 + 324 − 225
2 · 12 · 18
=
9
16
.
Тогда из треугольника ABK находим, что
AK
2
= BK
2
+ AB
2
−2 ·BK ·AB ·cos ∠B = 144 + 64 −108 = 100.
3.75.
37
40
, −
37
40
, −
5
16
,
5
16
. Указание. Через конец C меньше-
го основания BC трапеции ABCD проведите прямую, парал-
лельную боковой стороне AB, и примените теорему косинусов к
полученному треугольнику.
3.76. 4
√
7, 2
√
13, 2
√
19. Указание. Пусть BD и CE — меди-
аны треугольника ABC. Тогда BM =
2
3
BD, CM =
2
3
CE.
360 9 класс
3.77.
5
2
√
7
. Указание. Пусть M и N — середины сторон BC
и CD параллелограмма ABCD. Найдите стороны треугольни-
ка AMN.
3.78.
√
273. Указание. Пусть окружность, вписанная в тре-
угольник ABC, касается стороны AC в точке K. Обозначь-
те CK = x и с помощью теоремы косинусов составьте уравнение
относительно x.
3.79. 120
◦
. Указание. Через конец B меньшего основа-
ния BC трапеции ABCD проведите прямую, параллельную
диагонали AC. Далее примените теорему косинусов.
3.80.
√
a
2
+ b
2
± ab. Указание. Середины сторон любого че-
тырехугольника являются вершинами параллелограмма.
3.81.
1
2
p
c
2
+ d
2
± cd
√
2.
3.82.
p
a
2
+ b
2
+ ab
√
2. Указание. Если биссектрисы углов B
и C треугольника ABC пересекаются в точке M, то ∠BMC =
= 90
◦
+
1
2
∠A (см. задачу 1.116
0
).
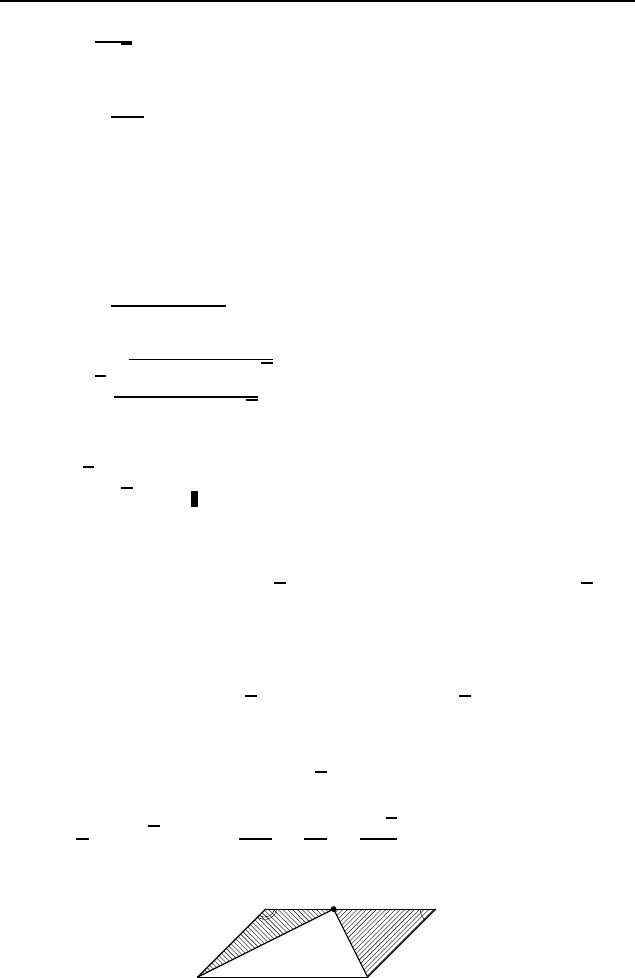
3.83. 2
√
2 : 5. Обозначим BM = 2x, CM = 3x, AB =
= CD = y (рис. 539). Из треугольников ABM и CDM по
теореме косинусов находим, что
AM
2
= 4x
2
+ y
2
+ 2xy
√
2 и DM
2
= 9x
2
+ y
2
− 3xy
√
2.
По теореме Пифагора из прямоугольного треугольника AMD
находим, что AM
2
+ MD
2
= AD
2
, или
(4x
2
+ y
2
+ 2xy
√
2) + (9x
2
+ y
2
− 3xy
√
2) = 25x
2
,
или
12x
2
+ xy
√
2 − 2y
2
= 0,
откуда
y
x
= 2
√
2. Тогда
AB
BC
=
y
5x
=
2
√
2
5
.
A
B C
D
M
Рис. 539
