Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

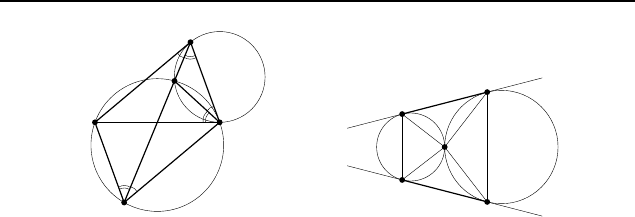
§ 2.10 341

Рис. 495

Рис. 496

Поэтому CD k AB. С другой стороны,

∠DAC = ∠MAC = ∠MCB = ∠BDM = ∠BDA.

Поэтому BD k AC. Следовательно, ABDC — параллелограмм.

Его диагональ AD делит вторую диагональ BC пополам.

2.667. Указание. Биссектрисы углов A и B четырехуголь-

ника ABCD пересекаются в середине дуги AB, а биссектрисы

углов D и C — в середине дуги CD (рис. 496).

9 класс

§ 3.1

3.1. 7,5. 3.2. 8, 8, 8. 3.3. 12 или 3

√

2. 3.4. 3

√

6 : 8. 3.5. 12, 6.

3.6.

ac+bd

. 3.7

. R

− d

. 3.8

. d

− R

3.9. 0,2.

Точка B расположена между точками A и C

(рис. 497). Предположим, что точка D расположена между точ-

ками A и E. Тогда AB ·AC = AD ·AE, или 14·7 = 10·(10+DE)

(см. задачу 3.8

). Отсюда находим, что DE = −0,2, что невоз-

можно. Поэтому точка E расположена между A и D. Тогда

AB ·AC = AD ·AE, или 14 ·7 = 10 ·(10 −DE). Отсюда находим,

что DE = 0,2.

3.10. 6.

3.11.

√

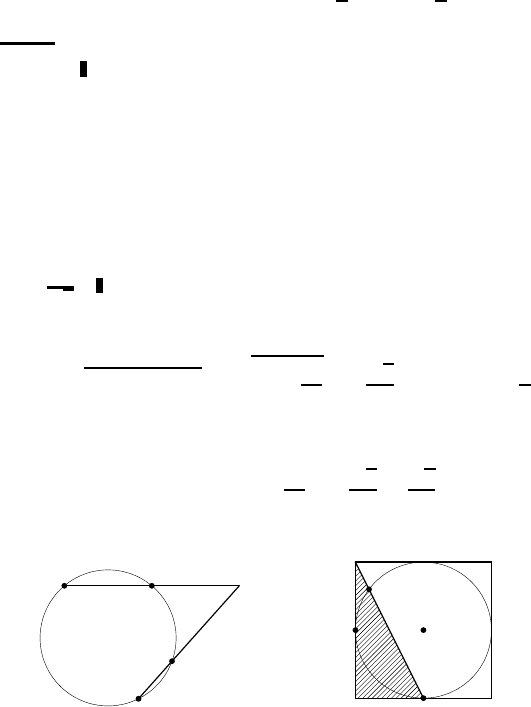
Пусть P E — искомая хорда, M — точка касания

окружности со стороной AD (рис. 498). Тогда

AE =

+ DE

= a

√

, AM =

По теореме о касательной и секущей

= AE · AP, или

= a

√

· a

√

− P E.

Рис. 497

A B

CD E

Рис. 498

§ 3.1 343

Рис. 499

Рис. 500

Рис. 501

Из этого уравнения находим, что P E =

√

3.12.

2ar

√

3.13. 13.

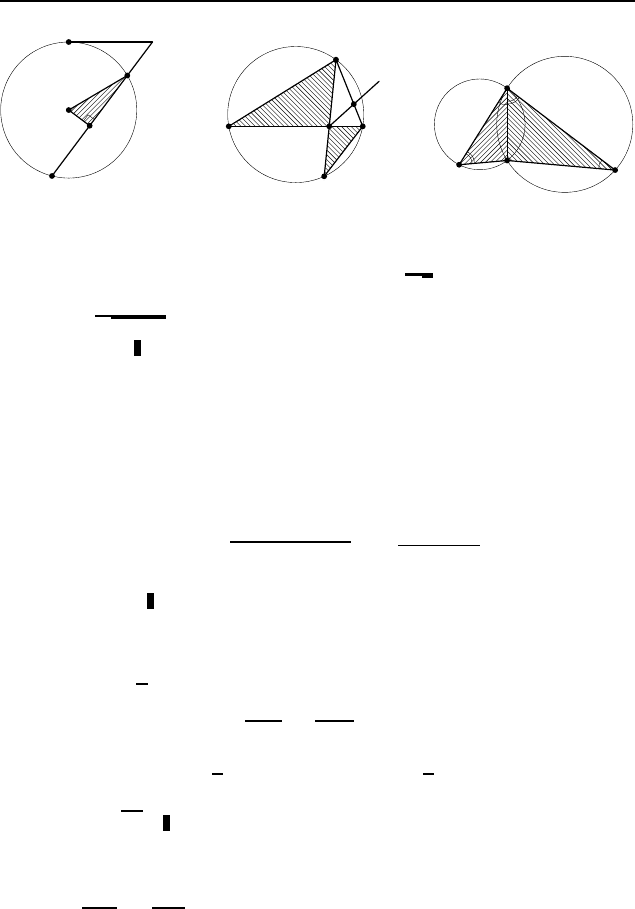
Пусть секущая пересекает окружность в точ-

ках B и C, а M — точка касания (рис. 499). Тогда AM = 16,

AC = 32, BC = 32 − BA. По теореме о касательной и секу-

щей AM

= AC ·AB, или 16

= 32(32 − BC). Отсюда находим,

что BC = 24. Пусть K — проекция центра O данной окруж-

ности на хорду BC. Из прямоугольного треугольника OKB по

теореме Пифагора находим, что

R = OB =

+ BK

√

25 + 144 = 13.

3.17. 1, 2.

Треугольники BMC и DMA (рис. 500) подоб-

ны (∠MCB = ∠DCB = ∠DAB = ∠DAM). Поскольку площади

этих треугольников относятся как 1 : 4, то коэффициент по-

добия равен

, и DM = 2BM. Так как MK — биссектриса

треугольника BMD, то

= 2. Следовательно,

DK = 2 ·

BD = 2, BK =

BD = 1.

3.18

√

ab. По теореме об у гле между касательной и хор-

дой ∠BAC = ∠BDA и ∠BAD = ∠BCA (рис. 501), поэтому

треугольники ABC и DBA подобны по двум углам. Следова-

тельно,

, откуда находим, что AB

= BC · BD = ab.

3.19. 4.

3.20

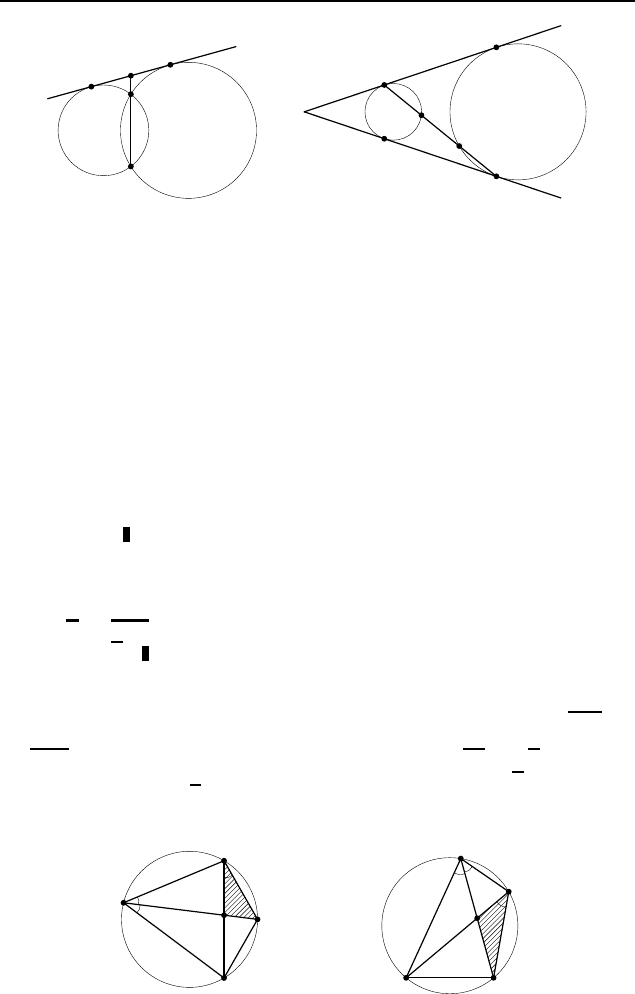
. Пусть A и B — точки пересечения окружностей

(рис. 502), MN — общая касательная (M и N — точки ка-

сания), K — точка пересечения прямых AB и MN (A между K

344 9 класс

Рис. 502

Рис. 503

и B). Тогда MK

= KB ·KA и NK

= KB ·KA. Следовательно,

MK = NK.

3.21. Пусть P и Q — точки пересечения прямой K

со-

ответственно с первой и второй окружностями, отличные от

точек K

и L

(рис. 503). По теореме о касательной и секущей

Q · K

= K

и L

P · K

= K

Поскольку K

= K

, то K

Q = L

P . Следовательно,

P = L

3.22. 2.

Поскольку ∠KBC = ∠DBC = ∠DAC = ∠BAC

(рис. 504), то треугольник KBC подобен треугольнику BAC

(по двум у глам). Поэтому KC : BC = BC : AC. Пусть KC = x.

Тогда

x+6

. Из этого уравнения находим, что x = 2.

3.23.

√

2. Пусть M — середина BC (рис. 505). Посколь-

ку ∠ADC = ∠ABC = ∠CBD, то треугольник DCM подобен

треугольнику BCD (по двум у глам). Следовательно,

. Обозначим BM = CM = x. Тогда

. Отсюда

находим, что x

. Следовательно, BC = 2x =

√

Рис. 504

Рис. 505

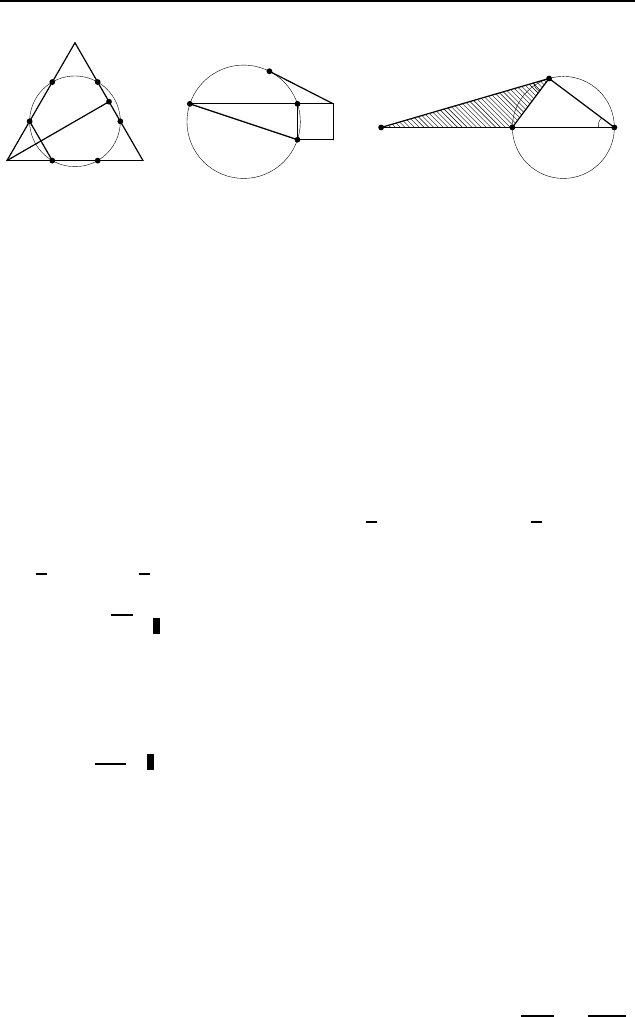
§ 3.1 345

A B

Рис. 506

Рис. 507

Рис. 508

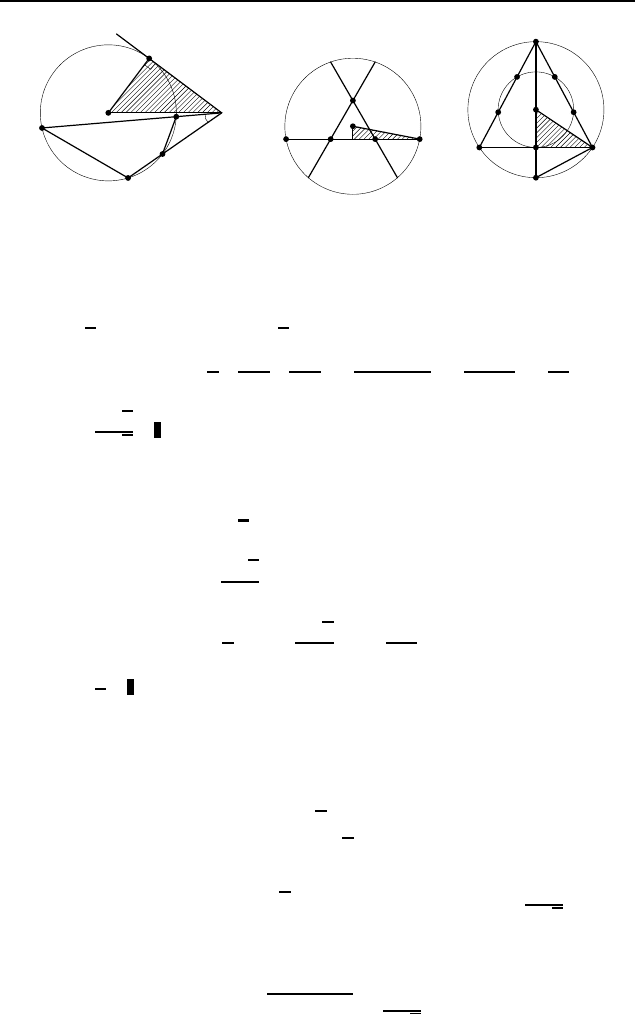
3.24. Первый способ. Пусть A и B, C и D, E и F — точки

пересечения окружности со сторонами P Q, QR, RP треуголь-

ника P QR (рис. 506). Рассмотрим медиану P S. Она проходит

через середины параллельных хорд F A и DC и поэтому перпен-

дикулярна им. Следовательно, P S является высотой треуголь-

ника P QR, а значит, P Q = P R. Аналогично, P Q = QR.

Второй способ. Пусть A и B, C и D, E и F — точки пересече-

ния окружности со сторонами P Q, QR и RP треугольника QP R

(см. рис. 506). Рассмотрим секущие P B и P E. Поскольку

P A · P B = P F · P E, P A =

P Q, P F =

P R,

то

P Q

P R

. Следовательно, P Q = P R. Аналогично,

P Q = QR.

3.25.

√

10. Пусть AD — хорда окружности, луч BA пе-

ресекает окружность в точке M , отличной от A (рис. 507). То-

гда BM · AB = BK

. Отсюда находим, что AM = 3. Посколь-

ку ∠DAM = 90

◦

, то DM — диаметр окружности. Следователь-

но, DM

= AD

+ AM

= 1 + 9 = 10.

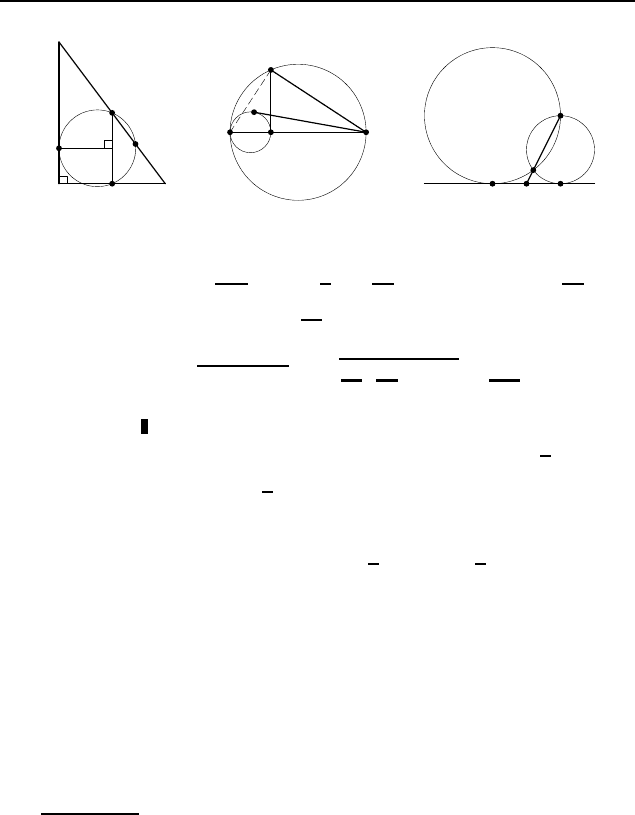
3.26.

120

Пусть AB = 10, BC = 8 и AC = 6 — стороны

данного треугольника ABC (рис. 508). Поскольку AB

= BC

+AC

, треугольник ABC прямоугольный, причем ∠ACB = 90

◦

поэтому AB — диаметр окружности, описанной около тре-

угольника ABC. Если касательная, проведенная к окружно-

сти через точку C (вершина наибольшего у гла), пересекает

продолжение наибольшей стороны AB в точке M, то по тео-

реме о касательной и секущей MC

= MA · MB. Обозна-

чим MA = x. Тогда MC

= x(x + 10). С другой стороны, из

подобия треугольников AMC и CMB следует, что

346 9 класс

Рис. 509

Рис. 510

Рис. 511

откуда MC = M A ·

= x ·

. Из уравнения

= x(x + 10) находим, что x =

. Следовательно,

MC =

x(x + 10) =



+ 10



120

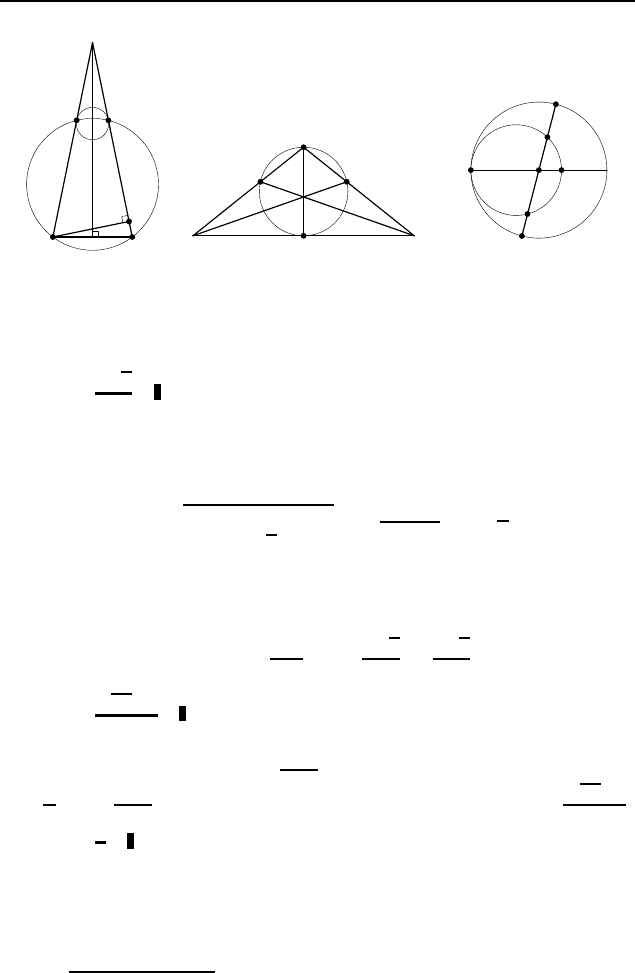
3.27. 1,1.

Пусть M и N — середины AC и AB соответ-

ственно, K — точка касания (рис. 509). Тогда M N =

BC = 2,

CK = CB − KB = CB −

MN = 4 − 1 = 3. Пусть T — вторая

точка пересечения окружности с гипотенузой AC. Тогда

CT · CM = CK

, или



+ MT



= 9.

Отсюда находим, что MT = 1,1.

3.28. В прямоугольном треугольнике ADC (рис. 510) от-

резок BD — высота, проведенная из вершины прямого угла.

Поэтому DC

= BC ·AC. С другой стороны, по теореме о каса-

тельной и секущей CK

= BC ·AC. Следовательно, CD = CK.

3.29

. Пусть A и B — данные точки (рис. 511), M — точ-

ка пересечения прямой AB с данной прямой, K — искомая

точка касания. По теореме о касательной и секущей MK =

√

MB · MA.

Отсюда вытекает следующий способ построения. Строим

отрезок, равный среднему геометрическому известных отрез-

ков MB и MA, и откладываем его по разные стороны от

точки M на данной прямой. Остается построить окружности,

проходящие через точки A, B и каждую из построенных точек.

Если точки A и B расположены по одну сторону от дан-

ной прямой и удалены от нее на разные расстояния, то задача

§ 3.1 347

D E

Рис. 512

B CD

Рис. 513

Рис. 514

имеет два решения, если на равные — одно решение. В осталь-

ных случаях решений нет.

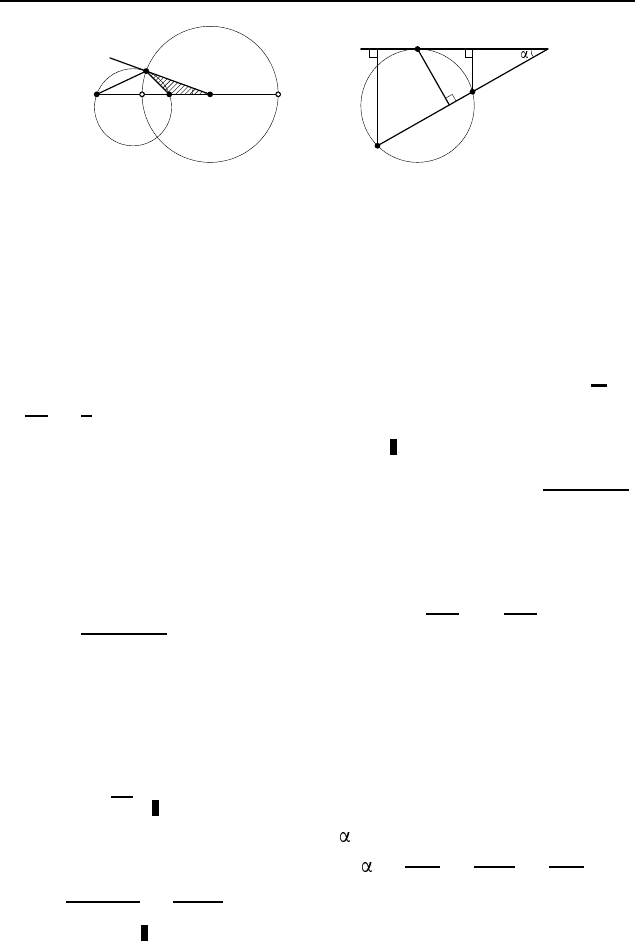
3.30.

√

Из теоремы о касательной и секущей следу-

ет, что BA · BD = BE · BC (рис. 512). Поскольку BD = BE,

то AB = BC, т. е. треугольник ABC равнобедренный. Пусть

h — высота треугольника ABC, опущенная из вершины B. Тогда

h =

−





√

25 − 1 = 2

√

Если AP — искомая высота треугольника ABC, то AC · h =

= BC · AP . Следовательно,

AP = AC ·

= 2 ·

√

3.31.

√

17−1

Пусть BC = x (рис. 513). По свойству бис-

сектрисы треугольника CE : AE = BC : AB = x : 1. От-

сюда находим, что CE =

1+x

. Поскольку CD

= CE · AC,

то





1+x

. Из этого уравнения находим, что x =

√

17−1

3.32.

Пусть M — точка касания окружностей

(рис. 514), r и R (r < R) — их радиусы, Q — центр боль-

шей из окружностей. Обозначим: AB = 3x, BC = 7x, CD = 2x.

Тогда

R =

AB + BC + CD

= 6x, BQ = AQ − AB = R − 3x = 3x,

QC = R − 2x = 4x, M Q = R = 6x, QP = 2r −M Q = 2r − 6x

348 9 класс

Рис. 515

Рис. 516

(где MP — диаметр меньшей окружности). По теореме об от-

резках пересекающихся хорд

BQ · QC = MQ · QP, или 3x · 4x = 6x · (2r − 6x).

Из этого уравнения находим, что r = 4x. Следовательно,

3.33. Окружность без двух точек.

Если M — одна из то-

чек касания, то CM

= CA·CB. Следовательно, точка M лежит

на окружности с центром C и радиусом, равным

√

CA · CB.

Рассмотрим теперь любую точку P этой окружности, не ле-

жащую на прямой AC (рис. 515). Опишем окружность око-

ло треугольника AP B. Тогда треугольники AP C и P BC по-

добны, так как угол C у них общий, и

P C

, так как

P C =

√

AC · BC. Поэтому ∠CP B = ∠P AC = ∠P AB.

Если касательная, проведенная к описанной окружности

треугольника AP B в точке P , пересекает луч BC в точке C

то ∠C

P B = ∠P AB = ∠CP B. Поэтому точки C

и C сов-

падают. Следовательно, CP — касательная к окружности,

проходящей через точки A и B.

3.34.

√

ab. Обозначим через K точку пересечения пря-

мой AB с указанной касательной,

— угол между ними, x — ис-

комый отрезок (рис. 516). Тогда sin

. По-

этому

AK·BK

. Поскольку AK ·BK = MK

, то x

= ab.

3.35. 1,6.

Проведем из точки A касательную к данной

окружности (рис. 517). Пусть M — точка касания, O — центр

окружности. Из прямоугольного треугольника OMA находим,

что AM

= AO

− OM

= 25 −9 = 16.

§ 3.1 349

O A

Рис. 517

Рис. 518

Рис. 519

Тогда AK · AC = AL · AB = AM

= 16. Поэтому

AKL

AK · AL sin 30

◦

AK · AL =

AC · AB

ABC

= 1,6.

3.36.

√

. Из теоремы о произведениях отрезков пересе-

кающихся хорд следует, что все три хорды равны между собой.

Поэтому точки пересечения хорд — вершины правильного тре-

угольника со стороной

(рис. 518). Центр этого треугольника

совпадает с центром данной окружности. Расстояние от него до

каждой хорды равно

√

. Поэтому квадрат искомого радиуса

равен







√



3.37.

Пусть меньшая окружность с центром O касается

стороны AB треугольника ABC в точке P , пересекает сторо-

ну BC в точках M и N , а сторону AC — в точках K и L,

и BM = MN = NC = a, AK = KL = LC = b (рис. 519).

Поскольку CM · CN = CK · CL, то a = b, а так как P B

= BN · BM, то P B = AP = a

√

2. Из прямоугольного треуголь-

ника CP B находим, что CP = a

√

Пусть CF — диаметр большей окружности, R — радиус. То-

гда CP ·CF = BC

, или a

√

7 ·2R = 9a

, откуда R =

√

. Тогда

радиус r меньшей окружности находим из прямоугольного тре-

угольника OP B:

r =

− 2a

√

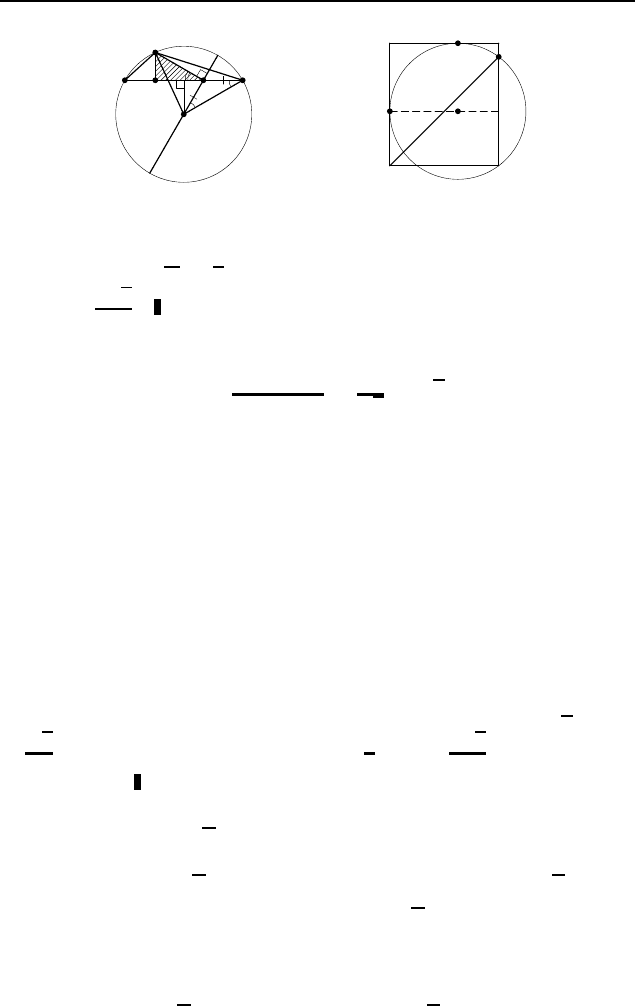
350 9 класс

Рис. 520

Рис. 521

Следовательно,

3.38.

√

Пусть O — центр окружности, R — ее радиус

(рис. 520). Тогда

R =

AB/2

cos ∠OBA

√

Поскольку (R −OD)(R + OD) = AD · DB, то

= R

− AD · DB = 3 − 1 · 2 = 1.

Поэтому OD = 1. Следовательно, треугольник ODC — прямо-

угольный (OC

= OD

+ CD

) и ∠CDO = 90

◦

. Тогда

∠CDA = ∠CDO −∠ADO =

= 90

◦

− (∠DBO + ∠DOB) = 90

◦

− 60

◦

= 30

◦

Пусть CM — высота треугольника ACB. Тогда CM =

CD =

√

. Следовательно, S

ABC

= AB ·

CM =

√

3.39. 40.

Пусть DN = x, P , Q — точки касания окружно-

сти со сторонами AD и AB (рис. 521). По теореме о касательной

и секущей P D = 3

√

x. Тогда

AP = 8 − 3

√

x = AQ, QB = 9 −AQ = 1 + 3

√

NC = 2QB = 2 + 6

√

Поскольку N C + N D = 9, то

2 + 6

√

x + x = 9, или x + 6

√

x − 7 = 0.