Гордин Р.К. Геометрия. Планиметрия. 7-9 классы
Подождите немного. Документ загружается.

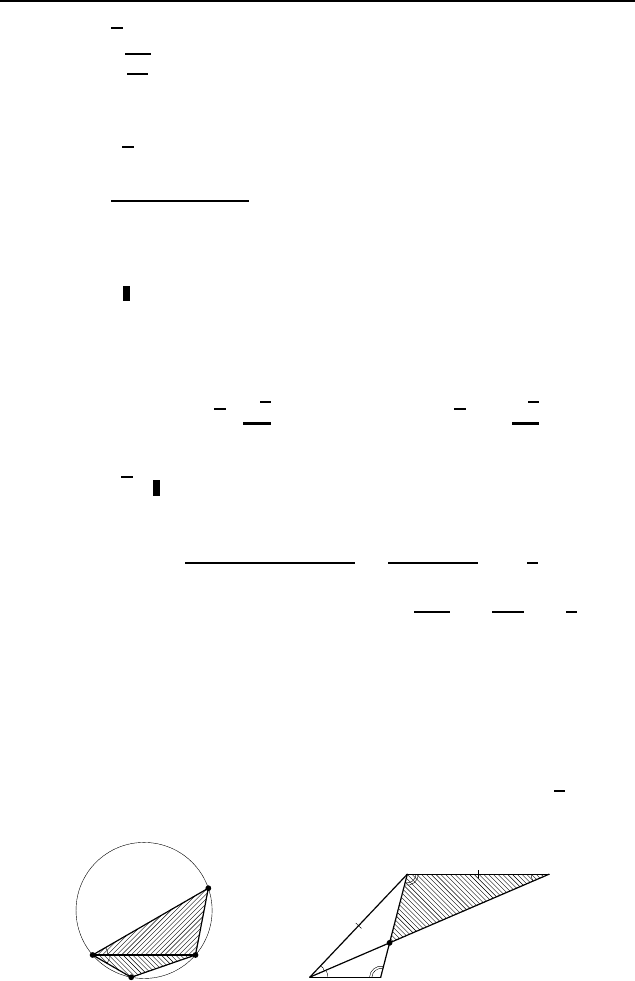
§ 3.2 361
3.84.
√
7. Указание. BD — высота треугольника ABC.
3.85. 2
q
29
5
. Указание. Пусть окружность, вписанная в дан-
ный треугольник ABC (∠C = 90
◦
), касается катета AC в точ-
ке K. Тогда AM = AK = AC − r, где r — радиус окружности.
3.86. a
√
3. Указание. Докажите, что AKM , BLK и CML —
равные прямоугольные треугольники.
3.87.
√
a
2
+ b
2
± 2kab. Указание. Треугольник ABC подо-
бен треугольнику DBE с коэффициентом |cos ∠B| (см. зада-
чу 2.548
0
).
3.88. 4.
Пусть BD = x — искомая хорда (рис. 540). По-
скольку BD — биссектриса угла ABC, то AD = DC. Выра-
зив эти отрезки по теореме косинусов из треугольников ABD
и CBD соответственно, получим уравнение
3 + x
2
− 2x
√
3 ·
√
3
2
= 27 + x
2
− 2 · 3
√
3 · x ·
√
3
2
,
откуда x = 4.
3.89. 2
√
6. По теореме косинусов из треугольника ABC
(рис. 541) находим
cos ∠C =
AC
2
+ BC
2
− AB
2
2 · AC ·BC
=
4 + 9 − 16
2 · 2 · 3
= −
1
4
.
По свойству биссектрисы треугольника
BK
KC
=
AB
AC
=
4
2
= 2.
Поэтому BK = 2. Поскольку ∠AMB = ∠CAM = ∠MAB, то
треугольник ABM равнобедренный, BM = AB = 4. Кроме то-
го, ∠KBM = ∠KCA = ∠C. Следовательно,
KM
2
= BK
2
+ BM
2
− 2 · BK · BM · cos ∠KBM =
= 4 + 16 −2 ·2 · 4 ·
−
1
4
= 24.
A
B
C
D
Рис. 540
A
B
C
K
M
Рис. 541
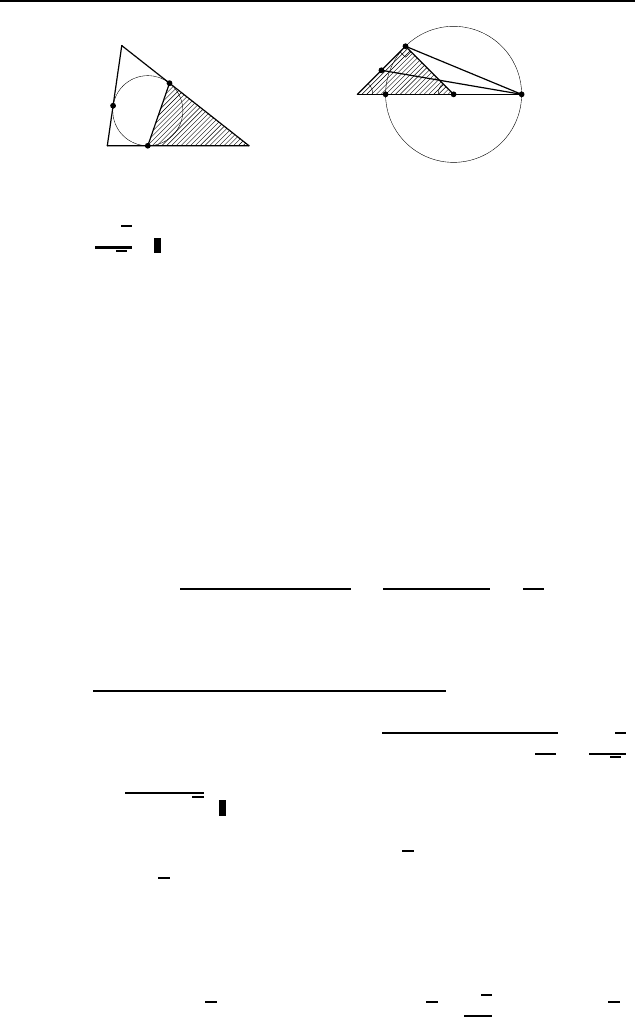
362 9 класс
A
B
C
D
M
N
Рис. 542
C O
K
A
B
M
Рис. 543
3.90.
5
√
3
√
7
. Обозначим BM = BD = x (рис. 542). Тогда
AB = BM + AM = BM + AN = x + 2,
BC = BD + CD = BD + CN = x + 3.
По теореме косинусов
AB
2
= AC
2
+ BC
2
− 2 · AC · BC · cos ∠C,
(x + 2)
2
= 25 + (x + 3)
2
− 5(x + 3).
Из этого уравнения находим, что x = 5. Тогда AB = 7, BC =
= 8. Еще раз применяя теорему косинусов к треугольнику ABC,
находим
cos ∠B =
AB
2
+ BC
2
− AC
2
2 · AB ·BC
=
7
2
+ 8
2
− 5
2
2 · 7 · 8
=
11
14
.
Искомый отрезок M D находим по теореме косинусов из равно-
бедренного треугольника M BD:
MD =
p
BM
2
+ BD
2
− 2 · BM · BD · cos ∠B =
=
q
25 + 25 − 2 · 5 ·
11
14
=
5
√
3
√
7
.
3.91. 2
p
9 + 6
√
2. Пусть O — центр окружности (рис. 543).
Тогда ∠BOC = 2∠BAO = 45
◦
. Из прямоугольного треугольни-
ка OBC находим, что BC = 4, OC = 4
√
2. Поэтому AC = AO +
+ OC = 4 + 4
√
2. Медиану AM находим по теореме косинусов
из треугольника AMC:
AM
2
= AC
2
+ CM
2
− 2 · AC · CM · cos 45
◦
=
= (4 + 4
√
2)
2
+ 4 − 2 · 2 · (4 + 4
√
2) ·
√
2
2
= 4(9 + 6
√
2).

§ 3.2 363
O
x
y
2x
2y
A
B C
K
M
а)
O
A
B C
K
M
N
б )
Рис. 544
3.92. Первый с пособ. Пусть BK и CM — медианы треуголь-
ника ABC, O — их точка пересечения и AC > AB (рис. 544, а).
Обозначим OM = x, OK = y. Тогда OC = 2x, OB = 2y. По
теореме косинусов из треугольников MOB и KOC находим:
BM
2
= x
2
+ 4y
2
− 4xy · cos ∠MOB,
CK
2
= 4x
2
+ y
2
− 4xy · cos ∠KOC.
Поскольку BM =
1
2
AB, KC =
1
2
AC, то
BM
2
< KC
2
, или x
2
+ 4y
2
< 4x
2
+ y
2
(∠MOB = ∠KOC).
Отсюда следует, что x > y. Поэтому CM = 3x > 3y = BK.
Второй спос о б . Пусть BK и CM — медианы треугольни-
ка ABC, O — их точка пересечения и AC > AB (рис. 544, б ).
Проведем медиану AN. В треугольниках AN B и ANC сторо-
на AN общая, BN = CN, а AB < AC, поэтому ∠ANB <
< ∠ANC. В треугольниках ONB и ONC сторона ON общая,
BN = CN, а ∠ON B < ∠ONC, поэтому OB < OC. Следова-
тельно, BK =
3
2
OB <
3
2
OC = CM .
3.93.
2
√
bcp(p−a)
b+c
, где p — полупериметр треугольника. Ука-
зание. Пусть AD — биссектриса треугольника ABC. Найди-
те BD, выразите косинус угла ABC по теореме косинусов из
треугольников ABC и ABD и приравняйте полученные выра-
жения. (Или воспользуйтесь формулой для биссектрисы тре-
угольника (см. задачу 3.44
0
): AD
2
= AB · AC − BD · CD.)
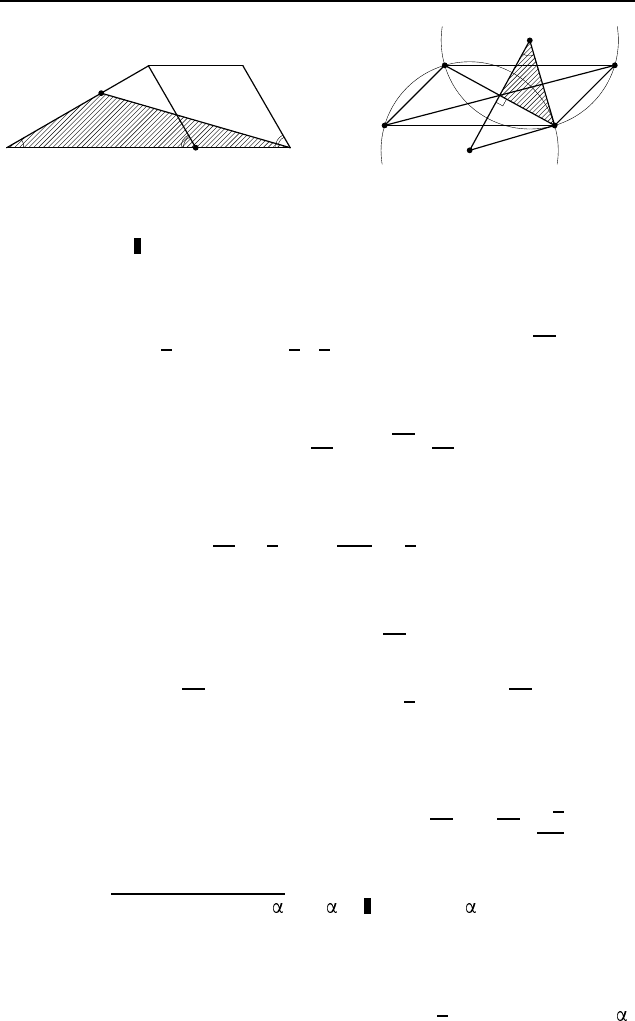
364 9 класс
A
B C
D
K
P
Рис. 545
O
1
O
2
A
B
C
D
Рис. 546
3.94. 13.
Поскольку S
ABD
= 3S
BCD
, то указанная прямая
пересекает отрезок AB (рис. 545). Пусть K — точка пересечения.
Тогда
S
AKD
=
1
2
· S
ABCD
=
1
2
·
1
2
· (AD + BC)h = h
√
39,
где h — высота трапеции ABCD. С другой стороны,
S
AKD
= AD ·
h
1
2
= 3
√
39 ·
h
1
2
,
где h
1
— высота треугольника AKD. Поэтому
h
1
h
=
2
3
и
AK
AB
=
2
3
.
Проведем через вершину B пря мую, параллельную сто-
роне CD, до пересечения с основанием AD в точке P . То-
гда AP = AD −DP = AD − BC = 2
√
39.
Из прямоугольного треугольника ABP находим, что AB =
= AP cos 30
◦
= 3
√
13. Поэтому AK = 2 ·
1
3
AB = 2
√
13.
По теореме косинусов из треугольника AKD находим
DK
2
= AK
2
+ AD
2
− 2 · AK ·AD · cos 30
◦
=
= 4 ·13 + 9 ·39 − 2 ·2
√
13 · 3
√
39 ·
√
3
2
= 169.
Следовательно, DK = 13.
3.95.
√
a
2
+ b
2
+ 2ab cos
|ctg |. Пусть — тупой угол
и O
1
, O
2
— центры окружностей (рис. 546). Поскольку треуголь-
ники BCD и DAB равны, то радиусы окружностей также рав-
ны. Отрезки O
1
O
2
и BD взаимно перпендикулярны и O
1
O
2
де-
лится диагональю BD пополам, ∠DO
1
O
2
=
1
2
∠BO
1
D = 180
◦
−
.
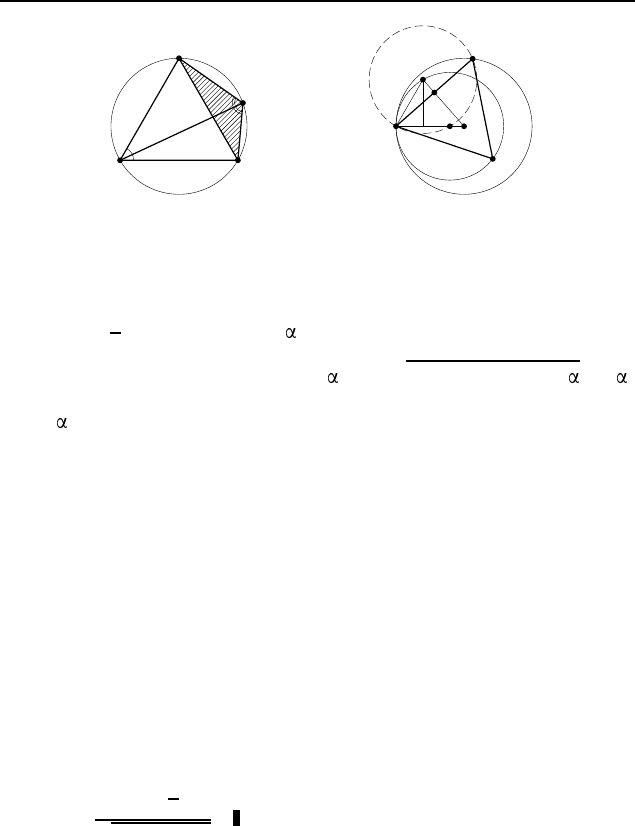
§ 3.2 365
A
B
C
M
Рис. 547
O
M
P
Q
1
Q
A
B
C
S
Рис. 548
Поэтому
O
1
O
2
= 2 ·
1
2
· BD ctg(180
◦
−
) =
= −BD ctg
= −
p
a
2
+ b
2
+ 2ab cos ctg .
Если
— острый угол, решение аналогично.
3.96. Пусть M — произвольная точка окружности, описан-
ной около равностороннего треугольника ABC, лежащая на ду-
ге AB, не содержащей точки C (рис. 547). Обозначим AM = x,
CM = z, BM = y, AB = BC = AC = a. Воспользуемся из-
вестным равенством z = x + y (см. задачу 2.369). Посколь-
ку ∠AMC = ∠BM C = 60
◦
, ∠AMB = 120
◦
, то по теореме
косинусов из треугольника AMB находим, что
x
2
+ y
2
+ xy = a
2
, или x
2
+ y(x + y) = a
2
.
Поскольку x + y = z, то x
2
+ yz = a
2
.
По теореме косинусов из треугольника CMB находим,
что z
2
+y
2
−zy = a
2
. Подставив вместо zy в это равенство a
2
−x
2
,
получим z
2
+ y
2
+ x
2
= 2a
2
.
3.97.
rR
√
3
√
r
2
−rR+R
2
. Пусть окружности радиусов R и r с
центрами соответственно O и Q касаются внутренним образом
в точке A (рис. 548), точка B лежит на первой окружности, точ-
ка C — на второй, причем треугольник ABC — равносторонний.
Пусть при повороте на 60
◦
с центром A, переводящем точку C
в точку B, вторая окружность переходит в окружность S с цен-
тром Q
1
. Тогда AB — общая хорда окружности S и первой
исходной окружности с центром O. Если M — середина этой
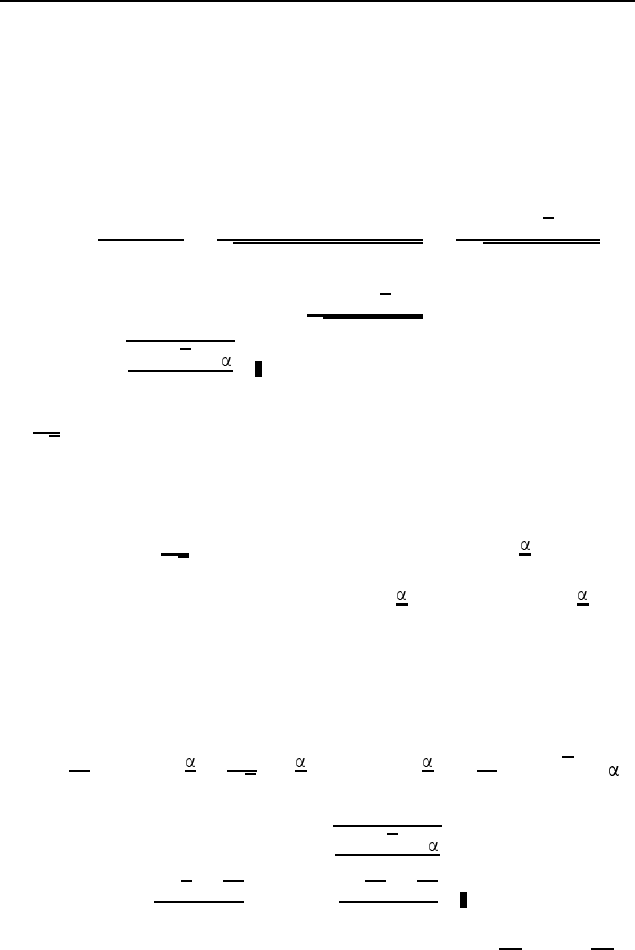
366 9 класс
хорды, то AM — высота треугольника OAQ
1
со сторонами AO =
= R и AQ
1
= r и углом 60
◦
между ними. Пусть Q
1
P — другая
высота этого треугольника. Тогда из прямоугольного треуголь-
ника AP Q
1
находим, что Q
1
P = AQ
1
sin 60
◦
. Отрезок AM равен
удвоенной площади треугольника OAQ
1
, деленной на его осно-
вание OQ
1
, т. е.
AM =
AO · Q
1
P
OQ
1
=
AO · AQ
1
sin 60
◦
√
r
2
+ R
2
− 2rR cos 60
◦
=
rR
√
3
2
√
r
2
− rR + R
2
.
Следовательно, AB = 2AM =
rR
√
3
√
r
2
−rR+R
2
.
3.98. a
r
4+2
√
3 sin
3
.
Пусть P и Q — центры указанных
равносторонних треугольников (рис. 549). Тогда BQ = DP =
=
a
√
3
и BQ k DP . Поэтому отрезок P Q пересекает диаго-
наль BD ромба в ее середине O и делится точкой O пополам.
В треугольнике OBQ
BQ =
a
√
3
, BO = AB sin ∠BAO = a sin
2
,
∠OBQ = ∠OBC + ∠QBC =
90
◦
−
2
+ 30
◦
= 120
◦
−
2
.
По теореме косинусов находим
OQ
2
= BQ
2
+ BO
2
− 2 · BQ · BO · cos ∠OBQ =
=
a
2
3
+ a
2
sin
2
2
−
2a
2
√
3
sin
2
cos
120
◦
−
2
=
a
2
6
(2 +
√
3 sin ).
Следовательно, P Q = 2QO = a
r
4+2
√
3 sin
3
.
3.99. arcsin
7
√
3−
√
77
28
= arccos
7
√
11+
√
21
28
.
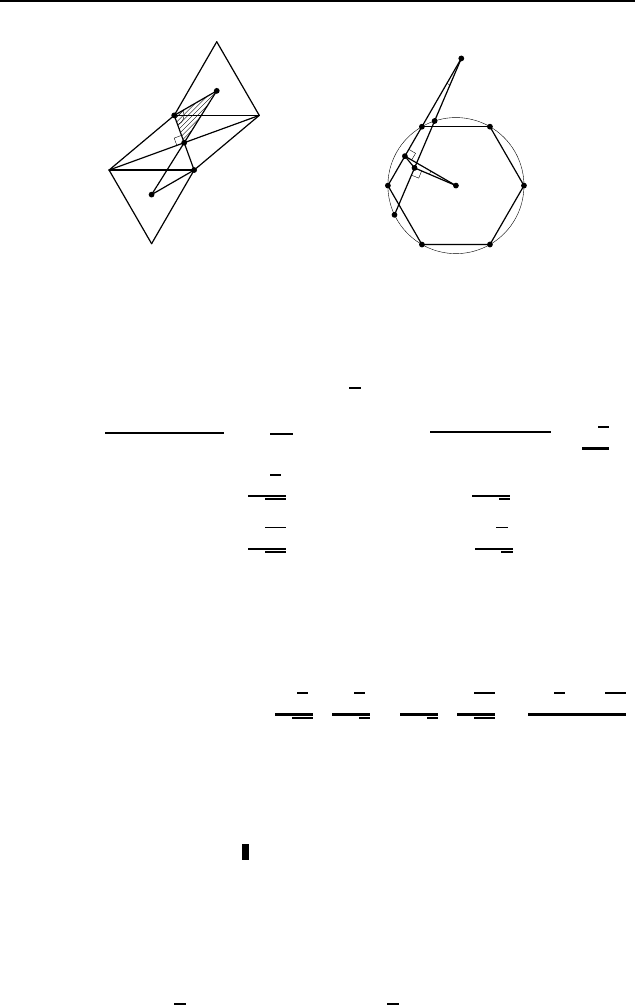
Первый спосо б .
Пусть O — центр окружности; P , Q — середины хорд N H и AF
(рис. 550). Поскольку KA ·F K = KN ·KH, то (
√
11 −1)(
√
11 +
+ 1) = 2(2 + NH). Отсюда находим, что N H = 3, KH = KN +
+ NH = 5.
§ 3.2 367
O
A
B
C
D
M
N
P
Q
Рис. 549
O
Q
P
N
A
B
C
DE
F
H
K
Рис. 550
Далее последовательно находим:
OQ =
√
3,
KO =
p
KQ
2
+ OQ
2
=
√
14, OP =
p
KO
2
− KP
2
=
√
7
2
,
sin ∠QKO =
√
3
√
14
, sin ∠P KO =
1
2
√
2
,
cos ∠QKO =
√
11
√
14
, cos ∠P KO =
√
7
2
√
2
.
Следовательно,
sin ∠HKF = sin(∠QKO − ∠P KO) =
=
√
3
√
14
·
√
7
2
√
2
−
1
2
√
2
·
√
11
√
14
=
7
√
3 −
√
77
28
.
Второй с пособ. Выразим с помощью теоремы косинусов от-
резок P Q из треугольников KP Q и OP Q и решим полученное
уравнение относительно косинуса искомого у гла.
3.100. 5 : 10 : 13.
Пусть K, L и N — точки касания
вписанной окружности со сторонами AC, BC и AB соответ-
ственно (рис. 551); F и Q — точки пересечения окружности с
медианой BM (F — между B и Q). Предположим, что точ-
ка K расположена между точками M и C. Обозначим BC = a,
BF = F Q = QM = x. Тогда BL
2
= BQ · BF = 2x
2
. По-
этому BL = x
√
2, BN = BL = x
√
2. Аналогично находим,

368 9 класс
F
A
B
C K
L
M
N
Q
Рис. 551
A
B
C
D
M
N
P
Q
Рис. 552
что KM = x
√
2, а так как CL = CK, то
MC = BC = a, AC = 2a,
AB = AN + N B = a + x
√
2 + x
√
2 = a + 2x
√
2.
Выразим медиану BM через стороны треугольника ABC
(см. задачу 3.66
0
):
4·BM
2
= 2BC
2
+2AB
2
−AC
2
, или 36x
2
= 2(a+2x
√
2)
2
+2a
2
−4a
2
.
Из этого уравнения находим, что a =
5x
√
2
4
. Тогда
BC = a = 5x
√
2
4
, AC = 2a = 5x
√
2
2
,
AB = a + 2x
√
2 = 13x
√
2
4
.
Следовательно, BC : CA : AB = 5 : 10 : 13.
3.101. 2
√
10. Пусть P и Q — проекции точки D на AB
и AC, M и N — проекции точек B и C на прямую AD (рис. 552).
Обозначим ∠BAD = , ∠CAD = , AB = a, AC = b. Тогда
cos
=
AP
AD
=
4
5
, sin
=
3
5
,
cos
=
AQ
AD
=
2
√
5
, sin =
1
√
5
,
BM = AB sin
=
3a
5
, CN = AC · sin
=
b
√
5
.
Из равенства прямоугольных треугольников CND и BMD сле-
дует, что BM = CN, т. е.
3a
5
=
b
√
5
. Отсюда находим, что b =
3a
√
5
.
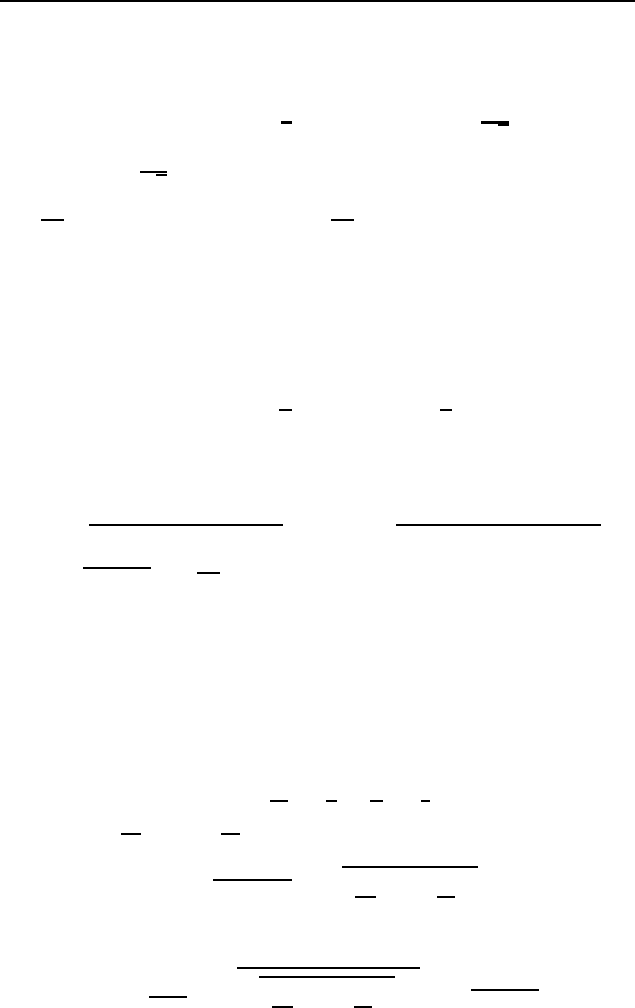
§ 3.2 369
Выразив равные отрезки BD и CD по теореме косинусов из
треугольников BAD и CAD соответственно, получим уравне-
ние:
a
2
+ 25 − 2a · 5 ·
4
5
= b
2
+ 25 − 2b · 5 ·
2
√
5
.
Заменив b на
3a
√
5
, найдем a = 5.
По теореме косинусов из треугольника BAD найдем BD =
=
√
10. Следовательно, BC = 2
√
10.
3.102. Указание. Выразите косинус угла ABC по теореме
косинусов из треугольников ABC и ABD и приравняйте полу-
ченные выражения.
3.103. Первый спосо б . Заметим, что
a
4
+ b
4
= a
4
+ 2a
2
b
2
+ b
4
− 2a
2
b
2
= (a
2
+ b
2
)
2
− 2a
2
b
2
=
= (a
2
+ b
2
−
√
2ab)(a
2
+ b
2
+
√
2ab) =
= (a
2
+ b
2
− 2ab cos 45
◦
)(a
2
+ b
2
−2ab cos 135
◦
).
Пусть
p =
p
a
2
+ b
2
−2ab cos 45
◦
, q =
p
a
2
+ b
2
− 2ab cos 135
◦
.
Тогда
4
√
a
4
+ b
4
=
√
pq.
Отсюда вытекает следующее построение. Строим треуголь-
ник со сторонами a и b и углом 45
◦
между ними. Тогда p —
третья сторона этого треугольника. Отрезок q — третья сторо-
на треугольника со сторонами a и b и углом 135
◦
между ними.
Наконец, искомый отрезок x строим как среднее геометрическое
отрезков p и q (см. задачу 2.204).
Второй способ. Пусть c — произвольный отрезок. Построим
такие отрезки m и n, что
m
a
=
a
c
и
n
b
=
b
c
(см. задачу 2.545).
Тогда m =
a
2
c
и n =
b
2
c
. Затем построим такой отрезок y, что
y =
p
m
2
+ n
2
=
r
a
2
c
2
+
b
2
c
2
,
далее — такой отрезок x, что
x =
√
y · c =
s
r
a
2
c
2
+
b
2
c
2
· c =
4
p
a
4
+ b
4
.
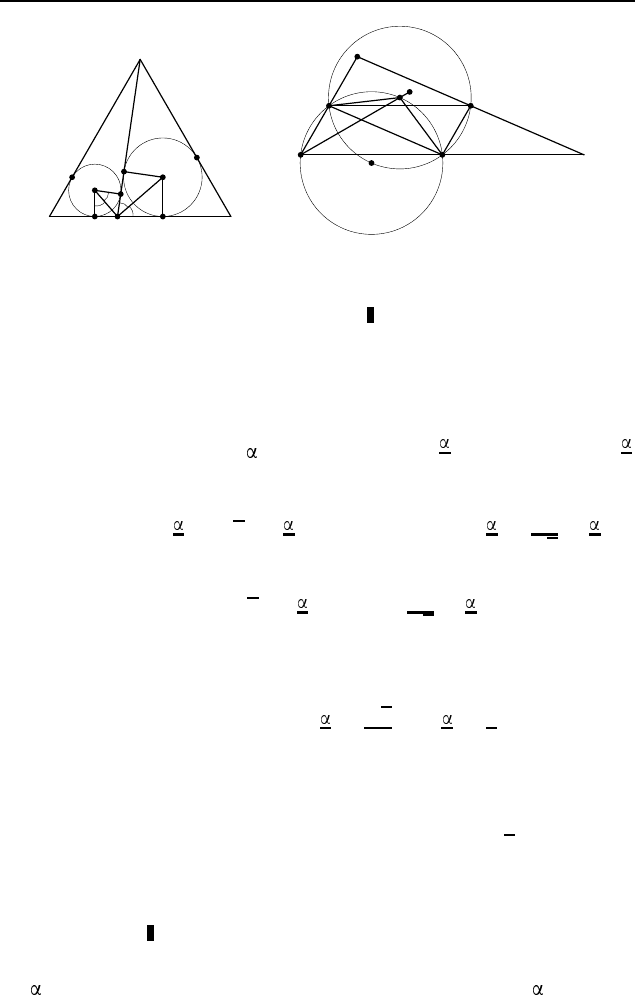
370 9 класс
B
A C
O
1
O
2
E
F
D
M
N
P
Q
Рис. 553
A
O
M
B
A
1
B
1
C
C
1
Рис. 554
3.104. AB = BC = AC = 8.
Пусть O
1
и O
2
— цен-
тры окружностей, P и Q — их точки касания со стороной AC,
E и F — с отрезком BD (рис. 553). Обозначим DP = x. То-
гда DQ = DF = DE + EF = DE + BE − BF = DE + BM −
− BN = x + 1.
Обозначим ∠BDC =
. Тогда ∠O
2
DQ =
2
, ∠O
1
DP = 90
◦
−
2
(так как ∠O
1
DO
2
= 90
◦
). Поэтому
DQ = O
2
Q ctg
2
=
√
3 ctg
2
, DP = P O
1
tg
2
=
2
√
3
tg
2
,
или
x + 1 =
√
3 ctg
2
, x =
2
√
3
tg
2
.
Перемножив эти равенства почленно, получим уравнение
x(x + 1) = 2. Отсюда находим, что x = 1 (второй корень не
подходит). Поэтому BD = 7, tg
2
=
√
3
2
, cos
2
=
1
7
.
Обозначим CQ = CN = y. По теореме косинусов из тре-
угольника BDC находим
(5 + y)
2
= 49 + (2 + y)
2
− 2 · 7 · (2 + y) ·
1
7
.
Откуда y = 3. Аналогично находим, что AP = AM = 2. Следо-
вательно, AB = BC = AC = 8.
3.105. 10.
Пусть A
1
, B
1
и C
1
— середины BC, AC и AB
соответственно, O — центр данной окружности, ∠ACB =
= (рис. 554). Поскольку ∠A
1
C
1
B
1
= ∠ACB = , то тре-
угольник A
1
B
1
C
1
равен треугольнику B
1
A
1
C. Следовательно,
