Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

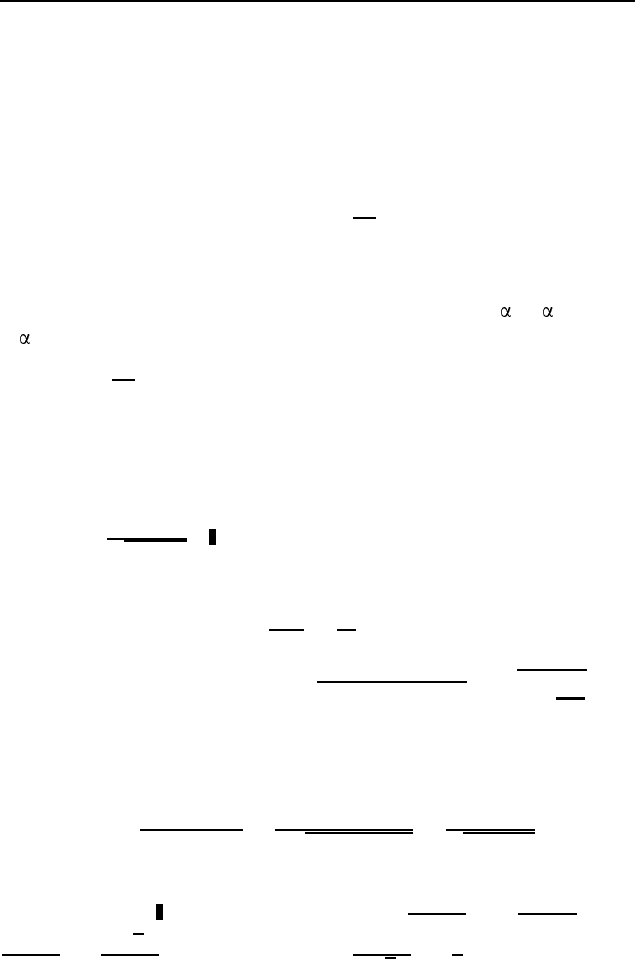
§ 3.3 371

радиусы данной окружности и окружности, описанной около

треугольника A

C, равны.

Пусть прямая OC пересекает вторую окружность в точ-

ке M. Тогда MA

= MB

(точка M лежит на биссектрисе

угла ACB) и OA

= OB

. Поэтому если точки O и M не

совпадают, то OC ⊥ A

, а так как CO — биссектриса

угла ACB, то CA

= CB

и AC = BC = 4. В этом слу-

чае AC + BC = 4 + 4 = 8 < 2

√

19 = AB, что невозможно.

Значит, предположение о том, что точки M и O не совпадают,

не верно. Таким образом, центр второй окружности лежит на

первой. Тогда ∠A

+ ∠A

= 180

◦

, т. е. 2

+ = 180

◦

= 60

◦

Обозначим AC = x. Тогда по теореме косинусов x

+ 16 −

− 4x = (2

√

19)

. Из этого уравнения находим, что x = 10.

§ 3.3

3.106. 4. Указание. Воспользуйтесь теоремой синусов.

3.107.

√

−a

. Пусть D — середина основания BC рав-

нобедренного треугольника ABC со сторонами AB = AC = b

и BC = a (рис. 555). Из прямоугольного треугольника ADB

находим, что cos ∠ABD =

. Тогда

sin ∠ABC = sin ∠ABD =

1 − cos

∠ABD =

1 −

Следовательно, если R — радиус окружности, описанной около

треугольника ABC, то

R =

2 sin ∠ABC

1 − a

/(4b

)

√

− a

3.108. 30

◦

или 150

◦

3.109. 30

◦

По теореме синусов

sin ∠A

sin ∠B

, или

sin ∠A

√

sin 45

◦

, откуда sin ∠A =

sin 45

◦

√

. Следовательно,

∠A = 30

◦

или ∠A = 150

◦

. Во втором случае ∠A + ∠B = 150

◦

+ 45

◦

, что невозможно.

372 9 класс

B C

Рис. 555

Рис. 556

B C

Рис. 557

3.110.

√

6+3

√

Пусть CD — биссектриса прямоуголь-

ного треугольника ABC (рис. 556), проведенная из вершины C

прямого угла, ∠A = 30

◦

, CD = a. Из треугольника CBD

по теореме синусов находим, что

sin ∠BCD

sin ∠B

, откуда

BD =

CD sin ∠BCD

sin ∠B

a sin 45

◦

sin 60

◦

√

Аналогично из треугольника CAD находим, что AD = a

√

Следовательно,

AB = BD + AD =

√

+ a

√

2 =

√

6 + 3

√

3.111.

Пусть — угол, противолежащий стороне, рав-

ной 15. Тогда по теореме косинусов

cos

169 + 196 − 225

2 · 13 · 14

Следовательно, если R — радиус окружности, описанной около

данного треугольника, то

R =

2 sin

1 −





2 ·

3.112.

Пусть F — проекция конца C меньше-

го основания BC равнобокой трапеции ABCD на большее ос-

нование AD (рис. 557). Тогда отрезок AF равен средней ли-

нии трапеции (см. задачу 2.118

), а так как в прямоугольном

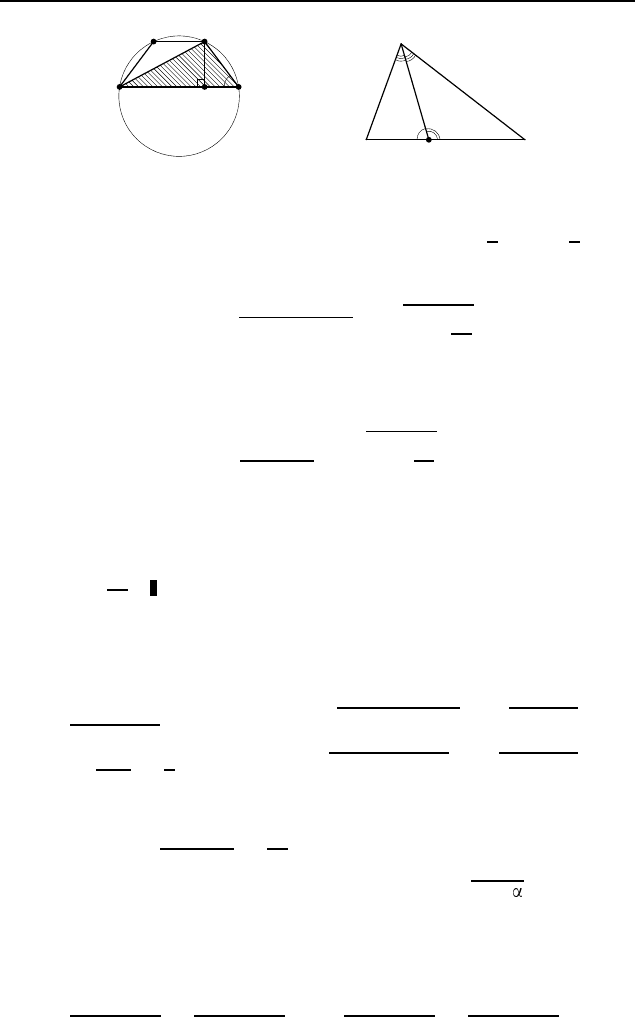
§ 3.3 373

B C

Рис. 558

B CD

Рис. 559

треугольнике CF D угол D равен 30

◦

, то CF =

CD =

a. Из

прямоугольного треугольника ACF находим, что

AC =

+ CF

Если R — радиус окружности, описанной около треугольни-

ка ACD, то

R =

2 sin ∠D

Осталось заметить, что окружность, описанная около треуголь-

ника ACD, совпадает с окружностью, описанной около трапе-

ции ABCD.

3.113.

Из конца C меньшего основания BC трапе-

ции ABCD опустим перпендикуляр CK на большее основа-

ние AD (рис. 558). Тогда CK = 8. Если AD = 21, BC = 9,

то

KD =

AD − BC

= 6, CD =

+ DK

+ 6

= 10,

sin ∠D =

, AC =

+ CK

+ 8

= 17.

Если R — радиус окружности, описанной около трапеции

ABCD, то R =

2 sin ∠D

3.114. Указание. Примените формулу R =

2 sin

3.115. Пусть AD — биссектриса треугольника ABC

(рис. 559). Применяя теорему синусов к треугольникам ABD

и ACD, получим равенства

sin ∠BAD

sin ∠ADB

sin ∠CAD

sin ∠ADC

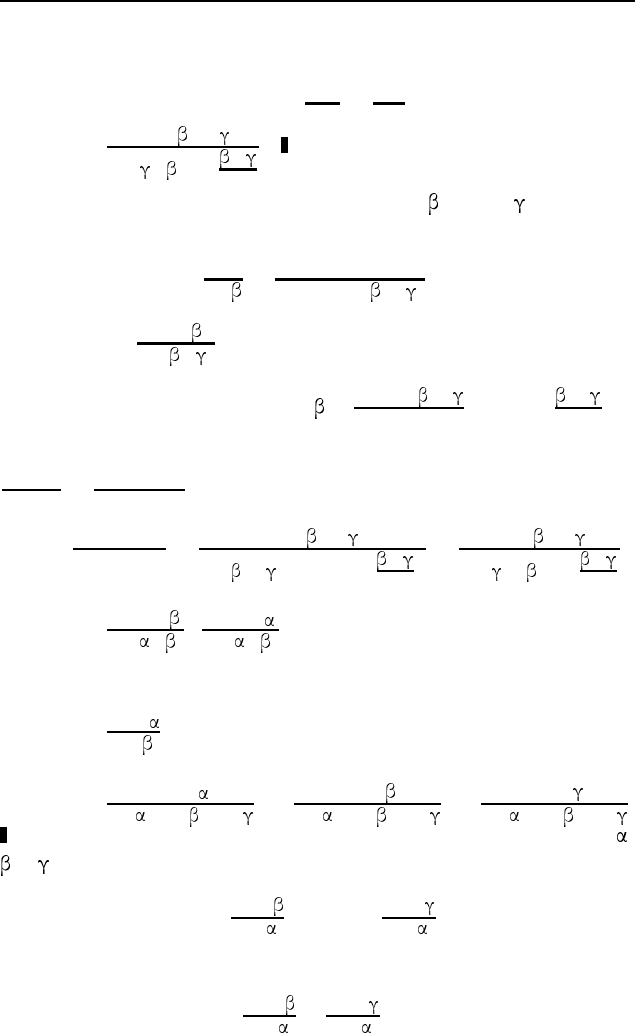
374 9 класс

Поскольку ∠BAD = ∠CAD и sin ∠ADC = sin(180

◦

−∠ADB) =

= sin ∠ADB, то, разделив почленно первое равенство на второе,

получим требуемое равенство

3.116.

a sin

sin

sin( + ) cos

−

Пусть AD — биссектриса тре-

угольника ABC, в котором BC = a, ∠B =

, ∠C = (рис. 560).

По теореме синусов

sin

sin(180

◦

− − )

откуда AC =

a sin

sin( + )

. По теореме о внешнем угле треугольника

∠ADC = ∠ABD + ∠BAD =

180

◦

−

= 90

◦

−

По теореме синусов из треугольника ADC находим, что

sin ∠C

sin ∠ADC

, откуда

AD =

AC sin ∠C

sin ∠ADC

a sin

sin

sin( + ) sin



◦

−



a sin

sin

sin( + ) cos

−

3.117.

2m sin

sin( + )

2m sin

sin( + )

. Указание. На продолжении меди-

аны AM за точку M отложите отрезок MK, равный AM , и

примените теорему синусов к треугольнику ACK.

3.118.

a sin

sin

. Указание. Докажите, что CM = DM, а DM

найдите из треугольника ADM по теореме синусов.

3.119.

P sin

sin +sin +sin

P sin

sin +sin +sin

P sin

sin +sin +sin

Обозначим стороны треугольника, противолежащие углам ,

и , через a, b и c соответственно. По теореме синусов

b =

a sin

sin

и c =

a sin

sin

Поскольку a + b + c = P , имеем уравнение

a +

a sin

sin

a sin

sin

= P,

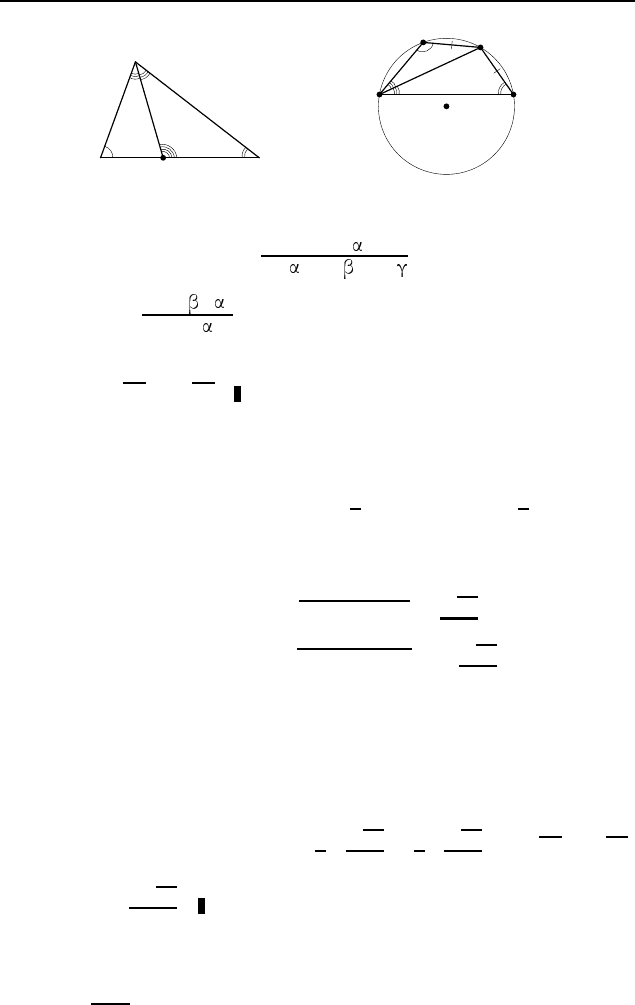
§ 3.3 375

B CD

Рис. 560

Рис. 561

откуда находим, что a =

P sin

sin +sin +sin

. Аналогично находим

b и c.

3.120. b +

a sin( − )

2 sin

. Указание. Через конец меньшего осно-

вания трапеции проведите прямую, параллельную противопо-

ложной боковой стороне.

3.121.

√

35 ±

√

15. Пусть R = 12 — радиус окружности

(рис. 561). Тогда

AB = 2R sin ∠ACB, BC = 2R sin ∠BAC.

Отсюда находим, что sin ∠ACB =

и sin ∠BAC =

. Посколь-

ку сторона BC треугольника ABC не наибольшая, то угол A

острый и его косинус положительный. Следовательно,

cos ∠BAC =

1 − sin

∠A =

√

cos ∠ACB = ±

1 − cos

∠B = ±

√

Тогда

AC = 2R sin ∠ABC = 2R sin(∠BAC + ∠ACB) =

= 2R(sin ∠A cos ∠C + cos ∠A sin ∠C) =

= 2 · 12(±

√

) =

√

35 ±

√

15.

3.122. 4,

√

Поскольку около трапеции можно описать

окружность, то трапеция равнобокая. Пусть r и R — радиусы

вписанной и описанной окружностей. Точка касания вписанной

окружности делит боковую сторону на отрезки 2 и 8. Поэто-

му r =

√

2 · 8 = 4.

376 9 класс

Диагональ трапеции — гипотенуза прямоугольного тре-

угольника с катетами 8 (высота трапеции, опущенная из конца

меньшего основания на большее) и 10 (проекция диагонали на

большее основание, равная длине средней линии). Эта диаго-

наль видна из конца большего основания трапеции под углом

синус которого равен 4/5 (угол боковой стороны с основанием).

Следовательно,

R =

√

+ 10

2 sin

√

8/5

√

3.123.

√

. Точка C лежит на окружности, описанной

около построенного равностороннего треугольника (60

◦

+120

◦

= 180

◦

). Поэтому искомое расстоя ние равно радиусу этой

окружности, т. е.

R =

2 sin 60

◦

√

3.124. 1.

Пусть O — центр вписанной окружности тре-

угольника ABC со сторонами AC = 1, AB = 2 и углом CAB,

равным 60

◦

(рис. 562). По теореме косинусов находим, что BC =

√

3. Поскольку O — точка пересечения биссектрис треуголь-

ника ABC,

∠BOC = 90

◦

∠CAB = 90

◦

+ 30

◦

= 120

◦

(см. задачу 1.116

). Если R — искомый радиус, то

R =

2 sin ∠BOC

√

2 sin 120

◦

= 1.

3.125. Разделим почленно данное равенство на равенство

sin

. Получим равенство tg = tg . Поскольку каждый

из углов

и меньше 180

◦

, то = . Следовательно, данный

треугольник равнобедренный.

3.126.

b(a + b). Обозначим через угол, лежащий про-

тив стороны, равной b. По теореме синусов

sin 3

sin

. По-

скольку

sin 3

= sin (2 cos 2 + 1),

§ 3.3 377

Рис. 562

Рис. 563

Рис. 564

то 2b cos 2

= a − b. Тогда по теореме косинусов

= a

+ b

−2ab cos 2 = a

+ b

−a(a −b) = b

+ ab = b(a + b).

3.127. Пусть точка C лежит на окружности радиуса r, а

точка D — на окружности радиуса R (рис. 563). Тогда

BC = 2r sin ∠BAC,

BD = 2R sin ∠BAD = 2R sin(180

◦

− ∠BAC) = 2R sin ∠BAC.

Поэтому

. Значит, BA — биссектриса треуголь-

ника BCD (см. задачу 2.575

), а так как биссектрисы треуголь-

ника пересекаются в одной точке, то биссектрисы углов C и D

пересекаются на отрезке AB.

3.128. Пусть боковая сторона трапеции образует с меньшим

основанием угол, равный

. Для обеих трапеций этот угол один

и тот же, а диагональ равна произведению диаметра окружно-

сти на синус этого угла.

3.129. Пусть DE — диаметр описанной окружности, пер-

пендикулярный стороне AC треугольника ABC (рис. 564), R —

радиус этой окружности, LK — проекция диаметра DE на пря-

мую BC. Тогда

LK = DE sin ∠DEK = 2R sin ∠DEK = 2R sin ∠BCA = AB.

3.130. Пусть h

и h

— высоты треугольника ABC, прове-

денные из вершин A и C соответственно, a и c — длины от-

резков, соединяющих проекции оснований этих высот на сторо-

ны треугольника. Поскольку вершина треугольника, основание

378 9 класс

Рис. 565

Рис. 566

соответствующей высоты и проекции основания этой высоты на

стороны треугольника лежат на одной окружности, то

a = h

sin ∠A, c = h

sin ∠C,

а так как

sin ∠C

sin ∠A

= AC, то a = c.

3.131. Пусть P и Q — проекции точки M на прямые AC

и BC (рис. 565). Тогда точки M, P , Q и C лежат на окружности

с диаметром M C. Следовательно, P Q = MC sin ∠ACB. Поэто-

му P Q максимально, если M C максимально, т. е. когда MC —

диаметр описанной окружности треугольника ABC.

3.132. Первый способ. Пусть H

— точка, симметричная

точке H относительно прямой BC (рис. 566). Тогда ∠BH

C =

= ∠BHC = 180

◦

− ∠A, поэтому точка H

лежит на описан-

ной окружности треугольника ABC. Следовательно, описан-

ная окружность треугольника BHC симметрична описанной

окружности треугольника ABC относительно прямой BC.

Остальное аналогично.

Второй способ. Пусть R и R

— радиусы описанных окруж-

ностей треугольников ABC и BHC соответственно. Тогда

R =

2 sin ∠A

2 sin ∠BHC

= R

Остальное аналогично.

3.133.

√

−b

. Пусть ∠ACB = . Тогда ∠ABC = 2 . По

теореме синусов имеем:

sin

sin 2

, где 0

◦

< < 90

◦

Поэтому cos

. Тогда sin

√

−b

. Если R — радиус

§ 3.3 379

Рис. 567

Рис. 568

окружности, то

R =

2 sin

√

− b

3.134. 2

Обозначим ∠NMP = ∠P MQ = (рис. 567).

Выразим равные отрезки N P и P Q по теореме косинусов из

треугольников N MP и P MQ соответственно:

= M N

+ MP

− 2NM · MP cos

P Q

= M P

+ MQ

−2MP · MQ cos

Приравняв правые части полученных равенств, получим урав-

нение, из которого найдем, что cos = 1/4. Тогда sin =

√

15/4.

Если R — искомый радиус, то

R =

2 sin

√

15/2

= 2

3.135.

√

. Первый способ. Обозначим ∠A = , ∠B = ,

∠C =

(рис. 568). По теореме косинусов найдем косинусы этих

углов:

cos = −

, cos

Поскольку cos

< 0, то треугольник ABC тупоугольный. По-

этому точка H пересечения прямых, содержащих высоты AA

и CC

, лежит вне треугольника ABC.

Из прямоугольных треугольников CB

B и BC

H находим:

= BC cos

= 6 ·

BH =

cos ∠HBB

cos ∠ACB

cos(∠BCB

− )

cos(90

◦

− − )

sin( + )

sin cos + cos sin

√

380 9 класс

Рис. 569

Рис. 570

Второй способ. Расстояние BH от вершины B до точки H

пересечения прямых, содержащих высоты треугольника ABC,

равно удвоенному расстоянию от центра O описанной окружно-

сти до стороны AC.

Если R — радиус этой окружности, то

AO = R =

2 sin

√

Следовательно,

BH = 2

−

= 2

400

−

√

3.136.

Треугольники BP Q и BAC (рис. 569) подоб-

ны (по двум углам). Поскольку отношение их площадей рав-

но

, то коэффициент подобия равен

. Значит, AC =

= 3P Q = 6

√

2. С другой стороны, коэффициент подобия ра-

вен

= cos ∠B. Поэтому cos ∠B =

. Тогда sin ∠B =

√

Если R — радиус описанной окружности треугольника ABC,

то R =

2 sin ∠B

3.137. Если O — центр данной окружности, а R — ее радиус,

то точки P , M, Q, O лежат на окружности с диаметром MO = R

(рис. 570). Поэтому

P Q = MO sin ∠AOD = R sin ∠AOD.

3.138. По данному углу

при вершине A искомого треуголь-

ника ABC и данному радиусу R описанной окружности постро-

им противоположную сторону BC искомого треугольника.