Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

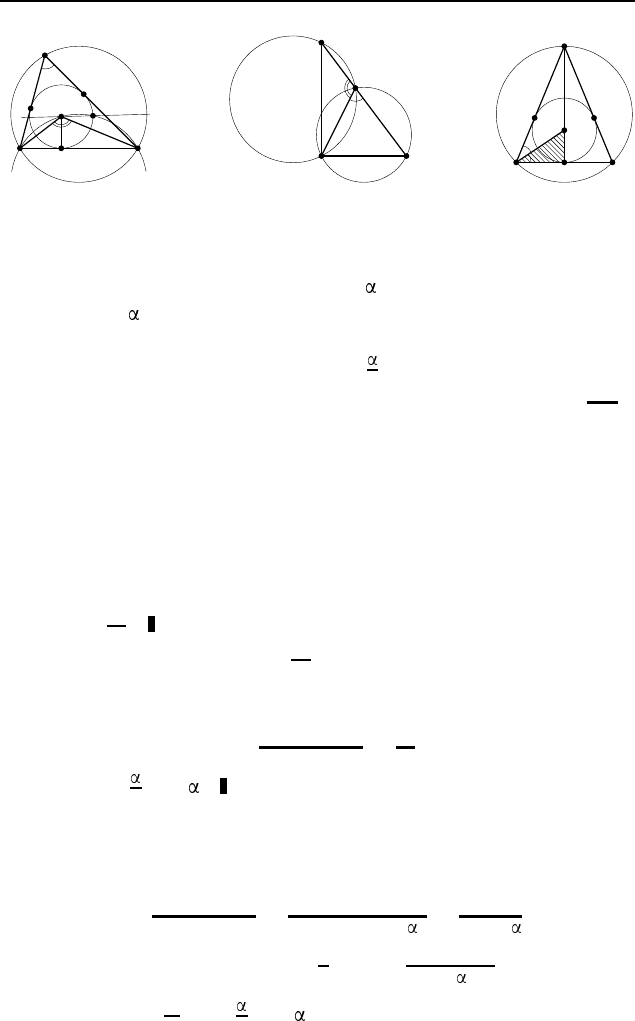
§ 3.3 381

B C

Рис. 571

Рис. 572

B C

Рис. 573

Для этого построим прямоугольный треугольник по гипо-

тенузе, равной 2R, и острому углу . Тогда катет, противоле-

жащий углу

, равен стороне BC искомого треугольника ABC.

Затем построим на найденной стороне BC (рис. 571) как на

хорде дугу, вмещающую угол 90

◦

(если O — точка пересе-

чения биссектрис треугольника ABC, то ∠BOC = 90

◦

∠A

Каждая точка пересечения этой дуги с прямой, параллельной

прямой BC и отстоящей от нее на расстояние, равное данному

радиусу вписанной окружности, есть центр вписанной окруж-

ности искомого треугольника.

Проведем эту окружность и построим к ней касательные из

точек B и C. Пересечение этих касательных есть вершина A

искомого треугольника ABC.

3.139.

Поскольку ∠ADC + ∠ADB = 180

◦

(рис. 572),

то sin ∠ADC = sin ∠ADB =

. Если R — радиус окружности,

проходящей через точки A, C и D, то b = 2R sin ∠ADC. Отсюда

находим, что

R =

2 sin ∠ADC

3.140. tg

sin 2

. Обозначим основание BC равнобедрен-

ного треугольника ABC (рис. 573) через a, радиусы вписанной

и описанной окружностей — r и R, центр вписанной окружно-

сти — O, середину BC — M. Тогда

R =

2 sin ∠BAC

2 sin(180

◦

− 2 )

2 sin 2

r = OM = BM tg



∠B



2 · tg( /2)

Следовательно,

= tg

sin 2

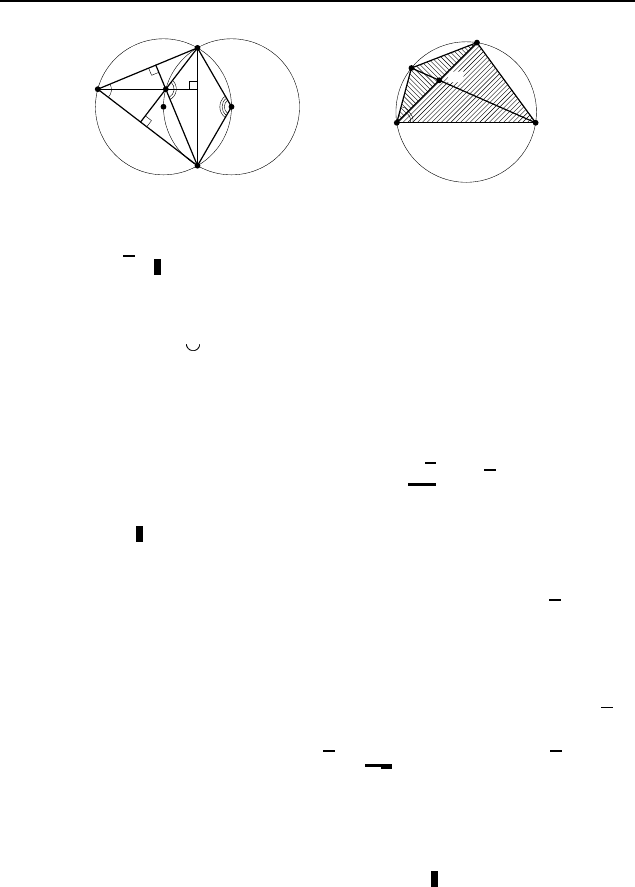
382 9 класс

Рис. 574

Рис. 575

3.141.

√

3. Если H — точка пересечения высот треуголь-

ника ABC (рис. 574), то ∠AHC = 180

◦

− ∠ABC. Тогда

∠AOC =

AHC = 360

◦

− 2∠AHC = 2∠ABC,

где O — центр второй окружности. Поскольку ∠AOC+∠ABC =

= 180

◦

, то 3∠ABC = 180

◦

. Следовательно, ∠ABC = 60

◦

. Тогда

AC = 2R sin ∠ABC = 2 · 1 ·

√

3.142. 2. Пусть AN = x, R — радиус описанной окруж-

ности (рис. 575). Тогда

BN = 2R sin 30

◦

= R, CN = 2R sin 45

◦

= R

√

По теореме косинусов для треугольников ABN и ACN:

= R

= AB

+ AN

− 2AB · AN cos 30

◦

= 1 + x

− x

√

= 2R

= 6 + x

− 2

√

6x ·

√

= 6 + x

− 2x

√

Из полученной системы уравнений находим, что x

= 4. Следо-

вательно, x = 2.

3.143. Прямая без точки и точка C.

Если BC > AC,

то построим произвольную окружность, проходящую через точ-

ки B и C. Тогда су ществует окружность того же радиуса, про-

ходящая через точки A и C. Аналогично для случая BC 6 AC.

Поэтому точка C принадлежит искомому геометрическому ме-

сту точек.

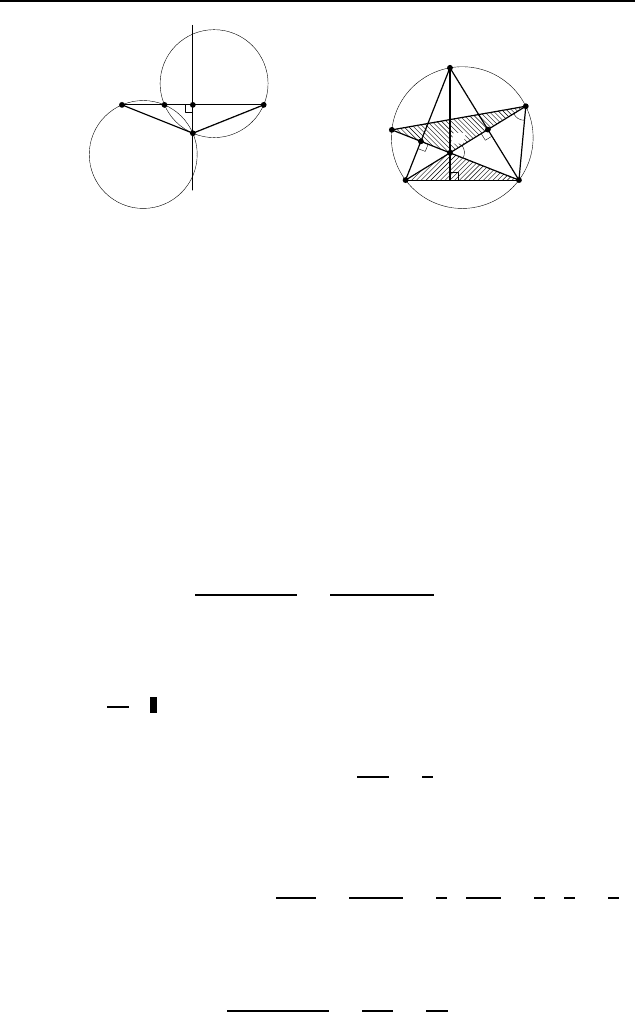
§ 3.3 383

C D

Рис. 576

Рис. 577

Пусть M — произвольная точка искомого геометрическо-

го места точек, отличная от C и от середины D отрезка AB

(рис. 576). Тогда ∠M AB = ∠M BA (как углы, вписанные в

равные окружности и опирающиеся на равные дуги). Следова-

тельно, треугольник AMB равнобедренный и точка M лежит

на серединном перпендикуляре к отрезку AB.

Пусть теперь P — произвольная точка серединного перпен-

дикуляра к отрезку AB, отличная от его середины D. Тогда

радиусы окружностей, описанных около треугольников ACP

и BCP , равны, так как

P C

2 sin ∠P AC

P C

2 sin ∠P BC

Следовательно, точка P принадлежит рассматриваемому гео-

метрическому месту точек.

3.144.

Пусть H — точка пересечения высот треуголь-

ника ABC (рис. 577). Тогда треугольник QHP подобен тре-

угольнику AHC с коэффициентом

Поскольку ∠P CB = ∠P AB = ∠QCB, то CM — биссектриса

и высота треугольника HCP . Поэтому HM = MP . Тогда

cos ∠AP C = cos ∠MHC =

HP/2

а sin ∠AP C = 4/5. Если R — искомый радиус, то

R =

2 sin ∠AP C

8/5

384 9 класс

3.145. 17. Первый способ. Пусть AD, BE и CF — вы-

соты остроугольного треугольника ABC (рис. 578); DF = 8,

EF = 15, DE = 17. Поскольку 8

+ 15

= 17

, то треуголь-

ник DEF прямоугольный, ∠DF E = 90

◦

. Обозначим через

угол C треугольника ABC. Тогда треугольник CDE подо-

бен треугольнику CAB (по двум углам) с коэффициентом

k =

= cos ∠BCE = cos

Поскольку

◦

= ∠DF E = 180

◦

− ∠AF E − ∠BF D = 180

◦

− 2

(см. задачу 2.613

), то = 45

◦

Пусть R

и R — радиусы окружностей, описанных около тре-

угольников CDE и CAB. Тогда

2 sin ∠DCE

2 sin 45

◦

√

Следовательно, R =

√



cos 45

◦

= 17.

Второй способ. Образы H

, H

и H

точки H пересечения

высот треугольника ABC (см рис. 578) при симметрии отно-

сительно прямых BC, AC и AB расположены на окружности,

описанной около треугольника ABC (см. задачу 2.644

), поэто-

му искомый радиус равен радиусу окружности, описанной около

треугольника H

. Этот треугольник подобен прямоуголь-

ному треугольнику F DE с коэффициентом 2. Значит, треуголь-

ник H

прямоугольный, его гипотенуза H

равна 34, а

радиус описанной окружности равен 17.

3.146.

√

rR,

Обозначим ∠ACN = , ∠ADN =

(рис. 579). Тогда

AC = 2R sin

, AD = 2r sin ,

sin

или

2R sin

sin

2r sin

sin

Отсюда находим, что

sin

. Если R

— радиус

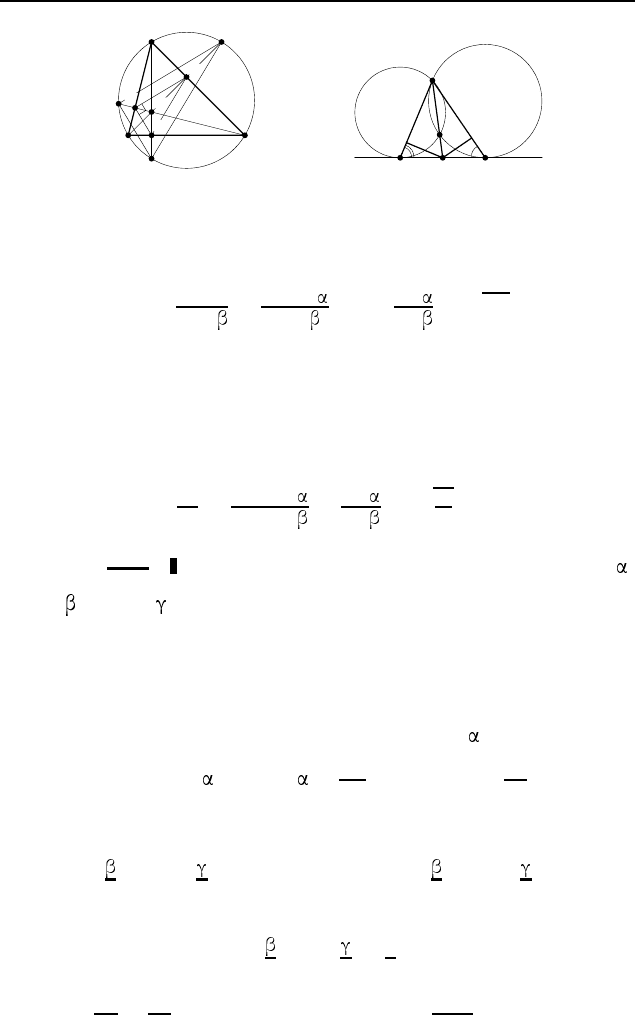
§ 3.3 385

Рис. 578

CD N

Рис. 579

окружности, описанной около треугольника ACD, то

2 sin

2R sin

2 sin

= R ·

sin

√

rR.

По теореме о касательной и секущей

= N A · NB и DN

= N A · NB.

Поэтому CN = DN . Если h

и h

— указанные высоты, то

CN sin

DN sin

sin

3.147.

r+R

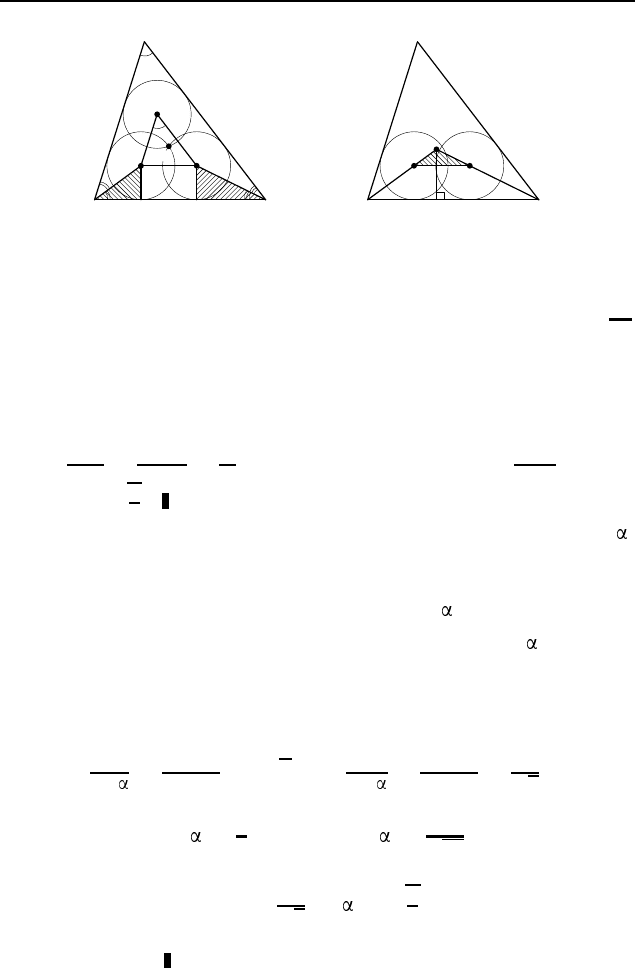
Первый способ. Обозначим BC = a, ∠A = ,

∠B =

, ∠C = (рис. 580, а), O

, O

— центры указанных

равных окружностей, вписанных в углы A, B и C соответствен-

но, M — их общая точка, x — искомый радиус. Поскольку x —

радиус окружности, описанной около треугольника O

, то

= 2x sin ∠O

= 2x sin

a = 2R sin

, sin =

, O

С другой стороны,

x ctg

+ x ctg

+ O

= a, r ctg

+ r ctg

= a,

или

ctg

+ ctg

Поэтому

= a. Следовательно, x =

r+R

386 9 класс

B C

а)

B C

б )

Рис. 580

Второй способ . Будем считать известным, что O

(см. первый способ). Лучи BO

и CO

пересекаются в центре O

вписанной окружности треугольника ABC (рис. 580, б ). Высоты

подобных треугольников OO

и OBC, проведенные из общей

вершины O, относятся как основания этих треугольников. По-

этому

r−x

. Отсюда находим, что x =

R+r

3.148.

Пусть M — точка пересечения диагоналей

четырехугольника ABKC (рис. 581). Обозначим ∠BAK =

Тогда

∠KM C = ∠AMB = 60

◦

−

∠BCK = 180

◦

− ∠KMC − ∠MKC = 90

◦

Применяя теорему синусов к треугольникам ABK и BCK, по-

лучим

sin

sin 30

◦

= 2

√

cos

sin 60

◦

√

откуда находим tg

. Значит, cos

√

. Следовательно,

BK =

√

cos

3.149. 12,5.

Пусть O — центр окружности, вписанной в

треугольник ABC (рис. 582), Q — центр окружности, проходя-

щей через точки C, O и M (пересечение биссектрисы угла A

§ 3.3 387

Рис. 581

Рис. 582

со стороной BC), CP — диаметр этой окружности. Обозначим

∠OCA = ∠OCB =

. Тогда

∠OMP = ∠OCP =

, ∠AMC = ∠AMP + ∠P MC = + 90

◦

∠MAC = 180

◦

− ∠AMC − ∠MCA =

= 180

◦

− (

+ 90

◦

) − 2 = 90

◦

− 3 ,

∠BAC = 2∠MAC = 180

◦

−6

∠ABC = 180

◦

− ∠ACB − ∠BAC =

= 180

◦

− 2 − (180

◦

− 6 ) = 4 .

По теореме синусов в треугольнике ABC имеем:

sin 2

sin 4

, или

sin 2

2 sin 2 cos 2

Отсюда находим, что

cos 2 =

, sin 2

Если R — радиус окружности, описанной около треугольни-

ка ABC, то R =

2 sin 2

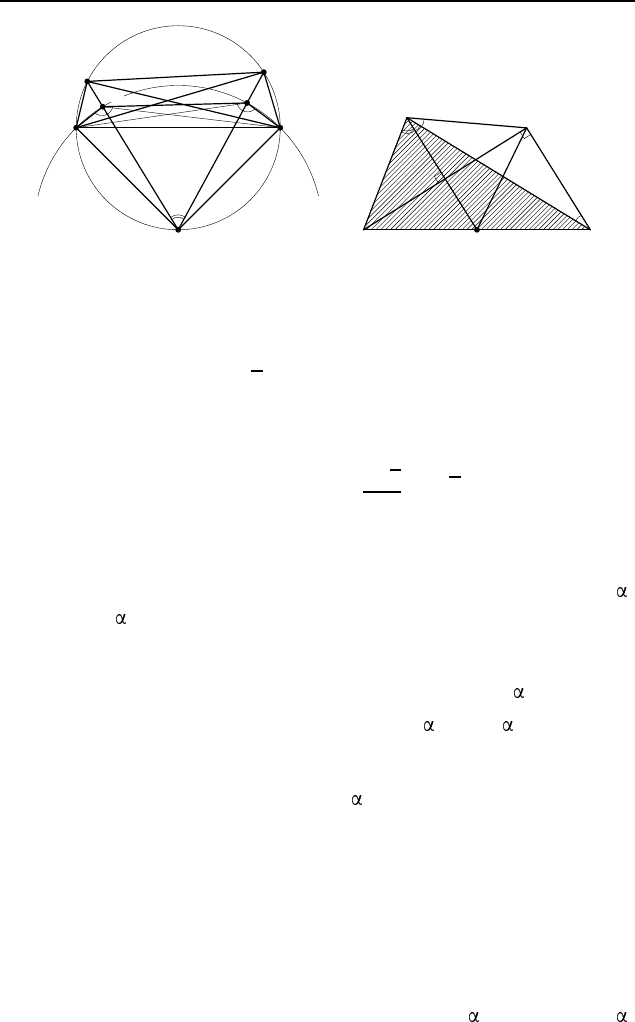
3.150.

√

3. Пусть O

и O

— центры окружностей

(рис. 583), вписанных в треугольники ABD и ACD. Поскольку

∠AO

D = ∠AO

D = 135

◦

(см. задачу 1.116

), то точки A, O

и D лежат на одной окружности. Пусть O — центр этой

окружности, R — ее радиус. Тогда

AD = 2R sin ∠AO

D, или 2 = 2R sin 135

◦

Откуда находим, что R =

√

388 9 класс

Рис. 583

Рис. 584

Поскольку ∠AOD = 90

◦

, то точка O лежит на окружности,

описанной около данного четырехугольника ABCD; ∠O

= 60

◦

= R =

√

2) и AO = OD. Тогда CO и BO —

биссектрисы углов ACD и ABD. Поэтому BO

O — одна прямая

и CO

O — одна прямая. Поскольку ∠BOC = 60

◦

, то

BC = AD sin 60

◦

√

3.151. Первый способ. Предположим, что нужный треуголь-

ник ABC построен (рис. 584). Пусть BC = a и AC = b —

его данные стороны, CM — медиана. Обозначим ∠ACM =

∠BCM = 2

. Если E — точка, симметричная вершине B отно-

сительно прямой CM, то

CE = CB = a, ∠ECM = ∠BCM = 2

∠ECA = ∠ECM − ∠ACM = 2

−a = .

Поскольку ME = M B = MA, то ∠AEB = 90

◦

. Поэто-

му AE k MC, ∠EAC = ∠MCA =

. Следовательно, треуголь-

ник AEC — равнобедренный, т. е. AE = EC = a.

Отсюда вытекает следующее построение. Строим равнобед-

ренный треугольник ACE по трем сторонам. Через вершину C

проводим прямую, параллельную AE. Образ точки E при сим-

метрии относительно этой прямой есть искомая вершина B.

Второй способ. Предположим, что ну жный треугольник

ABC построен. Пусть BC = a и AC = b — его данные сто-

роны, CM — медиана. Обозначим ∠ACM =

, ∠BCM = 2 .

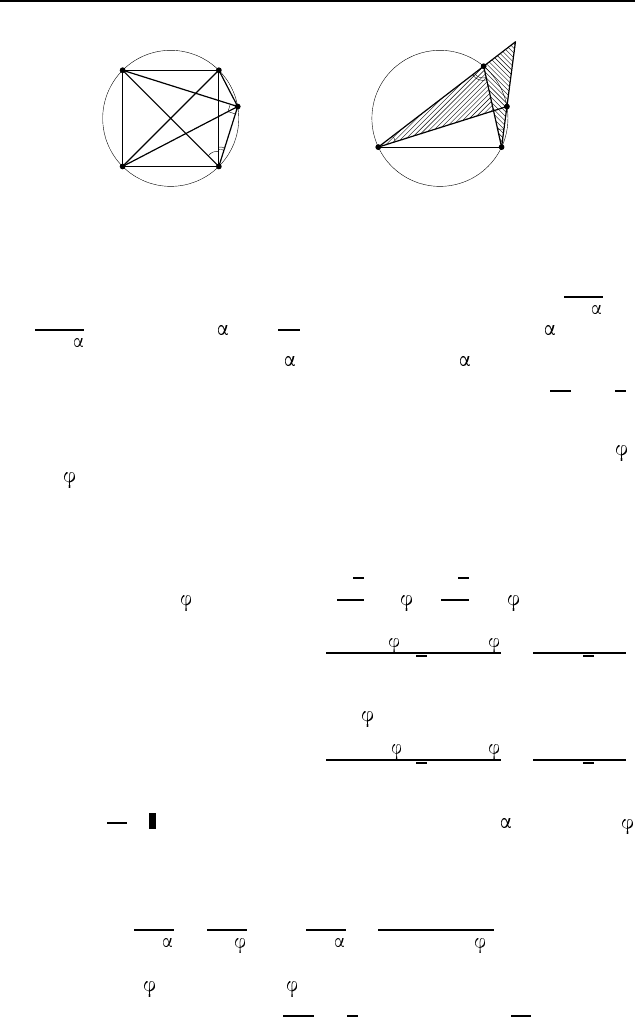
§ 3.3 389

A B

Рис. 585

Рис. 586

Достроим треугольник ABC до параллелограмма BCAD. По

теореме синусов из треугольника BCD находим, что

sin

sin 2

, откуда cos =

. Следовательно, угол

можно

построить. Поскольку 0 < 3

< 180

◦

, то 0 < < 60

◦

. Поэтому

задача имеет решение (и притом единственное) при

или b > a.

3.152. Пусть CK < AK (рис. 585). Обозначим ∠ACK =

Тогда

> 45

◦

. Точка K лежит на окружности, описанной около

данного квадрата. Если R — радиус этой окружности, то

BK = 2R sin ∠BCK =

= AC sin(

− 45

◦

) = AC



√

sin

−

√

cos



AC sin

− AC cos

√

AK − CK

√

DK = 2R sin ∠KCD = AC sin(45

◦

) =

AC cos

+ AC sin

√

CK + AK

√

3.153.

Обозначим ∠BAM = ∠BCM = , ∠ABL =

(рис. 586). По теореме синусов из треугольников ABL и BCK

находим, что

sin

sin(180

◦

− )

Поскольку sin

= sin(180

◦

− ), то, разделив почленно получен-

ные равенства, найдем, что

, откуда BL =

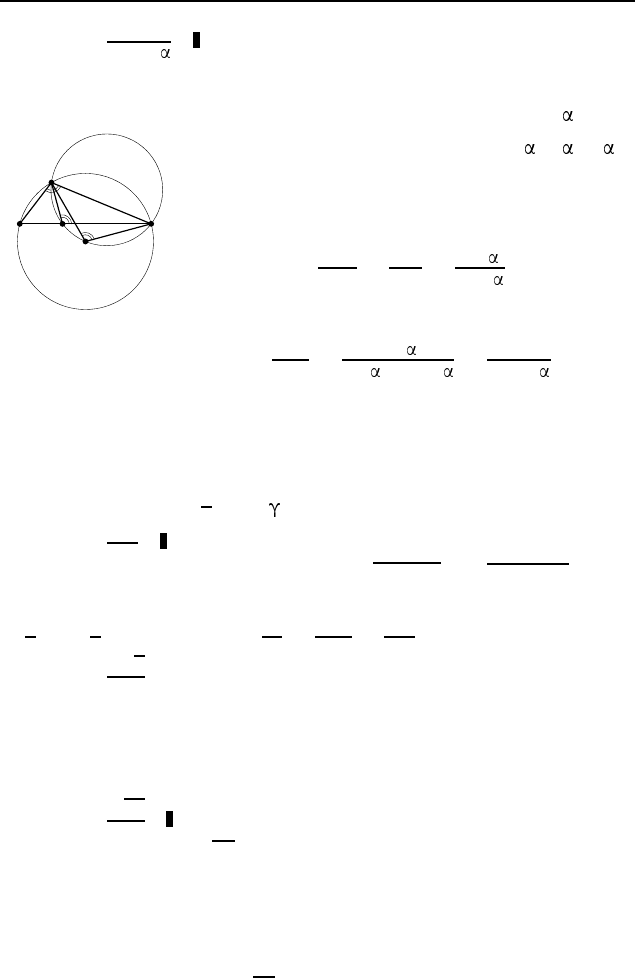
390 9 класс

3.154.

4 cos

. Пусть O — центр окружности, описанной

Рис. 587

около треугольника ABC (рис. 587). Тогда

∠AMC = ∠AOC = 2∠ABC = 2

∠BMC = ∠AMC − ∠MBC = 2

− = .

Значит, CM — биссектриса треугольни-

ка ACB. Следовательно,

sin

sin 3

Поэтому

sin

sin + sin 3

4 cos

§ 3.4

3.155. Прямоугольный треугольник. Указание. Воспользуй-

тесь формулой S =

ab sin

3.156.

120

Пусть a и b — катеты данного треугольника

(a = 15, b = 8), c — гипотенуза (c =

√

+ b

√

225 + 64 = 17),

h — искомая высота, S — площадь треугольника. Тогда S =

ab =

ch. Откуда h =

15·8

120

3.157.

√

. Указание. Докажите, что треугольник ABE

равнобедренный.

3.158. Указание. Площадь четырехугольника с вершинами

в серединах данного выпуклого четырехугольника в два раза

меньше площади данного четырехугольника (см. задачу 2.478).

3.159.

√

Пусть в треугольнике ABC известны сторо-

ны AB = 1, AC =

√

15 и медиана AM = 2 (рис. 588). На про-

должении медианы AM за точку M отложим отрезок MK, рав-

ный AM. Тогда четырехугольник ABKC — параллелограмм,

поэтому CK = AB = 1. Площадь треугольника ABC равна

площади треугольника ACK, все стороны которого известны:

AK = 2AM = 4, AC =

√

15, CK = 1. Поскольку AK

= AC

+ CK

(16 = 15 + 1), то треугольник ACK прямоугольный