Graef M. Introduction to conventional transmission electron microscopy

Подождите немного. Документ загружается.

118 Basic quantum mechanics

The probability P is given by the bra-ket:

P =

2πik



·r

V (r)

2πik·r



2πik



·r

2πig·r

2πik·r



...

2πi(k+g−k



)·r

dr,



δ(k + g − k



This expression is only different from zero whenever k + g = k



, which is the Bragg

equation in reciprocal space. In such a situation, the probability amplitude P is

equal to the Fourier coefﬁcient V

Example 2.4 Determine for which reciprocal lattice vectors g the Fourier coefﬁ-

cient V

(equation 2.83) vanishes in a structure with a face-centered cubic lattice.

Answer: The summation over all the atoms in the unit cell can be written as a sum-

mation over one-quarter of the atoms and a summation over all atoms equivalent

to each other by the Bravais lattice N

centering vectors R





j=1

−2πig·r

;



N/4



j=1

−2πig·r



k=1

−2πig·R

;



N/4



j=1

−2πig·r

1 + e

−πig·(a+b)

+ e

−πig·(a+c)

+ e

−πig·(b+c)

;

1 + (−1)

h+k

+ (−1)

h+l

+ (−1)

k+l



N/4



j=1

−2πig·r

We have used the fact that g · (a + b) = h + k, and also e

−πin

= (−1)

−n

= (−1)

All reciprocal lattice points for which the Miller indices have mixed parity have

a vanishing Fourier coefﬁcient V

, and will not give rise to a diffracted beam.

Reﬂections which are absent because of the Bravais lattice centering symmetry are

known as systematic absences or systematic extinctions.

2.6 The electrostatic lattice potential 119

2.6.3 Finite crystal size effects

We deﬁne the shape function D(r) of a crystal as a function which equals 1 inside

the crystal and 0 outside:

D(r) =

1 inside;

0 outside.

(2.85)

The ﬁnite crystal potential V

(r) then becomes the product of the potential for the

inﬁnite crystal and the shape function:

(r) = V (r)D(r). (2.86)

We can now apply the multiplication theorem to determine how the ﬁnite character

of the crystal affects the Fourier transform of the lattice potential:

(q) = F[V (r)] ⊗ F[D(r)].

Since the δ-function is the identity operator for the convolution product, we ﬁnd,

after substitution of equation (2.84):

(q) =



D(q − g). (2.87)

The Fourier transform of the lattice potential of a ﬁnite crystal is, hence, described

by a similar formula as for the inﬁnite crystal, except that the reciprocal lattice

points now have a certain shape in reciprocal space. The exact shape of this volume

is determined by the external shape of the crystal. Let us consider two examples

of importance to electron microscopy: a planar thin foil, and a ﬁnite rectangular

crystal.

Example 2.5 Compute the reciprocal shape function D(q), also known as the shape

amplitude, for a thin foil of thickness z

with parallel top and bottom surfaces.

Answer: Taking the origin of the reference frame in the center of the foil, and the

z-direction normal to the foil, the reciprocal shape function is given by

D(q) =

+∞

−∞

−2πiq

+∞

−∞

−2πiq

−z

−2πiq

dz;

=−δ(q

)δ(q

)



−2πiq

2πiq



−z

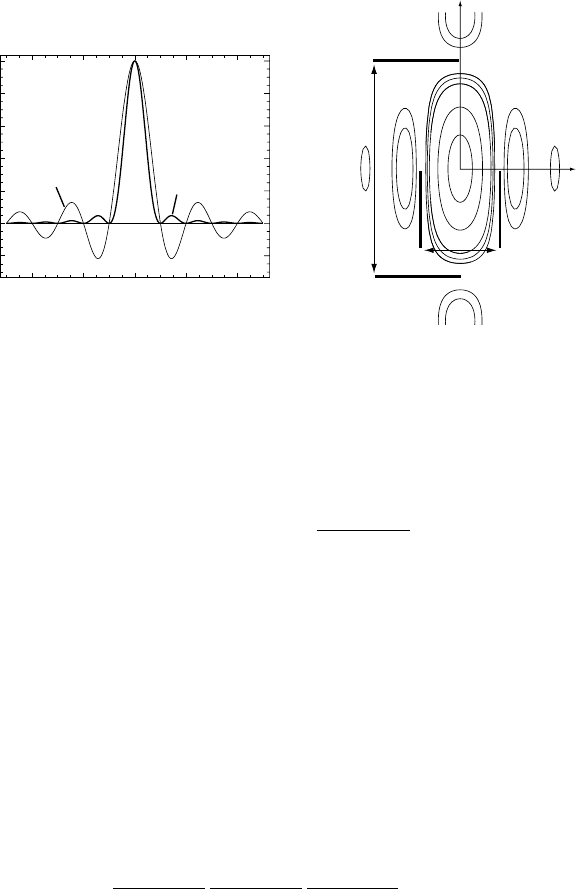
120 Basic quantum mechanics

-2π-4π 2π 4π

πq

1.0

0.8

0.6

0.4

0.2

0.0

-0.2

~1/A

~1/B

(a) (b)

Fig. 2.10. (a) Reciprocal shape functions D and D

for a thin foil of thickness z

along the

direction normal to the foil surface; (b) contour plot of a planar cut through

the reciprocal

shape function of a rectangular crystal D

, q

, 0).

which results in

D(q) = z

δ(q

)δ(q

)

sin(πq

)

πq

Fig. 2.10(a) shows the function D(0, 0, q

)/z

and its square.

Example 2.6 Compute the reciprocal shape function D(q) for a rectangular crystal

with dimensions A, B, and C.

Answer: Using the same reference frame as in the previous example, and carrying

out three identical integrations, we have

D(q) =

+A/2

−A/2

−2πiq

+B/2

−B/2

−2πiq

+C/2

−C/2

−2πiq

dz;

= ABC

sin(π Aq

)

π Aq

sin(π Bq

)

π Bq

sin(πCq

)

πCq

The square of this function is shown in Fig. 2.10(b) as a contour plot D

, q

, 0).

As we will see in the next chapter, nearly all TEM observations are carried

out with a circular electron beam; in other words, the illuminated volume in the

specimen is to a good approximation cylindrical with top and bottom surfaces not

necessarily ﬂat or parallel. Since the illuminated volume is always ﬁnite, but with

2.6 The electrostatic lattice potential 121

a diameter that depends on the beam diameter, the volume and shape of reciprocal

lattice points will vary with the incident beam “shape” and the shape function

D(r) is determined by the intersection of the incident beam and the specimen. For

typical thin foils used in TEM the third dimension (usually the z-axis) is much

smaller than the lateral dimensions (see the ﬁrst example above) and therefore the

reciprocal lattice points will be shaped as rods with their length axes perpendicular

to the foil. Since these rods reside in reciprocal space, they are called reciprocal

lattice rods or relrods.

We conclude from the examples above that, for a ﬁnite crystal, every reciprocal

lattice point is extended inﬁnitely in reciprocal space, but, because of the rapidly

decreasing character of these functions, each point can be approximated by a ﬁnite

volume in reciprocal space. The shape of this volume can become quite complicated

for samples which have a non-rectangular shape. In Section 9.8 on page 575 we

will discuss in detail how the shape amplitude D(q) for a polyhedral particle can

be calculated analytically.

Another important consequence of the ﬁniteness of a crystal is that the Bragg

condition for diffraction can be relaxed; whereas diffraction by an inﬁnite crystal

requires a mathematical point to coincide with the surface of the reﬂecting sphere

(a rather improbable event), diffraction by a ﬁnite crystal becomes more probable

because of the extent of the reciprocal lattice points.

2.6.4 The excitation error or deviation parameter s

Since diffraction is possible even when the Bragg relation is not precisely satisﬁed,

it is useful to have a parameter that measures the deviation from the exact Bragg

orientation. For a thin foil, the Fourier transform of the shape function can be

approximated by a relrod, as we have seen in the previous section. The deviation

from the exact Bragg orientation can then be measured as the distance between the

reciprocal lattice point and the Ewald sphere along the major axis of the relrod, or,

equivalently, along the foil normal. We represent this distance by a vector s = se

with e

the unit normal to the foil, pointing down towards the viewing screen of the

microscope such that k · e

is positive.

The length of the vector s can be computed as follows: from the equation for the

Ewald sphere (2.43) we have

(g + s) · (2k + g + s) = 0,

since the vector g + s ends on the Ewald sphere, by construction. This relation can

be rewritten as

2(k + g) · s + s

=−g · (2k + g); (2.88)

122 Basic quantum mechanics

we recognize the equation of the Ewald sphere on the right-hand side of this equa-

tion. If the angle between k + g and the foil normal is denoted by α, then we also

have

s +

2|k + g|cos α

−g · (2k + g)

2|k + g|cos α

≡ s

. (2.89)

We introduce

†

the new variable s

which is equal to the right-hand side of the

equation above; s

is known as the excitation error or the deviation parameter.Ithas

units of reciprocal distance, since it is measured in reciprocal space. For relativistic

electrons we have |k + g|≈|k|, which is of the order of several hundred nm

−1

(see Table 2.2); the second term on the left-hand side of equation (2.89) is thus

very small and can be safely ignored. The deviation parameter s

is then to a very

good approximation equal to the distance s between the reciprocal lattice point g

and the Ewald sphere, measured along the relrod. The difference between s

and

s increases with decreasing acceleration voltage and only becomes important for

low-energy electron diffraction.

According to Fig. 2.5(a), g · (2k + g) is negative when g is inside the Ewald

sphere, which means that the excitation error s

deﬁned in equation (2.89) is posi-

tive when the reciprocal lattice point g lies inside the Ewald sphere. s

is negative

when g lies outside the Ewald sphere, and is equal to zero when the Bragg orien-

tation is exactly satisﬁed. The deviation parameter is entirely determined by the

orientation of the crystal lattice with respect to the Ewald sphere, and is therefore

an experimental parameter. The microscope operator has full control over the mag-

nitude and sign of the deviation parameter. The degree to which s

can be varied

is determined by the type of specimen holder used for the observations; we will

discuss the major types of specimen holders in Section 3.9.2. The deviation param-

eter is one of the most important parameters for conventional TEM observations,

and, as we shall see in Chapters 6 and 8, the image contrast for both perfect and

defective crystals is to a large extent determined by the value of s

The excitation error can be computed numerically using the function

Calcsg in

the module

diffraction.f90. The function takes a g-vector, the incident wave vector

k, and the foil normal F as input, and returns the excitation error in nm

−1

2.6.5 Phenomenological treatment of absorption

In the preceding sections, we have only discussed elastic scattering processes, dur-

ing which the electron energy does not change. This is an approximation of what

†

The reason for selecting this particular expression will become clear in Chapter 5 where we will derive the

dynamical diffraction equations. The deviation parameter as deﬁned above appears directly in those equations.

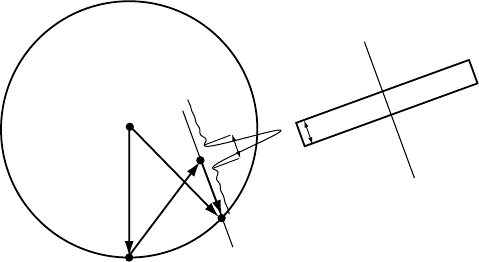
2.6 The electrostatic lattice potential 123

k' = k + g + s

Foil normal

2/t

Fig. 2.11. Deﬁnition of the excitation error in terms of the incident and diffracted wave

vectors and the reciprocal lattice vector g. The excitation error is measured along the normal

to the foil surface, or, equivalently, along the relrod. The angles between the v

ectors are

greatly exaggerated; in reality g is nearly perpendicular to k (for electron diffraction).

really happens when a beam electron interacts with the crystal. An electron can

exchange energy with the crystal in a variety of processes, which are commonly

grouped under the name inelastic scattering processes. Electrons that are inelasti-

cally scattered no longer travel in the directions predicted by the Bragg equation, and

give rise to a background image intensity, which reduces the contrast of the elastic

image.

The interaction between the beam electron and the crystal can be taken into

account by including the ground state and excited states of the crystal in the

Schr¨odinger equation. Following Yoshioka [Yos57], we write the Schr¨odinger equa-

tion as



T +

int



|=E

|, (2.90)

where

is the crystal Hamiltonian, and

int

is the electrostatic (Coulomb) in-

teraction term between the beam electron and the crystal. The wave function |

represents the state of the crystal and the beam electron, and can therefore be written

as the product of two wave functions:

|=



|ψ

|a

, (2.91)

where the functions |a

 represent the nth excited state of the crystal (|a

 is the

ground state). The beam electron wave function is given by |ψ

, for an electron

that leaves the crystal in the excited state |a

. The crystal wave functions |a

 are

the eigenfunctions of the crystal Hamiltonian

=

,

124 Basic quantum mechanics

where 

is the energy of the excited state. The crystal wave functions contain all

the information about lattice excitations, including phonons, plasmons, excitons,

polarons, and so on. The computation of the |a

 is therefore a non-trivial problem,

which lies at the heart of solid-state physics.

If we assume that the crystal wave functions and energies are known, then we

can substitute equation (2.91) into (2.90) and multiply the resulting equation by the

state a

|. Since a

=δ

for a complete set of functions, we ﬁnd



− 

−



|ψ

=



a

int

|ψ

≡



|ψ

, (2.92)

where we have introduced the matrix elements H

of the electrostatic interaction

between beam electron and crystal. These elements describe the probability am-

plitude that a beam electron will change the excitation state of the crystal from the

state |a

 to the state |a

. For elastic scattering, the crystal state does not change,

and, hence, the diagonal matrix elements H

describe elastic scattering processes.

Equation (2.92) is usually rewritten as a set of two equations, commonly known as

the Yoshioka equations [Yos57], by separating out the term m = 0:



− 

−

T − H



|ψ

=



n=0

|ψ

; (2.93)



− 

−

T − H



|ψ

=



n=m

|ψ

. (2.94)

In the absence of inelastic scattering, the off-diagonal matrix elements H

(m = n)

vanish, and the right-hand sides of both Yoshioka equations vanish. The diagonal

term on the left-hand side represents the interaction of the electron with the crystal,

and is commonly known as the potential energy of the beam electron in the crystal.

We have already seen that in the ground state of the crystal this potential energy is

given by H

= eV(r).

The computation of the matrix elements H

is a difﬁcult problem in general

and one usually approaches the computation of inelastic scattering probabilities by

only considering one effect at a time; e.g. the contribution of phonons, or plasmons,

and so on. Such computations are beyond the scope of this book. We refer to

Z.L. Wang’s book Elastic and Inelastic Scattering in Electron Diffraction and

Imaging for a recent review of inelastic scattering [Wan95]. We will instead use

the phenomenological approach of Moli`ere [Mol39] for x-ray diffraction, which

was ﬁrst applied to electron diffraction by Honjo and Mihama [HM54]; Yoshioka

[Yos57] showed formally that inelastic scattering in electron diffraction can be

taken into account by adding a complex potential W (r) to the electrostatic lattice

potential. The imaginary part of this potential describes the inelastic scattering

processes in the form of an attenuation of the wave amplitude (absorption); the real

2.6 The electrostatic lattice potential 125

part of W (r) is associated with virtual inelastic scattering and has been shown by

P. Rez [Rez78] to be small for high-energy electrons. We will hence assume that

the so-called optical potential W (r) is purely imaginary and of the form iW (r).

Next, we show that such an imaginary term can describe absorption: following

[GBA66] we have

V (r) → V

(r) = V (r) + iW (r). (2.95)

Now consider the time-dependent Schr¨odinger equation:

i h

∂

∂t

=−

 − eV

, (2.96)

where V

is the complex lattice potential deﬁned in equation (2.95). The complex

conjugate of this equation is given by

−i h

∂

∗

∂t

=−



∗

− eV

∗



∗

. (2.97)

Multiplying the ﬁrst equation by 

∗

, the second by , and subtracting the second

from the ﬁrst results in

i h

∂

∗

∂t

=−

(

∗

 − 

∗

) − e



− V

∗





∗

. (2.98)

This in turn can be rewritten as

∂

∗

∂t

−

i h

∇·(

∗

∇ − ∇

∗

) =



− V

∗





∗

. (2.99)

Since 

∗

= ρ equals the probability density and the argument of the divergence

operator is the electron ﬂux J,

†

we can rewrite this equation one more time (using

equation 2.95):

∂ρ

∂t

+∇·J =−

Wρ. (2.100)

We thus ﬁnd that, if W > 0, then the total number of electrons will decrease with

time, i.e. absorption will occur. If W = 0, then equation (2.100) reduces to a stan-

dard continuity equation for the probability density. Note that this description does

not contain any details concerning the exact nature of the inelastic scattering pro-

cess; all that is required to describe absorption is the positive imaginary part of the

lattice potential.

For the remainder of this book we will use the phenomenological description of

absorption and inelastic scattering contributions.

†

See, for instance, [LL74].

126 Basic quantum mechanics

2.6.6 Atomic vibrations and the electrostatic lattice potential

The derivation of the atomic scattering factor f

(s) assumed that the atom was at

rest at the origin of the reference frame. In reality, atoms vibrate around their equi-

librium lattice positions, and the amplitude of this vibration depends on the absolute

temperature. The theory of lattice vibrations (or phonons) is well developed, and

we refer the reader to [Bir84] for a detailed discussion of lattice dynamics.

Lattice vibration frequencies for most solids are in the range 10

–10

Hz.

A 200 keV electron travels at a velocity of v = 0.695c, which corresponds to a

distance of about 208

µmina10

−12

s time interval. This is very large compared to

the atomic dimensions, which means that subsequent electrons will “see” this atom

located at different positions, but essentially at rest for each individual electron.

Each atom, therefore, appears to be spread out over a larger volume and this affects

the electron scattering factor f

(s). The correction factor is commonly known

as the Debye–Waller factor, and we will next derive an explicit expression based

on the deﬁnition of the atomic scattering factor.

Consider an isolated atom at rest at the origin, with atomic potential V

(r). The

atomic scattering factor f

(s) expresses the probability amplitude that an incident

electron with wave vector k will be scattered by the atom in the direction k



; this is

expressed by the bra-ket:

(k) =

2πik



·r

(r)

2πik·r

Assume next that the atom vibrates around this equilibrium position with a vibration

amplitude u(t). For simplicity and without loss of generality we will assume that

the vibration occurs along the x-direction. The instantaneous atomic potential at a

time t is given by

(r, t) = V

(r + u(t)) = V

(r + u(t)e

For small vibration amplitudes the instantaneous potential can be expanded in a

Taylor series in u, as follows (dropping the argument r):

(t) = V

u(t)

u=0

u(t)

u=0

+····

If we average this expression over time, then all odd powers of u(t) will vanish,

since positive and negative excursions are equally likely over a sufﬁciently long

time interval. Denoting the time average by ,wehave

(t)

= V

u



u=0

+····

2.6 The electrostatic lattice potential 127

Next, we can calculate how the atomic scattering factor is modiﬁed by this average

potential:

(k)

2πik



·r

(t)

2πik·r

;

...

−2πik·r



u=0

+···



dr;

1 + (2π ik)

+···

...

−2πik·r

dr;

≈ e

−2π

u

(k)

(k),

where we have used the relation F

f (x)/dx

] = (2πiu)

f (u) (e.g. see [Cow81,

p. 32]). Introducing |k|=2s as before we arrive at the time-averaged atomic

scattering factor:

 f

(s)= f

(s)e

−8π

u

s

= f

(s)e

−Bs

; (2.101)

the symbol B is proportional to the atomic mean-square vibration amplitude u

,

which is expressed in units of nm

and depends on absolute temperature. For

realistic simulations, the Debye–Waller factor must be taken into account. We

have assumed in this simpliﬁed derivation that the vibrations are isotropic. For

anisotropic vibrations B becomes a second-rank tensor, which can be represented

by a “vibrational ellipsoid”. The mean-square vibration amplitude then depends on

the particular reciprocal lattice vector g selected for the computation of f

(s).

The Debye–Waller factor B is a function of temperature B = B(T ); exact ex-

pressions for B can be derived for a given vibration model, and for details we refer

to the International Tables for Crystallography, volume C [Shm96], and references

therein. Note that B does not vanish at 0 K because of the zero-point motion of the

atoms.

For elemental solids, the Debye–Waller factor can be calculated from the phonon

density of states g(ω), using the following relation:

B(T ) =

4π

coth





g(ω)



dω,

where m is the atomic mass, T is the temperature (in kelvin), k

is the Boltzmann

constant, and ω

is the maximum phonon frequency. The phonon density of states

can be measured experimentally using neutron diffraction techniques. This relation

has been used by Gao and Peng [GP99] to parameterize the Debye–Waller factors

for 68 elemental crystals and a number of compounds in the temperature range

from T = 0 to 1000 K. The dashed lines in Fig. 2.9 represent the atomic scattering