Graef M. Introduction to conventional transmission electron microscopy
Подождите немного. Документ загружается.

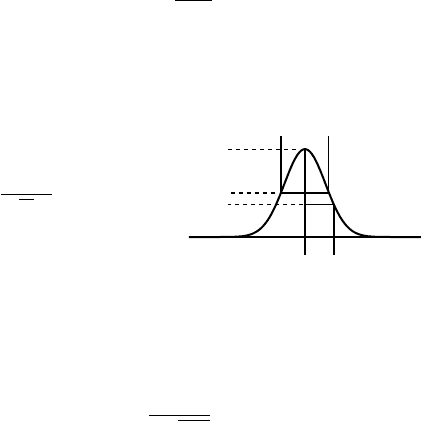
608 Phase contrast microscopy
10.2.2.1 Derivation of the damping envelope
The coherent TCC in equation (10.38) is defined by the product
T
coh
cc
(q, q
) ≡ T (q)T
∗
(q
) = A(q)A(q
)e
−i[χ(q)−χ(q
)]
, (10.39)
where we have used the explicit form of the transfer function in terms of the aperture
function and the aberration function. In the case of partial coherence, there is a range
of incident beam directions and also a range of beam energies which must be taken
into account. We will denote by s(q) the normalized source spread function which
for a Gaussian distribution is given by
s(q) ≡
1
πq
2
0
e
−(q/q
0
)
2
. (10.40)
Similarly, we can define the defocus spread function f ( f ) by the Gaussian
distribution
f ( f ) ≡
1
√
π
e
−( f /)
2
.
1
1/2
δ
∆
1/e
(10.41)
The quantities q
0
and are the e
−1
half-width values of the Gaussian distributions,
as indicated in the figure. The full width at half maximum (FWHM) value δ is
related to as follows:
=
δ
2
√
ln2
≈ 0.60δ. (10.42)
For partial coherence, the TCC in equation (10.39) must be replaced by an integra-
tion over both spread functions:
T
pc
cc
(q, q
; f ) =
..
s(q
) f ( f
)T
coh
cc
(q
+ q, q
+ q
; f + f
)dq
d f
,
(10.43)
where we have explicitly written the defocus dependence of the transfer functions.
The image intensity can then be computed by substituting this integral into equa-
tion (10.38). This integral is not trivial and the reader is referred to the following
sources for a more detailed computation: Frank [Fra73], Ishizuka [Ish80], and
Kirkland [Kir98]. We will compute an approximate expression for the integral by
considering the spread functions one at a time.

10.2 The microscope as an information channel 609
We will assume that the exit wave function ψ(r) can be written in the following
form [Fra73]:
ψ(r) = 1 + O(r),
such that
ψ(q) = δ(q) + O(q).
Substituting ψ into equation (10.38) and working out the integrations leads to
I (q) =
.
T
cc
(q
, q
+ q)[δ(q
) + O(q
)][δ(q
+ q) + O
∗
(q
+ q)] dq
;
= T
cc
(0, q)δ(q)
+ [T
cc
(0, q)O
∗
(q) + T
cc
(−q, 0)O(−q)]
+
.
T
cc
(q
, q
+ q)O(q
)O
∗
(q
+ q)dq
. (10.44)
The first term describes the background intensity; the second term is the linear
term since it only depends on a single spatial frequency vector q. The last term is
the non-linear component of the image. We will first consider the linear term and
determine how it is affected by the presence of the defocus spread function f ( f ).
From the definition of the partially coherent TCC we have
T
cc
(−q, 0) =
.
f ( f
)T
coh
cc
(−q, 0; f + f
)d f
;
T
cc
(0, q) =
.
f ( f
)T
coh
cc
(0, q; f + f
)d f
= T
∗
cc
(−q, 0).
The explicit computation of T
cc
(−q, 0) for the defocus spread proceeds as follows:
after substitution of the transfer function and replacing −q by q we have
T
cc
(q, 0) =
.
f ( f
)A(q)e
−iχ(q; f + f
)
d f
. (10.45)
Since the defocus spread function is strongly peaked around its central value, we
can expand the function in the exponential in a Taylor expansion with respect to
f and keep only the linear term:
χ(q; f + f
) ≈ χ(q; f ) + f
∂χ
∂f
+···. (10.46)
For all vectors q inside the aperture we have
T
cc
(q, 0) =
e
−iχ(q; f )
√
π
.
e
−( f
/)
2
e
−i f
∂χ/∂f
d f
. (10.47)

610 Phase contrast microscopy
The derivative is calculated easily as
∂χ
∂f
=
∂
∂f
π
C
s
2
λ
3
q
4
− λ fq
2
=−πλq
2
.
Substituting in equation (10.47) and using the following standard integral
F[e
−x
2
] =
√
πe
−π
2
q
2
we arrive at
T
cc
(q, 0) = e
−iχ(q)
e
−π
2
(λq
2
)
2
/2
= e
−iχ(q)
e
−π
2
(δλq
2
)
2
/16 ln 2
≡ e
−iχ(q)
E
t
(q). (10.48)
The function E
t
(q) is known as the temporal incoherence envelope function.Itis
an exponential damping function which depends on the magnitude of the defocus
spread , but is independent of the actual defocus value.
By assuming that the defocus spread function is sharply peaked, we have been
able to write the cross coefficient as a simple multiplication by an exponential
damping factor. We can repeat this exercise for the source spread function (10.40),
and work out the following integral:
T
cc
(q, 0) =
.
s(q
)A(q
+ q)A(q
)e
−i
[
χ(q
+q)−χ(q
)
]
d f
. (10.49)
Using a Taylor expansion for small q
we find:
χ(q + q
) ≈ χ(q) + q
·∇χ(q) +···.
Working through the integration as before we find for the TCC:
T
cc
(q, 0) = e
−iχ(q)
e
−
1
4
q
2
0
|∇χ |
2
≡ e
−iχ(q)
E
s
(q). (10.50)
The function E
s
(q) is known as the spatial incoherence envelope function.Itis
again an exponential damping function which depends on the magnitude of the
gradient of the aberration function |∇χ|. This gradient is given explicitly by
∇χ(q) = 2π
C
s
λ
3
q
2
− λ f
q. (10.51)
The gradient becomes large for the higher spatial frequencies, as is obvious from
Fig. 10.4, and depends on the defocus. The explicit expression for E
s
is then
given by
E
s
(q) = e
−π
2
q
2
0
(
C
s
λ
3
q
3
−λ fq
)
2
. (10.52)
The evaluation of the integral (10.43) for both defocus spread and source spread
functions simultaneously is rather lengthy and we refer to Ishizuka [Ish80] and
Kirkland [Kir98] for a detailed derivation. The primary complication stems from
the fact that the Taylor expansion of the aberration function must now be carried
out with respect to both q
and f
, and all terms linear in either of these quantities

10.2 The microscope as an information channel 611
must be kept, resulting in the following expansion:
χ(q + q
,f + f
) ≈ χ(q,f ) + f
∂χ
∂f
+ q
·∇χ(q)
+ f
q
·
∂
2
χ
∂q
∂f
+···.
The last terms couples the effects of both spread functions. For completeness we
provide the partially coherent microscope transfer function in the presence of de-
focus and source spread:
T (q) = A(q)e
−iχ(q)
E
s
(q)E
t
(q);
= A(q)e
−iχ(q)
exp
−
(πλ)
2
2u
q
4
exp
−
π
2
θ
2
c
λ
2
u
C
s
λ
3
q
3
− f λq
2
,
(10.53)
where
u = 1 + 2(πθ
c
)
2
q
2
,
and the beam divergence angle θ
c
is related to q
0
by
θ
c
= λq
0
.
Equation (10.53) partially accounts for the effects of incoherence. While it is not
exact, it is a useful expression since the temporal and spatial envelope functions
appear in the form of multiplicative factors. For the exact case, we would need to
numerically integrate equation (10.43) without applying the Taylor expansions for
the aberration function.
To wrap things up, we substitute the function T (q) into equation (10.44) to
determine the linear part of the image intensity. Using O(q) = O
r
(q) + iO
i
(q) and
the fact that O
r,i
(q) = O
∗
r,i
(−q) (Friedel’s law) we have [Fra73]:
I
linear
(q) = T (q)O
∗
(q) + T (−q)O(−q);
= O
r
(q)[T (q) + T (−q)] + iO
i
[T (−q) − T (q)];
= 2A(q)E
s
(q)E
t
(q)
[
O
r
(q) cos χ (q) + O
i
(q) sin χ (q)
]
. (10.54)
This expression clearly shows that the real and imaginary parts of the exit wave
function (or, equivalently, the phase and amplitude) are mixed by the coherent
microscope transfer function and attenuated by the incoherent envelope functions.
The non-linear component of equation (10.44) is more complicated to compute. For
crystalline samples the integration can be replaced by a summation over reciprocal
lattice vectors.
612 Phase contrast microscopy
10.2.2.2 Significance of the damping envelope
After the lengthy derivations of the previous section, we are now ready to deter-
mine how the partially coherent transfer function is different from the coherent
transfer function. As before, we can introduce dimensionless quantities based on
equations (10.10) and (10.11) and the envelope function becomes (taking u = 1):
E
s
(Q)E
t
(Q) = exp
6
−
π
2
2
$
¯
2
Q
4
+ 2
¯
q
2
0
(Q
3
− DQ)
2
%
>
, (10.55)
with
¯
=
√
C
s
λ
,
and
¯
q
0
= q
0
(C
s
λ
3
)
1/4
.
Figure 10.11 shows the total envelope function E
s
E
t
for several combinations of
dimensionless parameters. In the top half of the figure
¯
q
0
= 0.05, and the solid
lines indicate the defocus values D = 1, 2, 3, and 4. In the bottom half
¯
q
0
= 0.1.
The dash-dotted line is the temporal incoherence envelope E
t
for
¯
= 0.1 and
¯
q
0
= 0.0. The curves in this figure reveal that the temporal incoherence envelope
0.0
1.0
0.5
-0.5
-1.0
0123
Dimensionless Frequency Q
Damping Envelope
temporal incoherence
envelope (∆ = 0.1)
q
0
= 0.05
q
0
= 0.1
D=1
2
3
4
1
2
3
4
Fig. 10.11. Incoherent damping envelope for a few selected values of the dimensionless
parameters
¯
and
¯
q
0
and several values of D.

10.2 The microscope as an information channel 613
-101234
0
1
2
3
Dimensionless Frequency Q
Dimensionless Defocus D
01234
(a)
(b)
Fig. 10.12. Incoherent damping envelope E
s
E
t
for
¯
= 0.1 and
¯
q
0
= 0.1 shown as a
grayscale plot
(left) and multiplied by sin
χ(q) (right).
is a smoothly varying function whereas the spatial incoherence envelope shows a
single “dip” around Q = 1.
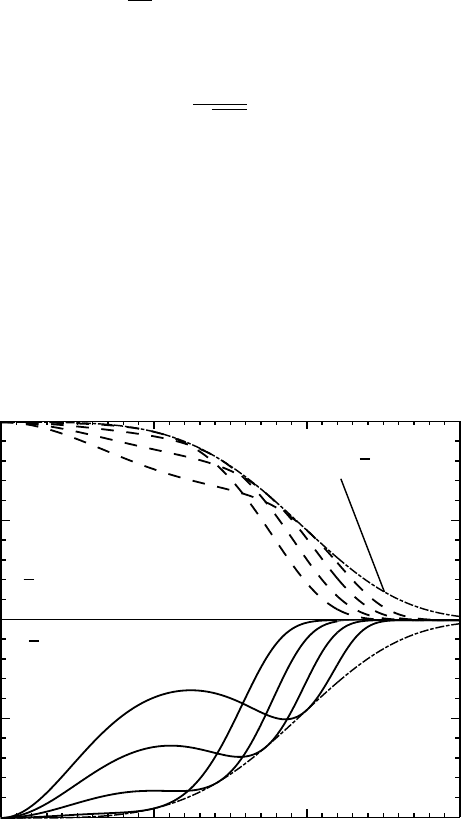
Alternatively, we can represent the damping envelope by a grayscale plot, similar
to that of Fig. 10.7. This is shown in Fig. 10.12(a) for
¯
= 0.1 and
¯
q
0
= 0.1. The
product of sin χ(Q) and E
s
(Q)E
t
(Q) is shown in Fig. 10.12(b); comparison with
Fig. 10.7 reveals that the higher-frequency oscillations are strongly damped, and
that the point where damping becomes severe moves to larger Q with increasing de-
focus D. This is a consequence of the defocus dependence of the spatial incoherence
envelope. The dashed line in Fig. 10.12(b) represents the Scherzer frequency
Q = 6
1/4
.
Vertical sections through Fig. 10.12 at the defocus values corresponding to the
first four passbands D
n
are shown in Fig. 10.13. Several trends can be observed
from this figure:
r
the width of the passband decreases with increasing order n;
r
the number of oscillations of sin χ(Q) before the passband is equal to the order of the
passband;
r
the cutoff frequency of the incoherent envelope function shifts to larger spatial frequencies
with increasing defocus D.
Beyond a certain spatial frequency Q, the incoherent damping envelope becomes
so small that virtually no signal can be passed through. It is therefore useful to
define a parameter which indicates the frequency beyond which no further signal
information can be passed through the lens. This point is known as the information
limit.

614 Phase contrast microscopy
1
0
-1
1
0
-1
01230123
n= 0
D=1.2247
n= 1
D=2.3452
n= 2
D=3.0822
n= 3
D=3.6742
QQ
sinχ(Q)E
s
(Q)E
t
(Q)
Q
S
Fig. 10.13. Vertical sections through the function sin χ E
s
E
t
for the first four passbands
D =
√
(8n + 3)/2. The Scherzer spatial frequency Q
S
is indicated for n = 0.
We should point out that the above derivation assumes that defocus and spheri-
cal aberration are the only relevant lens aberrations, and that two-fold astigmatism
has been properly corrected. If additional aberrations are to be taken into account
(say, three-fold astigmatism and axial coma), then the expression for the aberra-
tion function becomes more complicated and so will the spatial incoherence en-
velope, since E
s
depends on the gradient ∇χ. The spatial incoherence envelope
must therefore be recomputed every time a new aberration is taken into account
[KS95].
The damping envelope attenuates the signal frequencies and at some point the
product of the signal and the damping envelope will fall below the noise level of
the signal. If we define the signal-to-noise ratio as s ≡ S/N, then we can introduce
the information limit due to the damping envelope E by determining at which
spatial frequency SE(q) = N ,orE(Q) = 1/s. Each damping envelope will have
a characteristic frequency Q
i
for which this equality is true.
r
Temporal incoherence envelope. The function E
t
(Q) reaches the value 1/s at
Q
i
=
√
2lns
π
¯
1/2
.
Converting the dimensionless quantities we find
q
i
=
√
2lns
πλ
1/2
.
10.2 The microscope as an information channel 615
0123
D = -2
0
6.75
13.5
20
10
0
-10
-20
Q
χ/2π
∆
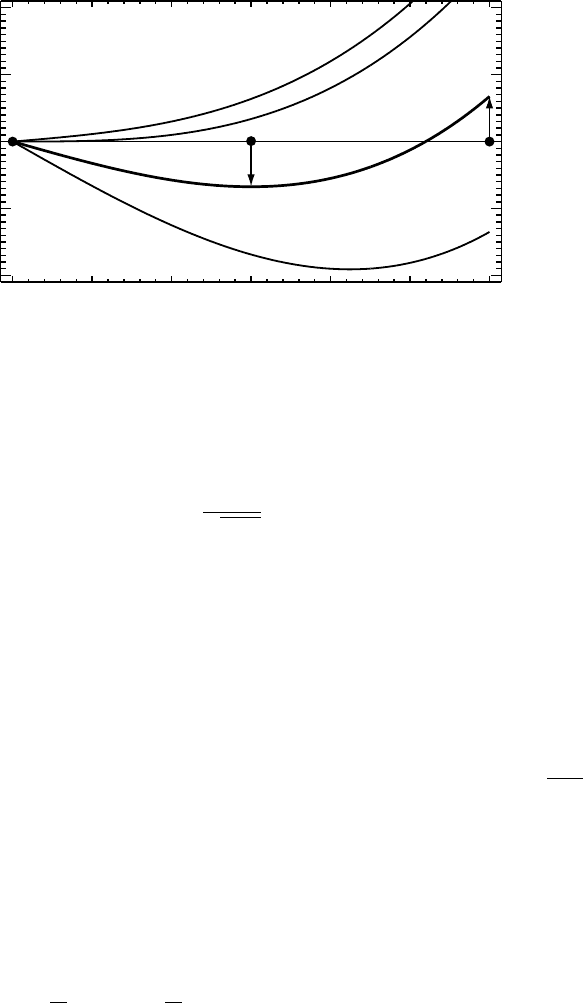
Fig. 10.14. Illustration of the defocus dependence
of the gradient of the aberration function
χ(Q).
The spatial distance corresponding to q
i
is commonly denoted by ρ
c
and is known as the
chromatic information limit:
†
ρ
c
≡
πλ
√
2lns
1/2
. (10.56)
r
Spatial incoherence envelope. The function E
s
(Q) is a bit more complicated than E
t
(Q),
since its argument also depends on the defocus value D. The spatial incoherence envelope
will have a minimal effect if the argument of the exponential varies as little as possible
across the frequency range of interest. This means that we must look for the defocus
value for which ∇χ has a minimum variation over the interval [0, Q
max
]. Figure 10.14
shows the function ∇χ/2π = Q
3
− DQ for the frequency range Q = [0, 3] and for
several values of D. For over-focus conditions (D < 0) the gradient varies substan-
tially across the interval [0, 3] and the only minimum occurs at Q = 0. For under-focus
conditions (D > 0) the gradient
has a minimum located at the value
Q
min
=
√
D/3
(exercise).
We will now determine the defocus value for which the value of ∇χ at the minimum
is equal to the negative of the value at Q
max
, i.e. [Lic91]:
∇χ(Q
min
) =−∇χ (Q
max
),
which translates into
D
3
3/2
− D
D
3
1/2
=−
Q
3
max
− DQ
max
.
†
“Chromatic” because the temporal incoherence envelope deals with the energy spread of the electron
beam.
616 Phase contrast microscopy
This is a third-order polynomial equation in D which has three solutions (e.g. [AS77]):
D
1
=
3
4
Q
2
max
and D
2,3
= 3Q
2
max
. Only D
1
corresponds to a minimum within the range
[0, Q
max
]; the other value corresponds to the minimum at Q = Q
max
. The defocus value
D for which the function ∇χ (Q) is minimized over the interval [0, Q
max
] is known as the
optimum focus or the Lichte focus, after H. Lichte who first introduced it in the context
of electron holography [Lic91].
Converting from dimensionless quantities we find for the optimum defocus:
f
opt
=
3
4
C
s
λ
2
q
2
max
. (10.57)
At the optimum defocus and near the maximum spatial frequency the spatial incoherence
envelope can be rewritten as
E
s
(Q
max
) = e
−π
2
¯
q
2
0
1
16
Q
6
max
= e
−π
2
¯
q
2
0
a
2
Q
6
max
,
where we have introduced
the variable
a
2
=
1
16
. At the optimum defocus a =
1
4
;itis
easy to show that at Gaussian defocus (D = 0) we have a = 1. The effect of the spatial
incoherence envelope at the optimum focus is therefore smaller than the effect at the
Gaussian defocus.
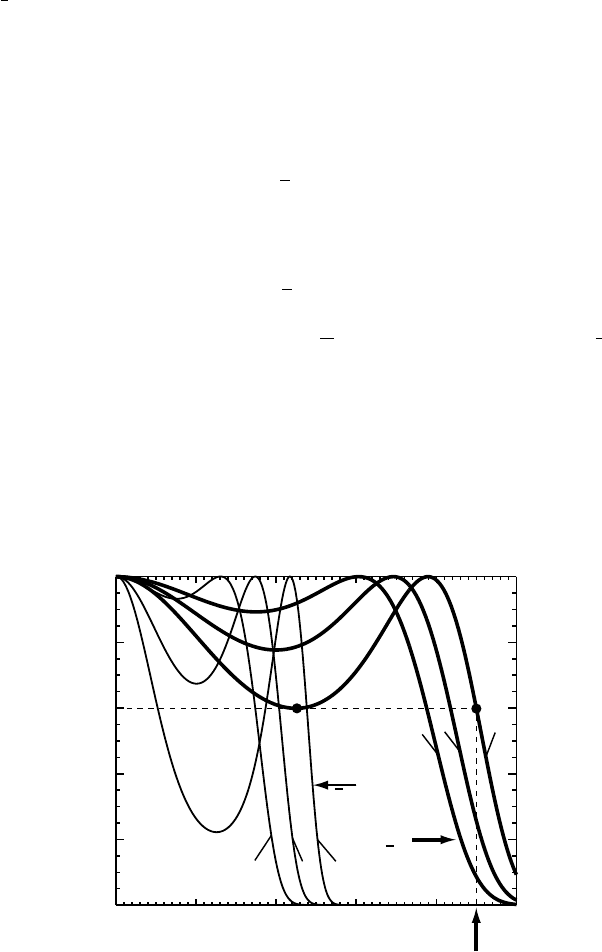
Figure 10.15 shows the spatial incoherence envelope at optimum defocus for two
different electron sources: a thermionic LaB
6
source with
¯
q
0
= 0.1, and a field emission
source with
¯
q
0
= 0.01. Since the field emission source has a much smaller beam diver-
gence angle θ
c
(which is essentially the meaning of
¯
q
0
), the envelope extends to larger
1.0
0.8
0.6
0.4
0.2
0.0
012345
Q
E
s
(Q) at optimum focus
Q
max
= 1.5 2 2.5
Q
max
= 3.5 4 4.5
q
0
= 0.1
q
0
= 0.01
Q
max
= 4.5
Fig. 10.15. Spatial incoherence envelope at the optimum defocus for two different source
spread parameters
¯
q
0
typical for a LaB
6
source (0.1) and a field emission source (0.01). For
each source spread three different values of Q
max
are shown. The dashed line indicates that
the value of the envelope at Q
max
is equal to the value at the lowest point of the dip.

10.2 The microscope as an information channel 617
spatial frequencies than that of the thermionic source. For each source three different
values of Q
max
are shown. The dashed lines on the Q
max
= 4.5 curve indicate that the
value of E
s
(Q)atQ
max
is equal to the value at the minimum of the dip, which is located at
Q
max
/2.
The spatial incoherence envelope is equal to the inverse of the signal-to-noise ratio s
when the following relation is satisfied:
ln s = π
2
¯
q
2
0
a
2
Q
6
=
πaθ
c
λ
2
C
2
s
λ
6
q
6
,
where we have replaced all dimensionless quantities. From expression (10.32) we derive
that C
2
s
λ
6
= 36ρ
8
S
. Rearranging terms, we find the following expression for the spatial
incoherence information limit:
ρ
θ
c
≡
6πaθ
c
λ
√
ln s
ρ
4
S
1/3
. (10.58)
Before we analyze representative values of the two information limits introduced
in this section we will first discuss three additional envelope
functions which may
have an effect on the information limit.
10.2.2.3 Additional envelope functions
There are three additional envelope functions which can suppress the higher spatial
frequencies (following de Jong and Van Dyck [dJVD93]).
(i) Sample drift. If the sample moves with a constant velocity v
d
in a given direction,
†
then the total sample displacement during the exposure time t
e
is given by the vector
d = v
d
t
e
. Only lattice planes that contain the drift direction are unaffected, which can
be expressed by the dot product between the reciprocal lattice vector (the plane normal)
and the drift vector. It can be shown (see Frank [Fra69]) that the resulting damping
envelope is described by the function
E
d
(q) =
sin(πq · d)
πq · d
≈ e
−
1
6
(πq·d)
, (10.59)
from which we can derive a drift information limit (using the exponential
approximation):
ρ
d
≡
πd
√
6lns
. (10.60)
(ii) Sample vibration. If the sample vibrates with an amplitude u and a frequency which is
significantly higher than the inverse of the exposure time t
e
, then it can be shown [Fra69]
†
Sample drift is most probably due to thermal instabilities in the microscope or microscope room. Small temper-
ature gradients in the room or column may cause the sample holder to drift at several hundredths of a nanometer
per second. Thermal equilibrium is essential to minimize the effects of sample drift.
