Graef M. Introduction to conventional transmission electron microscopy

Подождите немного. Документ загружается.

638 Phase contrast microscopy

(a) (b) (c)

220 @ 6.9 nm

-1

8.4 nm

-1

6.4 nm

-1

Fig. 10.29. (a) Diffractogram of the sum of two micrographs with a small relative translation,

showing Young fringes; (b) Fourier ﬁltered image using only the Young fringe periodicity;

the Young fringes are no longer detectable.

equation (10.58) on page 617 and requires a series of image pairs for increasing

defocus. An alternative method for the determination of the effective source size,

which is related to the damping envelope, can be found in [HSI91]. A full and accu-

rate characterization of all electron optical parameters is essential if the information

content of an image or series of images is to be pushed towards the information

limit. The reader is referred to volume 64 of the journal Ultramicroscopy for a series

of papers related to the acquisition of images with an information limit of 0.1 nm.

That it is possible to push the information limit well below 0.1 nm has been shown

by O’Keefe and coworkers [OHW

01,ONWA01] in the One

Angstrom Microscope

project (OAM) at the Lawrence Berkeley Laboratory.

10.3 High-resolution image simulations

We have all the ingredients necessary for a HREM image simulation: the exit

wave (from the

BWEW.f90 program), and the microscope contrast transfer function

(computed via the

ctf.f90 module). The computation of a single high-resolution

image, using the linear image formation model, is now straightforward and consists

of the following steps:

for a given exit wave φ(r), compute its Fourier transform φ(q);

compute the transfer function T (q) for a given set of microscope parameters;

multiply φ(q) and T (q), and apply the aperture mask;

inverse Fourier transform φ(q)T (q) to the image plane and take the modulus-squared to

convert to intensities.

There are obviously many parameters which can be varied: defocus, defocus

spread, beam divergence, foil thickness, acceleration voltage, and so on. In ad-

dition, the residual aberrations discussed in Section 10.2.5 can also be included

10.3 High-resolution image simulations 639

0 102030405060708090100

∆f

[010]

[001]

Fig. 10.30. HREM image simulation for the [100] zone axis of BaTiO

, using the electron

optical parameters stated in the text. The exit wave computation was carried out with the

BWEW.f90 program, and the images were simulated with HREMExample.f90. All images use

a common intensity scale.

in the simulations. Typically, however, only two parameters are changed: the foil

thickness and the microscope defocus. The resulting images are assembled in a ma-

trix of through-focus series, similar to the one shown in Fig. 10.30. The simulations

were carried out for the [100] zone axis orientation of BaTiO

, using 400 kV elec-

trons and a sampling grid of 32 × 32 pixels. The maximum |g| included in the exit

wave computation is 35 nm

−1

, resulting in a 615-beam Bloch wave computation

(

BWEW.f90

). The exit waves were computed for 10 foil thicknesses from 2 to 20 nm.

The

HREMExample.f90 program implements the steps outlined above. The program

uses a namelist ﬁle to store the electron optical parameters for a given microscope.

The following parameters were used for Fig. 10.30: C

= 1 mm, θ

= 0.8 mrad,

 = 8 nm, and the aperture radius is 6 nm

−1

. Underfocus values from f = 0to

100 nm were used.

Comparison of the simulated images with the projected structure model to the

left of Fig. 10.30 shows that for most thickness–defocus combinations, the image

consists of bright or dark contrast at the metal atom positions (Ba or Ti). In some

cases, the O positions also show bright or dark contrast. The Scherzer point res-

olution (at  f

= 49.7 nm) is 0.165 nm, so that the (020) and (002) interplanar

640 Phase contrast microscopy

2.49 2.55

3.60 5.20 6.00

Aperture Radius (nm

-1

)

Thickness (nm)

5 nm

-1

010

001

2.49

2.55

3.60

5.20 6.00

011 021

Fig. 10.31. Inﬂuence of the aperture size on simulated HREM images, for ﬁve different

aperture sizes indicated on the BaTiO

[100] zone axis pattern. See the text for more details.

spacings can be resolved directly. It is also clear from the images that the bright or

dark features do not always coincide with the projected atom positions.

Figure 10.31 illustrates the effect of the diffraction aperture. The aperture radii

were selected so that only selected reﬂections contribute to the image. The small-

est aperture, with a radius of 2.49 nm

−1

, only admits the {001} reﬂections, and

the resulting image consists of a sinusoidal modulation with the d

001

spacing as

wavelength. A slightly larger aperture allows the {010} reﬂections to contribute as

well, and the fringe pattern becomes two dimensional. The strong reﬂections of the

{011} family are admitted with the 3.6nm

−1

aperture, and the image contrast in-

creases signiﬁcantly. Larger apertures then admit the {021}and the {020}and {002}

families. Since the chromatic information limit for the selected set of parameters

is ρ

= 0.144 nm, there is no point in using an aperture larger than the inverse of

this limit. No further image details would be introduced by such a larger aperture.

The

HREMExample.f90 program is provided on the website as an example of how

high-resolution image simulations can be performed. The reader is encouraged to

adapt the program, for instance to include non-rectangular projected unit cells.

There are several other HREM simulation programs available, including:

NCEMSS: developed at Lawrence Berkeley Laboratories, runs on various UNIX plat-

forms, ncem.lbl.gov/frames/software.htm;

EMS: developed at the Ecole Polytechnique F´ed´erale de Lausanne, runs on most plat-

forms, cimesg1.epfl.ch/CIOL/ems.html, [Sta87];

ACEM: programs developed by E.J. Kirkland as part of the book on Advanced Computing

in Electron Microscopy, [Kir98];

MacTempas: developed by R. Kilaas, runs on the Macintosh platform,

www.totalresolution.com.

10.4 Lorentz image simulations 641

There are many other packages available and the reader is encouraged to search

on the web for commercial, shareware and free software. Details on simulation

methods can be found in [Kir98,KO89, BCE88, Spe88].

10.4 Lorentz image simulations

In Section 7.5.3, we have seen that a magnetic thin foil affects only the phase of

the electron wave, and not its amplitude. Lorentz microscopy is, therefore, a phase

contrast method, and the magnetic object is a strong phase object. The phase shift

can easily be several radians large so that the weak phase object approximation of

Section 10.2.1.3 is of little or no use for Lorentz microscopy. It is possible, however,

to simplify the microscope transfer function derived earlier in this chapter. The

Lorentz deﬂection angle θ

is of the order of a few µrad, and hence the relevant

spatial frequency vectors q are short vectors. This, in turn, means that the dominant

terms in the phase transfer function are the lowest-order terms in q, which are

the quadratic and fourth-order terms. The contrast transfer function (10.53) can be

rewritten by grouping terms of order q

and q

, putting u = 1, and ignoring all

higher-order terms:

(q) = A(q − q

(10.73)

with

=−

(

πθ

 f

)

+ iπλ

[

 f + C

cos 2(φ − φ

)

]

;

=−

(

πλ

)

+ 2

(

πθ

)

 fC

− i

We have included two-fold astigmatism as a component of the transfer function.

From the aberrated wave function in the back focal plane, the image intensity can

be derived by an inverse Fourier transform:

I (r) =|F

−1

[ψ(q)]|

=|ψ (r) ⊗ T

(r)|

, (10.74)

where ⊗indicates the convolution product and the function T

(r)isthepoint spread

function appropriate for Lorentz microscopy.

One might wonder whether or not spherical aberration, the most important lens

aberration for most observation modes, is still important. It turns out that we can

safely ignore the phase shifts caused by spherical aberration, as illustrated by the

following example: at 400 kV, a sample with saturation induction of B

= 1 tesla,

and thickness t = 100 nm will give rise to a Lorentz deﬂection angle of eB

λt/ h =

µrad. This angle corresponds to a spatial frequency of q = λθ

= 0.024 nm

−1

The phase shift caused by spherical aberration (C

in meters) at this spatial frequency

is then equal to φ = 2.44 × 10

−6

. This phase shift remains smaller than 1 mrad

642 Phase contrast microscopy

for spherical aberration constants of up to 409 m. Since the spherical aberration

of a dedicated Lorentz pole piece is still signiﬁcantly smaller than several hundred

meters, it is safe to simply ignore phase shifts caused by C

in all Lorentz image

simulations. This means that z

is effectively a real number.

For an in-focus image ( f = 0) the ﬁrst term of z

becomes the leading compo-

nent of the damping envelope, so we must take it into account for all Lorentz image

simulations. The defocus spread  is signiﬁcantly larger for Lorentz microscopy

when a dedicated Lorentz pole piece is used. The chromatic aberration constant C

of such a lens is in the range of meters rather than millimeters, similar to the spher-

ical aberration constant. We cannot ignore this damping factor, since for  f = 0,

ignoring  would amount to ignoring the complete damping envelope.

A Lorentz image simulation proceeds along the same lines as a high-resolution

simulation: ﬁrst we must compute the phase of the electron wave function, using

either an analytical approach to solving the Aharonov–Bohm integral (7.35), or a nu-

merical approach based on the Mansuripur algorithm introduced in equation (7.42)

on page 456. An example of an analytical approach to the computation of the phase

shift for a uniformly magnetized spherical particle can be found in [DGNM99].

Pseudo code

PC-22 outlines a typical Lorentz image computation, as imple-

mented in the ION routine

lorentz.pro. The routine asks the user for several micro-

scope parameters (accelerating voltage, defocus, defocus spread, astigmatism, aper-

ture radius and position) and computes either a through-focus series (Fresnel mode)

or an aperture shift series (Foucault mode). The actual computation is carried out by

a Fortran program

LorentzExample.f90; this program computes the magnetization

conﬁguration, the resulting phase shift, and then applies the Lorentz contrast trans-

fer function T

to the reciprocal wave function. The resulting images are stored in

a TIFF ﬁle or sent back to the remote browser in the case of the ION version.

Next, we will discuss two example magnetization conﬁgurations: two parallel

180

◦

domain walls and the 2D conﬁguration of Fig. 7.35(a).

10.4.1 Example Lorentz image simulations for periodic

magnetization patterns

The simulations in this section were carried out using the ION implementation of

pseudo code

PC-22 . The reader may experiment with this program and vary all

parameters to study their inﬂuence on the image features.

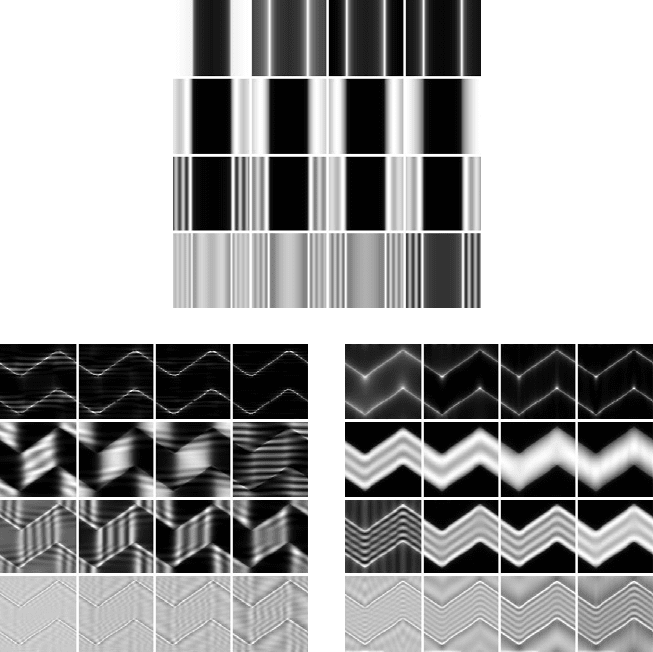
Figure 10.32 shows four Fresnel series for a pair of 180

◦

domain walls (a and b),

and for the intersecting 71

◦

and 180

◦

domain walls of Fig. 7.35(a). The microscope

parameters are listed in the ﬁgure caption; the image sequences (c) and (d) have

the same sequence of defocus values as the labeled values in Fig. 10.32(a). The

ﬁrst Fresnel series (a) shows that domain walls show up as bright or dark lines for

10.4 Lorentz image simulations 643

Pseudo Code PC-22 Outline of a Lorentz image simulation.

Input: 2D periodic magnetization conﬁguration

Output: exit wave phase and images

DFFT of magnetization components → M

compute phase φ for given beam direction, foil thickness {7.42}

DFFT of exit wave e

iφ

ask user for microscope data

if Fresnel mode then

for each defocus value do

compute contrast transfer function

multiply with reciprocal wave function

compute modulus squared of inverse DFFT

end for

end if

if Foucault mode then

for each aperture position do

compute contrast transfer function

multiply with reciprocal wave function

compute modulus squared of inverse DFFT

end for

end if

output to TIFF ﬁle

out-of-focus images. We will show below that the Fresnel image contrast occurs

wherever the phase proﬁle has non-zero curvature.

The through-focus series in Fig. 10.32(b) differs from that in (a) only in the value

of the beam divergence angle θ

; smaller values indicate a more coherent beam, and

the wall images consist of parallel fringes, as predicted in Section 7.5.2. Figure 10.33

shows how the fringe contrast at a 180

◦

domain wall changes with image defocus

for a beam divergence angle of θ

= 10

−5

and 10

−6

rad and a defocus range of ±0.5

mm. The fringe contrast is strong for the convergent wall image (right-hand side)

but nearly vanishes for the divergent wall image. The fringe spacing is determined

by the product B

t, as described in Section 7.5.2. A smaller beam divergence angle

extends the defocus range for which Fresnel fringes are visible.

The through-focus series in Fig. 10.32(c) shows that the contrast of 180

◦

domain

walls is signiﬁcantly stronger than that of 71

◦

walls, implying that the larger the

change in magnetization (either magnitude or direction) across the domain wall, the

more pronounced the image contrast. The through-focus series in Fig. 10.32(d) is

644 Phase contrast microscopy

-75 -65 -55 -45

-35 -25 -15 -5

5152535

45 55 65 75

(a) (b)

Fig. 10.32. Fresnel image simulations for two parallel 180

◦

domain walls (a) and (b), and for

the domain conﬁguration in Fig. 7.35(a), (c) and (d). The microscope accelerating voltage

is 200 kV, B

t = 100 nm T, θ

= 0.1 mrad, aperture radius q

= 0.2nm

−1

. (a) and (c) show

calculated images for a defocus range from −75 to +75 µm, (b) has θ

= 0.001 mrad and a

defocus range of ±750 µm, and (d) is similar to (c), except that astigmatism is included in

the computation (C

= 8 µm, φ

= 60

◦

). The intensity of each individual image was scaled

between 0 and 255.

identical to that in (c), except for the presence of two-fold astigmatism (C

= 8 µm,

= 60

◦

). Comparing the image for a defocus of +5 µm to the corresponding

image without astigmatism shows that astigmatism can completely remove the

contrast for domain walls in certain orientations, while enhancing the contrast for

other orientations. It is hence imperative that astigmatism be corrected properly, so

that for the in-focus condition no domain wall contrast is observed.

We will now show that Fresnel contrast occurs wherever the phase proﬁle has a

non-zero curvature. Consider a magnetic thin foil which gives rise to a phase shift

φ(r), where r is a vector in the plane normal to the electron beam. The phase shift

10.4 Lorentz image simulations 645

t = 200 nm T

= 0.01 mrad

t = 100 nm T

= 0.001 mrad

-0.5 mm 0.5 mm

(a)

(b)

0.0 mm

Image defocus

100 nm

Fig. 10.33. Fresnel through-focus montage for a 180

◦

domain wall of width δ = 60 nm.

The beam divergence angle is θ

= 10

−4

rad for the upper image and θ

= 10

−6

rad for the

bottom one.

includes both magnetic and electrostatic contributions, as described in Chapter 7

(equation 7.35). The exit wave function can be written as

ψ(r) = a(r)e

iφ(r)

The sample thickness may be non-uniform. We start from the Lorentz transfer

function (10.73). For small deﬂection angles (i.e. small |q|), and small defocus

values  f , we can ignore the fourth-order terms in z

and we write for the paraxial

wave function in the back focal plane:

ψ(q) = F[ψ(r)]



1 − z



, (10.75)

where z

= z

+ iz

(see equation 10.73). We have conveniently ignored the aper-

ture function A(q); we will assume that the aperture has a small enough radius to

646 Phase contrast microscopy

exclude all Bragg reﬂections. This means that the exit wave ψ(r) is essentially the

bright ﬁeld wave, which may be split into multiple components by the magnetic

domain structure of the sample, as illustrated in Fig. 7.35(c). The wave function

in the image plane is given by the inverse Fourier transform of equation (10.75),

which is (dropping the argument r):

ψ = ae

iφ

− z

−1

iφ

. (10.76)

Writing F[ae

iφ

] = f (q)wehave

−1

iφ

f (q)e

2πiq·r

−1

4π

f (q)∇

2πiq·r

−1

4π

∇

−1

[

f (q)

]

−1

4π

∇

iφ

and therefore

ψ = ae

iφ

4π

∇

iφ

. (10.77)

The image intensity is then given by the modulus squared of this expression, and

we leave it to the reader to show that (ignoring terms in λ

and in the absence of

astigmatism):

I = a

−

λ f

2π

∇·



∇φ



(

 f

)

a∇

a − a

(∇φ)

. (10.78)

For a uniform background intensity we have a

= 1, and therefore

I = 1 −

λ f

2π

∇

φ −

(

 f

)

(∇φ)

. (10.79)

For realistic conditions, the last term will be small compared to the other two, and

we ﬁnd that the image intensity is unity everywhere except when ∇

φ is non-zero,

or, equivalently, wherever the curvature of the phase is non-zero. For a constant foil

thickness, magnetic contrast will be visible only in those regions where the gradient

of the phase ∇φ is not constant, i.e. at the domain walls. The image contrast is also

linear in the defocus  f , which explains the contrast reversal between under-focus

and over-focus images.

Foucault domain contrast can also be simulated using the

LorentzExample.f90

program by simply moving the aperture to an off-axis location. Figure 10.34 shows

three sets of simulated Foucault images for a pair of 180

◦

domain walls (a), and for

10.4 Lorentz image simulations 647

0.1825 0.1850 0.1875 0.1900

0.1925 0.1950 0.1975 0.2000

0.2025 0.2050 0.2075 0.2100

0.2125 0.2150 0.2175 0.2200

(a)

(b) (c)

Fig. 10.34. Simulated Foucault series for a 0.2nm

−1

radius aperture and the indicated

aperture shifts. Imaging parameters are identical to those used for Fig. 10.32. The aperture

shift is in the horizontal direction for (a) and (b), and along the vertical direction for (c).

the intersecting domains of Fig. 7.35 (b and c). The material parameters are identical

to those used in Fig. 10.32. The aperture radius is q

= 0.2nm

−1

; the aperture

shifts are indicated by the numbers in Fig. 10.34(a). Foucault contrast appears

when the aperture begins to intersect the beams deﬂected by the various magnetic

domains. The easiest way to visualize this is with respect to Fig. 7.35(c): imagine

an aperture that just encloses all four deﬂected beams. When this aperture is moved

in any direction, one or more of the beams will be cut off and the corresponding

magnetic domain will become dark. If the aperture shift directions are calibrated

with respect to the image orientation, then it is in principle possible to derive the

local magnetization direction from a pair of Foucault images with aperture shifts

in independent directions.