Graef M. Introduction to conventional transmission electron microscopy
Подождите немного. Документ загружается.

648 Phase contrast microscopy
10.4.2 Fresnel fringes for non-magnetic objects
In the previous section, we saw that Fresnel (fringe) contrast occurs wherever the
phase of the electron wave has a non-vanishing second derivative (curvature). This
is valid for any phase, not just for phase of a magnetic origin, so in this section
we will explore briefly the nature of Fresnel fringes for non-magnetic objects.
From the Aharonov–Bohm equation we see that a non-magnetic object will cause
a phase shift which is entirely due to the electrostatic lattice potential. At low
magnifications, significantly lower than those used for high-resolution observations,
the only important component of the electrostatic lattice potential is the mean inner
potential V
0
, so that the phase shift due to a foil of thickness t is given by φ
e
= σ V
0
t,
where σ is the interaction constant. From here on we will drop the subscript 0 on
the mean inner potential and simply write V .
The ION routine
fresnel.pro can be used to display Fresnel images for objects
with a spatially varying mean inner potential. The routine provides the following
pre-defined sample “shapes”: a strip of material, a foil with a circular hole, a disk-
shaped island, a square island, and a thin strip of material with a slightly lower mean
inner potential than the surrounding matrix. The routine calls a Fortran program
that is very similar to the
LorentzExample.f90 program discussed earlier. The only
difference is that the phase computation is much simpler than for a magnetic object:
if the geometry of the object is known, then the local thickness can be computed
for a given orientation, and hence the phase shift will be known.
Figure 10.35 shows four pairs of simulated images for a circular hole in a matrix.
The matrix is 20 nm thick and has a mean inner potential of 30 V; the normal
absorption length is taken to be 50 nm. The exit wave function is then equal to
φ(x, y) = e
−t/ξ
e
iσ Vt
for x
2
+ y
2
> r
2
,
with r the radius of the hole. The origin is taken at the center of the hole. The exit
wave is unity inside the hole. The image pair a–b of Fig. 10.35 shows Fresnel fringes
for the defocus values ±150
µm (same values for all images in this figure). The
beam divergence angle is θ
c
= 0.05 mrad, and several Fresnel fringes are visible
near the edge of the hole, which is indicated by a thin white circle in all simulated
images. The first fringe inside the hole is bright for positive defocus and dark for
negative defocus. In the presence of astigmatism (C
a
= 100 µm and C
a
= 60
◦
),
the distance between the first fringe and the edge of the hole is no longer constant
and varies around the hole, as shown in image pair c–d. Conversely, if the first
fringe is not at the same distance from the edge for all points along the hole, then
astigmatism must be present. Correcting the astigmatism is then simply reduced to
making the Fresnel fringe continuous around the hole at a uniform distance from
the edge.

10.5 Exit wave reconstruction 649
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
150 nm
∆f = + 150 µm
∆f = - 150 µm
θ
c
= 0.05 mrad
θ
c
= 0.005 mrad
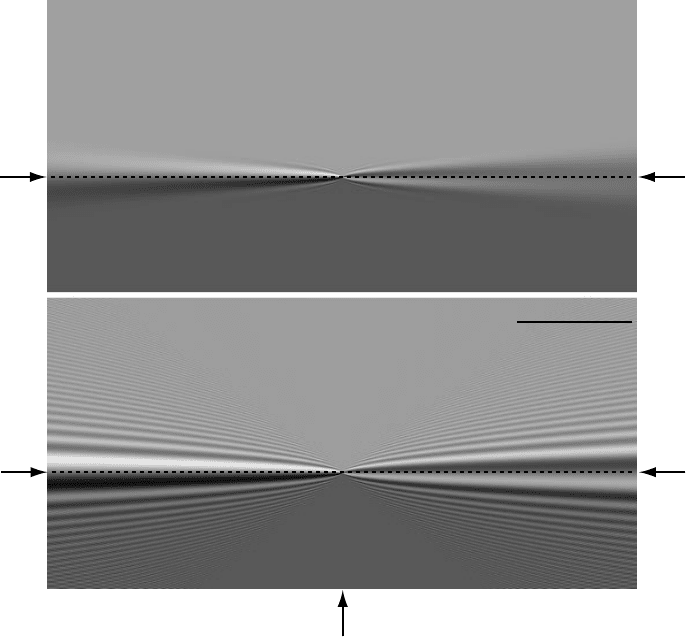
Fig. 10.35. Fresnel fringe simulations for a 300 nm diameter circular hole in a 20 nm thick
matrix with a mean inner potential of 30 V. The defocus is +150 µm for the top row, and
−150 µm for the bottom row. The four images on the left have θ
c
= 0.05 mrad, while the
others have θ
c
= 0.005 mrad. Image pairs c–d and g–h contain astigmatism (C
a
= 100 µm
and C
a
= 60
◦
). The images were computed using the ION routine fresnel, available from
the
website.
If the beam divergence angle is decreased to θ
c
= 0.005 mrad (this is possible for
a field emission microscope), then a much larger number of Fresnel fringes can be
observed, as illustrated by image pair e–f in Fig. 10.35. The presence of astigmatism
(g–h) can be recognized easily from the asymmetry of the fringes. The number of
fringes and the defocus range for which they are visible are illustrated in Fig. 10.36.
The top image represents a through-focus series ( f from −150 to +150
µm) for
a solid–vacuum interface; the foil thickness is 20 nm, with a mean inner potential
of 30 V. The interface is indicated by a dashed line. The beam divergence angle
is θ
c
= 0.1 mrad, which represents a low beam coherence. The Fresnel fringes are
visible for small defocus magnitudes but disappear for larger values. For a beam
divergence of 0.001 mrad, many fringes are visible (bottom of Fig. 10.36) even
for large defocus values. The fringes inside the foil may not always be visible,
depending on the thickness and absorption length of the foil.
10.5 Exit wave reconstruction
10.5.1 What are we looking for?
In virtually every TEM experiment we are ultimately interested in the structure
and/or chemistry of a particular material or defect. This means that we would
650 Phase contrast microscopy
-150 µm
150 µm
∆f = 0 µm
vacuum
solid
100 nm
θ
c
= 0.1 mrad
θ
c
= 0.001 mrad
Fig. 10.36. Through-focus series of Fresnel fringes near a straight edge. The microscope
accelerating voltage is 200 kV, foil thickness 20 nm, mean inner potential 30 V, and two
different beam divergence angles are shown.
like to find out where the individual atoms are located, or how the magnetization is
distributed throughout the thin foil, or where charges accumulate near an electrically
active boundary, and so on. For non-periodic features, such as most defects, we
may have a structure model that we can use to simulate images which can then be
compared with the observations. This is the standard approach which we will call
the forward approach:
atom positions → lattice potential → exit wave function → simulated images.
(10.80)
From the differences between observed and simulated images we can often derive
information to refine the model, and we may be able to iterate the model parameters
until the simulated images converge to the observed ones.
10.5 Exit wave reconstruction 651
In the forward approach, we typically do not modify the observed intensities,
other than perhaps some noise filtering and intensity and/or magnification scaling.
We use the observed images (they could also be diffraction patterns) as the reference
state against which to validate the model. We could also think about an opposite
approach, in which we attempt to derive the structure directly from the observed
images, with as few adjustable parameters as possible. This is known as the inverse
approach or, more commonly, as the inverse problem. While it may seem obvious
that this would be a possible approach, the inverse problem is actually a highly
non-trivial problem, since it requires that we reconstruct both the amplitude and
the phase of the electron wave at the exit plane of the sample. Phase information
is present in the images, but generally not in a form that can be extracted easily.
Ultimately, we want to find out what the electrostatic lattice potential looks like,
since it contains information on both the atom types and locations. This means
that we must invert the Schr¨odinger equation, in addition to removing the transfer
function of the microscope. The inverse problem can then be stated schematically
as follows:
experimental images → exit wave function → lattice potential → atom positions.
(10.81)
The first step, from image to wave function, is known as exit wave restoration
or reconstruction. It is a highly non-linear problem, since it essentially involves
the deconvolution of the microscope transfer function according to equation (2.56)
on page 107. We know from the first section of this chapter that the microscope
transfer function has multiple zero-crossings, so that a simple deconvolution is
not possible. The second step requires inversion of the Schr¨odinger equation,
and this is again a non-trivial step. Both problems have received considerable at-
tention, even since the early days of TEM research. There are several solutions
available in the literature, but none of them is entirely satisfactory in the sense
that no single method can be applied to all possible situations. Exit wave recon-
struction remains a topic of significant interest, in particular now that spherical
aberration can be removed from the image formation process using an aberration
corrector.
There is a significant body of literature on wave function restoration. The main
ideas go back to the work by Gerchberg and Saxton [GS72], Schiske [Sch68],
and ultimately to Cowley and Moodie [CM57]. The phase of the image wave
can be found from combinations of multiple images acquired at different micro-
scope defocus values, sometimes combined with diffraction information. Schiske’s
original work introduces so-called filter functions, which are essentially weight-
ing functions used to combine images taken at multiple defocus values in such
a way that a least-squares best estimate of the exit wave function is obtained.
652 Phase contrast microscopy
This procedure is now known as a generalized Wiener filter, as described in
[HK94, Chapter 73].
Kirkland and coworkers [KSUF80, Kir82, KSUF82] have successfully imple-
mented a reconstruction scheme based on a minimum mean-square formalism
and applied it to what has effectively become a “standard sample”, chlorinated
Cu-phthalocyanine. Adaptive least-squares filters were introduced by Hawkes
[Haw74], and a review of various filter methods can be found in [Sch84]. The
Gerchberg–Saxton algorithm makes use of an image and a diffraction pattern taken
from the same region [GS72, GS73]; a multiple image algorithm, proposed by
Misell [Mis73], and elaborated by many others, can in principle be used to recover
the phase from two images at different microscope defocus, but no experimental
verification of the method has been reported. Kirkland’s multiple input maximum a
posteriori method (MIMAP) [Kir84, KSUF85] again works in principle, but does
not function satisfactorily for realistic experimental conditions. Non-linear recon-
struction schemes based on the earlier work have also been proposed [CJOdBVD92]
and have been shown to work in selected experimental situations. For an in-depth
review of other reconstruction schemes we refer to Chapters 73 and 74 in [HK94].
A review of exit wave reconstruction using electron holography methods can be
found in [VAJ99].
In the next section, we will illustrate the process of exit wave reconstruction
for Lorentz imaging. The reconstruction process for Lorentz images is much more
straightforward than for conventional high-resolution images, since we can make
good use of the fact that the Lorentz deflection angle is small compared with the
Bragg angle. As we will see in the next section, this makes it possible to derive the
phase of the exit wave from just three experimental images.
10.5.2 Exit wave reconstruction for Lorentz microscopy
We start from equation (10.78) and write the in-focus intensity a
2
as I (r, 0); the out-
of-focus image intensity is then written as I (r,f ). Next, we derive an equation for
the phase φ; consider an under-focus and over-focus image, for the same defocus
magnitude | f |:
I (r, | f |) = I (r, 0) −
λ| f |
2π
∇·
(
I (r, 0)∇φ
)
+
(
θ
c
| f |
)
2
2ln2
<
I (r, 0)∇
2
I (r, 0) − I (r, 0)(∇φ)
2
=
;
I (r, −| f |) = I (r, 0) +
λ| f |
2π
∇·
(
I (r, 0)∇φ
)
+
(
θ
c
| f |
)
2
2ln2
<
I (r, 0)∇
2
I (r, 0) − I (r, 0)(∇φ)
2
=
.

10.5 Exit wave reconstruction 653
Subtracting the second equation from the first, and rearranging terms we have:
−
2π
λ
I (r, | f |) − I (r, −| f |)
2| f |
=∇·
[
I (r, 0)∇φ
]
. (10.82)
In the limit of vanishingly small defocus the left-hand side becomes a derivative and
we arrive at the so-called transport-of-intensity equation (TIE)
†
[Tea83, GRN95b,
GRN95a, GN96, PN98]:
∇·
[
I (r, 0)∇φ
]
=−
2π
λ
∂ I (r, 0)
∂z
.
(10.83)
The TIE equation was also derived by Van Dyck and Coene in 1987 starting from
equation (5.35) with
¯
V = 0 (i.e. the free-space propagation equation) [VDW87].
Note that the beam divergence term, which is even in the defocus, cancels out in
the difference between under-focus and over-focus images. This means that phase
reconstruction for Lorentz microscopy images does not require a highly coherent
electron beam.
10.5.2.1 Solving the TIE equation
Equation (10.83) can be solved numerically in a number of different ways. Perhaps
the most straightforward method relies on the use of fast Fourier transforms. The
Fortran source code for the algorithm can be found on the
website in the routine
TIE.f90. A formal solution to the TIE equation can be derived by introducing a new
variable , such that
∇(r, 0) ≡ I (r, 0)∇φ. (10.84)
If the phase is entirely determined by the magnetic structure of the thin foil,
then its gradient can be used to compute the in-plane magnetic induction
configuration:
∇φ =
∇
I (r, 0)
=−
e
h
[
B(r) × n
]
t(r), (10.85)
where n is the unit normal in the beam direction and t is the local sample thickness.
Using the function defined in equation (10.84), the TIE becomes a Poisson-
type equation [PN98]:
∇
2
(r, 0) =−k
∂ I (r, 0)
∂z
. (10.86)
†
The name of this equation was first coined by M.R.Teague [Tea83], who showed that this formalism could be
applied to phase retrieval.

654 Phase contrast microscopy
While a direct analytical solution is difficult to obtain, it is possible to write down
a symbolic solution as follows:
(r, 0) =−k∇
−2
∂ I (r, z)
∂z
. (10.87)
The symbol ∇
−2
refers to the two-dimensional inverse Laplacian operator, and
we will describe shortly a simple numerical implementation. Taking the two-
dimensional gradient of this equation we obtain:
∇φ(r, 0) =−
k
I (r, 0)
∇∇
−2
∂ I (r, 0)
∂z
, (10.88)
where we have used equation (10.84). After applying the two-dimensional diver-
gence operator ∇·, and bringing the Laplacian operator to the right-hand side we
find the symbolic solution for the phase [PN98]:
φ(r, 0) =−k∇
−2
∇·
1
I (r, 0)
∇
6
∇
−2
∂ I (r, 0)
∂z
>
. (10.89)
It is straightforward to show that the same equation can be used to recover the phase
for an out-of-focus image; the argument (r, 0) can then be replaced by (r,f ).
While equation (10.89) looks rather menacing, it is actually not very difficult
to implement an efficient numerical procedure to solve for the phase. In fact,
we can take the formal solution one step further and note that (at least formally)
we have
∇
−2
∇=∇
−1
=∇∇
−2
, (10.90)
and we arrive at the formal solution
φ(r, 0) =−k∇
−1
·
1
I (r, 0)
6
∇
−1
∂ I (r, 0)
∂z
>
.
(10.91)
From equation (10.82) we see that we need to acquire two out-of-focus images,
I (r, − f ) and I (r, + f ). In addition, according to equation (10.89), we need
the in-focus image I (r, 0). The longitudinal derivative ∂ I /∂z can be computed
readily, provided both images are perfectly aligned and have precisely the same
magnification.
†
From equations (10.76) and (10.77) we can derive the following
relation:
∇
2
[···] =−4π
2
F
−1
$
F[···]|q|
2
%
, (10.92)
†
Recall that the magnification changes with defocus, in particular when a low-field lens with a long focal length
is used.

10.5 Exit wave reconstruction 655
where [···] indicates a function of the coordinate variable r. We leave it to the
reader to show that
∇
−2
[···] =−
1
4π
2
F
−1
F[···]
|q|
2
. (10.93)
If we combine the inverse Laplacian with the gradient operator ∇, then we can
show that with respect to the Cartesian reference frame e
i
we have for every
function α(r)
∇
−1
α(r) =∇∇
−2
α(r) =∇
−2
∇α(r);
=−
1
4π
2
∂
∂x
j
F
−1
q
F
r
[α(r)]
|q|
2
e
j
;
=−
i
2π
..
α(r
)
..
q
|q|
2
e
2πiq·(r−r
)
dq
dr
;
=
i
2π
..
α(r − R
⊥
)
..
q
|q|
2
e
2πiq·R
⊥
dq
dR
⊥
;
≡
i
2π
..
α(r − R
⊥
)G(R
⊥
)dR
⊥
;
=
i
2π
G(r) ⊗ α(r).
The vector function G(r) is equal to the inverse Fourier transform of the vector
function q/|q|
2
, and is not defined for q = 0. The formal solution (10.91) to the
TIE equation can then be expressed as a double convolution product:
φ(r,f
j
) =
δ
2
64π
3
λ f
(G(r)⊗) ·
G(r) ⊗ ∂ I (r,f
j
)/∂z
I (r,f
j
)
. (10.94)
It is understood that the integrations are carried out on a grid with unit grid spacing.
In component notation we have
G(r) ⊗ [···] = e
i
γ
i
⊗ [···] = e
i
..
q
i
|q|
2
e
2πiq·r
dq
⊗ [···],
and for numerical implementation we can use
φ =−
δ
2
64π
3
λ f
2
i=1
γ
i
⊗
γ
i
⊗ ∂ I /∂z
I
, (10.95)
where γ
i
are the components of the vector function G. The prefactor follows from
a simple dimensional analysis of the formal solution (10.91). This particular form
of the symbolic solution shows clearly that the accuracy of the magnitude of the
reconstructed phase depends directly on a careful calibration of the microscope

656 Phase contrast microscopy
Pseudo Code PC-23 Reconstruct exit wave phase from Lorentz–Fresnel images.
Input: Three or five images, δ, f , λ {Microscope calibration!}
Output: Reconstructed exit wave phase
compute array of
q
|q|
2
vectors
compute longitudinal derivative
ˆ
∇
z
I
verify conservation criterion
convolve with G(r) (using FFT operations)
divide by the in-focus image
convolve with G(r) (using FFT operations)
normalize with the prefactor
δ
2
64π
3
λ f
magnification (through δ) and the defocus step size ( f ). Pseudo code for the
implementation of equation (10.95) can be found in
PC-23 . Since part of the
reconstruction involves a convolution product, one must take care of aliasing effects
and truncate the Fourier transforms at
2
3
q
c
. Since the inverse Laplacian is effectively
a low-pass filter, this does not cause any loss of information.
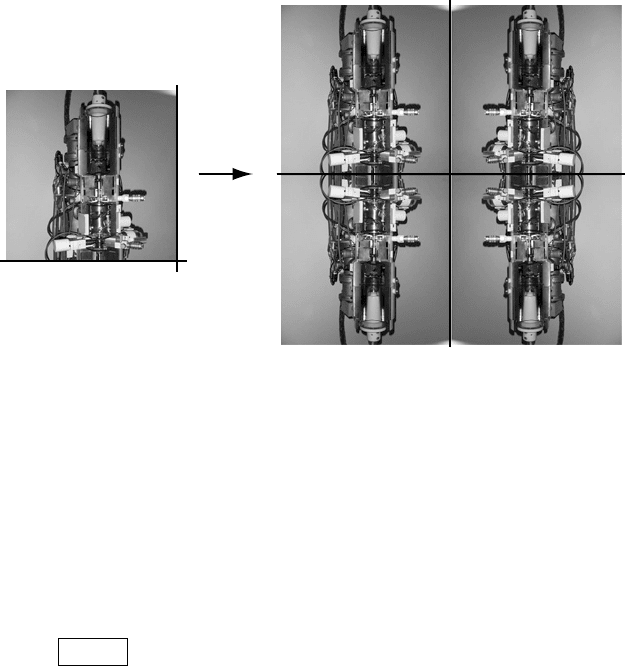
In addition to the anti-aliasing measures, we must also symmetrize the in-
put images, to ensure that the solution to the TIE equation is unique. The rea-
sons for this symmetrization are beyond the scope of this textbook and we re-
fer the interested reader to [VZDG02] for the details. In practice, we double the
size of the images by application of two orthogonal mirror planes, as shown in
Fig. 10.37. The algorithm is then applied to the symmetrized images. The main
reason for this symmetrization is the use of the fast Fourier transform, which re-
quires a periodic input image. An example computation is shown in the following
section.
Finally, the right-hand side derivative in the TIE must average to zero, indicating
that no electrons are lost from the image with varying defocus. This conservation
criterion guarantees that the solution to the TIE is unique [GRN95a].
While we have used the small-angle approximation to the transfer function, it
can be shown (e.g. [BPN00, Chapter 5] and [VDW87]) that the TIE equation is
valid for a much more general class of experimental configurations. It is possible
to apply the same formalism to high-resolution phase contrast images, and one can
then reconstruct the phase of the image wave from a through focus series consisting
of at least three images. When the phase of the image wave is known, a Fourier
transform propagates the wave back to the back focal plane of the objective lens,
where one can then deconvolve the transfer function. This phase reconstruction
method is rather promising when used in combination with a spherical aberration
10.5 Exit wave reconstruction 657
m
m
(a)
(b)
Fig. 10.37. Symmetrization of the images needed to solve the transport-of-intensity equa-
tion using a fast Fourier transform algorithm.
corrector, since the zero-crossings of the transfer function can then be avoided
entirely.
10.5.2.2 Example application of the TIE formalism
The TIE solution algorithm has been applied to the Fresnel images of Fig. 4.28.
The area indicated by a square was taken as the input image (160 × 160 pixels).
After aligning the three images using a cross-correlation algorithm, the algorithm in
pseudo code
PC-23 was applied. The resulting reconstructed phase is shown as a
grayscale image in Fig. 10.38(a) and a contour plot in (b). The x and y components
of the gradient of φ are proportional to the y and x components of the integrated
magnetic induction and are shown in Figs 10.38(c) and (d); bright areas indicate
positive components. A more familiar representation of the magnetic induction in
the foil is shown in Fig. 10.39: each vector represents the average induction over
a4× 4 pixel area. Vector lengths are scaled with respect to the longest vector
which has unit magnitude. The vortex and cross-tie wall are clearly visible in the
reconstructed map.
As a final example we consider a 2 × 1
µm rectangular Permalloy island de-
posited on a Si
3
N
4
membrane, observed in Fresnel mode on a JEOL 4000EX
microscope equipped with a Gatan post-column energy filter (GIF). The under-
and over-focus images are shown in Figs 10.40(a) and (b), along with the numer-
ically computed derivative ∂ I /∂ z, shown in (c). The image consists of 300 × 300
pixels. The reconstructed phase is shown as a grayscale plot (d) and as cos φ (e).
The square region outlined in (c) is shown in (f) as a vector plot, obtained from the
x and y components of ∇
⊥
φ.
