Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 161

calculating probabilities

Handy hints for working with trees

1. Work out the levels

Try and work out the different levels of probability that you need.

As an example, if you’re given a probability for P(A | B), you’ll

probably need the first level to cover B, and the second level A.

2. Fill in what you know

If you’re given a series of probabilities, put them onto the tree in

the relevant position.

3. Remember that each set of branches sums to 1

If you add together the probabilities for all of the branches

that fork off from a common point, the sum should equal 1.

Remember that P(A) = 1 - P(A

4. Remember your formula

You should be able to find most other probabilities by using

P(A | B) = P(A

∩

P(B)

162 Chapter 4

Donuts

Coffee

Donuts

Coffee

3/4

1/4

2/5

3/5

1/3

2/3

These must

add up to 1.

These must add

up to 1 as well.

P(Coffee | Donuts) = P(Coffee

∩

Donuts)

P(Donuts)

= 9/20

3/4

= 3/5

These need to

add up to 1.

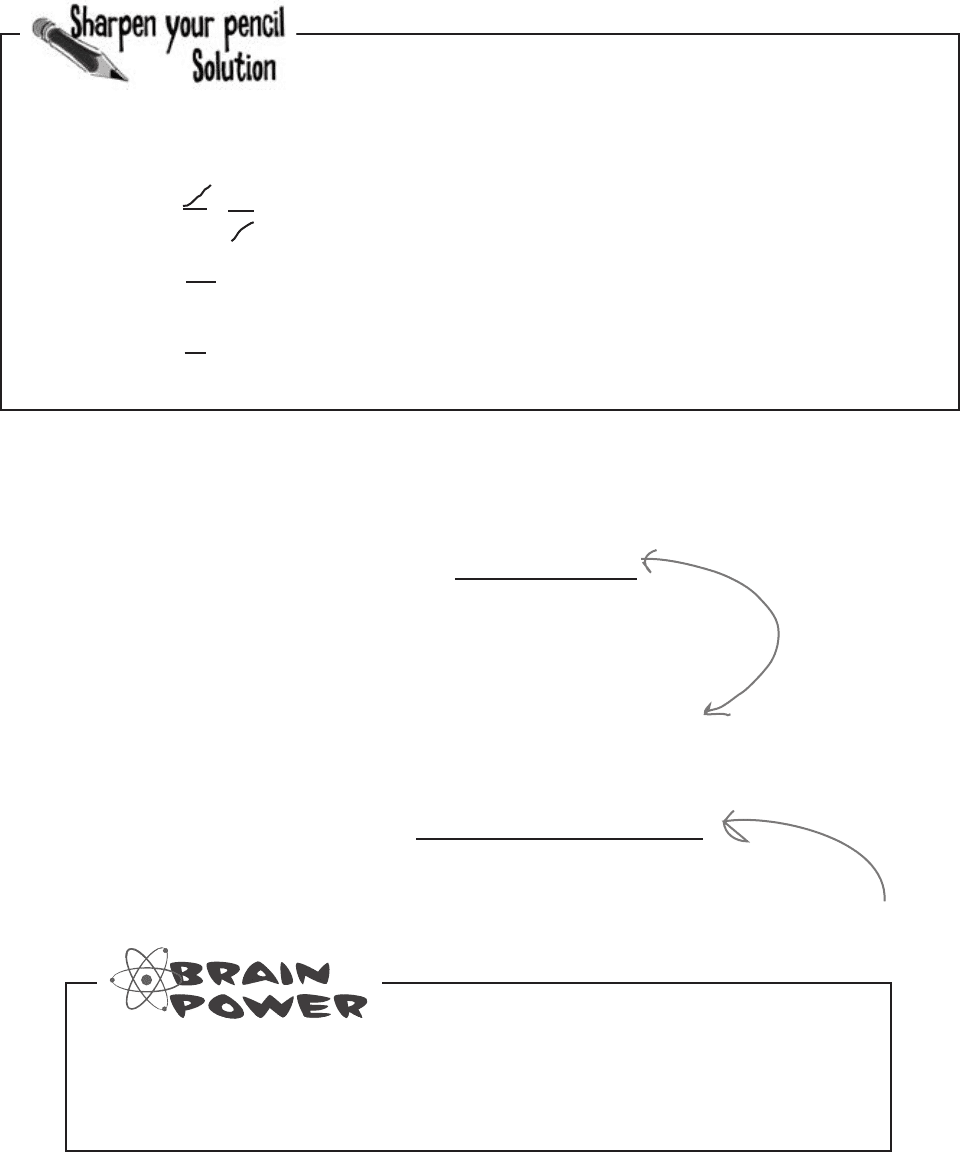
Probability Magnets Solution

Duncan’s Donuts are looking into the probabilities of their customers

buying Donuts and Coffee. They drew up a probability tree to show the

probabilities, but in a sudden gust of wind they all fell off. Your task is to pin

the probabilities back on the tree. Here are some clues to help you.

P(Donuts) = 3/4 P(Coffee | Donuts

) = 1/3 P(Donuts ∩ Coffee) = 9/20

probability magnets solution

you are here 4 163

calculating probabilities

1. P(Donuts

)

3. P(Coffee

| Donuts)

5. P(Donuts | Coffee)

2. P(Donuts

∩ Coffee)

4. P(Coffee)

We haven’t quite finished with Duncan’s Donuts! Now that you’ve completed

the probability tree, you need to use it to work out some probabilities.

Hint: maybe some of your

other answers can help you.

Hint: How many ways are

there of getting coffee?

(You can get coffee with or

without donuts.)

164 Chapter 4

1. P(Donuts

)

3. P(Coffee

| Donuts)

5. P(Donuts | Coffee)

2. P(Donuts

∩ Coffee)

4. P(Coffee)

1/4 1/12

2/5

8/15

27/32

Your job was to use the completed probability tree to work out some probabilities.

We can read this one off the tree.

We were given

P(Donuts) = 3/4,

so P(Donuts

) must be 1/4.

We can read this

off the tree.

You’ll only be able to do this if you found P(Coffee).

P(Donuts | Coffee) = P(Donuts

∩

Coffee) / P(Coffee).

This gives us (9/20) / (8 / 15) = 27/32.

We can find this by multiplying together

P(Donuts

) and P(Coffee

Donuts

). We’ve

just found P(Donuts

) = 1/4, and looking

at the tree, P(Coffee

Donuts

) = 1/3.

Multiplying these together gives 1/12.

This probability is tricky, so don’t worry if you

didn’t get it.

To get P(Coffee), we need to add together

P(Coffee

∩ Donuts) and P(Coffee

∩ Donuts

This gives us 1/12 + 9/20 = 8/15.

exercise solution

you are here 4 165

calculating probabilities

Conditions

P(A | B) = P(A ∩ B)

P(B)

Vital StatisticsVital Statistics

I still don’t get the difference

between P(A

∩ B) and P(A | B).

A: P(A ∩ B) is the probability of getting

both A and B. With this probability, you can

make no assumptions about whether one

of the events has already occurred. You

have to find the probability of both events

happening without making any assumptions.

P(A | B) is the probability of event A given

event B. In other words, you make the

assumption that event B has occurred, and

you work out the probability of getting A

under this assumption.

So does that mean that P(A | B) is

just the same as P(A)?

A: No, they refer to different probabilities.

When you calculate P(A | B), you have to

assume that event B has already happened.

When you work out P(A), you can make no

such assumption.

Is P(A | B) the same as P(B | A)?

They look similar.

A: It’s quite a common mistake, but they

are very different probabilities. P(A | B)

is the probability of getting event A given

event B has already happened. P(B | A)

is the probability of getting event B given

event A occurred. You’re actually finding

the probability of a different event under a

different set of assumptions.

Are probability trees better than

Venn diagrams?

A: Both diagrams give you a way of

visualizing probabilities, and both have their

uses. Venn diagrams are useful for showing

basic probabilities and relationships, while

probability trees are useful if you’re working

with conditional probabilities. It all depends

what type of problem you need to solve.

Is there a limit to how many sets of

branches you can have on a probability

tree?

A: In theory there’s no limit. In practice

you may find that a very large probability

tree can become unwieldy, but you may still

find it easier to draw a large probability tree

than work through complex probabilities

without it.

If A and B are mutually exclusive,

what is P(A | B)?

A: If A and B are mutually exclusive, then

P(A

∩ B) = 0 and P(A | B) = 0. This makes

sense because if A and B are mutually

exclusive, it’s impossible for both events

to occur. If we assume that event B has

occurred, then it’s impossible for event A to

happen, so P(A | B) = 0.

166 Chapter 4

Bad luck!

You placed a bet that the ball would land in an even pocket

given we’ve been told it’s black. Unfortunately, the ball landed

in pocket 17, so you lose a few more chips.

Maybe we can win some chips back with another bet. This

time, the croupier says that the ball has landed in an even

pocket. What’s the probability that the pocket is also black?

We can reuse the probability calculations we

already did.

Our previous task was to figure out P(Even | Black), and we

can use the probabilities we found solving that problem to

calculate P(Black | Even). Here’s the probability tree we used

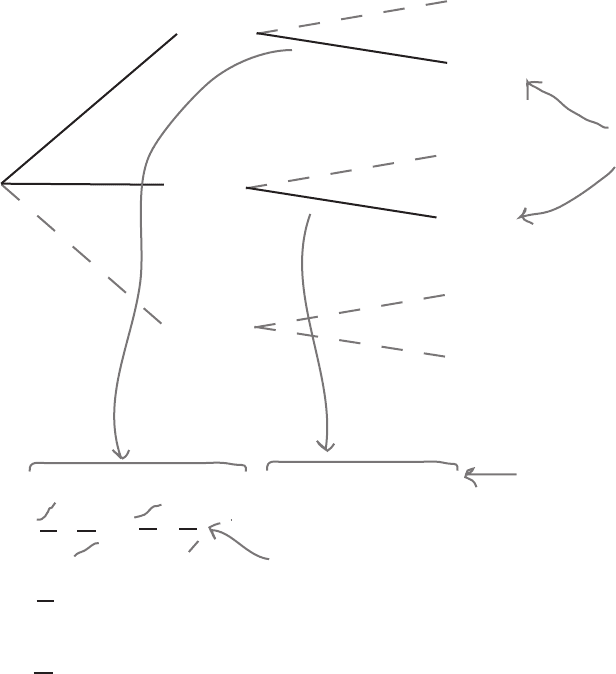
before:

This is the opposite

of the previous bet.

Black

Red

Green

Even

Odd

Even

Odd

18/38

2/38

8/18

10/18

1/2

But that’s a similar problem to the

one we had before. Do you mean we have

to draw another probability tree and work

out a whole new set of probabilities? Can’t

we use the one we had before?

a new conditional probability

you are here 4 167

calculating probabilities

So how do we find P(Black | Even)? There’s still a way of calculating

this using the probabilities we already have even if it’s not immediately

obvious from the probability tree. All we have to do is look at the

probabilities we already have, and use these to somehow calculate the

probabilities we don’t yet know.

Let’s start off by looking at the overall probability we need to find,

P(Black | Even).

Using the formula for finding conditional probabilities, we have

P(Black | Even) = P(Black ∩ Even)

P(Even)

If we can find what the probabilities of P(Black ∩ Even) and P(Even) are,

we’ll be able to use these in the formula to calculate P(Black | Even). All

we need is some mechanism for finding these probabilities.

Sound difficult? Don’t worry, we’ll guide you through how to do it.

Use the

probabilities

you have to

calculate the

probabilities

you need

Step 1: Finding P(Black ∩ Even)

Let’s start off with the first part of the formula, P(Black ∩ Even).

Take a look at the probability tree on the previous page. How can

you use it to find P(Black

∩ Even)?

Hint: P(Black

∩

Even) = P(Even

∩

Black)

We can find P(Black l Even) using the probabilities we already have

168 Chapter 4

Take a look at the probability tree opposite. How can you use it to

find P(Black

∩ Even)?

You can find P(Black ∩ Even) by multiplying together P(Black) and P(Even | Black). This gives us

P(Black

∩ Even) = P(Black) x P(Even | Black)

= 18 x 10

38 18

= 10

= 5

Take another look at the probability tree on page 168. How do you think we

can use it to find P(Even)?

P(Black | Even) = P(Black ∩ Even)

P(Even)

So where does this get us?

We want to find the probability P(Black | Even). We can do

this by evaluating

So far we’ve only looked at the first part of the formula,

P(Black ∩ Even), and you’ve seen that you can calculate

this using

So how do we find the next part of the formula, P(Even)?

P(Black ∩ Even) = P(Black)

P(Even | Black)

This gives us

P(Black | Even) = P(Black)

P(Even | Black)

P(Even)

These two quantities are

equivalent…

…so we can substitute P(Black) x P(Even | Black)

for P(Black

∩

Even) in our original formula.

sharpen solution

you are here 4 169

calculating probabilities

This gives us

P(Even) = P(Black ∩ Even) + P(Red ∩ Even)

= P(Black)

P(Even | Black) + P(Red)

P(Even | Red)

= 18

10 + 18

38 18 38 18

= 18

= 9

Step 2: Finding P(Even)

The next step is to find the probability of the ball landing in an even

pocket, P(Even). We can find this by considering all the ways in which

this could happen.

A ball can land in an even pocket by landing in either a pocket that’s

both black and even, or in a pocket that’s both red and even. These are

all the possible ways in which a ball can land in an even pocket.

This means that we find P(Even) by adding together P(Black ∩ Even)

and P(Red ∩ Even). In other words, we add the probability of the

pocket being both black and even to the probability of it being both red

and even. The relevant branches are highlighted on the probability tree.

These probabilities

come from the

probability tree.

Black

Red

Green

Even

Odd

Even

Odd

18/38

2/38

8/18

10/18

1/2

To find the probability

of the ball landing in an

even pocket, add these

probabilities together.

All the ways of the ball landing

in an even pocket

170 Chapter 4

Step 3: Finding P(Black l Even)

Can you remember our original problem? We wanted to find

P(Black | Even) where

P(Black | Even) = P(Black ∩ Even)

P(Ev

en)

= P(Black)

P(Even | Black)

P(Black)

P(Even | Black) + P(Red)

P(Even | Red)

= 5 ÷ 9

19 19

= 5

19 9

= 5

This means that we now have a way of finding new conditional

probabilities using probabilities we already know—something that can

help with more complicated probability problems.

Let’s look at how this works in general.

P(Black | Even) = P(Black ∩ Even)

P(Even)

P(Black ∩ Even) = P(Black)

P(Even | Black)

We started off by finding an expression for P(Black ∩ Even)

After that we moved on to finding an expression for P(Even), and

found that

P(Even) = P(Black)

P(Even | Black) + P(Red)

P(Even | Red)

Putting these together means that we can calculate P(Black | Even)

using probabilities from the probability tree

This is what we just calculated

using the probability tree.

We calculated these

earlier, so we can

substitute in our results.

generalizing reverse conditional probabilities