Griffiths D. Head First Statistics
Подождите немного. Документ загружается.

you are here 4 261
permutations and combinations
Examining combinations
Earlier on we found a general way of calculating permutations. Well,
there’s a way of doing this for combinations too.
In general, the number of combinations is the number of ways of
choosing r objects from n, without needing to know the exact order of the
objects. The number of combinations is written
n
C
r
, where
n
C
r
= n!
r! (n - r)!
This is the total
number of objects.
This is the number of
positions we want to fill.
You divide by an extra r! if it’s a combination.
This bit is calculated in the same way
as a permutation.
So what’s the difference between a combination and a permutation?
These are
the same
combination.
Combination: order doesn’t matter.
=
≠
Permutation: order matters.
Combinations
A combination is the number of ways in which you
can choose objects from a pool, without caring about
the exact order in which you choose them. It’s a lot
more general than a permutation as you don’t need to
know how each position has been filled. It’s enough to
know which objects have been chosen.
Permutations
A permutation is the number of ways in which you
can choose objects from a pool, and where the order in
which you choose them counts. It’s a lot more specific
than a combination as you want to count the number
of ways in which you fill each position.
These are
separate
permutations.
262 Chapter 6
Head First: Combination, great to have you on the
show.
Combination: Thanks for inviting me, Head First.
Head First: Now, let’s get straight onto business. A
lot of people have noticed that you and Permutation
are very similar to each other. Is that something
you’d agree with?
Combination: I can see why people might think
that because we deal with very similar situations.
We’re both very much concerned with choosing a
certain number of objects from a pool. Having said
that, I’d say that’s where the similarity ends.
Head First: So what makes you different?
Combination: Well, for starters we both have very
different attitudes. Permutation is very concerned
about order, and really cares about the exact order in
which objects are picked. Not only does he want to
select objects, he wants to arrange them too. I mean,
come on!
Head First: I take it you don’t?
Combination: No way! I’m sure permutation
shows a lot of dedication and all that, but quite
frankly, life’s too short. As far as I’m concerned, if an
object’s picked from the pool, then that’s all anyone
needs to know.
Head First: So are you better than permutation?
Combination: I wouldn’t like to say that either one
of us is better as such; it just depends which of us is
the most appropriate for the situation. Take music
players, for instance.
Head First: Music players?
Combination: Yes. Lots of music players have
playlists where you can choose which songs you want
to play.
Head First: I think I see where you’re headed...
Combination: Now, both Permutation and I
are both interested in what’s on the playlist, but in
different ways. I’m happy just knowing what songs
are on it, but Permutation takes it way further.
He doesn’t just want to know what songs are on
the playlist, he wants to know the exact order too.
Change the order of the songs, and it’s the same
Combination, but a different Permutation.
Head First: Tell me a bit about your calculation.
Is calculating a Combination similar to how you’d
calculate a Permutation?
Combination: It’s similar, but there’s a slight
difference. With Permutation, you find n!, and then
divide it by (n-r)!. My calculation is similar, except
that you divide by an extra r!. This makes me
generally smaller—which makes sense because I’m
not as fussy as Permutation.
Head First: Generally smaller?
Combination: I’ll phrase that differently.
Permutation is never smaller than me.
Head First: Combination, thank you for your time.
Combination: It’s been a pleasure.
Combination Exposed
This week’s interview:
Does order really matter?
Combination Exposed
This week’s interview:
Does order really matter?
interview with a combination

you are here 4 263
permutations and combinations
Q:
I’ve heard of something called
“choose.” What’s that?
A: It’s another term for the combination.
n
C
r
. basically means “you have n objects,
choose r,” so it’s sometimes called the
choose function.
Q:
Can a permutation ever be smaller
than a combination?
A: Never. To calculate a combination, you
divide by an extra number, so the end result
is smaller.
The closest you get to this is when a
permutation and combination are identical.
This is only ever the case when you’re
choosing 0 objects or 1.
Q:
Which is a permutation and which
is a combination? I get confused.
A: A permutation is when you care about
the number of possible arrangements of
the objects you’ve chosen. A combination
is when you don’t mind about their precise
order; it’s enough that you’ve chosen them.
Q:
I get confused. If I want to find the
number of combinations of choosing r
objects from n, do I write that
n
C
r
or
r
C
n
?
A: It’s
n
C
r
. One way of remembering this is
that the higher of the two numbers is higher
up in the shorthand.
Q:
Are there other ways of writing
this? I think I’ve seen combinations
somewhere else, but they didn’t look like
that.
A: There are different ways of writing
combinations. We’ve used the shorthand
n
C
r
,
but an alternative is
(
n
)
r
Q:
Are permutations and combinations
really important?
A: They are, particularly combinations.
You’ll see more of these a bit later on in the
book, so look out for when you might need
them.
Q:
Dealing with permutations and
combinations looks similar to when
you’re dealing with like objects. Is that
right?
A: It’s a similar process. When you’re
dealing with like objects, you divide the total
number of arrangements by the number of
ways in which you can divide the like objects.
For permutations, it’s as though you’re
treating all the objects you don’t choose as
being alike, so you divide n! by (n-r)!. For
combinations, it’s as though the objects you
pick are alike, too. This means you divide
the number of permutations by r!.
Permutations
If you choose r objects from a pool of n,
the number of permutations is given by
n
P
r
= n!
(n-r)!
Combinations
If you choose r objects from a pool of n,
the number of combinations is given by
n
C
r
= n!
r!(n-r)!
Vital StatisticsVital Statistics

264 Chapter 6
The Statsville All Stars are due to play a basketball match. There are 12 players in the roster,
and 5 are allowed on the court at any one time.
1. How many different arrangements are there for choosing who’s on the court at the same time?
2. The coach classes 3 of the players as expert shooters. What’s the probability that all 3 of these players will be on
the court at the same time, if they’re chosen at random?
combinations exercise

you are here 4 265
permutations and combinations
It’s time for you to work out some poker probabilities. See how you get on.
A poker hand consists of 5 cards and there are 52 cards in a pack. How many different
arrangements are there?
A royal flush is a hand that consists of a 10, Jack, Queen, King and Ace, all of the same suit. What’s the probability of
getting this combination of cards? Use your answer above to help you.
Four of a kind is when you have four cards of the same denomination. Any extra card makes up the hand. What’s the
probability of getting this combination?
A flush is where all 5 cards belong to the same suit. What’s the probability of getting this?

266 Chapter 6
The Statsville All Stars are due to play a basketball match. There are 12 players in the roster,
and 5 are allowed on the court at any one time.
1. How many different arrangements are there for choosing who’s on the court at the same time?
2. The coach classes 3 of the players as expert shooters. What’s the probability that all 3 of these players will be on
the court at the same time, if they’re chosen at random?
There are 12 players in the roster, and we need to count the number of ways of choosing 5 of them. We
don’t need to consider the order in which we pick the players, so we can work this out using combinations.
12
C
5
= 12!
5!(12-5)!
= 12!
5!7!
= 792
Let’s start by finding the number of ways in which the three shooters can be on the court at the
same time.
If the three expert shooters are on the court at the same time, this means that there are 2 more
places left for the other players. We need to find the number of combinations of filling these 2 places
from the remaining 9 players.
9
C
2
= 9!
2!(9-2)!
= 9!
2!7!
= 36
This means that the probability of all 3 shooters being on the court at the same time is
36/792 = 1/22.
exercise solution

you are here 4 267
permutations and combinations
It’s time for you to work out some poker probabilities. See how you get on.
A poker hand consists of 5 cards and there are 52 cards in a pack. How many different
arrangements are there?
There are 52 cards in a pack, and we want to choose 5.
52
C
5
= 52! = 2,598,960
47!5!
A royal flush is a hand that consists of a 10, Jack, Queen, King and Ace, all of the same suit. What’s the probability of
getting this combination of cards? Use your answer above to help you.
There’s one way of getting this combination for each suit, and there are 4 suits. This means that the
number of ways of getting a royal flush is 4.
P(Royal Flush) = 4
2,598,960
= 1/649,740
= 0.0000015
Four of a kind is when you have four cards of the same denomination. Any extra card makes up the hand. What’s the
probability of getting this combination?
Let’s start with the 4 cards of the same denomination. There are 13 denominations in total, which means
there are 13 ways of combining these 4 cards. Once these 4 cards have been chosen, there are 48 cards
left. This means the number of ways of getting this hand is 13x48 = 624.
P(Four of a Kind) = 624
2,598,960
= 1/4165
= 0.00024
A flush is where all 5 cards belong to the same suit. What’s the probability of getting this?.
To find the number of possible combinations, find the number of ways of choosing a suit, and then choose 5
cards from the suit. There are 13 cards in each suit. This means the number of combinations is
4 x
13
C
5
= 4 x 13!
8!5!
= 4 x 1287 = 5148
P(Flush) = 5148
2,598,960
= 33/16660
= 0.00198

268 Chapter 6
It’s the end of the race
The race between the twenty horses is over, and the
overall winner is Ruby Toupee, followed by Cheeky
Sherbet and Frisky Funboy. If you decided to bet on
these three horses, you just won big!
In this chapter, you’ve learned how to cope with different
arrangements, and how to quickly count the number of
possible combinations and permutations without having to
work out each and every possibility.
The sort of knowledge you’ve gained gives you enormous
probability and statistical power. Keep reading, and we’ll
show you how to gain even greater mastery.
Winner of this year’s
Statsville Derby:
Ruby Toupee
2nd place:
Cheeky Sherbet
3rd place:
Frisky Funboy
hooray for toupee!

this is a new chapter 269
geometric, binomial, and poisson distributions
7
Keeping Things Discrete
Calculating probability distributions takes time.
So far we’ve looked at how to calculate and use probability distributions, but wouldn’t it be
nice to have something easier to work with, or just quicker to calculate? In this chapter,
we’ll show you some special probability distributions that follow very definite patterns.
Once you know these patterns, you’ll be able to use them to calculate probabilities,
expectations, and variances in record time. Read on, and we’ll introduce you to the
geometric, binomial and Poisson distributions.
Calculating probability distributions takes time.
So far we’ve looked at how to calculate and use probability distributions, but wouldn’t it be
nice to have something easier to work with, or just quicker to calculate? In this chapter,
we’ll show you some special probability distributions that follow very definite patterns.
Once you know these patterns, you’ll be able to use them to calculate probabilities,
expectations, and variances in record time. Read on, and we’ll introduce you to the
geometric, binomial and Poisson distributions.
270 Chapter 7
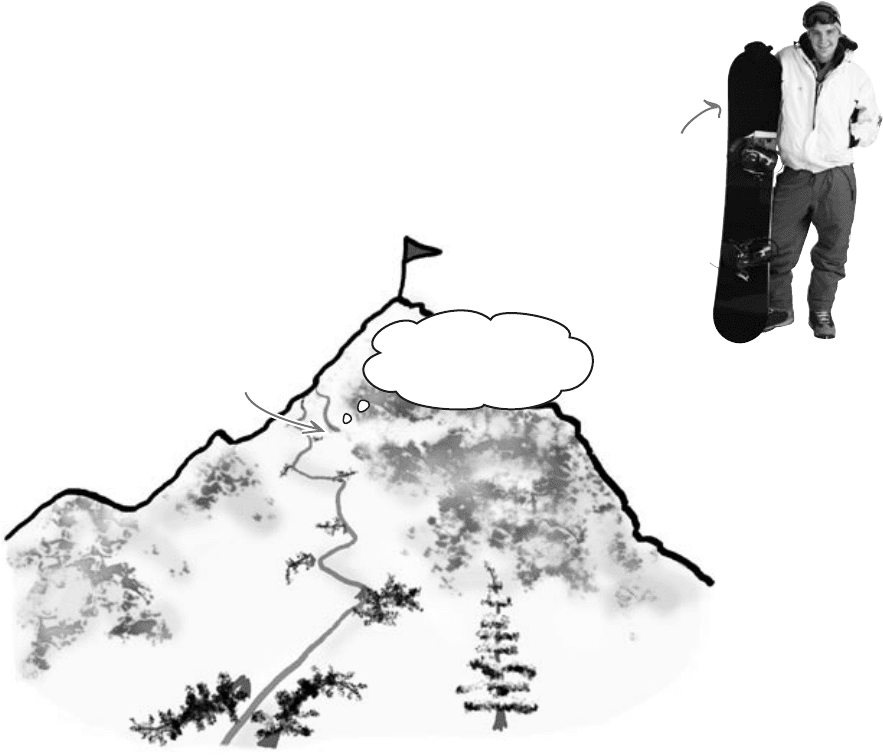
Meet Chad, the hapless snowboarder
Chad likes to snowboard, but he’s accident-prone. If there’s a lone
tree on the slopes, you can guarantee it will be right in his path. Chad
wishes he didn’t keep hitting trees and falling over; his insurance is
costing him a fortune.
Ouch! Rock! Ouch!
Flag! Ouch! Tree!
Chad’s about here—just
follow the tree damage
to see how well his first
run went.
There’s a lot riding on Chad’s performance on the slopes: his ego, his
success with the ski bunnies on the trail, his insurance premiums. If it’s
likely he’ll make it down the slopes in less than 10 tries, he’s willing to
risk embarrassment, broken bones, and a high insurance deductible to
try out some new snowboarding tricks.
The probability of Chad making a clear run down the slope is 0.2, and
he’s going to keep on trying until he succeeds. After he’s made his first
successful run down the slopes, he’s going to stop snowboarding, and
head back to the lodge triumphantly.
Chad
watch out for that tree!
