Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 291

What are the probabilities for this problem? What sort of pattern

can you see? We’re using X to represent the number of questions

you get correct out of three.

x P(X = x) Power of 0.75 Power of 0.25

0 0.75

3 0

Should you play, or walk away?

It’s unlikely you’ll know the game show host well enough to answer these

questions, so let’s see if we can find the probability distribution for the number

of questions you’ll get correct if you choose answers at random. That should

help you decide whether or not to play on.

Here’s a probability tree for the three questions:

Incorrect

Correct

0.75

0.25

Incorrect

Correct

0.75

0.25

Correct

0.75

0.25

Incorrect

Correct

0.75

0.25

Correct

0.75

0.25

Correct

0.75

0.25

Correct

0.75

0.25

Question 1

Question 2

Question 3

292 WHO WANTS TO WIN A SWIVEL CHAIR

0.75

x P(X = x) Power of 0.75 Power of 0.25

0.75

= .422

3 0

3 x 0.75

x 0.25 = .422 2 1

3 x 0.75 x 0.25

= .141 1 2

0.25

= .015 0 3

Incorrect

Correct

0.75

0.25

Incorrect

Correct

0.75

0.25

Correct

0.75

0.25

Incorrect

Correct

0.25

Correct

0.75

0.25

Correct

0.75

0.25

Correct

0.75

0.25

Question 1

Question 2

Question 3

What are the probabilities for this problem? What sort of pattern

can you see? We’re using X to represent the number of questions

you get correct out of three.

Think back to when you looked at permutations

and combinations in Chapter 6. How do you think

they might help you with this sort of problem?

There are 3

different ways

you can get one

question right, and

all of them have

a probability of

0.75

x 0.25.

You’ve got a 42% chance of

getting one question right, and a

14% chance of getting two right.

Those aren’t bad odds. I suggest

you go for it and guess.

you are here 4 293

P(X = r) = ?

0.25

0.75

3 - r

So far we’ve looked at the probability distribution of X, the number of

questions we answer correctly out of three.

Just as with the geometric distribution, there seems to be a pattern in

the way the probabilities are formed. Each probability contains different

powers of 0.75 and 0.25. As x increases, the power of 0.75 decreases

while the power of 0.25 increases.

In general, P(X = r) is given by:

In other words, to find the probability of getting exactly r questions right,

we calculate 0.25

, multiply it by 0.75

3-r

, and then multiply the whole lot by

some number. But what?

The probability of getting a question right

The probability of getting a question wrong

There are 3 questions

r is the number of

questions we get right

What’s the missing number?

For each probability, we need to answer a certain number of questions

correctly, and there are different ways of achieving this. As an example,

there are three different ways of answering exactly one question correctly

out of three questions. Another way of looking at this is that there are 3

different combinations.

Just to remind you, a combination

is the number of ways of choosing r

objects from n, without needing to know the exact order. This is exactly the

situation we have here. We need to choose r correct questions from 3.

This means that the probability of getting r questions correct out of 3 is

given by

P(X = r) =

0.25

0.75

3 - r

What’s this?

We covered this back in Chapter 6;

look back if you need a reminder.

Generalizing the probability for three questions

Let’s see how well

you did in Round

One, “All About Me.”

So, by this formula, the probability of getting 1 question

correct is:

P(X = r) =

0.25

0.75

3 - 1

= 3!/(3-1)!

0.25

0.5625

= 6/2

0.0625

0.75

=0.422

This is the same result we got using

our chart on the previous page.

294 WHO WANTS TO WIN A SWIVEL CHAIR

Here are the questions for Round One. The questions are all

about the game show host.

Looks like you tied

with another contender.

Congratulations, you’re

through to the next round.

D: Intelligence

B: Charm

C: Sense of Humor

3. What do people like most about him?

A: Good looks

D: April

B: February

C: March

2. In what month is his birthday?

A: January

D: Yellow

B: Blue

C: Green

1. What’s his favorite color?

A: Red

you are here 4 295

It looks like these questions are just as obscure as the ones in the previous round, so

you’ll have to answer questions at random again.

Let’s see if we can work out the probability distribution for this new set of questions.

Here are the questions for Round Two. The

questions are all about the game show host.

D: Releasing an album

B: Winning Mr Statsville 2008

C: Raising $1000 for the seal sanctuary

3. What is his greatest achievement?

A: Hosting a quiz show

D: A hovercraft

B: A tin dog

C: A horse

2. What would be an ideal gift for him?

A: A statue

D: May

B: Marie

C: Maggie

1. What was the name of his first girlfriend?

A: Mary

D: To have his own hair care range

B: To release an exercise DVD

C: To launch his own range of menswear

4. What is his secret ambition?

A: To launch a range of sports equipment

D: 2008

B: 2006

C: 2007

5. In what year was he abducted by aliens?

A: 2005

Round Two of Who Wants To Win A Swivel Chair

is called “More About Me.” This time I’ll ask you five

questions. As before, there are four possible answers

to each question. Do you want to play on?

296 WHO WANTS TO WIN A SWIVEL CHAIR

Let’s generalize the probability further

So far you’ve seen that the probability of getting r questions correct out

of 3 is given by

where the probability of answering a question correctly is 0.25, and the

probability of answering incorrectly is 0.75.

The next round of Who Wants To Win A Swivel Chair has 5 questions

instead of 3. Rather than rework this probability for 5 questions, let’s

rework it for n questions instead. That way we’ll be able to use the same

formula for every round of Who Wants To Win A Swivel Chair.

So what’s the formula for the probability of getting r questions right out of

n? It’s actually

What if the probability of getting a

question right changes? I wonder if we

can generalize this further.

P(X = r) =

n - r

This sort of problem is called the binomial distribution. Let’s take a

closer look.

P(X = r) =

0.25

0.75

3 - r

P(X = r) =

0.25

0.75

n - r

Yes, we can generalize this further.

Imagine the probability of getting a question right is given by p, and

the probability of getting a question wrong is given by 1 – p, or q. The

probability of getting r questions right out of n is given by

Just replace the 3 with n.

you are here 4 297

Guessing the answers to the questions on Who Wants To Win A Swivel

Chair is an example of the binomial distribution. The binomial

distribution covers situations where

P(X = r) =

n - r

p is the probability of a successful outcome in each trial, and n is the number

of trials. We can write this as

You’re running a series of independent trials.

There can be either a success or failure for each trial, and the

probability of success is the same for each trial.

There are a finite number of trials.

These two are like the

Geometric distribution.

Just like the geometric distribution, you’re running a series of independent

trials, and each one can result in success or failure. The difference is that

this time you’re interested in the number of successes.

Let’s use the variable X to represent the number of successful

outcomes out of n trials. To find the probability there are r successes,

use:

X ~ B(n, p)

This is different.

= n!

r! (n - r)!

Binomial Distribution Up Close

where

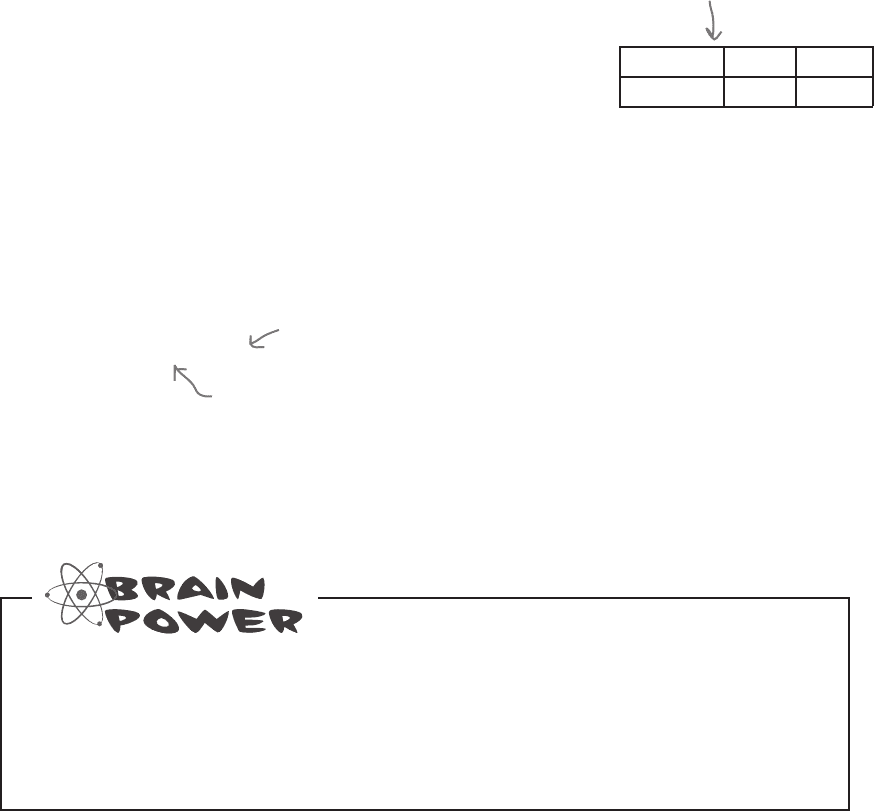
The exact shape of the binomial distribution varies

according to the values of n and p. The closer to 0.5 p is,

the more symmetrical the shape becomes. In general it is

skewed to the right when p is below 0.5, and skewed to the

left when p is greater than 0.5.

The shape of the binomial

distribution depends on the

values of n and p.

P(X = x)

298 WHO WANTS TO WIN A SWIVEL CHAIR

What’s the expectation and variance?

So far we’ve looked at how to use the binomial distribution to find basic

probabilities, which allows us to calculate the probability of getting a certain

number of questions correct. But how many questions can we actually expect to

get right if we choose the answers at random? That will help you better decide

whether we should answer the next round of questions.

Let’s see if we can find a general expression for the expectation and variance.

We’ll start by working out the expectation and variance for a single trial, and then

see if we can extend it to n independent trials.

x 0 1

P(X = x)

q p

Let’s look at one trial

Suppose we conduct just one trial. Each trial can only result in success or

failure, so in one trial, it’s possible to have 0 or 1 successes. If X ~ B(1, p),

the probability of 1 success is p, and the probability of 0 successes is q.

We can use this to find the expectation and variance of X. Let’s start with the expectation.

E(X) = 0q + 1p

= p

Var(X) = E(X

) - E(X)

= (0q + 1p) - p

= p - p

= p(1 - p)

= pq

So for a single trial, E(X) = p and Var(X) = pq. But what if there are n trials?

E(X

)

E(X) = p, so E(X)

= p

This is the probability distribution

of X where X ~ B(1, p).

In general, what happens to the expectation and variance when there are n

independent observations? How can this help us now?

you are here 4 299

Pool Puzzle

Let’s see if you can derive the expectation

and variance for Y ~ B(n, p). Your job

is to take elements from the pool

and place them into the blank lines

of the calculations. You may not

use the same element more than

once, and you won’t need to use all

the elements.

Note: each element in

the pool can only be

used once!

E(X) = E(X

) + E(X

) + ... + E(X

)

= E(X

)

Hint: Each X

is a separate trial. E(X

) = p,

and Var(X

) = pq

You need to find the expectation and variance

of n independent trials.

Var(X) = Var(X

) + Var(X

) + ... + Var(X

)

= Var(X

)

npq

300 WHO WANTS TO WIN A SWIVEL CHAIR

Pool Puzzle Solution

Let’s see if you can derive the expectation

and variance for Y ~ B(n, p). Your job

is to take elements from the pool

and place them into the blank lines

of the calculations. You may not

use the same element more than

once, and you won’t need to use all

the elements.

E(X) = E(X

) + E(X

) + ... + E(X

)

= E(X

)

Hint: Each X

is a separate trial. E(X

) = p,

and Var(X

) = pq

You need to find the expectation and variance

of n independent trials.

r(X) = Var(X

) + Var(X

) + ... + Var(X

)

= Var(X

)

npq

If X ~ B(n, p), then

E(X) = np

Var(X) = npq

You didn’t need

these elements.

Since the trials are independent, E(X

) = E(X

and so on.

Since the trials are independent,

Var(X

) = Var(X

), and so on.