Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 271

geometric, binomial, and poisson distributions

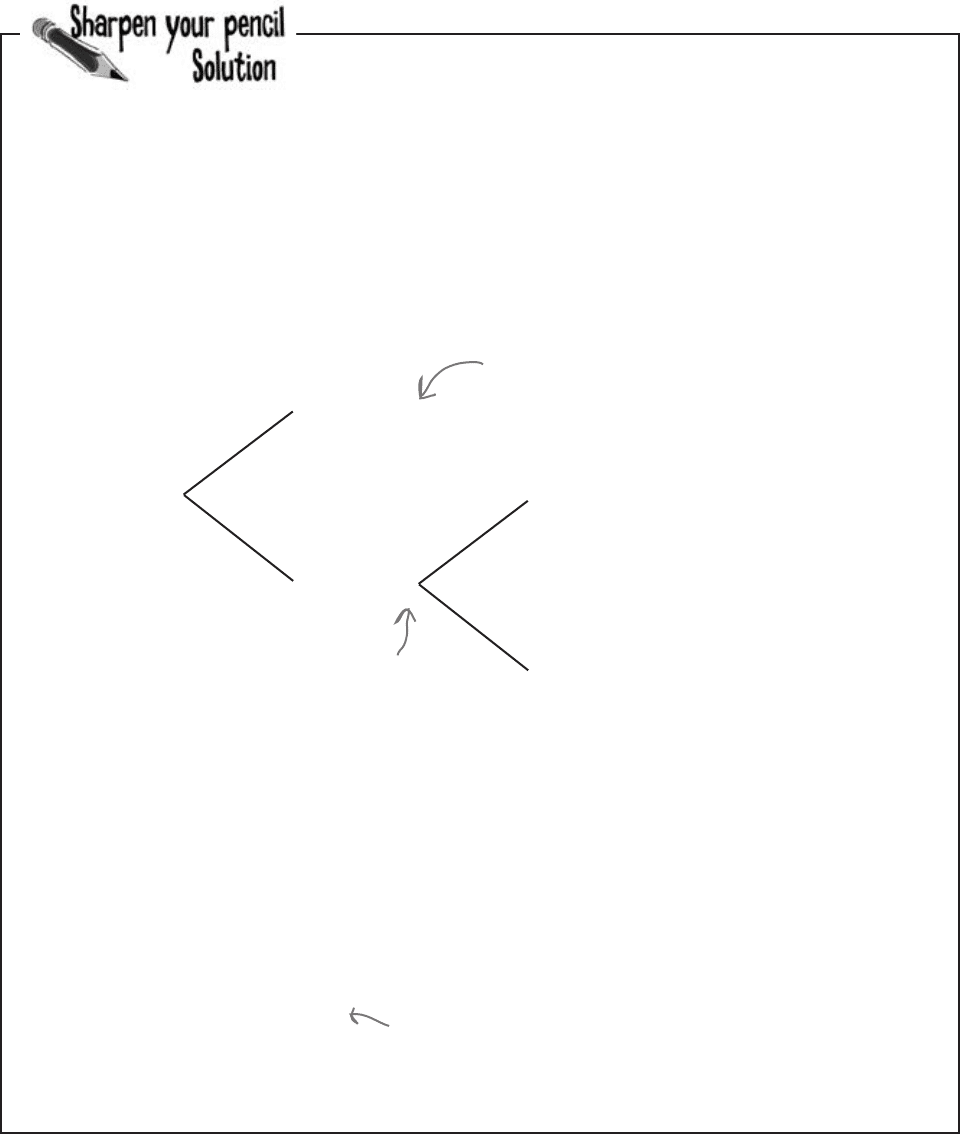
It’s time to exercise your probability skills. The probability of Chad

making a successful run down the slopes is 0.2 for any given trial

(assume trials are independent). What’s the probability he’ll need

two trials? What’s the probability he’ll make a successful run down

the slope in one or two trials? Remember, when he’s had his first

successful run, he’s going to stop.

Hint: You may want to draw a

probability tree to help visualize

the problem.

Chad is remarkably resilient,

and any collisions in a given run

don’t affect his performance in

future trials.

272 Chapter 7

It’s time to exercise your probability skills. The probability of Chad

making a successful run down the slopes is 0.2 for any given trial

(assume trials are independent). What’s the probability he’ll need

two trials? What’s the probability he’ll make a successful run down

the slope in one or two trials? Remember, when he’s had his first

successful run, he’s going to stop..

Success

Fail

0.2

0.8

Trial 1

Success

Fail

0.2

0.8

Trial 2

As soon as Chad makes

a successful run down

the slope, he’ll stop.

Chad fails on his

first attempt, so he

tries again.

Here’s a probability tree for the first two trials, as these are all that’s needed to work out the

probabilities.

If we say X is the number of trials needed to get down the slopes, then

P(X = 1) = P(Success in trial 1)

= 0.2

P(X = 2) = P(Success in trial 2 ∩ Failure in trial 1)

= 0.2 x 0.8

= 0.16

P(X ≤ 2) = P(X = 1) + P(X = 2)

= 0.2+0.16

= 0.36

We can add these

probabilities because

they’re independent.

sharpen solution

you are here 4 273

geometric, binomial, and poisson distributions

Hang on. If we have to work

out every single probability, we’ll

be here forever.

So you expect me to come up

with the probability distribution

of something that’s neverending? Is

that your idea of a joke?

There’s a problem because the number of possibilities

is neverending.

Chad will continue with his attempts to make it down the slope until he is

successful. This could take him 1 attempt, 10 attempts, 100 attempts, or

even 1,000 attempts. There are no guarantees about exactly when Chad

will first successfully make it down the slopes.

Even though it’s neverending, there’s still a way of

figuring out this type of probability distribution.

This is actually a special kind of probability distribution, with special

properties that makes it easy to calculate probabilities, along with the

expectation and variance.

Let’s see if we can figure it out.

So far you’ve found the probability that Chad will need fewer than three

attempts to make it down the slope. But what if you needed to look at the

probability of him needing fewer than 10 attempts (for insurance reasons),

or even 20 or 100?

Rather than work out the probabilities from scratch every time, it would

be useful if we could use a probability distribution. To do this, we need

to work out the probability for every single possible number of attempts

Chad needs to get down the slope.

We need to find Chad’s probability distribution

274 Chapter 7

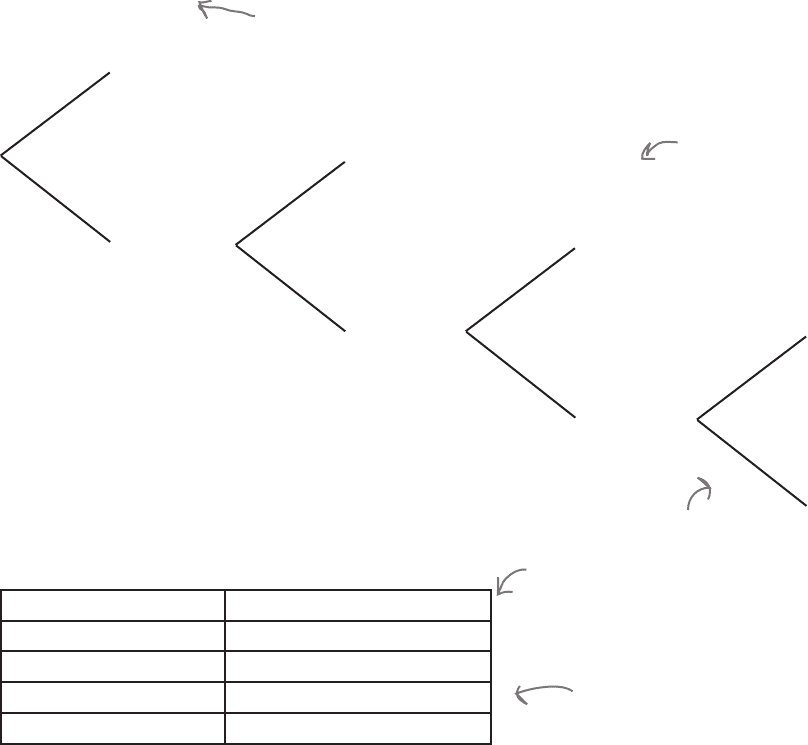
Let’s define the variable X to be the number of trials needed for

Chad to make a successful run down the slope. Chad only needs

to make one successful run, and then he’ll stop.

Let’s start off by examining the first four trials so that we can

calculate probabilities for the first four values of X. By doing this,

we can see if there’s some sort of pattern that will help us to easily

work out the probabilities of other values.

Success

Fail

0.2

0.8

Trial 1

Success

Fail

0.2

0.8

Trial 2

Success

Fail

0.2

0.8

Trial 3

Success

Fail

0.2

0.8

Trial 4

Here are the probabilities for the first four values

of X.

...

P(X = 1) is the

probability of Chad

being successful in

trial 1.

x P(X = x)

1 0.2

2 0.8

0.2 = 0.16

3 0.8

0.8

0.2 = 0.128

4 0.8

0.8

0.2 = 0.1024

P(X = 3) is the probability

of Chad being successful

in trial 3—that is, failing

in the first two trials, but

being successful in the third.

These probabilities are

calculated using the

probability tree.

There’s a pattern to this probability distribution

Notice each probability is

composed by multiplying

different powers of 0.8 and

0.2 together.

chad’s probability tree

you are here 4 275

geometric, binomial, and poisson distributions

Here’s a table containing the the probabilities of X for different values. Complete the table, filling

out the probability that there will be x number of trials, and indicating what the power of 0.8 and

0.2 are in each case (the number of times.0.8 and 0.2 appear in P(X = x)).

x P(X = x) Power of 0.8 Power of 0.2

0.2 0 1

0.8

0.2 1 1

0.8

0.2 2

r is a particular value of x but

we’re not saying which one. Can you

guess what the probability will be in

terms of r?

We’ve left extra space here for your calculations.

276 Chapter 7

They refer to two different things.

When we use P(X = x), we’re using it to demonstrate x taking on any value

in the probability distribution. In the table above, we show various values

of x, and we calculate the probability of getting each of these values.

When we use P(X = r), x takes on the particular value r. We’re looking

for the probability of getting this specific value. It’s just that we haven’t

specified what the value of r is so that we can come up with a generalized

calculation for the probability.

It’s a bit like saying that x can take on any value, including the fixed value r.

Here’s a table containing the the probabilities of X for different values. Complete the table, filling

out the probability that there will be x number of trials, and indicating what the power of 0.8 and

0.2 are in each case (the number of times.0.8 and 0.2 appear in P(X = x)).

x P(X = x) Power of 0.8 Power of 0.2

0.2 0 1

0.8

0.2 1 1

0.8

0.2 2

0.8

x 0.2 3 1

0.8

x 0.2 4 1

0.8

r-1

x 0.2 r - 1 1

For X = 4, Chad fails three times and succeeds on his fourth attempt.

P(X = 4) is therefore 0.8 x 0.8 x 0.8 x 0.2, as the probability of failing on a particular run is 0.8 and the

probability of success is 0.2.

For X = 5, Chad fails on his first four attempts. and succeeds on his fifth. This means

P(X = 5) = 0.8 x 0.8 x 0.8 x 0.8 x 0.2.

So what if P(X = r)? For Chad to be successful on his r’th attempt, he must have failed in his first (r-1)

attempts, before succeeding in his r’th. Therefore

P(X = r) = 0.8 x 0.8 x ... x 0.8 x 0.2, which means that in our expression, 0.8 is taken to the (r-1)th power.

First you say P(X = x),

then you say P(X = r). I wish

you’d make your mind up.

exercise solution

you are here 4 277

geometric, binomial, and poisson distributions

As you can see, the probabilities of Chad’s snowboarding trials follow a

particular pattern. Each probability consists of multiples of 0.8 and 0.2.

You can quickly work out the probabilities for any value r by using:

P(X = r) = 0.8

r-1

0.2

In other words, if you want to find P(X = 100), you don’t have to draw an

enormous probability tree to work out the probability, or think your way

through exactly what happens in every trial. Instead, you can use:

P(X = 100) = 0.8

0.2

We can generalize this even further. If the probability of success in a trial

is represented by p and the probability of failure is 1 - p, which we’ll call

q, we can work out any probability of this nature by using:

P(X = r) = q

r - 1

This formula is called the geometric distribution.

I’m a failure <sniff>

q is equal to 1 - p. If p

represents the probability

of success, then q represents

the probability of failure.

What’s the point in generalizing

this? It’s just one particular problem

we’re dealing with.

A: We’re generalizing it so that we can

apply the results to other similar problems. If

we can generalize the results for this kind of

problem, it will be quicker to use it for other

similar situations in the future.

You said we needed to find an

expression for P(X = r). What’s r?

A: P(X = r) means “the probability that X

is equal to value r,” where r is the number of

trials we need to get the first success.

If you wanted to find, say, P(X = 20), you

could substitute r for 20. This would give you

a quick way of finding the probability.

Why is it the letter r? Why not some

other letter?

A: We used the letter r so that we could

generalize the result for any particular

number. We could have used practically any

other letter, but using r is common.

How can we have a probability

distribution if the number of possibilities

is endless?

A: We don’t have to specify a probability

distribution by physically listing the

probability of every possible outcome. The

key thing is that we need a way of describing

every possibility, which we can do with a

formula for computing the probability.

Wouldn’t Chad’s snowboarding

skills eventually improve? Is it realistic to

say the probability of success is 0.2 for

every trial?

A: That may be a fair assumption. But

in this problem, Chad is truly hapless when

it comes to snowboarding, and we have to

assume that his skills won’t improve—which

means his probability of success on the

slopes will follow the geometric distribution.

(r - 1) failures and 1 success.

In our case, p = 0.2 and

q = 0.8.

The probability distribution can be represented algebraically

278 Chapter 7

P(X = r) = p q

r - 1

Let’s use the variable X to represent the number of trials needed to

get the first successful outcome—in other words, the number of trials

needed for the event we’re interested in to happen.

To find the probability of X taking a particular value r, you can get a quick

result by using:

You run a series of independent trials.

There can be either a success or failure for each trial, and the

probability of success is the same for each trial.

The main thing you’re interested in is how many trials are needed in

order to get the first successful outcome.

where p is the probability of success, and q = 1 – p, the probability of failure.

In other words, to get a success on the rth attempt, there must first have been

(r – 1) failures.

So if you have a situation that matches this set of criteria, you can use the

geometric distribution to help you take a few shortcuts. The important thing

to be aware of is that we use the word “success” to mean that the event

we’re interested in happens. If we’re looking for an event that has negative

connotations, in statistical terms it’s still counted as a success.

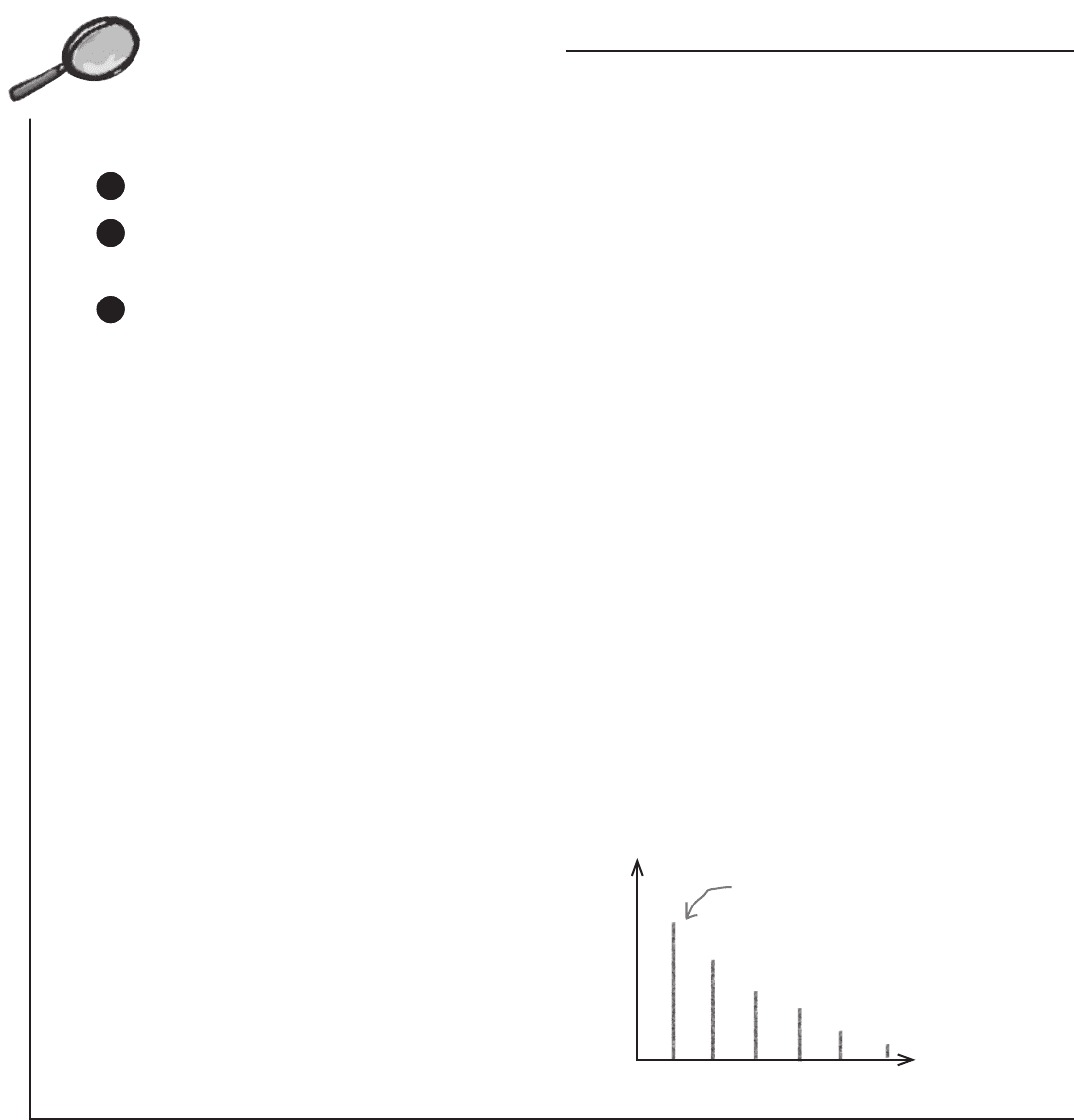
The geometric distribution has a distinctive shape.

P(X = r) is at its highest when r = 1, and it gets lower and

lower as r increases. Notice that the probability of getting

a success is highest for the first trial. This means that the

mode of any geometric distribution is always 1,

as this is the value with the highest probability.

This may sound counterintuitive, but it’s most likely that

only one attempt will be needed for a successful outcome.

Geometric Distribution Up Close

We said that Chad’s snowboarding exploits are an example of the geometric

distribution. The geometric distribution covers situations where:

This is the general shape of

the geometric distribution.

The mode is always 1.

P(X = x)

geometric distribution in depth

you are here 4 279

geometric, binomial, and poisson distributions

X ~ Geo(p)

P(X ≤ r) = 1 - q

P(X > r) = q

We can use this to find P(X r), the probability that r or fewer trials are

needed in order for there to be a successful outcome.

If we add together P(X r) and P(X > r), the total must be 1. This means that

If a variable X follows a geometric distribution where the probability of

success in a trial is p, this can be written as

As well as finding exact probabilities for the geometric distribution, there’s also

a quick way of finding probabilities that deal with inequalities.

Let’s start with P(X > r).

P(X > r) is the probability that more than r trials will be needed in order to get

the first successful outcome. In order for more than r trials to be needed, this

means that the first r trials must have ended in failure. This means that you

find the probability by multiplying the probability of failure together r times.

For the number of trials needed for a success to be greater

than r, there must have been r failures.

P(X r) + P(X > r) = 1

P(X r) = 1 - P(X > r)

This gives us

This is because P(X ≤ r) is the opposite of P(X > r).

P(X ≤ r) = 1 - P(X > r).

This is a quick way of saying “X follows a geometric

distribution where the probability of success is p.”

I’m getting bruised! How

many attempts do you

expect me to have to make

before I make it down the

slope OK?

The geometric distribution also works with inequalities

From above, we know that P(X > r).=q

so we substitute in q

for P(X > r) to

get this formula.

We don’t need p in this formula because

we don’t need to know exactly which trial

was successful, just that there must be

more than r trials.

280 Chapter 7

So far we’ve found probabilities for the number of attempts Chad

needs to make before successfully makes it down the slope, but what

if we want to find the expectation and variance? If we know the

expectation, for instance, we’ll be able to say how many attempts we

expect Chad to make before he’s successful.

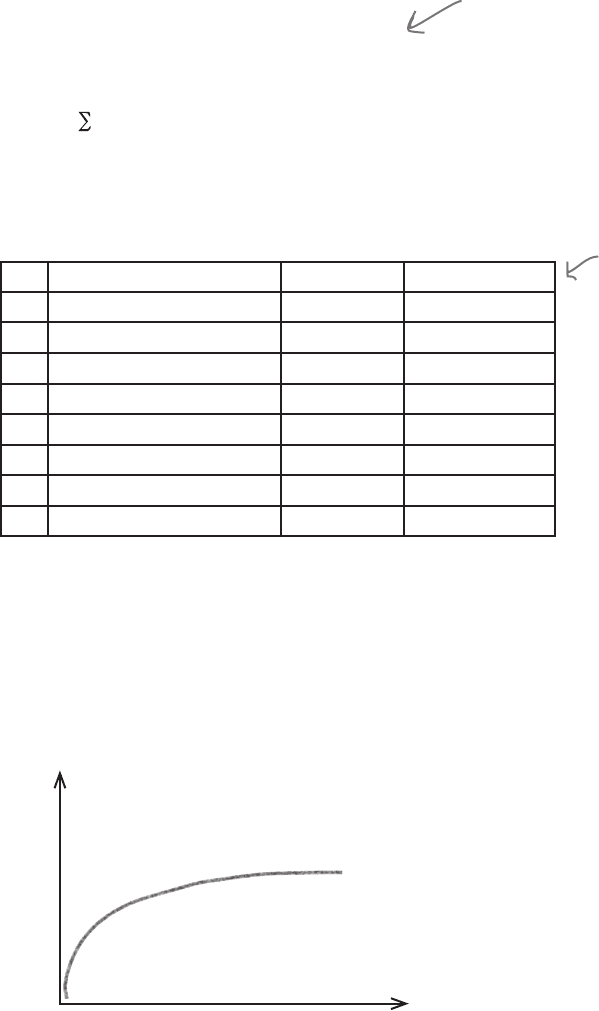
Can you remember how we found expectations earlier in the book?

We find E(X) by calculating xP(X = x). The probabilities in this

case go on forever, but let’s start by working out the first few values to

see if there’s some sort of pattern.

Here are the first few values of x, where X ~ Geo(0.2)

Can you see what happens to the values of xP(X = x)?

The values of xP(X = x) start off small, and then they get larger until x = 5. When

x is larger than 5, the values start decreasing again, and keep on decreasing as x

gets larger. As x gets larger, xP(X = x) becomes smaller and smaller until it makes

virtually no difference to the running total.

We can see this more clearly if we chart the cumulative total of xP(X = x):

x P(X = x) xP(X = x) xP(X ≤ x)

1 0.2 0.2 0.2

2 0.8

0.2 = 0.16 0.32 0.52

3 0.8

0.2 = 0.128 0.384 0.904

4 0.8

0.2 = 0.1024 0.4096 1.3136

5 0.8

0.2 = 0.08192 0.4096 1.7232

6 0.8

0.2 = 0.065536 0.393216 2.116416

7 0.8

0.2 = 0.0524288 0.3670016 2.4834176

8 0.8

0.2 = 0.04194304 0.33554432 2.81894608

This is the running total of

xP(X = x)

ΣxP(X ≤ x)

As a reminder, expectation is the average

value that you expect to get, a bit like the

mean but for probability distributions.

Variance is a measure of how much you can

expect this to varies by.

The pattern of expectations for the geometric distribution

geometric expectation