Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

higher temperature, about 1200 K. This feature was explained

[52]

by the

contribution of short-circuit diffusion, since polycrystalline material was

used. Frank et al.

[53]

thoroughly measured Ni self-diffusion, combining the

tracer technique at higher temperatures and the SIMS analysis at lower

ones in poly- and single-crystalline Ni

Al, respectively. No curvature of

the Arrhenius plot was established [see Fig. 4.8(a)], confirming the expla-

nation given by Shi et al.

[52]

These data indicate that only one diffusion

mechanism operates in the temperature interval under consideration. This

mechanism is commonly identified with the Ni-sublattice diffusion mech-

anism.

[52, 53]

According to this mechanism, a Ni vacancy performs random

jumps in the Ni sublattice with the coordination number 8 (see Fig. 4.5).

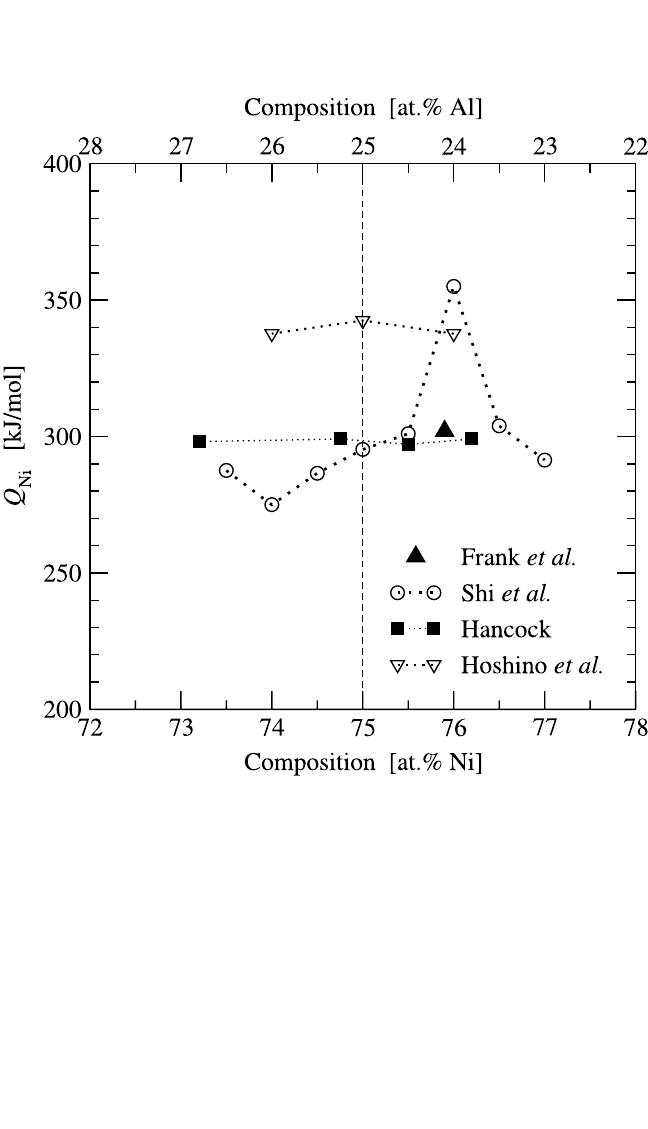
Some controversy still exists about the compositional dependence of

Ni self-diffusion in Ni

Al (Fig. 4.9). Hoshino et al.

[51]

have found a shal-

low minimum of D

at the stoichiometric composition below T  1100 K.

Shi et al.

[52]

also observed such a minimum in D

, but around 76 at.% Ni

and, again, at the lowest temperature of their investigations, about 1200 K.

At higher temperatures, the variation of D

with composition in all inves-

tigations was within experimental uncertainities. These fine features

resulted in a maximum activation enthalpy Q

at about 76 at.% Ni

[52]

(Fig. 4.9). Since Ni grain boundary diffusion in Ni

Al shows a deep min-

imum at the stoichiometric composition, Frank and Herzig

[55]

suggested

that short-circuit diffusion via grain boundaries affected the low-temperature

data of Hoshino et al.

[51]

and Shi et al.,

[52]

and produced a slight minimum

in the bulk diffusion data. Comparing results of different investigations,

Fig. 4.9 suggests that the change of the activation enthalpy Q

with com-

position in Ni

Al is within experimental uncertainties. In contrast, a min-

imum in D

was found in a recent Monte Carlo study of Ni diffusion in

Al at the stoichiometric composition

[56]

due to the existence of Al and

Ni antistructure atoms in Ni- and Al-rich alloys, which enhance Ni self-

diffusion by lowering the energy barriers for the Ni vacancy jumps. In that

approach, pair interaction potentials were used and no lattice relaxation

was taken into account.

For additional insight into this problem, we simulated self-diffusion

in Ni

Al using the Voter and Chen EAM potentials.

[24]

The calculations

show that there is a negligible effect of adjacent Ni and Al antistructure

atoms on the energy barriers for Ni vacancies performing jumps via the

Ni sublattice. (The energy barriers change by about 10 kJ/mol, depend-

ing on the particular configuration.) Thus, the vacancy jump rates are

nearly the same, regardless of the composition of Ni

Al. Calculations of

the Ni vacancy concentration [Fig. 4.3(c)] and the effective formation

energies also resulted in very similar values for Al-rich, stoichiometric,

and Ni-rich compounds. Simultaneous Monte Carlo simulations of the

correlation effects demonstrated that the correlation factor for the Ni

192 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Chapter-04.qxd 11/29/04 6:36 PM Page 192

DIFFUSION IN INTERMETALLIC COMPOUNDS, HERZIG, DIVINSKI 193

sublattice diffusion mechanism across the stoichiometry changes negligi-

bly and equals about 0.689. These calculations support the conclusion that

Ni self-diffusion reveals only a marginal compositional dependence in

Al.

[53]

From the experimental point of view, Ni diffusion in the Ni

phase can be presented by a unique Arrhenius line with the parameters

given in Table 4.1.

Al Diffusion.

Al radiotracer diffusion in Ni

Al was measured

[41]

temperatures between 1273 and 1473 K. Unfortunately, the absolute val-

ues of Al diffusion are considered to be unconvincing because there is a

Figure 4.9 Activation enthalpy Q

of Ni self-diffusion in Ni

Al as a function of com-

position (open circles,

[52]

triangle up,

[53]

triangles down,

[51]

and squares

[54]

Chapter-04.qxd 11/29/04 6:36 PM Page 193

194 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

substantial deviation of the simultaneously measured Ni self-diffusion

results from the data of Frank et al.

[53]

Incomplete consideration of short-

circuit diffusion in polycrystalline samples may be one possible reason

for such deviations. However, the ratio of Al and Ni diffusivities meas-

ured by Larikov et al.

[41]

is likely to be more reliable, and we can antici-

pate that Al and Ni diffuse with similar rates in Ni

Al in this temperature

interval.

The interdiffusion coefficient D

∼

accross the phase field of Ni

Al was

measured by two groups.

[57, 58]

The temperature dependence of D

∼

for stoi-

chiometric Ni

Al is presented in Fig. 4.8(a). Intrinsic diffusivities of Al

and Ni were determined between 1425 and 1523 K.

[59]

Analyzing the rel-

ative positions of the Kirkendall and Matano planes, Fujiwara and Horita

concluded that the ratio of Al and Ni tracer diffusivities is very close to

unity in this temperature interval,

[59]

supporting the finding of Larikov

et al.

[41]

In Fig 4.8(a), the estimated Al diffusion coefficients are compared

with the Ni self-diffusivity. On the other hand, the Al diffusivity was esti-

mated by Ikeda et al.

[57]

using the Darken-Manning equation [Eq. (3); see

Fig. 4.8(a)]. Their smaller values of D

with respect to Fujiwara and

Horita’s results

[59]

may stem from some uncertainty involved in the calcu-

lations of the product Φ S.

Similar to Ni tracer diffusion, the interdiffusion coefficient in Ni

reveals only a marginal compositional dependence, which remains within

Table 4.1. Arrhenius Parameters of Self-Diffusion and Solute Diffusion in

Composition D

Tracer (at.% Ni) (m

1

) (kJ/mol) Ref.

Ni 75 1.5  10

2

347 51

Ni 74.7 1.0  10

4

303 54

Ni 75.9 3.1  10

4

302 53

75 8  10

3

340

Ga 75.9 7.8  10

2

363 63

Ge 75.9 1.0  10

1

369 63

Ge 75 3.6  10

1

379 61

Nb 75.9 2.6  10

476 63

Ti 75.9 8.6  10

1

425 63

Mo 75.1 2.3  10

493 61

Fe 75.1 1.3  10

2

335 64

Estimation from the Al intrinsic diffusion data of Fujiwara and Horita

[59]

Chapter-04.qxd 11/29/04 6:36 PM Page 194

DIFFUSION IN INTERMETALLIC COMPOUNDS, HERZIG, DIVINSKI 195

the experimental uncertainties.

[59]

From this we conclude that the Al dif-

fusivity does not markedly depend on composition in Ni

Al.

4.4.1.2 Solute Diffusion

Since Ge and Ga occupy the Al sublattice in Ni

Al,

[60]

these tracer

atoms can be used as the substitute for the Al diffusion.

[38, 61]

The available

data are presented in Fig. 4.8(b). Their diffusivities follow very similar

and straight Arrhenius dependencies in Ni

Al, with an activation enthalpy

of about 60 kJ/mol larger than that of Ni self-diffusion. It is important that

Ga and Ge diffusion in Ni

Al is very close to the Al diffusivity estimated

from the interdiffusion data

[59]

[Fig. 4.8(b)]. We conclude that these solute

atoms are indeed useful to simulate Al diffusion in Ni

Al.

Figure 4.8(b) suggests D

 D

at lower temperatures. This relation

is reversed, however, at higher temperatures, T  1350 K, where D



. This trend can also be anticipated for Al diffusion [see Fig. 4.8(b)].

Such behavior cannot be understood in terms of the Ni sublattice diffusion

mechanism of the minority component, as suggested by Numakura

et al.

[35]

Indeed, the effectiveness of diffusion by this mechanism strongly

depends on the probability of finding an Al (or Al-substitute) atom on the

wrong Ni sublattice. Consequently, Al should diffuse slower than Ni, in

agreement with the so-called Cu

Au rule.

[62]

However, it was shown by

Divinski et al.

[38]

that the ASB diffusion mechanism provides an addi-

tional and strong contribution for Al atoms comparable to the Ni sublat-

tice diffusion mechanism and that D

can approach the D

values at high

temperatures, in accordance with the experimental findings of Fujiwara

and Horita

[59]

[Fig. 4.8(b)].

Tracer diffusion of Ti and Nb was investigated

[63]

[Fig. 4.8(b)]. In con-

trast to Ge and Ga diffusion, Ti and Nb reveal a distinctly smaller diffu-

sivity with a larger activation enthalpy. From the direction and extent of the

homogeneity range of the L1

phase in a ternary region, the site preference

for Ti and Nb in Ni

Al was estimated.

[60]

Because Ti and Nb atoms mainly

dissolve on Al positions in the L1

lattice, a diffusion process similar to that

of Al is to be expected. The difference in the activation enthalpies of self-

diffusion and diffusion of such solutes is related to the formation energy of

the solute atom at an antistructural position in the Ni sublattice.

[53]

In Fig. 4.8(b), the tracer diffusivities of Mo

[61]

and Fe

[64]

in Ni

Al are

also plotted, as functions of the inverse temperature. The solute diffusion

behavior in Ni

Al can be well systemized in terms of an interplay of intra-

sublattice (the Ni sublattice mechanism) and inter-sublattice (the ASB

mechanism) jumps.

[61]

The Arrhenius parameters of self- and solute diffu-

sion in Ni

Al are summarized in Table 4.1.

Chapter-04.qxd 11/29/04 6:36 PM Page 195

196 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

4.4.2 Ti

4.4.2.1 Self-Diffusion

Ti Diffusion. Self-diffusion and solute diffusion in Ti

Al was com-

prehensively analyzed in a recent review.

[8]

In an investigation of Ti self-

diffusion in the phase a

-Ti

Al,

[65]

several compositions were studied: 75,

72, 68, and 65 at.% Ti. Within experimental error, the diffusivities were

very similar, with a slight increase of D

with increasing Al content at the

lowest temperature investigated. The change of Al content produced only

a marginal effect in the activation enthalpy of self-diffusion, Q

, although

the tendency of an increase of Q

with increasing Al content was indi-

cated.

[65]

As a result, one master Arrhenius dependence for Ti self-diffusion

in a

-Ti

Al was suggested [Fig. 4.10(a)] with the Arrhenius parameters

given in Table 4.2.

Ti self-diffusion in Ti

Al can be interpreted within the framework of

the Ti-sublattice diffusion mechanism.

[65]

The experimental data suggest

that the compositional Ti or Al antistructure atoms change the energy bar-

riers for vacancy jumps on the Ti sublattice only slightly. Since the Ti

vacancy formation enthalpies are also very similar for the stoichiometric

and Al-rich alloys,

[8, 19]

the weak compositional dependence of D

in Ti

is not unexpected.

Al Diffusion. Interdiffusion in the a

-Ti

Al-phase field was stud-

ied,

[65, 66]

with good agreement of the deduced diffusion data, which

practically overlap in Fig. 4.10(a). Applying the Darken-Manning analy-

sis with S  1 [Eq. (3)], Fig. 4.10(a) presents the calculated Al diffusion

coefficient D

as a function of temperature. The thermodynamic factors

required for such calculations were calculated by the CALPHAD

Table 4.2. Arrhenius Parameters of Self-Diffusion and Solute Diffusion in

Tracer (m

1

) (kJ/mol) Ref.

Ti 2.24  10

5

288 65

2.3  10

1

394 65

Ga 6.3  10

5

315 68

Fe 2.0  10

3

277 70

Ni 1.8  10

5

195 70

Nb 3.2  10

4

339 70

Calculation from the Darken-Manning equation

Chapter-04.qxd 11/29/04 6:36 PM Page 196

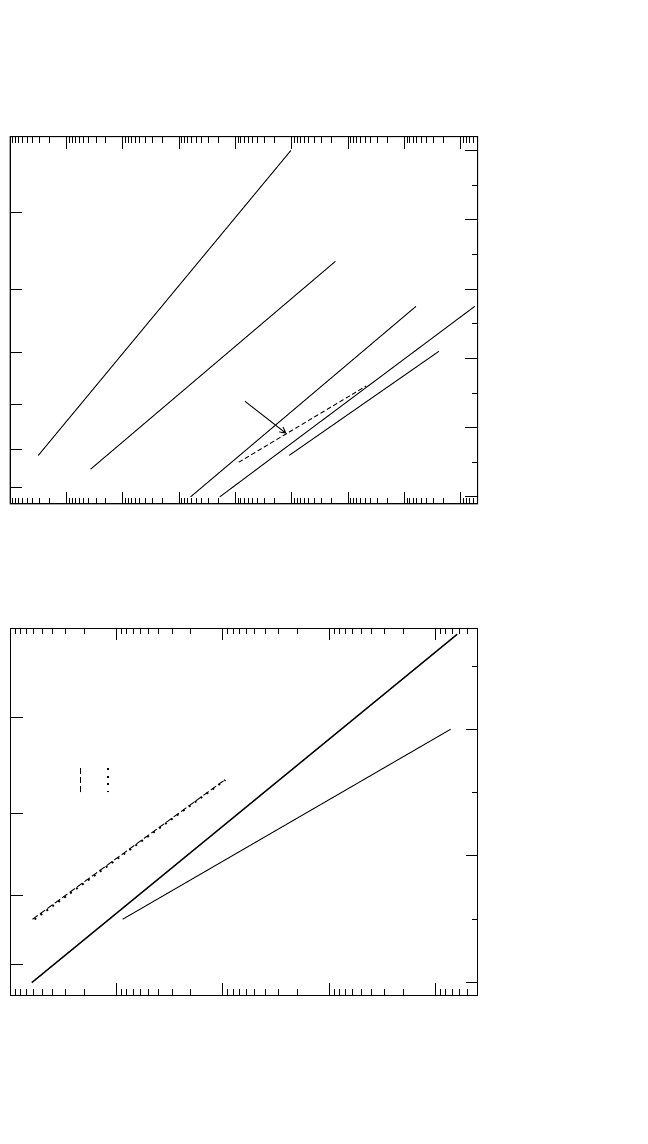
197

-1

[10

-4

-1

]

-19

-18

-17

-16

-15

, D [m

-1

]

Rüsing et al.

Sprengel et al.

1400 1300 1200 1100

T [K]

interdiffusion:

Figure 4.10 The Arrhenius plots of self-diffusion and solute diffusion in Ti

Al. In (a), the interdiffusion data D

∼

[66]

and

the estimated Al diffusivity

[65]

are plotted in comparison to Ti diffusion.

[65]

In (b), diffusion data for Ti,

[65]

Al,

[66]

Ga,

[68]

and

Nb, Fe, and Ni

[70]

diffusion are compared.

891011 12

-1

[10

-4

-1

]

-20

-19

-18

-17

-16

-15

-14

-13

-12

-1

]

1400 1300 1200 1100 1000

900

T [K]

(b) Solute Diffusion in Ti

(a) Self-Diffusion in Ti

Chapter-04.qxd 11/29/04 6:36 PM Page 197

198 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

method.

[67]

The weak compositional dependence of D

in Ti

Al is within

experimental error, but a slight increase with increasing Al content is

indicated.

[8]

The activation enthalpy Q

of Al diffusion ≈400 kJ/mol

(Table 4.2) turned out to be fairly large. The analysis of the experimen-

tal data suggests that the large value of Q

may be related to uncertain-

ties in the D

determination via the Darken relation, especially at low

temperatures.

[68]

4.4.2.2 Solute Diffusion

Since Ga occupies the Al sublattice in Ti

Al,

[69]

the study of Ga diffu-

sion is meaningful to obtain additional information on diffusion of an Al-

substituting solute in Ti

Al.

[68]

The measured Ga diffusion coefficients are

presented in Fig. 4.10(b) as a function of temperature. The figure indicates

that the absolute values of D

are similar to those of D

, but the activa-

tion enthalpy of Al diffusion is distinctly larger (see Table 4.2).

Ga diffusion in Ti

Al was interpreted in terms of the Ti-sublattice dif-

fusion mechanism of the minority component.

[68]

Thus, the excess of Q

with respect to Q

is related to the formation enthalpy of Ga atoms in anti-

structure positions on the Ti sublattice.

[68]

Due to the predominant vacancy

concentration in the Ti sublattice [Fig. 4.3(a)], Al is also expected to dif-

fuse predominantly as anti-structure atoms via the Ti sublattice. Thus we

regard the measured Q

value as realistic to represent Q

in Ti

Al.

Information is limited on diffusion of other solutes in a

-Ti

Al. Diffusion

of Nb in Ti

Al, studied

[70]

within the composition range from 27 to 33 at.%Al,

was found to be practically independent of composition. The corresponding

temperature dependence is presented in Fig. 4.10(b). Nb atoms occupy Ti sites

in Ti

Al.

[69]

Therefore, their diffusion is dominated by exchanges with vacan-

cies on the Ti sublattice (Ti-sublattice diffusion mechanism).

In view of the extremely fast diffusivity in a-Ti, diffusion of Fe and

Ni was investigated in Ti

Al.

[70]

Only a negligible compositional depend-

ence was observed, similar to the diffusion of Ga and Nb. The tempera-

ture dependencies obtained are presented in Fig. 4.10(b). This diagram

shows that Fe and Ni are also fast diffusers in Ti

Al, since their diffusivi-

ties exceed that of Ti self-diffusion by several orders of magnitude.

Fast diffusion of Fe and Ni in Ti

Al was explained

[8, 70]

by the disso-

ciative diffusion mechanism; that is, the diffusing atoms occupy both

interstitial and substitutional sites. In such a case, the effective diffusion

coefficient D is given by:

D  D

 D

 D

. (5)



 c



 c

Chapter-04.qxd 11/29/04 6:36 PM Page 198

DIFFUSION IN INTERMETALLIC COMPOUNDS, HERZIG, DIVINSKI 199

Here D

) is the interstitial (substitutional) diffusion coefficient, and

) is the interstitial (substitutional) solubility of the solute atoms.

Equation (5) was simplified under the plausible assumptions that c

 c

and c

 c

. Since c

and c

are temperature-dependent, the activa-

tion enthalpy of the dissociative diffusion can be remarkably larger than

that of pure interstitial diffusion. This conclusion agrees with the obser-

vation that the activation enthalpies of Fe and Ni diffusion (277 and

195 kJ/mol, respectively), in comparison with the Ti self-diffusion activa-

tion enthalpy (288 kJ/mol), are not as small as expected for the pure inter-

stitial diffusion mechanism.

4.4.3 TiAl

4.4.3.1 Self-Diffusion

Ti Diffusion. The self-diffusion behavior in Ni

Al and Ti

Al follows

almost ideal linear Arrhenius dependencies (see Figs. 4.8 and 4.10,

respectively), a behavior that is typical for the majority of intermetallic

phases. From a simplest point of view, such a behavior is somewhat unex-

pected in view of the variety of point defects and the number of possible

diffusion mechanisms in ordered intermetallics. However, the experimen-

tal data suggest that in many typical intermetallic phases, there is a given

diffusion mechanism that produces the main contribution to self-diffusion

and operates dominantly over a wide temperature interval. Astonishingly,

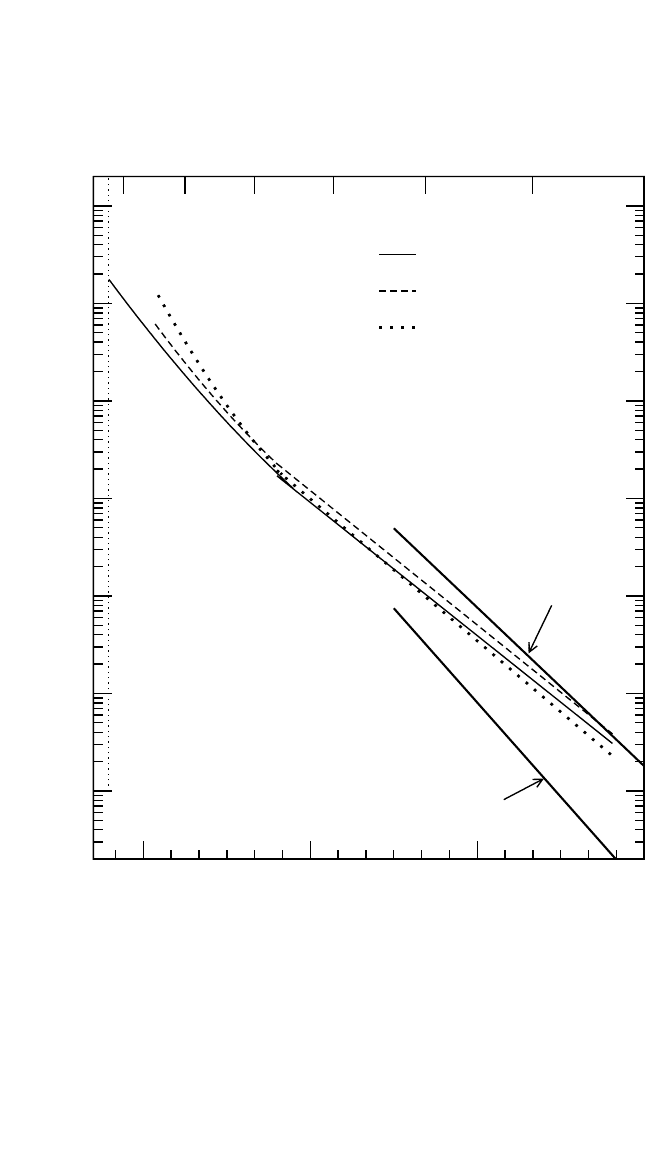
Ti self-diffusion in g-TiAl clearly revealed a non-Arrhenius character

[7]

[see Fig. 4.11(a)]. The Ti diffusivity follows an Arrhenius line up to about

T  1470 K, with a subsequent upward deviation to larger D

values at

higher temperatures. This effect was found to be almost independent of

the composition in TiAl.

[7]

Table 4.3 presents the activation enthalpy Q

of Ti-self diffusion in TiAl calculated by the Arrhenius fitting within the

temperature interval 1150 to 1470 K.

The pronounced curvature of Ti self-diffusion at T  1470 K is

explained by the additional effect of a second diffusion mechanism that

operates parallel to the Ti-sublattice mechanism.

[7]

In view of the high

concentration of Ti antistructure atoms, even in Al-rich compositions [see

Fig. 4.3(b)], the antistructure bridge mechanism [Fig. 4.7(b)] was pro-

posed to produce this additional contribution. The most important feature

of the ASB mechanism, when operating in the L1

structure of TiAl, is that

it reveals a nonpercolative nature and thus contributes at any concentra-

tion of the Ti antistructure atoms. This effect results from the interde-

pendence of the ASB mechanism with the simultaneous contribution of

the Ti-sublattice diffusion mechanism. Thus, in TiAl, the situation is very

different from that in the B2 compounds, where the percolation threshold

Chapter-04.qxd 11/29/04 6:36 PM Page 199

200 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

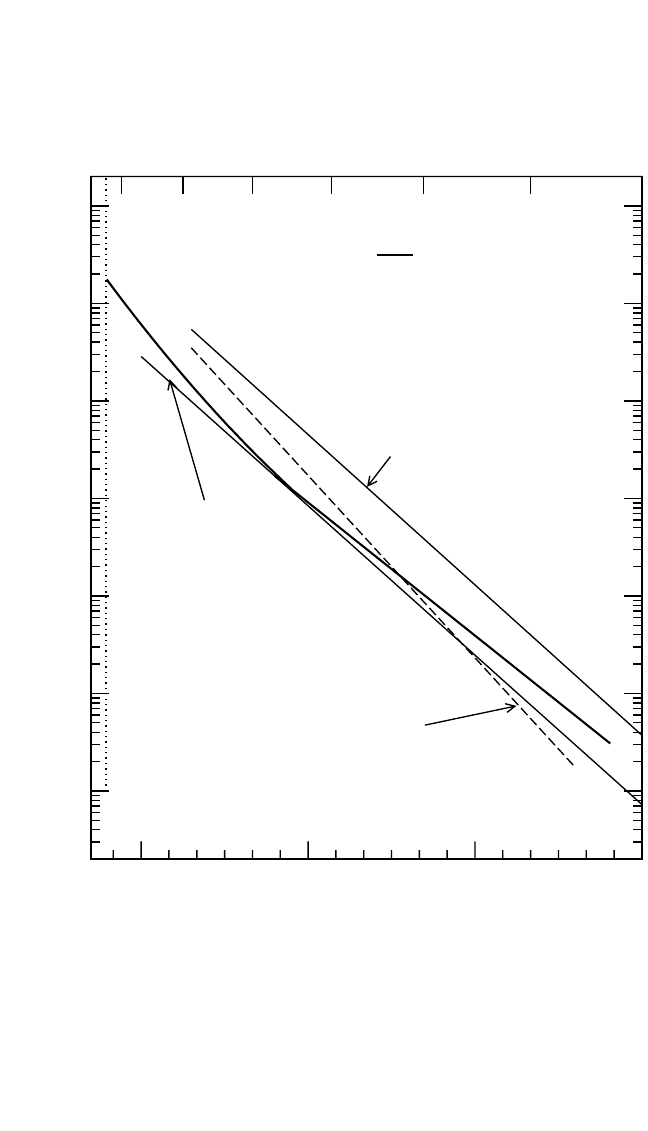
Figure 4.11 The Arrhenius presentation of Ti and Al component and solute diffu-

sion in TiAl. In (a), Ti self-diffusion in polycrystalline TiAl alloys of the indicated

compositions

[7]

is plotted in comparison to Ti diffusion along (D



) and perpendi-

cular (D

⊥

) to the Ti layers in the L1

structure of TiAl.

[71]

In (b), the interdiffusion

data,

[72]

estimated Al

[7]

and Ga

[68]

diffusivities are shown.In (c), Ti;

[7]

Nb, Zr, Fe, and

Ni;

[39]

and Co and Cr

[74]

diffusion is presented.

-1

[10

-4

-1

]

-18

-17

-16

-15

-14

-13

-12

-1

]

Ti in Ti

1500 1400 1300 120016001700

T [K]

⊥

(a) Ti Component in TiAl

Chapter-04.qxd 11/29/04 6:36 PM Page 200

DIFFUSION IN INTERMETALLIC COMPOUNDS, HERZIG, DIVINSKI 201

-1

[10

-4

-1

]

-18

-17

-16

-15

-14

-13

-12

, D [m

-1

]

Ti in Ti

1500 1400 1300 120016001700

T [K]

D (Sprengel et al.)

(b) Al Component in TiAl

Figure 4.11 (Continued)

Chapter-04.qxd 11/29/04 6:36 PM Page 201