Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.


Painleve' Equations and Associated Polynomials
139
the affine Weyl group
21,
which also is the transformation group for
PII
(Okamoto, 1986; Umemura, 2000; Umemura and Watanabe, 1997).
Ohyama (Ohyama, 2001) derived special polynomials associated with
the rational solutions of (3.12). These are essentially described in The-
orem
3.5
below, though here the variables have been scaled and the
expression of the rational solutions of (3.12) in terms of these special
polynomials is explicitly given.
Theorem
3.5.
Suppose that Rn(<) satisfies the recursion relation (Toda
equation)
with Ro(<)
=
1
and R1
(<)
=
c2. Then
un(O
=
&+I
(C)
&-I(<)
R%)
7
satisfies (3.12) with
p
=
n.
Additionally u-,(<)
=
-iu,(i<)
.

140
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
The first few polynomials Rn(c) defined by (3.15) are
and associated rational solutions of (3.12) are
The polynomial
&(c)
is a monic polynomial of degree in(n
+
3)
with integer coefficients. Further it has the form Rn(<)
=
Sn(c)CKn,
where
ten
=
in2
-
[l-
(-l)n]
and
Sn(C)
a monic polynomial of degree
$n
+
$[l
-
(-l)n] with simple zeros and S,(O)
#
0.
Painleve' Equations and Associated Polynomials
Poles of
us(<)
Poles of
us(<)
Poles of
245)
Poles of
u4(<)
Poles of
us(<)
-4
-3-2-10
12
3
4
Poles of
u8(<)
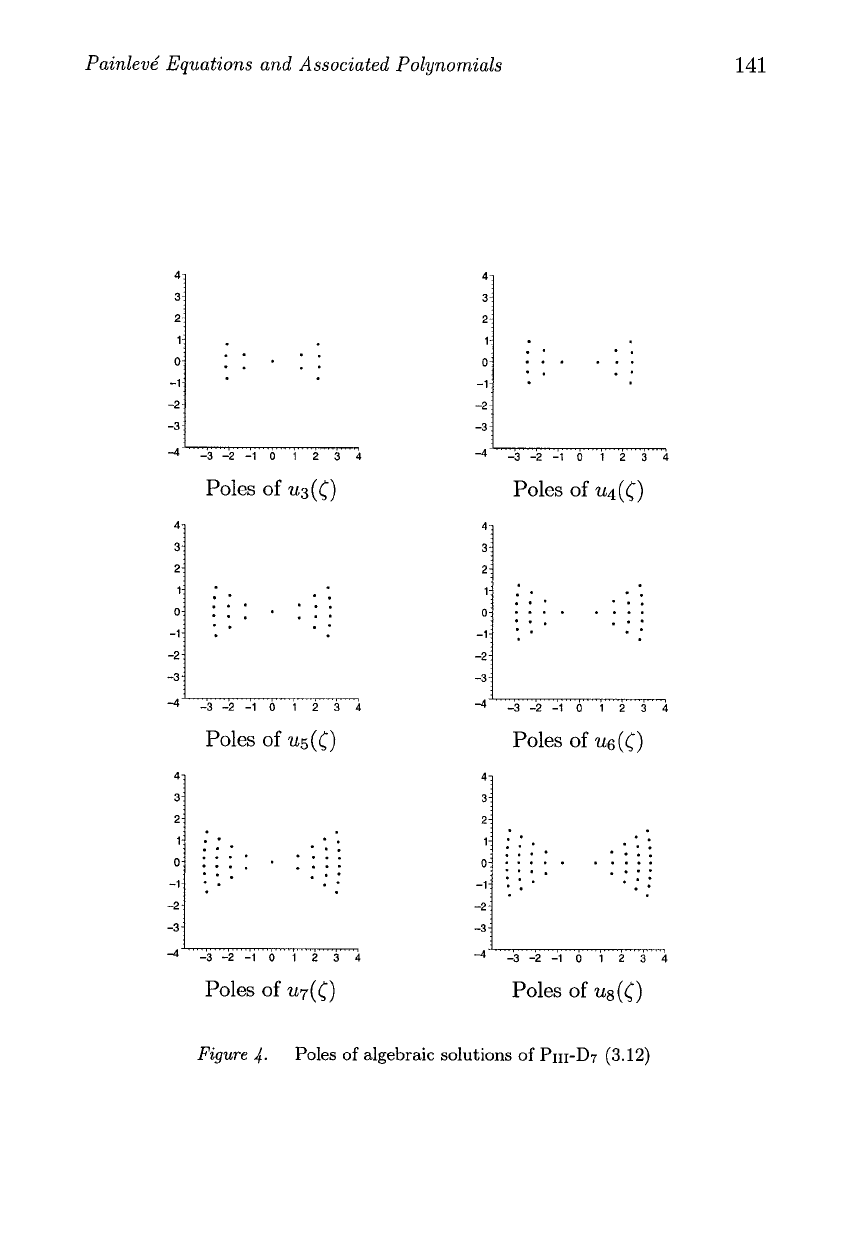
Figure
4.
Poles of algebraic solutions of
PIII-D7
(3.12)

142
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
In Figure 4 plots of the locations of the poles of the algebraic solutions
of PIII-D7 (3.12) given
by
un(z), for
n
=
3,4,
.
.
.
,8, as defined in (3.18)
are given. These take the form of two "triangles" in a "bow-tie" shape.
4.
Fourth Painlev6 equation
4.1
Rational solutions of PIv
Lukashevich (Lukashevich, 196713)) Gromak (Gromak, 1987) and Mu-
rata (Murata, 1985) (see also (Bassom et al., 1995; Gromak et al.,
2002; Umemura and Watanabe, 1997))) have proved the following theo-
rem
Theorem
4.1.
PIv
has rational solutions
if
and only
if
with
m,
n
E
Z.
Further the rational solutions for these parameter values
are unique.
Three simple rational solutions of PIv are
2
w1(2;
f
2, -2)
=
f
l/z, w2(2; 0, -2)
=
-22, w3
(2;o,
-;)
=
--
32.
(4.3)
It is known that there are three families of unique rational solutions of
PIv, which have the solutions (4.3) as the simplest members. These are
summarized in the following theorem (see (Bassom et al., 1995; Murata,
1985; Umemura and Watanabe, 1997) for further details).
Theorem
4.2.
There are three families of rational solutions of
PIv,
which have the forms

Painleve' Equations and Associated Polynomials
143
where
Pj,n(z)
and
Qj,n(2),
j
=
1,2,3,
are polynomials of degree
n,
and
The three hierarchies given in this theorem are known as the "-l/z
hierarchy", the "-22 hierarchy" and the
"-$2
hierarchy", respectively
(see (Bassom et al., 1995) where the terminology was introduced). The
"-l/z hierarchy" and the "-22 hierarchy" form the set of rational so-
lutions of
PIv
with parameter values given by (4.1) and the "-$2 hier-
archy" forms the set with parameter values given by (4.2). The rational
solutions of
PIv
with parameter values given by (4.1) lie at the vertexes
of the "Weyl chambers" and those with parameter values given by (4.2)
lie at the vertexes of the "Weyl chamber" (Umemura and Watanabe,
1997).
4.2
Okamoto polynomials
In a comprehensive study of the fourth Painlev6 equation
PIv,
Okamoto
(Okamoto, 1986), see also (Kajiwara and Ohta, 1998; Noumi and Ya-
mada, 1999; Umemura, 1998) defined two sets of polynomials analogous
to the Yablonskii-Vorob'ev polynomials associated with
PII.
These poly-
nomials are defined in Theorems 4.3 and 4.5 below, where they have been
scaled compared to Okamoto's original definition, where the polynomials
were monic, so that they are for the standard version of PIv.
Theorem
4.3.
Suppose that
Qn(z)
satisfies the recursion relation
with
Qo(z)
=
Ql (2)
=
1.
Then
W,
=
w(2;a,,Pn)
=
-
-z+
-
{ln
[Q;;;;;)]
)
,
(4.7)
3 dz
satisfies
PIv
with
(an,
,&)
=
(271,
-2).

144
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
The first few polynomials Q,(z), which are referred to as the Okamoto
polynomials, are
Remarks
4.4.
1.
The polynomials Q, (z) are polynomials of degree
n(n
-
I),
in fact
they are monic polynomials in
C
=
fiz with integer coefficients,
which is the form in which Okamoto (Okamoto, 1986) originally
defined these polynomials.
2. The hierarchy of rational solutions of
PIv
defined by (4.7) can be
derived using the following Backlund transformation of
PIv
2
(w'
-
w2
-
2zw)
+
2p
G
z;&,p
=
( -)
2w[w1-w2-2zw+2(a+l)]' (4.8)
&=a++,
p=p,
where w
r
w(z;
a,
p), which is the Backlund transformation
I+
derived by Murata (Murata, 1985) and the Schlesinger transfor-
mation
7d51
derived by Fokas, Mugan and Ablowitz (Fokas et al.,

Painleve' Equations and Associated Polynomials
1988). Specifically
where w,
=
w
(2;
2n,
-a),
with "seed solution"
wo
=
w (z; 0,
-$)
=
2
-";.
3.
The solutions w, are members of the so-called
"-$2"
hierarchy of
rational solutions of PIv, recall Theorem 4.2, which is one of three
hierarchies of rational solutions of PIv (see, for example, (Bassom
et al., 1995; Murata, 1985) for further details).
The second set of polynomials introduced by Okamoto (Okamoto,
1986) are defined in the following theorem.
Theorem
4.5.
Suppose that
S,(z)
satisfies the recursion relation
with
So(z)
=
1
and
Sl(z)
=
fiz.
Then
w
(z;
a,,
p,)
=
--z
+
-
(4.11)
3
dz
for
n
2
0,
satisfies
PIv
with
(a,,
A)
=
(2n
+
1,
-9).
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Roots of
Qg (z)
=
0
Roots of
Q6(z)
=
0
Roots of
Q4(z)
=
0
ahii
o
2-8
Roots of
Q8(z)
=
0
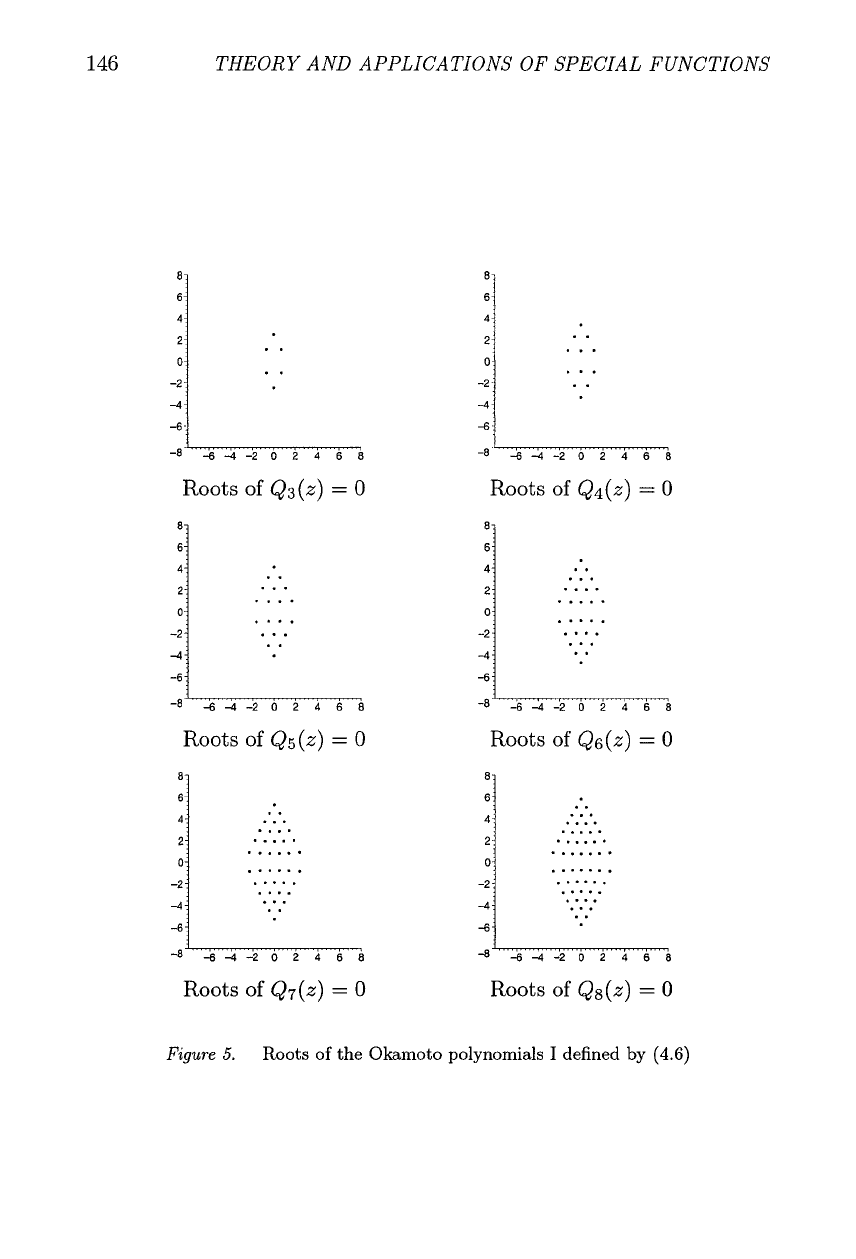
Figure
5.
bots of the Okamoto polynomials
I
defined by
(4.6)

Painleve' Equations and Associated Polynomials
The first few polynomials Sn(z), are
Remarks
4.6.
1. The polynomials Sn(z) are polynomials of degree n2, in fact they
are monic polynomials in
5
=
22 with integer coefficients, which
is the form in which Okamoto (Okamoto, 1986) originally defined
these polynomials.
2. The hierarchy of rational solutions of
PIv
defined by (4.11) can be
derived using the Backlund transformation (4.8) of PIv, derived
by Murata (Murata, 1985) and Fokas, Mugan and Ablowitz (Fokas
et al., 1988). Hence
where Gn
=
w
(z; 2n
+
1,2n
-
g),
with "seed solution"
2
Go
=
w
(z;
1,
-!)
=
-3.2
+
l/z.

148
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
3.
The solutions
67,
are also members of the so-called "-Zz" hierar-
chy of rational solutions of PIv, recall Theorem 4.2.
4. The two hierarchies of rational solutions of
PIv
given by (4.7) and
(4.11) are linked by the Schlesinger transformations and
%d31
for PIv given by Fokas, Mugan and Ablowitz (Fokas et al., 1988).
where w
=
w(z;
a,
p),
w[jl
r
w (z; abl, pb]). Specifically, for n
2
0
A
(wk
+
a)2
-
w: [8n
+
9
-
(wn
+
2~)~]
wn
=
9
(4.15)
2wn (wi
+
2zwn
-
w:,
-
a)
5. The Schlesinger transformations
R['],
R[~]
and
7?f51
are related by
R[~]R[~]
=
R[~]R[']
=
~1~1,
from the definition given by Fokas,
Mugan and Ablowitz (Fokas et al., 1988).
In Figures 5 and 6 plots of the locations of the roots for the Okamoto
polynomials Qn(z)
=
0, defined by (4.6)) and Sn(z)
=
0, defined by
(4.10)) for
n
=
3,4,.
. .
,8, respectively, are given. These both take the
form of two "triangles" with the polynomials
h(z)
having an additional
row of roots on
a
straight line between the two "triangles."
4.3
Generalized Hermite polynomials
Noumi and Yamada (Noumi and Yamada, 1999) generalized the re-
sults of Okamoto (Okamoto, 1986) and introduced the generalized Her-
mite polynomials Hm,,(z)) which are defined in Theorem 4.7 and dis-
cussed below in this section, and generalized Okamoto polynomials Qm,,(z),
