Ismail M., Koelink E. (editors) Theory and Applications of Special Functions

Подождите немного. Документ загружается.

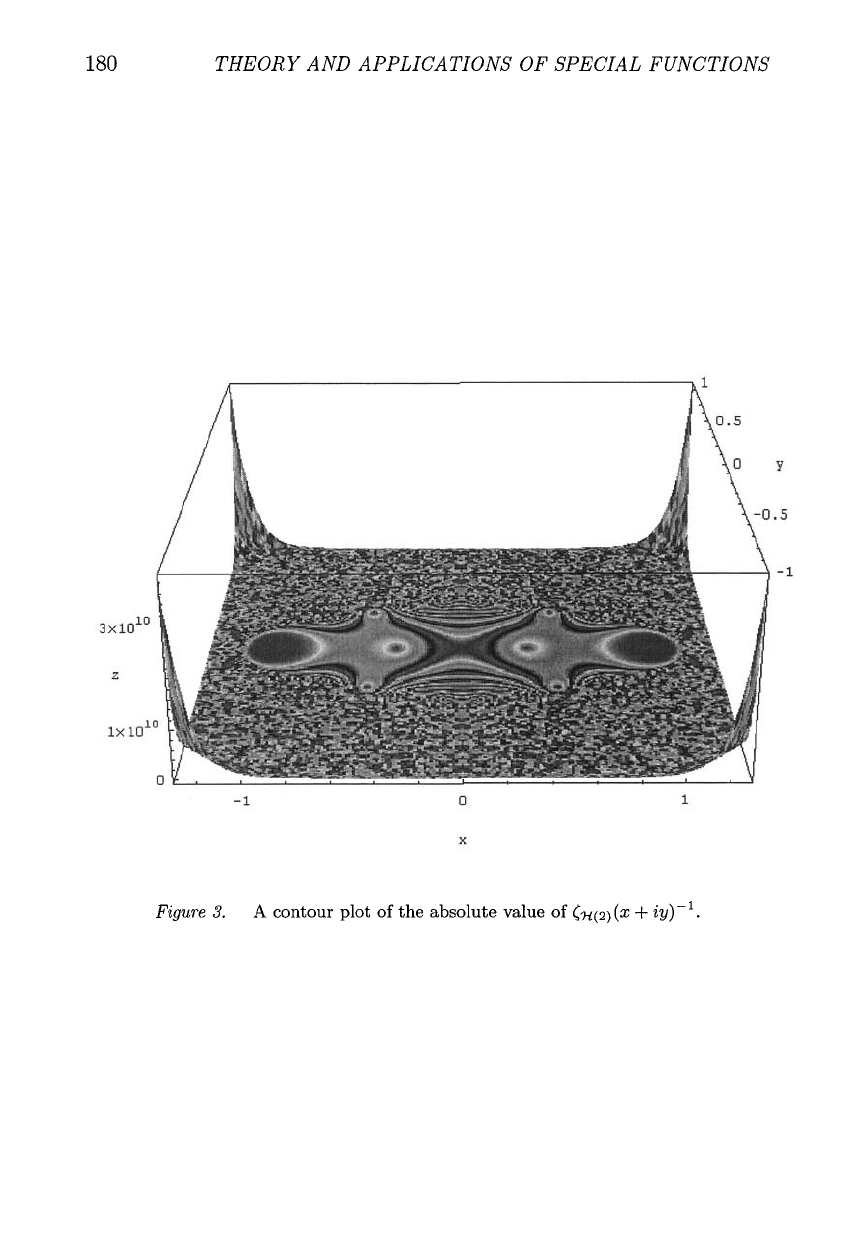
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

Figure

contour plot of the absolute value of

<x(2)(x

iy)-l.

Zeta Functions of Heisenberg Graphs over Finite Rings

181

Figure

contour plot of

1/10

power of the absolute value of

<N(4)(x

iy)-'

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

the Laplace operator on a plane drum determines the fundamental fre-

quencies of vibration). Here we wonder if one can somehow recognize

groups from properties of the zero set of zeta functions of associated

Cayley graphs with some sort of condition on the generating sets

In-

stead of hearing the drum in its spectrum, we are trying to see it. Of

course, it is known that there are graphs with the same zeta function

that are not isomorphic. See (Stark and Terras, 2000) for examples that

are connected, regular, without loops or multiple edges.

References

DeDeo, M., Martinez, M., Medrano, A., Minei, M., Stark, H., and Terras, A. (2004).

Spectra of Heisenberg graphs over finite rings. In Feng,

W.,

Hu, S., and Lin, X.,

editors, Discrete and Continuous Dynamical Systems, 2003 Supplement Volume,

pages 213-222. Proc. of 4th Internatl. Conf. on Dynamical Systems and Differential

Equations.

Diaconis, P. and Saloff-Coste,

(1994). Moderate growth and random walk on finite

groups. Geom. Funct. Anal., 4:l-36.

Godsil, C. D. (1993). Algebraic Combinatorics. Chapman and Hall, New York.

Hashimoto, K. (1990). On Zeta and L-functions of finite graphs. Intl.

Math.,

1(4):381-396.

Hofstadter, D. R. (1976). Energy levels and wave functions of Bloch electrons in

rational and irrational magnetic fields. Physical Review B, 14:2239-2249.

Katz, N. and Sarnak, P. (1999). Zeros of zeta functions and symmetry. Bull. Amer.

Math. Soc., 36(1):1-26.

Kemperman, J. H. B. (1961). The Passage Problem for a Stationary Markov Chain.

Univ. of Chicago Press, Chicago, IL.

Kotani, M. and Sunada,

(2000). Spectral geometry of crystal lattices. Preprint.

Lin, X.-S. and Wang, Z. (2001). Random walk on knot diagrams, colored Jones polyno-

mial and Ihara-Selberg zeta function. In Gillman, J., Menasco, W., and Lin, X.-S.,

editors, Knots, Braids, and Mapping Class Groups-Papers dedicated to Joan

Birman (New York, 1998), volume 24 of AMS/IP Studies in Adv. Math., pages

107-121. Amer. Math. Soc., Providence,

RI.

Lubotzky, A., Phillips, R., and Sarnak, P. (1988). Ramanujan graphs. Combinatorica,

8:261-277.

Myers, P. (1995). Euclidean and Heisenberg Graphs: Spectral Properties and Applica-

tions. PhD thesis, Univ. of California, San Diego.

Rosen, M. (2002). Number Theory in Function Fields, volume 210 of Graduate Texts

in Mathematics. Springer-Verlag, New York.

Sarnak, P. (1995). Arithmetic quantum chaos. In The Schur lectures (1992) (Tel

Aviv), volume 8 of Israel Math. Soc. Conf. Proc., pages 183-236. Bar-Ilan Univ.,

Ramat-Gan, Israel.

Stark, H. M. and Terras, A. (1996). Zeta functions of finite graphs and coverings.

Adv. in Math., 121:124-165.

Stark, H. M. and Terras, A. (2000). Zeta functions of finite graphs and coverings. 11.

Adv. in Math., 154(1):132-195.

Zeta Functions of Heisenberg Graphs over Finite Rings

183

Terras, A.

(1999).

Fourier Analysis on Finite Groups and Applications.

Cambridge

Univ. Press, Cambridge,

UK.

Terras, A.

(2000).

Statistics of graph spectra for some finite matrix groups: finite

quantum chaos. In Dunkl, C., Ismail, M., and Wong,

R.,

editors,

Special Functions

(Hong Kong,

1999), pages

351-374.

World Scientific, Singapore.

Terras, A.

(2002).

Finite quantum chaos.

Amer. Math. Monthly,

109(2):121-139.

Zack, M.

(1990).

Measuring randomness and evaluating random number generators

using the finite Heisenberg group. In

Limit Theorems in Probability and Statistics

(Pe'cs,

1989), volume

Colloq. Math. Soc. Jdnos Bolyai,

pages

537-544.

North-

Holland, Amsterdam.

Q-ANALOGUES OF SOME MULTIVARIABLE

BIORTHOGONAL POLYNOMIALS

George Gasper

Department of Mathematics

Northwestern University

Evanston,

60208

Mizan

Rahman*

School of Mathematics and Statistics

Carleton University

Ottawa, Ontario

CANADA KlS 5B6

Abstract

1989,

Tratnik found a pair of multivariable biorthogonal poly-

nomials Pn(x) and Pm(x), which is not necessarily the complex conju-

gate of Pm(x), such that

where x

(XI,.

. .

,x,),

(nl,.

,n,),

(ml,.

. .

,mp),

nj,

mj,

p,,,

is the constant of biorthogonality (which

j=1 j=1

Tratnik did not evaluate),

and the a's, blsl x's, c and

are real. In the q-case we find that the

appropriate weight function is

product of a multivariable version of

the integrand in the Askey-Roy integral and of the Askey-Wilson weight

function in a single variable that depends on XI,.

x,.

*Supported

part

the NSERC grant

#A6197.

O 2005

Springer Science+Business Media, Inc.

186

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

In a related problem we find a discrete Zvariable Racah type biorthog-

onality:

where

and

Fm,n

(x,

Y),

G,,,,,

(x, y)

are certain bivariate extensions of the

Racah polynomials.

Introduction

Wilson polynomials (Wilson, 1980), defined by

satisfy an orthogonality relation on the real line

where

is the positive weight function (under the assumption that a, b,

are

real or occur in complex conjugate pairs), and

q-Analogues of Some Multivariable Biorthogonal Polynomials

187

is the normalization constant. By Whipple's transformation it is easy to

see that Pn(x) is symmetric in a,

c, d, and that

P,(x)

b),(c

ix),(d

ix),

a),(c

ix),(d

ix),

Corresponding to each of these forms

Tratnik (Tratnik, 1989b)

introduced a multivariable polynomial:

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

where

(XI,

22,.

. .

xp),

(nl,n2,.

np),

(jl, j2,.

. .

jp),

and

and the sums in

(1.6)-(1.9)

are from

nk,

1,.

,p.

Each

of the polynomials in

(1.6)-(1.9)

is of (total) degree

in the variables

XI,

x2,

. .

x,.

The overbars in

(l.'i'),

(1.9),

and in

(1.21)

below are used

to denote distinct systems of polynomials and should not be confused

with complex conjugation. Tratnik proved that

and

q-Analogues of Some Multivariable Biorthogonal Polynomials

where

Note that in (1.12) and (1.13) the biorthogonality holds in all of the

indices nl, nz,

. . .

np, while in (1.10) and (1.11) the biorthogonality is

for polynomials of different degrees

M).

Since Whipple's

4F3

transformation does not apply for p

the P's

and Q's are no longer equivalent and hence the orthogonality in a single

variable becomes biorthogonality in many variables.

We were curious to see what their q-analogues would be. At first sight

it might appear that they could be found in a pretty straightforward

manner. We were in for a surprise. The first hurdle is an appropriate

analogue of the weight function in (1.14). There are many possible

candidates but the one that works for a q-analogue of (1.10) is:

(,&

eiek

q,6i e-iek

;

(akeiek

bke-iek; q),

P22,

k=l

where

-n

xk logq so that eiek

qixk

for

1,.

,p,

Oj,

aj,

bj,

h(cos O; c, d; q) is defined as in

j=1 j=l

(~as~er and

ahm man,

1990a, (6.1.2)))

is an arbitrary complex param-

eter such that

q*n

for n

. .

and

with

/3.

By making repeated use of the Askey-Roy integral (Gasper

and Rahman, 1990a, (4.11.1)) followed by the use of the Askey-Wilson

190

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

integral, we shall prove in Section 2 that

which is also valid for

1. It is understood that the

2)-fold

product in the numerator is taken to be

when

Let

so that

Analogous to Tratnik's polynomials in (1.6) and (1.7) we introduce the

functions