Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.

Painleve' Equations and Associated Polynomials
Roots of
Rg(z)
=
0
Roots of
R.5 (z)
=
0
Roots of
R7(z)
=
0
Roots of
R4(z)
=
0
Roots of
Rs(z)
=
0
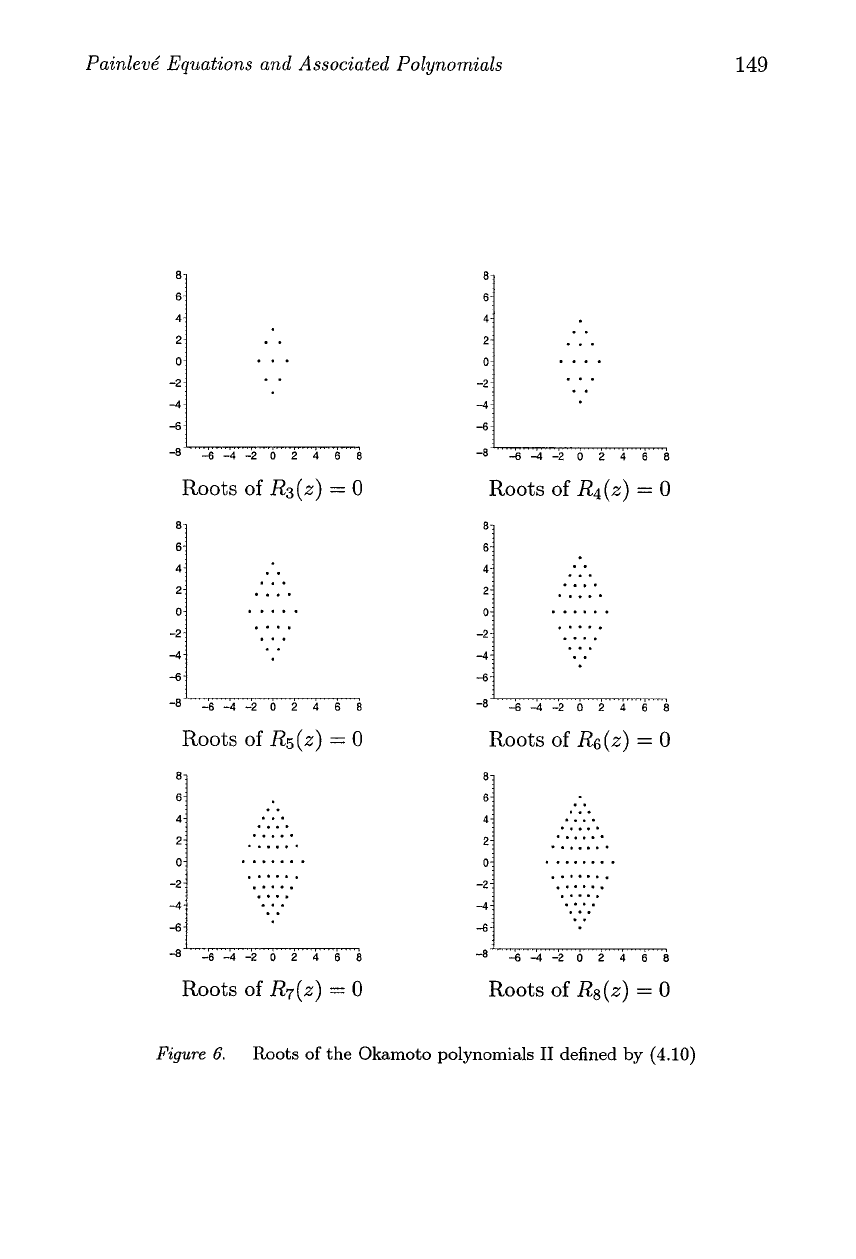
Figure
6.
Roots of the Okamoto polynomials
I1
defined by
(4.10)

150
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
which are defined in Theorem 4.9 and discussed in 54.4. Noumi and Ya-
mada (Noumi and Yamada, 1999) expressed both the generalized Her-
mite polynomials and the generalized Okamoto polynomials in terms of
Schur functions related to the so-called modified Kadomtsev-Petviashvili
(mKP) hierarchy. Kajiwara and Ohta (Kajiwara and Ohta, 1998) also
expressed rational solutions of
PIv
in terms of Schur functions by ex-
pressing the solutions in the form of determinants. Further Noumi and
Yamada (Noumi and Yamada, 1999) obtained their results on ratio-
nal solutions of PIv by considering the symmetric representation of PIv
given by the system
where p1, p2 and p3 are arbitrary constants, with pl
+
pa
+
p3
=
1,
and
the constraint
cpl+
92
+
93
=
-22. Then eliminating ~~(2) and cp3(z),
w(z)
=
cpl(z) satisfies PIV with (a, P)
=
(p3
-
pa, -2&), which was
first derived by Bureau (Bureau, 1992)
-
see also (Adler, 1994; Noumi
and Yamada, 1998a; Schiff, 1995; Veselov and Shabat, 1993).
First we discuss the generalized Hermite polynomials Hm,,(z).
Theorem
4.7.
Suppose that
Hm,,(z)
satisfies the recurrence relations
2
2mHrn+1,nHm-l7n
=
Hm,nH;,,
-
(H;,,)
+
2m~;,,,
(4.18a)
2nHm,n+lHm,n-l
=
-Hm,nH;,
+
(H;,~)~
+
2n~;,,,
(4.18b)
with
Ho,o
=
Hi,o
=
Ho,i
=
1,
H1,i
=
22,
(4.18~)
and
m, n
2
0,
then
is a solution of
PIv,
respectively for the parameters
a:!,
=
-(m
+
2n
+
1),
&),
=
-2m2,
(4.21)
a:!!
=
2m
+n
+
1,
,B:!i
=
-2n2. (4.22)

Painleve' Equations and Associated Polynomials
151
Remarks
4.8.
1. The rational solutions of PIv defined by (4.19) and (4.20) include
all the solutions in the "-l/zV and "-22" hierarchies,
as
is easily
verified by comparing the parameters in (4.21) and (4.22) with
those in (4.5a) and (4.5b).
Further they are the set of rational
solutions of
PIv
with parameter values given by (4.1).
2. Each generalized Hermite polynomial Hm,,(z) is a polynomial of
degree
mn
with integer coefficients (Noumi and Yamada, 1999).
In fact
Hmjn
($x)
is a monic polynomial in
x
of degree
mn
with
integer coefficients.
3. The polynomials H,,,(z) possess the symmetry
Hm,,(iz)
=
imn Hn,,(z), where
mn
is the degree of Hm,,(z).
4. Hn,l(z)
=
Hn(z) and H1,,(z)
=
PnHn(iz), where Hn(z) is the
usual Hermite polynomial defined by
dn
Hn
(z)
=
(-
1)" exp(z2) {exp(--z2))
.
(4.23)
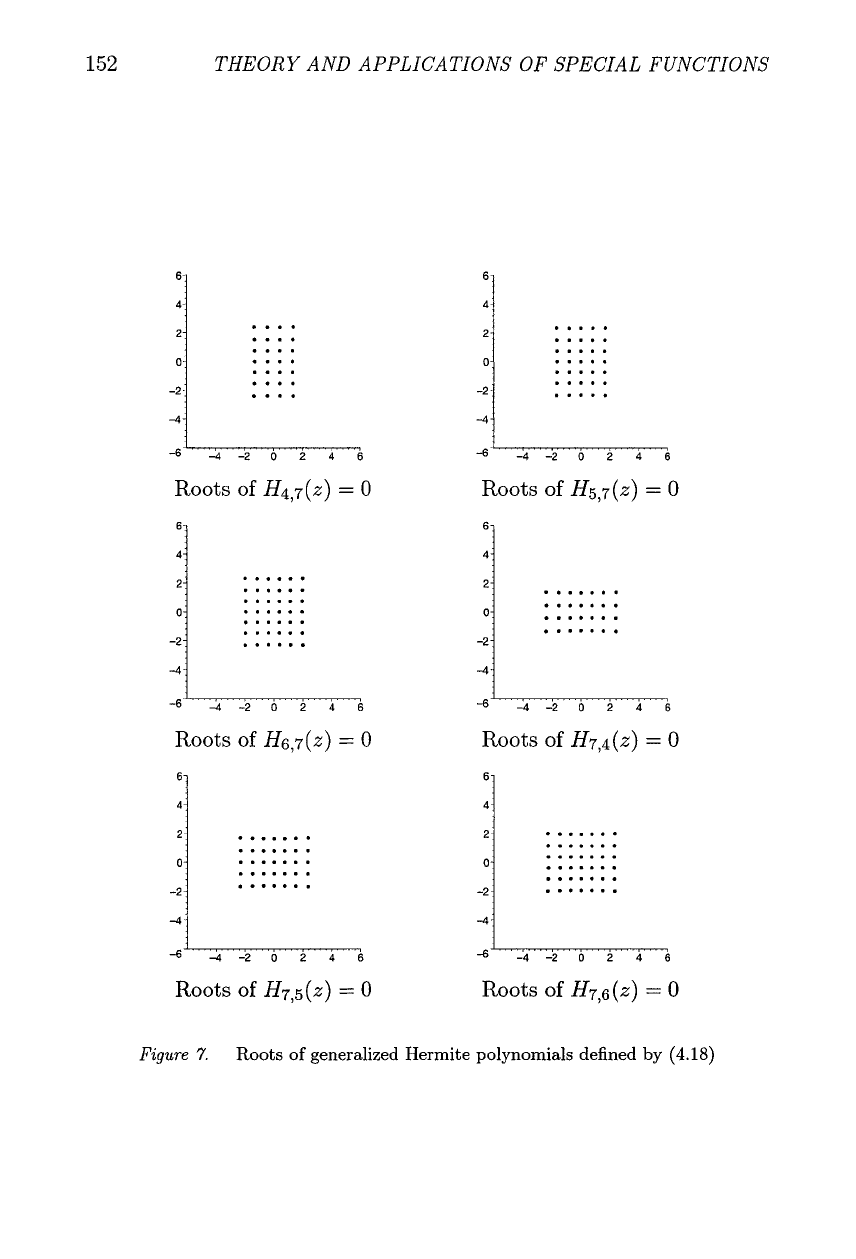
Some generalized Hermite polynomials Hm,,(z) are given in Appendix
A. Plots of the locations of the roots of the polynomials and Hm,7(z),
H7,n(z) for 4
5
m
5
6 and 4
5
n
5
6, are given in Figure
7.
These plots,
which are invariant under reflections in the real and imaginary z-axes,
take the form of
m
x
n
"rectangles", though these are only approximate
rectangles
as
can be seen by looking at the actual values of the roots.
4.4
Generalized Okamoto polynomials
In this section we discuss the generalized Okamoto polynomials Pm,,(z)
which were introduced by Noumi and Yamada (Noumi and Yamada,
1999) and are defined in Theorem 4.9 below. We have reindexed these
polynomials by setting Q,,, (z)
=
Pm-,,,
(z), i.e., Qm+,,, (z)
=
Pm,,
(z),
where Qm+n,n(z) is the polynomial defined Noumi and Yamada (Noumi
and Yamada, 1999), since we feel that Pm,,(z) is more natural, espe-
cially when one studies the plots of the locations of the roots for various
generalized Okamoto polynomials in Figure
8.
Theorem
4.9.
Suppose that Pmln(z) satisfies the recurrence relations
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Roots of
H4,7(z)
=
0
Roots of
H7,5(~)
=
0
Roots of
H5,7(z)
=
0
Roots of
H7,4(2)
=
0
Figure
7.
Roots of generalized Hermite polynomials defined by
(4.18)

Painleve' Equations and Associated Polynomials
153
with
Po,o
=
P1,o
=
Po,l
=
1,
PIJ
=
&z,
(4.24~)
then
(11)
=
2 d Pm+
1
,n
(I1)
P("))
=
--z
+
-
{ln
(-) )
,
(4.26)
n
w (2;
am,n,
m,n
3
d~
Pm,n
are solutions of
PIv,
respectively for the parameters
Remarks
4.10.
1. The rational solutions of
PIv
defined by (4.25) and (4.26) include
all the solutions in the "-$2" hierarchy,
as
is easily verified by
comparing the parameters in (4.27) and (4.28) with those in (4.5~).
Further they are the set of rational solutions of
PIv
with parameter
values given by (4.2).
2. Each polynomial Pm,,(z) is a polynomial of degree dm,,
=
m2
+
n2
+
rnn
-
m
-
n
with integer coefficients (Noumi and Yamada,
1999). Further Pm,,(z) is a monic polynomial in
<
=
&
z of degree
dm,, with integer coefficients.
3. The original Okamoto polynomials defined in Theorems 4.3 and 4.5
are respectively given by Qm(z)
=
Pmlo(z) and &(z)
=
Pm,l
(2).
4. The polynomials
Pmln(2)
possess the symmetry
Pm,n(iz)
=
exp($ridm,,) Pn,m(z), where dm,,
=
m2
+
n2
+
mn
-
m
-
n
is the degree of Pm,,(z).
5. The hierarchies of rational solutions of
PIv
generated from the gen-
eralized Hermite polynomials Hm,n(z) defined in Theorem 4.7 and
the generalized Okamoto polynomials Pmln(z) defined in Theorem
4.9 are linked by the Schlesinger transformations
%d2]
(or
7d41)
and
R[~]
z
R[']R[~]
given by Fokas, Mugan and Ablowitz (Fokas et al.,
1988).
Some generalized Okamoto polynomials Pm,,(z) are given in Ap-
pendix
B.
Plots of the locations of the roots of the polynomials and
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Roots of
P4,7(z)
=
0
Roots of
P5,7(z)
=
0
Roots of
P6,7(z)
=
0
Roots of
P74(z)
=
0
Roots of
P7,5(~)
=
0
Roots of
P7,6(~)
=
0
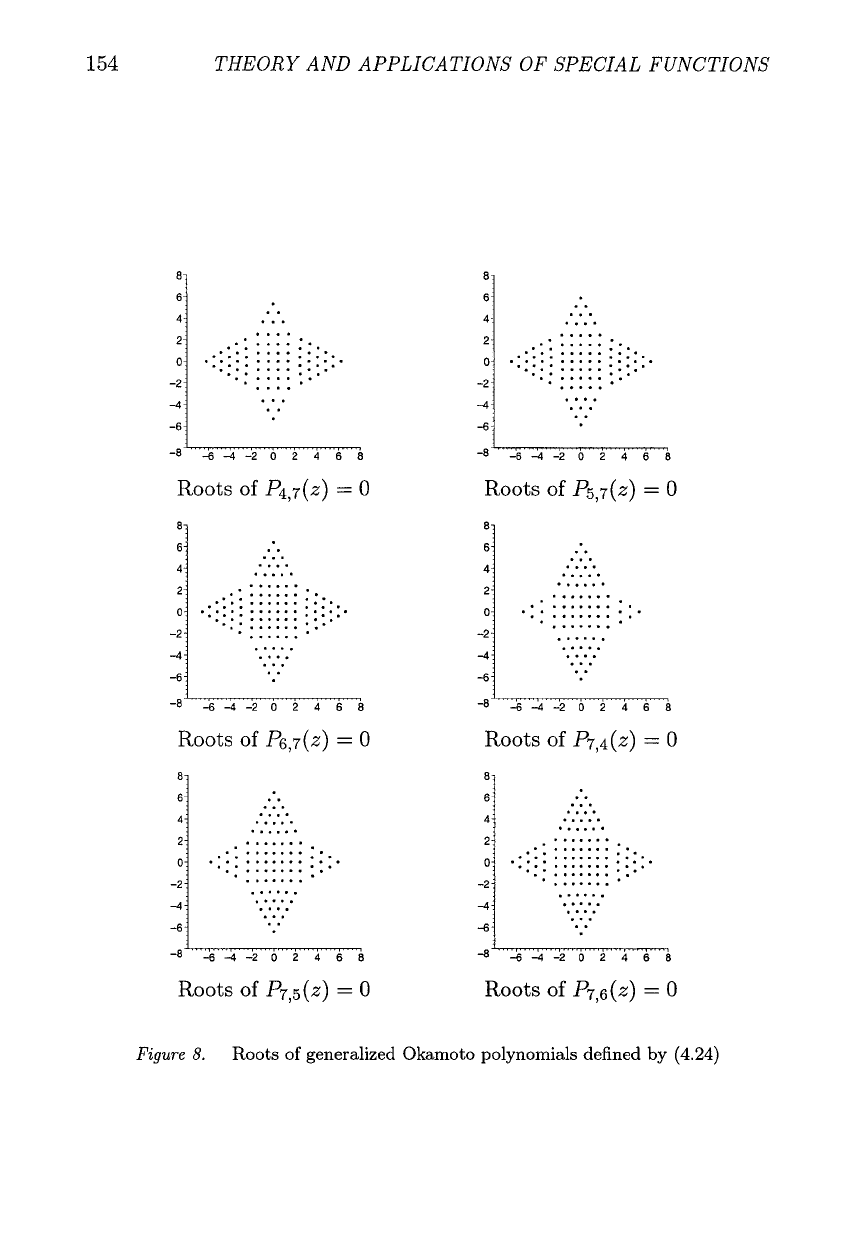
Figure
8.
Roots of generalized Okamoto polynomials defined by
(4.24)

Painleve' Equations and Associated Polynomials
155
Pm,7(~), P~,,(z) for 4
5
m
5
6 and
4
5
n
5
6,
are given in Figure
8.
The roots of the polynomial Pm,,(z) takes the form of
m
x
n
"rectangles"
with an "equilateral triangle," which have either
m
-
1
or
n
-
1
roots on
each of its sides. These are only approximate rectangles and equilateral
triangles as can be seen by looking at the actual values of the roots. The
triangles We remark that as for the Bi-Hermite polynomials above, the
plots are invariant under reflections in the real and imaginary z-axes.
5.
Conclusions
An important, well-known property of classical orthogonal polynomi-
als, such as the Hermite, Laguerre or Legendre polynomials whose roots
all lie on the real line (cf. (Abramowitz and Stegun, 1972; Andrews et al.,
1999; Temme, 1996)), is that the roots of successive polynomials inter-
lace. Thus for a set of orthogonal polynomials p,(z), for
n
=
0,1,2,.
. .
,
if znlm and z,,,+l are two successive roots of p,(z), i.e.,
p,
(z,,,)
=
0
and pn (zn,m+l)
=
0, then
9,-1
(<,-I)
=
0
and pn+l (&+I)
=
0
for some
and such that
zn,,
<
<,+i
<
zn,,+l. Further the deriva-
tives pL(z) and ~;+~(z) also have roots in the interval (zn,m,zn,m+l),
that is
pL
(tn)
=
0 and
pL+l
(en+l)
=
0
for some
en
and such that
zn,m
<
tn,
tn+l
<
zn,m+l-
An interesting open question is whether there are analogous results
for the polynomials associated with rational and algebraic solutions of
the Painlev6 equations discussed here. Clearly there are notable differ-
ences since these special polynomials have complex roots whereas clas-
sical orthogonal polynomials p,(~), have real roots. The pattern of the
roots of the special polynomials associated with the Painlev6 equations
are highly symmetric and structured, suggesting that they have inter-
esting properties. A particularly interesting question is whether there
is any "interlacing of roots" analogous to that for classical orthogonal
polynomials. Clearly this warrants further analytical study as does an
investigation of the relative locations of the roots for the special polyno-
mials and their derivatives. We shall not pursue these questions further
here.
Acknowledgments
I wish to thank Mark Ablowitz, Frederick Cheyzak, Chris Cosgrove,
Andy Hone, Nalini Joshi, Arieh Iserles, Alexander Its, Elizabeth Mans-
field and Marta Mazzocco for their helpful comments and illuminating
discussions. This research arose whilst involved with the "Digital Library
of Mathematical Functions" project (see
http:
//dlmf
.nist
.gov/),
in

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
particular
I
thank Frank Olver and Dan Lozier for the opportunity to
participate in this project.
References
Ablowitz, M.
J.
and Clarkson, P. A.
(1991).
Solitons, Nonlinear Evolution Equations
and Inverse Scattering, volume
149
of Lecture Notes in Mathematics. Cambridge
University Press, Cambridge.
Ablowitz, M.
J.
and Satsuma,
J.
(1978).
Solitons and rational solutions of nonlinear
evolution equations.
J.
Math. Phys.,
19:2180-2186.
Abramowitz, M. and Stegun, I. A.
(1972).
Handbook of Mathematical Functions.
Dover, New York, tenth edition.
Adler,
M.
and Moser,
J.
(1978).
On a class of polynomials associated with the
Korteweg-de Vries equation. Commun. Math. Phys.,
61:l-30.
Adler, V.
E.
(1994).
Nonlinear chains and Painlev6 equations. Physica,
D73:335-351.
Airault, H.
(1979).
Rational solutions of Painlev6 equations. Stud. Appl. Math.,
61:31-
53.
Airault, H., McKean,
H.
P.,
and
Moser,
J.
(1977).
Rational and elliptic solutions of
the KdV equation and related many-body problems. Commun. Pure Appl. Math.,
30:95-148.
Albrecht, D.
W.,
Mansfield,
E.
L., and Milne, A.
E.
(1996).
Algorithms for special
integrals of ordinary differential equations.
J.
Phys. A: Math. Gen.,
29:973-991.
Andrews,
G.,
Askey, R., and Roy,
R.
(1999).
Special Functions, volume
71
of Ency-
clopedia of Mathematics and its Applications. Cambridge University Press, Cam-
bridge.
Bassom, A. P., Clarkson, P.
A.,
and Hicks, A. C.
(1995).
Backlund transformations
and solution hierarchies for the fourth Painlevk equation. Stud. Appl. Math.,
95:l-
71.
Bureau, F.
(1992).
Differential equations with fixed critical points. In Painleve' tran-
scendent~ (Sainte-AdBle, PQ, 1990), volume
278
of NATO Adv. Sci. Inst. Ser.
B
Phys., pages
103-123.
Plenum, New York.
Charles, P.
J.
(2002).
Painleve' analysis and the study of continuous and discrete
Painleve' equations. PhD thesis, Institute of Mathematics and Statistics, University
of Kent, UK.
Clarkson, P. A. and Kruskal, M. D.
(1989).
New similarity solutions of the Boussinesq
equation.
J.
Math. Phys.,
30:2201-2213.
Clarkson, P. A. and Mansfield,
E.
L.
(2003).
The second Painlev6 equation, its hier-
archy and associated special polynomials. Nonlinearity,
16:Rl-R26.
Flaschka, H. and Newell, A. C.
(1980).
Monodromy-and spectrum preserving defor-
mations.
I.
Commun. Math. Phys.,
76:65-116.
Fokas, A. S. and Ablowitz, M.
J.
(1982).
On a unified approach to transformations
and elementary solutions of Painlev6 equations.
J.
Math. Phys.,
23:2033-2042.
Fokas, A. S., Mugan, U., and Ablowitz, M.
J.
(1988).
A method of linearisation for
Painlev6 equations: Painlevk IV, V. Physica,
D30:247-283.
Fokas, A. S. and Yortsos, Y. C.
(1981).
The transformation properties of the sixth
painlev6 equation and one-parameter families of solutions. Lett. Nuovo Cim.,
30:539-
544.

Painleve' Equations and Associated Polynomials
157
Fukutani, S., Okarnoto, K., and Umemura, H. (2000). Special polynomials and the
Hirota bilinear relations of the second and fourth Painlevk equations. Nagoya Math.
J., 159:179-200.
Gambier, B. (1910). Sur les kquations diffkrentielles du second ordre et du premeir
degre dont l'intkgrale gknkrale est
B
points critiques fixks. Acta Math., 33:l-55.
Gromak,
V.
I.
(1973). The solutions of Painlevk's third equation. Diff. Eqns., 9:1599-
1600.
Gromak, V.
I.
(1975). Theory of Painlevk's equation. Diff. Eqns., 11:285-287.
Gromak, V.
I.
(1976). Solutions of Painlevk's fifth equation. Diff. Eqns., 12:519-521.
Gromak, V.
I.
(1978a). Algebraic solutions of the third Painlevk equation. Dokl. Akad.
Nauk BSSR, 23:499-502.
Gromak, V.
I.
(197813). One-parameter systems of solutions of Painlevk's equations.
Diff. Eqns., 14:1510-1513.
Gromak, V.
I.
(1987). Theory of the fourth painlevk equation. Diff. Eqns., 23:506-513.
Gromak, V.
I.
(1999). Backlund transformations of Painlevk equations and their ap-
plications.
In
Conte, R., editor, The Painlevk Property, One Century Later, CRM
Series in Mathematical Physics, pages 687-734. Springer, New York.
Gromak, V.
I.
(2001). Backlund transformations of the higher order Painlevk equa-
tions. In Coley, A., Levi,
D.,
Milson, R., Rogers, C., and Winternitz, P., editors,
Backlund and Darboux transformations. The geometry of solitons (Halifax, NS,
1999), volume 29 of CRM Proc. Lecture Notes, pages 3-28. Amer. Math. Soc.,
Providence, RI.
Gromak, V.
I.,
Laine,
I.,
and Shimomura, S. (2002). Painlevk Differential Equations
in
the Complex Plane, volume 28 of Studies in Mathematics. de Gruyter, Berlin,
New York.
Gromak,
V.
I.
and Lukashevich, N.
A.
(1982). Special classes of solutions of Painlevk's
equations. Diff. Eqns., 18:317-326.
Iwasaki, K., Kajiwara, K., and Nakamura, T. (2002). Generating function associated
with the rational solutions of the Painlevk I1 equation. J. Phys. A: Math. Gen.,
35:L207-L211.
Iwasaki, K., Kimura, H., Shimomura, S., and Yoshida, M. (1991). From Gauss to
Painlevk: a Modern Theory of Special Functions, volume 16 of Aspects of Mathe-
matics E. Viewag, Braunschweig, Germany.
Jimbo, M. and Miwa, T. (1983). Solitons and infinite dimensional Lie algebras. Publ.
RIMS, Kyoto Univ., 19:943-1001.
Kajiwara, K. and Masuda,
T.
(1999a). A generalization of determinant formulae
for the solutions of Painlevk I1 and XXXIV equations.
J.
Phys. A: Math. Gen.,
32:3763-3778.
Kajiwara, K. and Masuda, T. (1999b). On the Umemura polynomials for the Painlevk
I11 equation. Phys. Lett., A260:462-467.
Kajiwara, K. and Ohta,
Y.
(1996). Determinantal structure of the rational solutions
for the painlevk I1 equation. J. Math. Phys., 37:4393-4704.
Kajiwara, K. and Ohta,
Y.
(1998). Determinant structure of the rational solutions for
the Painlevk
IV
equation.
J.
Phys. A: Math. Gen., 31:2431-2446.
Kametaka,
Y.
(1983). On poles of the rational solution of the Toda equation of
PainlevbII type. Proc. Japan Acad. Ser. A Math. Sci., 59:358-360.

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Kametaka, Y. (1985). On the irreducibility conjecture based on computer calculation
for YablonskiY-Vorobev polynomials which give a rational solution of the Toda
equation of Painlev6-11 type. Japan
J.
Appl. Math., 2:241-246.
Kaneko, M. and Ochiai, H. (2002). On coefficients of Yablonskii-Vorob'ev polynomi-
als. Preprint, arXiv:math.QA/0205178.
Kirillov, A. N. and Taneda, M. (2002a). Generalized Umemura polynomials. Rocky
Mount.
J.
Math., 32:691-702.
Kirillov, A.
N.
and Taneda, M. (2002b). Generalized Umemura polynomials and
Hirota-Miwa equations. In Kashiwara, M. and Miwa, T., editors, MathPhys Odyssey,
2001,
volume 23 of Prog. Math. Phys., pages 313-331. Birkhauser-Boston, Boston,
MA.
Lukashevich, N. A. (1965). Elementary solutions of certain Painlev6 equations. Diff.
Eqns., 1:561-564.
Lukashevich, N. A. (1967a). On the theory of the third Painlev6 equation. Diff. Eqns.,
3:994-999.
Lukashevich, N. A. (196713). Theory of the fourth Painlev6 equation. Diff. Eqns.,
3:395-399.
Lukashevich, N. A. (1968). Solutions of the fifth equation of painlev6 equation. Diff.
Eqns., 4:732-735.
Lukashevich, N. A. (1971). The second painlevk equation. Diff. Eqns., 6:853-854.
Lukashevich, N. A. and Yablonskii, A. I. (1967). On
a
class of solutions of the sixth
painlevk equation. Diff. Eqns., 3:264-266.
Masuda, T. (2002). On a class of algebraic solutions to Painlev6 VI equation, its
determinant formula and coalescence cascade. preprint, arXiv:nlin.S1/0202044.
Masuda,
T.,
Ohta, Y., and Kajiwara, K. (2002). A determinant formula for a class of
rational solutions of Painlev6 V equation. Nagoya Math. J., 168:l-25.
Mazzocco, M. (2001). Rational solutions of the Painlev6 VI equation.
J.
Phys. A:
Math. Gen., 34:2281-2294.
Milne, A. E., Clarkson, P. A., and Bassom, A. P. (1997). Backlund transformations
and solution hierarchies for the third Painlev6 equation. Stud. Appl. Math., 98:139-
194.
Murata, Y. (1985). Rational solutions of the second and the fourth Painlev6 equations.
Funkcial. Ekvac., 28:l-32.
Murata, Y. (1995). Classical solutions of the third Painlev6 equations. Nagoya Math.
J., 139:37-65.
Noumi, M. and Yamada, Y. (1998a). Affine Weyl groups, discrete dynamical systems
and Painlev6 equations. Commun. Math. Phys., 199:281-295.
Noumi, M. and Yamada, Y. (1998b). Umemura polynomials for the Painlev6 V equa-
tion. Phys. Lett., A247:65-69.
Noumi, M. and Yamada, Y. (1999). Symmetries in the fourth Painlev6 equation and
Okamoto polynomials. Nagoya Math.
J.,
153:53-86.
Noumi M., Okada
S.,
0.
K. and H.,
U.
(1998). Special polynomials msociated with
the Painlev6 equations. 11. In Saito, M.-H., Shimizu, Y., and Ueno,
R.,
editors,
Integrable Systems and Algebraic Geometry, pages 349-372. World Scientific, Sin-
gapore.
Ohyama, Y. (2001). On the third Painlev6 equations of type
d7.
Preprint, Department
of Pure and Applied Mathematics, Graduate School of Information Science and
Technology, Osaka University.
