Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.


444
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Theorem
1.1.
Let E, be an ellipse
in
the complex x-plane
with the semiaxes given by
and the focal points at
f
1; let
Int
EE be the interior of the ellipse E, and
Ext
EE be the exterior of E,. Suppose that a sequence of polynomials
{P~(X))~=~~
deg
pn(x)
=
n, n
=
0,1,2,
. . .
,
such that all zeros of pn(x)
lie in the interval (-1, I), satisfies the following inequalities
where C1(&)
>
0, on the ellipse E, with 0
<
q
<
1,
E
>
0 for all
suficiently large
n.
Then the series (1.1) converges absolutely for every
x
in the interior of the ellipse E,
:
with
l/n
qE
=
lim sup
1
cn
1
.
n--tea
If 0
<
E'
<
E,
the convergence is uniform
in
the closure of the interior of
the subellipse EE,. For every x in the interior of the ellipse E, the sum
of the series (1.1) is an analytic function. For every x in the exterior of
the ellipse EE the terms of the series (1.1) are unbounded, and the series
is consequently divergent.
We shall call the ellipse
EE
given
by (1.2)-(1.3)
and
(1.6)
the
ellipse
of convergence;
nothing is claimed about the convergence on the ellipse.
The proof of Theorem
1.1
here is similar to the proof of Theorem
6.12
in (Suslov,
2003b);
see also Exercise
6.21.
Proof.
Let
EE be
the ellipse of convergence given above. When
0
<
6
<
E
and
qE
<
q"-S,
by
the definition of limit superior there exists an
no
>
0
such that
~~l~/~<~~-~,
or
l~l<~('-*)~
(1.7)
for all
n
>
no.
If
0
<
E'
<
E,
the following estimate holds

Expansions in q-Polynomials 445
for all
n
>
no
and every
x
inside the ellipse
EEl
due to the maximum
principle for the analytic functions and the hypotheses of the theorem.
Thus, when
E'
<
E
-
6, 0
<
6
<
E,
for large
n
the series
(1.1)
has a
convergent geometric series
as
a majorant, and consequently converges
absolutely.
For every
x
on the subellipse
E,I,
0
<
E'
<
E
and in its
interior Int
Eel
the convergence is uniform by the M-test and, therefore,
by the Weierstrass theorem the limit function is analytic inside
EE.
If
E'
>
E
>
0, we choose 6, 0
<
6
<
E'
-
E
SO
that
q"'
<
qE+b
<
qE.
Since
qE+6
<
qE
there are arbitrary large
n
such that
Thus
when
x
E
EE1
c
Ext
EE,
for infinitely many
n,
and the terms are un-
bounded. This completes the proof of the theorem.
0
Remark
1.2.
If under the hypotheses of Theorem 1.1 the set of poly-
nomials {pn (x)}:=~, instead of satisfying the inequalities (1.4), is uni-
formly bounded on compacts
1
P~(x)
I
<
D
=
constant
(1.11)
for all suficiently large
n
and
then the series (1.1) is an entire function
in
the complex x-plane.
Remark
1.3.
It follows from the second part of the proof of Theorem
1.1 that the imposed condition that all zeros of pn(x) lie
in
the interval
(-1,l) can be replaced by weaker requirements that those zeros lie inside
the ellipse of convergence and the lower bound
in
(1.4) holds only outside
the ellipse of convergence. The Cauchy-Hadamard formula holds also
in
the case of Szegii's class of orthogonal polynomials (Szegii, 1975),
Theorems 12.7.3-12.7.4 and (Szeg6, 1982, p.
377),
but our approach
does not require orthogonality; see (Suslov, 2003a) for more details.
Remark
1.4.
Theorem 1.1 holds also for a sequence of analytic func-
tions {fn(x)}
if
the conditions (1.4) are satisfied. By the Root Test the
l/n
theorem holds also under conditions
lim
c~/~(E)
=
lim
C2
(E)
=
1;
n+m
n+oa
cf. (Davis, 1963, Lemma 4.4.2, p. 89).

446
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
2.
Some Expansions in Classical q-Orthogonal
Polynomials
Let us consider the maximum domain of analyticity for several familiar
expansions in q-orthogonal polynomials.
2.1
The continuous q-ultraspherical polynomials
These polynomials are defined by
where x
=
cos8; see, for example, (Andrews et al., 1999) and (Gasper
and Rahman, 1990); we shall assume throughout the paper that
-1
<
,B
<
1
and 0
<
q
<
1.
Let us establish first a convenient upper bound.
Lemma
2.1.
The following inequalities hold
for
E
>
0,
-1
<
p
<
1
and
0
<
q
<
1
when x is inside or on the ellipse
E,
given
by
(1.2)-(1.3).
Proof. As in the proof of Lemma
6.8 in (Suslov, 2003b), we rewrite the
relation (2.1) in the form
Let
z
=
Re
z
+
i
Im
z
with Re z
=
E',
qi
ImZ
=
eie, or qZ
=
eieq"', where
0
5
E'
5
E. Then
1
x
=
1
(6'
+
q-s')
cos
e
+
i-
(qc'
-
q-~') sin
e
2
2
and the image of the vertical line segment given by Re z
=
E',
Im z
=
8 log q,
-.rr
5
0
5
.rr
is the ellipse
E,I
in the complex x-plane; see Figure
1.
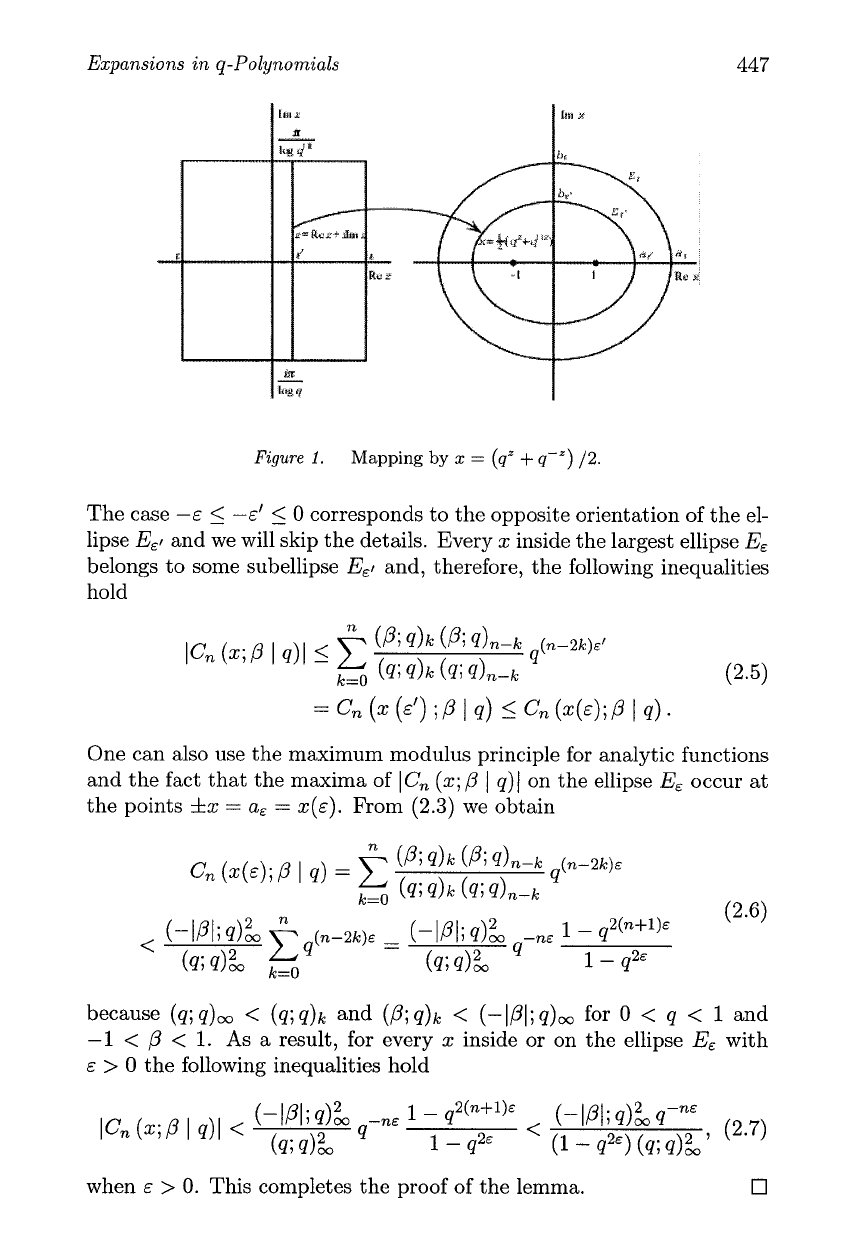
Expansions in q-Polynomials
Figure
I.
Mapping
by
x
=
(qZ
+
q-')
12.
The case
-E
5
-E'
5
0
corresponds to the opposite orientation of the el-
lipse
E,t
and we will skip the details. Every x inside the largest ellipse
E,
belongs to some subellipse
Eel
and, therefore, the following inequalities
hold
One can also use the maximum modulus principle for analytic functions
and the fact that the maxima of
ICn
(x;
,6
I
q)l on the ellipse
E,
occur at
the points
f
x
=
a,
=
x(E).
From (2.3) we obtain
because (%!I),
<
(%q)k and (P;q)k
<
(-1Pl;q)co for
0
<
4
<
1 and
-1
<
p
<
1. As a result, for every x inside or on the ellipse
EE
with
E
>
0
the following inequalities hold
when
E
>
0.
This completes the proof of the lemma.
0

448
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
We need to show that the hypotheses of Theorem
1.1
are satisfied
for the continuous q-ultraspherical polynomials. This can be done with
the help of the uniform asymptopic for these polynomials which one can
establish with the help of the following result (Bromwich, 1965), (Ismail
and Wilson, 1982).
Theorem
2.2
(Tannery's theorem).
Let
m
Sn
=
a0
(n)
+
a1
(n)
+
. .
+
a,
(n)
=
x
ar. (n)
;
(2.8)
k=O
lim ak (n)
=
bk,
Ic
being fixed;
n+m
(2.9)
and
lak(n)l5Mk,
C~k<m,
(2.10)
k
where
Mk
is independent
of
n. Then
lim
Sn
=
bk,
n+m
it is being understood that
m
=
m
(n)
+
m as n
+
m.
See (Bromwich, 1965) for the proof of this theorem; the result holds
uniformly with respect to all parameters in compact sets if the conver-
gence in (2.9) and bound in (2.10) hold uniformly.
In the case of the continuous q-ultraspherical polynomials
Eq.
(2.3)
implies that
where
with
-1
<
p<
1,
0
<
q
<
1
and
Also
lim
(Pi
q)n-k
(P;
q)k
2kz
((P; q)m (P; q)k q2kz
4
-
n'w
(4; q)n-k (4; 4)k
(4; q)m (4;
dk

Expansions in q-Polynomials 449
Thus by the Tannery theorem
2kr
((P;
q)m (Pq2"; q),
lim
qn"Cn
(x;
P
1
9)
=
n+co
4
-
(4;
dm
(q2"; 41,
due to the q-binomial theorem.
One can easily see that the resulting limiting relation
lim
qnzCn (x;
p
1
q)
=
(P,
Pq2";
P)
,
n+m
14"1
<
1 (2.16)
(4, q2";
d,
holds uniformly on the ellipse
EE
with
x
=
(qZ
+
q-") 12
and
q"
=
q"eie,
E
>
0.
Indeed, the bound in
(2.13)
is uniform on
EE
and the convergence in
(2.9)
holds uniformly due to Cauchy's criteria. It is clear that
is arbitrary small on the ellipse for all sufficiently large
m
and
n.
Now we can show that the conditions
(1.4)
of Theorem
1.1
are satis-
fied.
Lemma
2.3.
The following inequalities hold
for
E
>
0,
-1
<
p
<
1
and
0
<
q
<
1 for all suficiently large
n
and
every
x
on the ellipse
E,
given by (1.2)-(1.3).
Proof.
Let
x(z)
=
(qZ
+
q-") 12
and
q"
=
eieq'
with
E
>
0,
-T
5
0
5
n.
In view of
(2.16),
uniformly on the ellipse
E,.
This means that for a given
€0
>
0 there is
no
=
no
(E~)
such that

450
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
for all n
2
no and x
E
EE.
Introducing
LI
=
min
L
(B),
L2
=
max
L
(B),
01e5~l2
o<e<~/a
(2.20)
one can write
for all n
2
no and x
E
EE.
Choosing
we arrive at inequalities (2.17) uniformly on the ellipse
EE
and the proof
is complete.
0
As the first example, let us consider convergence of the series in the
Ismail and Zhang formula (Ismail and Zhang, 1994),
8,
(x;
iw)
=
(Q;
q)oo~-~
(qv;
dm
(-qw2; q2)00
00
(2.23)
4
(2)
x
C
"
(1
-
qVf
")
qn
'
Jv+n (2~; q) Cn
(2;
qV
I
q)
where
J$~
(2w; q) is Jackson's q-Bessel function defined by
with
v
>
-1
and the basic exponential function on a q-quadratic grid is
given by
with
x
=
cosB and
Ial
<
1.
This function was originally introduced by
Ismail and Zhang (Ismail and Zhang, 1994) with different notation and
normalization; see also (Atakishiyev and Suslov, 1992), (Suslov, 1997)
for the corresponding solutions of a q-analog of the equation for harmonic
motion; the above notation is due to Suslov (Suslov, 1997). Different
proofs of the Ismail and Zhang formula were given in (Floreanini and

Expansions in q-Polynomials 451
Vinet, 1995), (Ismail et al., 1999)) (Ismail et al., 1996), and (Ismail and
Stanton, 2000); see also (Suslov, 2003b), Section 4.5.
From (2.24) we obtain
by the Jacobi triple product identity (Andrews et al., 1999), (Gasper
and Rahman, 1990). This upper bound is of an independent interest.
Introducing
in view of (2.26) one gets
with
D
=
(-%
dm
(-p1+vlw12,
-q'+'/l~1~; q2),.
(2.29)
(a;
a)co
Therefore
and
qC=limsup~Gllln=O, or
E=W.
(2.31)
n-+w
The series in (2.23) is an entire function in the complex x-plane for all
finite values of
w,
thus providing an analytic continuation of the basic
exponential function (2.25).
In a similar fashion, one can show that the ellipse of convergence of the
series in Rogers' generating function for the continuous q-ultraspherical
polynomials,
a
(@reie, @re-ie
;
q)
,
CC,(COS~;~
I
q)rn
=
,
Irl
<
1
(2.32)
(reie, re-ie; q),
n=O
see, for example, (Andrews et al., 1999) and (Gasper and Rahman,
1990), is the ellipse
E,
given by (1.2)-(1.3) with

452
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Observe that the first poles in the right side of (2.32) are located on
the ellipse of convergence. In a similar manner, one can analyze the
convergence of the series in the Poisson kernel for the continuous q-
ultraspherical polynomials and in related bilinear generating functions
(Gasper and Rahman, 1990).
2.2
The continuous q-Hermite polynomials
These polynomials are the special case of the continuous q-ultraspherical
polynomials:
Hn
(X
1
4)
=
(4; q)nCn (2; 0
I
q)
.
(2.34)
They have two generating functions
and
see, for example, (Suslov, 2003b) and (Gasper and Rahman, 1990), re-
spectively.
By Lemma 2.1 and (2.34) the uniform upper bound is
and in the first case (2.35)) the series defines an entire function in the
complex x-plane for all finite values of
a.
Indeed,
In the second case (2.36), by Lemma 2.3 and (2.34) the corresponding
ellipse of convergence
EE
is given by (1.2)-(1.3) with
qE
=
lim sup (1rln)'ln
=
n--100
Irl.
The first poles in the right side of (2.36) occur on the ellipse of conver-
gence.
Ismail and Stanton (Ismail and Stanton, 2000) have found the follow-
ing expansion formula

Expansions in q-Polynomials 453
in the continuous q-Hermite polynomials.
They call expansion (2.38)
the "addition" theorem with respect to the parameter
a
because it be-
comes exp ax exp px
=
exp
(a
+
p) x in the limit q
--+
I-; see (Suslov,
1997), (Suslov, 2000) and (Suslov, 2003b, Chapter 3), for other addition
theorems for the basic exponential functions.
One can easily verify with the help of (1.8) of (Gasper and Rahman,
1990) that
when
n
=
2k and
when
n
=
2k
+
1. Thus, the corresponding ellipse of convergence is
Em
and the series represents an entire function.
2.3
The Askey-Wilson polynomials
These polynomials are given by
=
awn (ab, ac, ad; q),
493
q-n, abcdqn-l, aeie,
ab, ac, ad
where x
=
cos
6.
They are the most general known classical orthogonal
polynomials; see, for example, (Andrews and Askey, 1985), (Askey and
Wilson, 1985)) and (Gasper and Rahman, 1990).
The uniform asymptotic on the ellipse
E,,
namely,
when max (la[,
Ibl,
IcI,
[dl)
<
1
and IqZ
I
<
1,
was established in (Ismail
and Wilson, 1982) with the help of the Tannery theorem; see also (Rah-
man, 1986) and (Gasper and Rahman, 1990) for another approach. The
